Algorithmic Analysis of Chemical Dynamics of the Autoignition of NH3–H2O2/Air Mixtures
Abstract
:1. The CSP Methodology
- its time scale, , which provides a measure of the time frame of its action
- its amplitude, , which provides a measure of its contribution to the evolution of the system
- the variables that pertain to this mode.
2. Autoignition of Ammonia
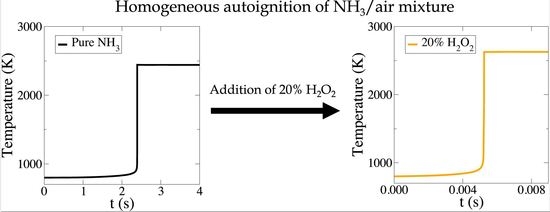
3. The Addition of HO
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CSP | Computational Singular Perturbation |
| IC | Internal Combustion |
| CI | Compression Ignition |
| SI | Spark Ignition |
| UHC | Unburnt Hydrocarbons |
| SIM | Slow Invariant Manifold |
| DME | Di-Methyl Ether |
| TPI | Timescale Participation Index |
| API | Amplitude Participation Index |
References
- Ryu, K.; Zacharakis-Jutz, G.E.; Kong, S.C. Effects of gaseous ammonia direct injection on performance characteristics of a spark-ignition engine. Appl. Energy 2014, 116, 206–215. [Google Scholar] [CrossRef]
- Zamfirescu, C.; Dincer, I. Ammonia as a green fuel and hydrogen source for vehicular applications. Fuel Process. Technol. 2009, 90, 729–737. [Google Scholar] [CrossRef]
- Frigo, S.; Gentili, R. Analysis of the behaviour of a 4-stroke SI engine fuelled with ammonia and hydrogen. Int. J. Hydrog. Energy 2013, 38, 1607–1615. [Google Scholar] [CrossRef]
- Reiter, A.J.; Kong, S.C. Demonstration of compression-ignition engine combustion using ammonia in reducing greenhouse gas emissions. Energy Fuels 2008, 22, 2963–2971. [Google Scholar] [CrossRef]
- Kroch, E. Ammonia, A Fuel for Motor Buses. J. Inst. Pet 1945, 31, 213–223. [Google Scholar]
- Duynslaegher, C.; Jeanmart, H.; Vandooren, J. Ammonia combustion at elevated pressure and temperature conditions. Fuel 2010, 89, 3540–3545. [Google Scholar] [CrossRef]
- Reiter, A.J.; Kong, S.C. Combustion and emissions characteristics of compression-ignition engine using dual ammonia-diesel fuel. Fuel 2011, 90, 87–97. [Google Scholar] [CrossRef]
- Gill, S.; Chatha, G.; Tsolakis, A.; Golunski, S.; York, A. Assessing the effects of partially decarbonising a diesel engine by co-fuelling with dissociated ammonia. Int. J. Hydrogen Energy 2012, 37, 6074–6083. [Google Scholar] [CrossRef]
- Saika, T.; Nakamura, M.; Nohara, T.; Ishimatsu, S. Study of hydrogen supply system with ammonia fuel. JSME Int. J. Ser. B Fluids Therm. Eng. 2006, 49, 78–83. [Google Scholar] [CrossRef]
- Li, J.; Huang, H.; Kobayashi, N.; He, Z.; Nagai, Y. Study on using hydrogen and ammonia as fuels: Combustion characteristics and NOx formation. Int. J. Energy Res. 2014, 38, 1214–1223. [Google Scholar] [CrossRef]
- Gross, C.W.; Kong, S.C. Performance characteristics of a compression-ignition engine using direct-injection ammonia–DME mixtures. Fuel 2013, 103, 1069–1079. [Google Scholar] [CrossRef]
- Li, J.; Huang, H.; Kobayashi, N.; Wang, C.; Yuan, H. Numerical study on laminar burning velocity and ignition delay time of ammonia flame with hydrogen addition. Energy 2017, 126, 796–809. [Google Scholar] [CrossRef]
- Kee, R.J.; Miller, J.A.; Jefferson, T.H. CHEMKIN: A General-Purpose, Problem-Independent, Transportable, FORTRAN Chemical Kinetics Code Package; Sandia Laboratories: Albuquerque, NM, USA, 1980. [Google Scholar]
- Li, J.; Huang, H.; Kobayashi, N.; He, Z.; Osaka, Y.; Zeng, T. Numerical study on effect of oxygen content in combustion air on ammonia combustion. Energy 2015, 93, 2053–2068. [Google Scholar] [CrossRef]
- He, X.; Shu, B.; Nascimento, D.; Moshammer, K.; Costa, M.; Fernandes, R. Auto-ignition kinetics of ammonia and ammonia/hydrogen mixtures at intermediate temperatures and high pressures. Combust. Flame 2019, 206, 189–200. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, C.W.; Somers, K.P.; Zhang, K.; Curran, H.J. The oxidation of 2-butene: A high pressure ignition delay, kinetic modeling study and reactivity comparison with isobutene and 1-butene. Proc. Combust. Inst. 2017, 36, 403–411. [Google Scholar] [CrossRef]
- Burke, U.; Metcalfe, W.K.; Burke, S.M.; Heufer, K.A.; Dagaut, P.; Curran, H.J. A detailed chemical kinetic modeling, ignition delay time and jet-stirred reactor study of methanol oxidation. Combust. Flame 2016, 165, 125–136. [Google Scholar] [CrossRef]
- Nakamura, H.; Hasegawa, S.; Tezuka, T. Kinetic modeling of ammonia/air weak flames in a micro flow reactor with a controlled temperature profile. Combust. Flame 2017, 185, 16–27. [Google Scholar] [CrossRef]
- Williams, F.A. Combustion Theory; The Benjamin/Cummings Publ. Co.: Menlo Park, CA, USA, 1985. [Google Scholar]
- Law, C.K. Combustion Physics; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Valorani, M.; Najm, H.N.; Goussis, D.A. CSP analysis of a transient flame-vortex interaction: Time scales and manifolds. Combust. Flame 2003, 134, 35–53. [Google Scholar] [CrossRef]
- Diamantis, D.J.; Mastorakos, E.; Goussis, D.A. H2/air Autoignition: The Nature and Interaction of the Developing Explosive Modes. Combust. Theor. Model. 2015, 19, 382–433. [Google Scholar] [CrossRef]
- Lam, S.H.; Goussis, D.A. Understanding complex chemical kinetics with Computational Singular Perturbation. Proc. Combust. Inst. 1989, 22, 931–941. [Google Scholar] [CrossRef]
- Lam, S.H.; Goussis, D.A. CSP method for simplifying kinetics. Int. J. Chem. Kinet. 1994, 26, 461–486. [Google Scholar] [CrossRef]
- Hadjinicolaou, M.; Goussis, D.A. Asymptotic solution of stiff PDEs with the CSP method: The reaction diffusion equation. SIAM J. Sci. Comput. 1998, 20, 781–810. [Google Scholar] [CrossRef]
- Goussis, D.A. The role of slow system dynamics in predicting the degeneracy of slow invariant manifolds: The case of vdP relaxation-oscillations. Physica D 2013, 248, 16–32. [Google Scholar] [CrossRef]
- Maris, D.T.; Goussis, D.A. The “hidden” dynamics of the Rössler attractor. Physica D 2015, 295–296, 66–90. [Google Scholar] [CrossRef]
- Najm, H.N.; Ponganis, D.; Prager, J. Analysis of NO structure in a methane-air edge flame. Proc. Combust. Inst. 2009, 32, 1117–1124. [Google Scholar] [CrossRef]
- Lu, T.; Yoo, C.; Chen, J.; Law, C.K. Three-dimensional direct numerical simulation of a turbulent lifted hydrogen jet flame in heated coflow: A chemical explosive mode analysis. J. Fluid Mech. 2010, 652, 45–64. [Google Scholar] [CrossRef]
- Goussis, D.A.; Valorani, M.; Creta, F.; Najm, H.N. Reactive and reactive-diffusive time scales in stiff reaction-diffusion systems. Prog. Comput. Fluid Dy. 2005, 5, 316–326. [Google Scholar] [CrossRef]
- Luo, Z.; Yoo, C.S.; Richardson, E.S.; Chen, J.H.; Law, C.K.; Lu, T. Chemical explosive mode analysis for a turbulent lifted ethylene jet flame in highly-heated coflow. Combust. Flame 2012, 159, 265–274. [Google Scholar] [CrossRef]
- Shan, R.; Yoo, C.S.; Chen, J.H.; Lu, T. Computational diagnostics for n-heptane flames with chemical explosive mode analysis. Combust. Flame 2012, 159, 3119–3127. [Google Scholar] [CrossRef]
- Kooshkbaghi, M.; Frouzakis, C.E.; Boulouchos, K.; Karlin, I.V. n-Heptane/air combustion in perfectly stirred reactors: Dynamics, bifurcations and dominant reactions at critical conditions. Combust. Flame 2015, 162, 3166–3179. [Google Scholar] [CrossRef]
- Tingas, E.A.; Kyritsis, D.C.; Goussis, D.A. Autoignition dynamics of DME/air and EtOH/air homogeneous mixtures. Combust. Flame 2015, 162, 3263–3276. [Google Scholar] [CrossRef]
- Goussis, D.A.; Najm, H.N. Model reduction and physical understanding of slowly oscillating processes: The circadian cycle. Multiscale Model. Simul. 2006, 5, 1297–1332. [Google Scholar] [CrossRef]
- Goussis, D.A.; Skevis, G. Nitrogen chemistry controlling steps in methane-air premixed flames. In Computational Fluid and Solid Mechanics; Bathe, K.J., Ed.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 650–653. [Google Scholar]
- Manias, D.M.; Diamantis, D.J.; Goussis, D.A. Algorithmic identification of the reactions related to the initial development of the time scale that characterizes CH 4/air autoignition. J. Energy Eng. 2014, 141, C4014015. [Google Scholar]
- Diamantis, D.; Kyritsis, D.; Goussis, D.A. Two stage ignition of n-heptane: Identifying the chemistry setting the explosive time scales. In Proceedings of the 2nd International Workshop on Model Reduction in Reacting Flows, Notre Dame, IN, USA, 30 March–1 April 2009; Univerity of Notre Dame: Notre Dame, IN, USA, 2009. [Google Scholar]
- Kourdis, P.D.; Palasantza, A.G.; Goussis, D.A. Algorithmic asymptotic analysis of the NF-kB signaling system. Comput. Math. Appl. 2013, 65, 1516–1534. [Google Scholar] [CrossRef]
- Shan, R.; Lu, T. A bifurcation analysis for limit flame phenomena of DME/air in perfectly stirred reactors. Combust. Flame 2014, 161, 1716–1723. [Google Scholar] [CrossRef]
- Diamantis, D.J.; Kyritsis, D.C.; Goussis, D.A. The reactions supporting or opposing the development of explosive modes: Auto-ignition of a homogeneous methane/air mixture. Proc. Combust. Inst. 2015, 35, 267–274. [Google Scholar] [CrossRef]
- Manias, D.M.; Tingas, E.A.; Frouzakis, C.E.; Boulouchos, K.; Goussis, D.A. The mechanism by which CH2O and H2O2 additives affect the autoignition of CH4/air mixtures. Combust. Flame 2016, 164, 111–125. [Google Scholar] [CrossRef]
- Tingas, E.A.; Kyritsis, D.C.; Goussis, D.A. Ignition delay control of DME/air and EtOH/air homogeneous autoignition with the use of various additives. Fuel 2016, 169, 15–24. [Google Scholar] [CrossRef]
- Tingas, E.A.; Kyritsis, D.C.; Goussis, D.A. Comparative investigation of homogeneous autoignition of DME/air and EtOH/air mixtures at low initial temperatures. Combust. Theory Model. 2017, 21, 93–119. [Google Scholar] [CrossRef]
- Tingas, E.A.; Kyritsis, D.C.; Goussis, D.A. Algorithmic determination of the mechanism through which H2O-dilution affects autoignition dynamics and NO formation in CH4/air mixtures. Fuel 2016, 183, 90–98. [Google Scholar] [CrossRef]
- Tingas, E.A.; Manias, D.M.; Sarathy, S.M.; Goussis, D.A. CH4/air homogeneous autoignition: A comparison of two chemical kinetics mechanisms. Fuel 2018, 223, 74–85. [Google Scholar] [CrossRef] [Green Version]
- Patsatzis, D.G.; Maris, D.T.; Goussis, D.A. Asymptotic analysis of a target-mediated drug disposition model: Algorithmic and traditional approaches. Bull. Math. Biol. 2016, 78, 1121–1161. [Google Scholar] [CrossRef] [PubMed]
- Goussis, D.A.; Lam, S.H. A study of homogeneous methanol oxidation kinetics using CSP. Proc. Combust. Inst. 1992, 24, 113–120. [Google Scholar] [CrossRef]
- Najm, H.N.; Valorani, M.; Goussis, D.A.; Prager, J. Analysis of methane-air edge flame structure. Combust. Theor. Model. 2010, 14, 257–294. [Google Scholar] [CrossRef]
- Prager, J.; Najm, H.N.; Valorani, M.; Goussis, D.A. Structure of n-heptane/air triple flames in partially-premixed mixing layers. Combust. Flame 2011, 158, 2128–2144. [Google Scholar] [CrossRef] [Green Version]
- Gupta, S.; Im, H.G.; Valorani, M. Classification of ignition regimes in HCCI combustion using computational singular perturbation. Proc. Combust. Inst. 2011, 33, 2991–2999. [Google Scholar] [CrossRef]
- Gupta, S.; Im, H.G.; Valorani, M. Analysis of n-heptane auto-ignition characteristics using computational singular perturbation. Proc. Combust. Inst. 2013, 34, 1125–1133. [Google Scholar] [CrossRef]
- Sarathy, S.M.; Tingas, E.A.; Nasir, E.F.; Detogni, A.; Wang, Z.; Farooq, A.; Im, H. Three-stage heat release in n-heptane auto-ignition. Proc. Combust. Inst. 2019, 37, 485–492. [Google Scholar] [CrossRef]
- Tingas, E.A.; Wang, Z.; Sarathy, S.M.; Im, H.G.; Goussis, D.A. Chemical kinetic insights into the ignition dynamics of n-hexane. Combust. Flame 2018, 188, 28–40. [Google Scholar] [CrossRef] [Green Version]
- Tingas, E.A.; Kyritsis, D.C.; Goussis, D.A. H2/Air Autoignition Dynamics around the Third Explosion Limit. J. Energ. Eng. 2018, 145, 04018074. [Google Scholar] [CrossRef]
- Manias, D.M.; Tingas, E.A.; Goussis, D.A. Algorithmic identification of the reactions that support or oppose the development of explosive modes in n-heptane/air autoignition. In Proceedings of the European Combustion Meeting, Budapest, Hungary, 30 March–2 April 2015. [Google Scholar]
- Tingas, E.A.; Im, H.G.; Kyritsis, D.C.; Goussis, D.A. The use of CO2 as an additive for ignition delay and pollutant control in CH4/air autoignition. Fuel 2018, 211, 898–905. [Google Scholar] [CrossRef]







| 3: | H + OH ↔ H + HO | 70b: | NH + HO ← NH + HO | |
| 5f: | O + H → O + OH | 71f: | NH + HO → HNO + OH | |
| 18f: | HO (+M) → OH + OH (+M) | 110f: | NH + NH → NH + H | |
| 31f: | H + O (+M) → HO (+M) | 146b: | NH (+M) ← NH + NH (+M) | |
| 63f: | NH + NO → NNH + OH | 156b: | NH + OH ← NH + HNO | |
| 64f: | NH + NO → N + HO | 208f: | HNO + NH → HNO + NH |
| P | P | P | P | P |
|---|---|---|---|---|
| t = 0.222 s | t = 1.263 s | t = 2.3763 s | t = 2.39505 s | t = 2.39507 s |
| = 1.23(1) | = 9.50(-1) | = 5.89(1) | = 4.30(4) | = 6.32(5) |
| TPI | ||||
| 18f: +0.20 | 156b: +0.14 | 18f: +0.15 | 5f: +0.15 | 5f: +0.24 |
| 110f: +0.08 | 18f: +0.13 | 208f: −0.10 | 63f: +0.05 | 3f: +0.08 |
| 64f: −0.08 | 208f: −0.11 | 156b: +0.10 | 64f: −0.05 | 31f: −0.06 |
| 71f: +0.08 | 70b: −0.07 | 146b: +0.09 | 3f: +0.05 | 3b: −0.06 |
| 156b: +0.06 | 146b: +0.06 | 64f: −0.08 | ||
| 63f: +0.06 | 63f: +0.07 | |||
| 64f: −0.06 | ||||
| API | ||||
| 18f: +0.16 | 156b: +0.15 | 18f: +0.14 | 5f: +0.10 | 5f: +0.22 |
| 110f: +0.14 | 18f: +0.12 | 156b: +0.11 | 64f: −0.05 | 31f: −0.10 |
| 71f: +0.09 | 208f: −0.11 | 208f: −0.10 | 63f: +0.05 | 3f: +0.06 |
| 156b: +0.06 | 70b: −0.08 | 146b: +0.09 | ||
| 146b: +0.07 | 64f: −0.08 | |||
| 63f: +0.07 | ||||
| Po | ||||
| HO: +0.74 | T: +0.90 | T: +0.89 | T: +1.14 | T: +1.39 |
| HNO: +0.10 | HO: +0.08 | HO: +0.09 | NH: −0.09 | O: −0.18 |
| HO: −0.08 | HO: −0.14 | |||
| O: −0.08 | NH: −0.12 | |||
| H: +0.06 | H: −0.11 | |||
| OH: +0.08 | ||||
| Case | (s) | Reduced | % Change | (K) | Increased | % Change |
|---|---|---|---|---|---|---|
| Pure NH | 2.395 | - | - | 2442.41 | - | - |
| 2% HO | 8.38(−2) | 28.6 | −96.50% | 2456.48 | 1.01 | 0.58% |
| 10% HO | 9.66(−3) | 247.9 | −99.60% | 2523.72 | 1.03 | 3.33% |
| 20% HO | 5.24(−3) | 456.9 | −99.78% | 2627.36 | 1.08 | 7.57% |
| 30% HO | 3.83(−3) | 625.7 | −99.84% | 2760.47 | 1.13 | 13.02% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalil, A.T.; Manias, D.M.; Tingas, E.-A.; Kyritsis, D.C.; Goussis, D.A. Algorithmic Analysis of Chemical Dynamics of the Autoignition of NH3–H2O2/Air Mixtures. Energies 2019, 12, 4422. https://doi.org/10.3390/en12234422
Khalil AT, Manias DM, Tingas E-A, Kyritsis DC, Goussis DA. Algorithmic Analysis of Chemical Dynamics of the Autoignition of NH3–H2O2/Air Mixtures. Energies. 2019; 12(23):4422. https://doi.org/10.3390/en12234422
Chicago/Turabian StyleKhalil, Ahmed T., Dimitris M. Manias, Efstathios-Al. Tingas, Dimitrios C. Kyritsis, and Dimitris A. Goussis. 2019. "Algorithmic Analysis of Chemical Dynamics of the Autoignition of NH3–H2O2/Air Mixtures" Energies 12, no. 23: 4422. https://doi.org/10.3390/en12234422
APA StyleKhalil, A. T., Manias, D. M., Tingas, E. -A., Kyritsis, D. C., & Goussis, D. A. (2019). Algorithmic Analysis of Chemical Dynamics of the Autoignition of NH3–H2O2/Air Mixtures. Energies, 12(23), 4422. https://doi.org/10.3390/en12234422