Economic Dispatch of BESS and Renewable Generators in DC Microgrids Using Voltage-Dependent Load Models

Abstract

This paper addresses the optimal dispatch problem for battery energy storage systems (BESSs) in direct current (DC) mode for an operational period of 24 h. The problem is represented by a nonlinear programming (NLP) model that was formulated using an exponential voltage-dependent load model, which is the main contribution of this paper. An artificial neural network was employed for the short-term prediction of available renewable energy from wind and photovoltaic sources. The NLP model was solved by using the general algebraic modeling system (GAMS) to implement a 30-node test feeder composed of four renewable generators and three batteries. Simulation results demonstrate that the cost reduction for a daily operation is drastically affected by the operating conditions of the BESS, as well as the type of load model used.

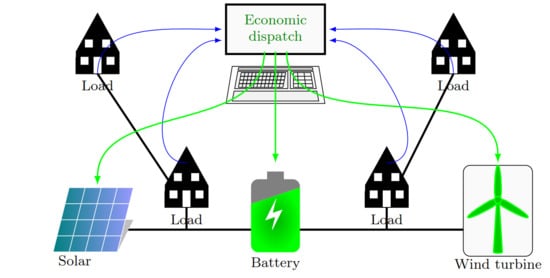
1. Introduction

The integration of multiple renewable energy resources in electrical networks has mostly been driven by global concerns about the effects of global warming. Renewable energy integration is regarded as a solution that can mitigate this problem by minimizing greenhouse gas emissions, which are primarily produced by transport and energy systems [1,2]. These generation technologies are intended to replace the fossil fuels used for electricity generation gradually. The most studied renewable power generation systems are photovoltaic solar and wind generation technologies, which produce sustainable energy and reduce greenhouse gas emissions [3] by extracting energy from solar radiation and wind speed for conversion to electrical energy. Nevertheless, because of its inherently stochastic nature and dependence on weather conditions, this type of generation is associated with many uncertainties, which must be taken into account during electrical planning processes and even short-term grid operation (typically, as economic dispatch problems) [4].

A viable solution that tackles the characteristic variability of renewable energy sources is their conversion into constant and reliable energy sources through the optimal integration of batteries (such as lithium-ion, lead–acid, and nickel–cadmium batteries). These batteries can store energy during periods of high generation and low demand and inject power during periods of low generation and high consumption. For this purpose, efficient dispatch strategies must be established to ensure the adequate operation of the whole grid. The inclusion of battery energy storage systems (BESSs) in electrical networks is independent of the operational characteristic of the network; that is, the electrical grid can be operated in alternating current (AC) [5] or direct current (DC) mode [3]. The possibility of integrating BESSs lies in the incorporation of AC or DC devices that use power electronic converters to manage the power interchange between them and the grid [1,2].

DC microgrids are more attractive than AC microgrids because they have several advantages that their AC counterparts lack. For example, DC microgrids have lower losses, greater reliability, higher efficiency, and a simpler connection, and they do not require synchronization. Additionally, DC microgrids do not need frequency and reactive power control [6]. DC microgrids are composed of renewable energy, energy storage devices, and electronic loads, which are interconnected by means of DC/DC power converters. Their efficiency is improved by the simplicity of their control states and the reduction in energy conversion stages [7].

In this study, we focus on DC microgrids with a high penetration of renewable generation from photovoltaic and wind technologies. We evaluate an economic dispatch problem for these grids by short forecasting using artificial neural networks, as reported in [3]. In addition, our approach includes a sensitivity analysis based on different load models using an exponential load representation to determine the impact on the profits predicted by the daily economic dispatch model.

The specialized literature includes a variety of works that have studied this topic. In [3], a convex optimization model was proposed for analyzing the day-ahead economic dispatch problem in DC microgrids with BESSs and renewable generation. However, the study included only a static load model, so the impact of constant current and constant impedance loads during daily operations could not be determined. In [8], an efficient operation scheme was proposed for BESS systems in AC distribution networks with a constant power load model, but the model did not consider the stochastic variation in photovoltaic and wind generation. The authors of [9,10] proposed dynamic stochastic models for operating BESS systems with short forecasting predictions in microgrid applications by using artificial neural networks and a model predictive approach. Nevertheless, these approaches focused on AC grids with constant power loads. Multiple authors have previously proposed the integration and operation of a BESS system in electrical networks with optimization methods such as convex relaxation with multi-stage stochastic planning [11,12,13], multi-agent models based on market decisions [14], heuristic cost–benefit analysis [15], multi-objective genetic algorithms [16], multi-objective particle swarm optimization [17,18], and bee colony optimization [19]. A complete description of BESS allocation methods can be found in [20].

It is important to highlight that the above-mentioned BESS allocation methods are for AC grids with long planning periods. In contrast, our aim is to propose a day-ahead operation method for BESS systems in DC microgrids with a high penetration of renewable generation. Since this concept has only been addressed in [3,21], there is ample opportunity to expand current knowledge on this topic. For this purpose, we performed a sensitivity analysis based on an exponential voltage-dependent load model by using a short forecasting load method based on artificial neuronal networks (ANNs). The exponential voltage-dependent load model is implemented because it represents a suitable formulation for power flow problems since with a single exponent the linear combination of ZIP loads can be obtained in a simplified way, while the ZIP model requires three exponents. In addition, this representation permits making voltage analysis stability by keeping a relationship directly between the voltages of loads and sources. To solve the proposed nonlinear non-convex model, which represents the optimal day-ahead operation of BESSs in DC microgrids with a high penetration of renewable generation, we employed the general algebraic modeling system (GAMS) and its nonlinear optimization packages, as recommended in [3,8,22,23].

The remainder of this paper is organized as follows. Section 2 presents the mathematical model that represents the day-ahead operation of BESS systems in DC microgrids with renewable generation for power cost minimization. Section 3 describes the short-forecasting approach based on ANNs for predicting the power output of photovoltaic and wind generation from solar radiation, temperature, pressure, humidity, and time inputs. Section 4 provides the GAMS code for a small six-node DC test feeder that can be used by graduate and undergraduate students to identify potential applications of this software in power system optimization scenarios. Section 5 presents the numerical validation of the proposed approach in a DC microgrid composed of 21 nodes with a radial structure, two renewable generators, and three BESSs for typical Colombian demand and generation scenarios. Concluding remarks are reported in Section 6.

2. Mathematical Model

The economic dispatch problem in DC microgrids for a daily operation with renewable generation and energy storage technologies is a nonlinear non-convex optimization problem whose economic objective function is related to energy production (buying) costs, as well as nonlinear constraints related to the technical aspects associated with power grid operation.

Objective function

$$minz=\sum _{t\in \mathcal{T}}\sum _{i\in \mathcal{N}}Co{E}_{i,t}{p}_{i,t}\mathsf{\Delta }t$$

(1)

where z represents the objective function value, $Co{E}_{i,t}$ is the cost of buying energy at node i in period t, $p_{i,t}$ is the power bought at node i during period t, and $\mathsf{\Delta }t$ is the length of the time period under analysis (e.g., 1 h or 15 min). $\mathcal{T}$ and $\mathcal{N}$ are the sets that contain all periods of time considered and the total number of nodes in the DC microgrid, respectively.

Set of constraints

$$p_{i,t}+p_{i,t}^{dg}+p_{i,t}^b-p_{i,t}^d=v_{i,t}\sum _{j\in \mathcal{N}}{G}_{ij}{v}_{j,t},\{\forall i\in \mathcal{N}\&\forall t\in \mathcal{T}\}$$

(2)

$$So{C}_{i,t}^b=So{C}_{i,t-1}^b-{\phi }_i^b{p}_{i,t}^b\mathsf{\Delta }t,\{\forall i\in \mathcal{N}\&\forall t\in \mathcal{T}\}$$

(3)

$$So{C}_{i,t_0}^b=So{C}_i^{b,ini},\{\forall i\in \mathcal{N}\}$$

(4)

$$So{C}_{i,t_f}^b=So{C}_i^{b,fin},\{\forall i\in \mathcal{N}\}$$

(5)

$$p_{i,t}^{min}\le p_{i,t}\le p_{i,t}^{max},\{\forall i\in \mathcal{N}\&\forall t\in \mathcal{T}\}$$

(6)

$$p_{i,t}^{dg,min}\le p_{i,t}^{dg}\le p_{i,t}^{dg,max},\{\forall i\in \mathcal{N}\&\forall t\in \mathcal{T}\}$$

(7)

$$p_i^{b,min}\le p_{i,t}^b\le p_i^{b,max},\{\forall i\in \mathcal{N}\&\forall t\in \mathcal{T}\}$$

(8)

$$v_i^{min}\le v_{i,t}\le v_i^{max},\{\forall i\in \mathcal{N}\&\forall t\in \mathcal{T}\}$$

(9)

$$So{C}_i^{b,min}\le So{C}_{i,t}^b\le So{C}_i^{b,max},\{\forall i\in \mathcal{N}\&\forall t\in \mathcal{T}\}$$

(10)

where $p_{i,t}^{dg}$, $p_{i,t}^b$, and $p_{i,t}^d$ are the power generation by renewable energy resources (i.e., distributed generation), the power delivered/absorbed by the batteries, and the power demand at node i during the time period t, respectively. $So{C}_{i,t}^b$ represents the state of charge of the battery in the ith node at the tth time period. $v_{i,t}$ represents the voltage profile at node i during period t, and $G_{ij}$ corresponds to the ${ij}^t$ component of the conductance matrix associated with the physical connection of the nodes through DC branches. $So{C}_i^{b,ini}$ and $So{C}_i^{b,fin}$ are the initial and final desired states of charge of the batteries, while $So{C}_i^{b,min}$ and $So{C}_i^{b,max}$ are the maximum and upper state-of-charge bounds. $p_{i,t}^{min}$, $p_{i,t}^{max}$, $p_{i,t}^{dg,min}$, and $p_{i,t}^{dg,max}$ are the minimum and maximum bounds of admissible generation for conventional and renewable generators located in the ith node in time period t, while $p_i^{b,min}$ and $p_i^{b,max}$ represent the minimum and maximum charge/discharge capabilities of a battery connected at node i. $v_i^{min}$ and $v_i^{max}$ are the voltage regulation bounds of the DC microgrid. Finally, ${\phi }_i^b$ represents the coefficient of charge of a battery connected at node i.

Remark 1.

The economic dispatch model for operating BESSs in DC microgrids on a DC power grid defined in Equations (1)–(10) was previously proposed in [3]. The main difference in this work is the inclusion of voltage-dependent load modeling, which has not yet been reported in the specialized literature.

The specialized literature includes two widely used models for modeling voltage-dependent load behaviors. The first model corresponds to an exponential representation of the voltage dependence, and the second model is a polynomial model known as the ZIP model [24]; the two models are equivalent [25]. We selected the exponential model to represent the voltage dependence on the demand nodes. This exponential representation is

$$\begin{array}{c}\hfill p_{i,t}^d=p_{i,t}^{d0}{\left(\frac{v_{i,t}}{v_{nom}}\right)}^{{\alpha }_i},\{\forall i\in \mathcal{N}\&\forall t\in \mathcal{T}\}\end{array}$$

(11)

where $p_{i,t}^{d0}$ corresponds to the base constant power consumption under nominal voltage operating conditions at node i during time period t, and ${\alpha }_i$ is the exponential coefficient of the load connected at node i.

Remark 2.

If the parameter ${\alpha }_i$ in the exponential load model connected at node i is assigned the value of 2, then the load is modeled as constant resistive consumption. If this parameter takes the value of 1, then the load is modeled as constant current. If ${\alpha }_i$ takes the value of 0, then the load model corresponds to the classical constant power representation.

The proposed optimization model for solving economic dispatch problems in DC microgrids is nonlinear non-convex because Equation (2) contains products between the voltage variables $v_{i,t}$ and $v_{j,t}$. This turns the right-hand side of Equation (2) into a quadratic set of non-affine constraints that, in conjunction with the exponential load model, permit multiple solutions.

To demonstrate that the ZIP and exponential load models are equivalent in certain operating conditions, namely, constant power, constant impedance, and constant current scenarios, we define the polynomial model as follows:

$$\begin{array}{c}\hfill p_{i,t}^d=p_{i,t}^{d0}\left(a_i+b_i\left(\frac{v_{i,t}}{v_{nom}}\right)+c_i{\left(\frac{v_{i,t}}{v_{nom}}\right)}^2\right),\{\forall i\in \mathcal{N}\&\forall t\in \mathcal{T}\}\end{array}$$

(12)

where $a_i\ge 0$, $b_i\ge 0$, and $c_i\ge 0$ represent the coefficients of the constant power, constant current, and constant impedance components, respectively. In addition, $a_i+b_i+c_i=1$ must hold since each factor represents the percentage of the type of load present in node i. With these factors, we can select three special cases in which the ZIP and exponential models represent the same load.

• If $a_i=1$, then $b_i=0$ and $c_i=0$, implying that the ZIP model takes only the component associated with the power, i.e., the constant power representation, which is completely equivalent to ${\alpha }_i=0$ in the exponential model.
• If $b_i=1$, then $a_i=0$ and $c_i=0$, implying that the ZIP model takes only the component associated with the current, i.e., the constant current representation, which is completely equivalent to ${\alpha }_i=1$ in the exponential model.
• If $c_i=1$, then $a_i=0$ and $b_i=0$, implying that the ZIP model takes only the component associated with the impedance, i.e., the constant impedance representation, which is completely equivalent to ${\alpha }_i=2$ in the exponential model.

In addition, any possible combination of the coefficients $a_i$, $b_i$, and $c_{i}0$ can be represented by a real number associated with the exponential load model. This exponent (${\alpha }_i$) can be obtained by applying a Taylor’s series expansion over Equation (11) and comparing it with Equation (12).

3. Short-Term Forecasting for Renewable Generation

The high variability of distributed generation using renewable resources means that the power outputs from these sources in the operation of an electrical distribution network are difficult to predict. The day-ahead economic dispatch requires the determination of the short-term forecast for power generation in photovoltaic systems and wind turbines. Multiple approaches have been proposed for this purpose, including the similar-day approach [26,27], fuzzy logic [28,29], stochastic optimization, and artificial neural networks [29,30]. Based on the conventional and frequently used approaches, for this investigation, we selected the artificial neural network (ANN) that was recently reported in [3] to predict the power outputs of wind turbines (WTs) and photovoltaic (PV) plants. The inputs are humidity, pressure, temperature, time, wind speed, and solar radiation.

Remark 3.

Short-term forecasting of renewable generation is a key component of an electric distribution operation for utilities since, normally, companies entrusted with a national grid operation define their operation for 24 h using a day-ahead economic dispatch. Thus, utilities need to take short-term forecasting into account for the accurate and real operation of their networks [31].

The main characteristics and structure of ANNs are introduced in the next section.

3.1. An Artificial Neural Network

An ANN is a computational model that represents and exploits the main learning characteristics of the human brain; they work with interconnected layers of nodes that emulate neuronal connections. An ANN can be used for pattern recognition, the forecasting of future events, or data classification based on an initial training dataset. Figure 1 presents the conventional structure of an ANN implemented in MATLAB for solar prediction using two inputs [3].

A neural network can be decomposed into layers of abstraction. It can be trained with multiple types of input information to recognize different behaviors according to a particular set of inputs or measures. For example, it can be used to control the position of a pendulum by reading its state variables (inverse design) [32] or predict renewable generation outputs according to current weather conditions [3]. The behavior of an ANN is defined by the manner in which its individual elements are connected and by the strength or weights of those connections (see the w and b parameters in Figure 1). These weights are automatically adjusted during training according to a specified learning rule until the neural network performs the desired task correctly [33]. In the next section, we briefly explain the ANN used for predicting the available solar and wind power to predict the day-ahead economic dispatch.

3.2. The Nonlinear Autoregressive Exogenous Neural Network

A nonlinear autoregressive exogenous (NARX) neural network is a dynamic recurrent ANN with feedback connections enclosing several layers that help to predict stochastic variables by using historical information [3]. This information is used to train the ANN by using the following rule

$$\begin{array}{c}\hfill y\left(t\right)=f\left(y(t-1),...,y(t-n_y),x(t-1),...,x(t-n_x)\right)\end{array}$$

(13)

where x corresponds to the set of exogenous inputs, while y is the desired output, which depends on the last $n_y$ values of the variable being predicted, and t represents the current time to which the prediction applies.

Table 1. Input parameters and desired outputs for wind and solar generation forecasting.

Photovoltaic		Wind
Inputs	Output	Inputs	Output
Temperature	Solar Radiation	Temperature	Wind speed
		Humidity
Time		Pressure
		Time

presents the set of inputs for predicting solar radiation and wind speed for photovoltaic and wind generation applications.

The process of training the NARX network for predicting solar radiation and wind speed was implemented in MATLAB software via ntstool using 2 inputs, 6 delays, and 18 hidden neurons for the photovoltaic case and 4 inputs, 4 delays, and 12 neurons for the wind generation case, as recommended in [3]. We used 70% of the data for training and 15% for adjusting and validating the ANN in this study. Finally, Figure 2 shows the solar and wind power information that

4. Proposed Solution Method

The solution of the proposed nonlinear convex optimization model for the optimal operation of BESSs in DC microgrids was produced in this study by using the general algebraic modeling system, widely known as GAMS. This is a nonlinear large-scale optimization software program applied for general simulation purposes. The main characteristics of GAMS software are listed below.

✓

It is possible to use a compact formulation by implementing a set representation.

✓

Its mathematical structure preserves the same nature of the symbolic model, which facilitates numerical implementation.

✓

It can solve a range of problems, from linear programming optimization problems to nonlinear mixed-integer programming problems (non-convex formulations).

✓

It has a free version for demonstration, so it is useful for introducing engineering students to mathematical optimization.

✓

The implementation of any mathematical model in GAMS only requires basic programming skills. In addition, it uses a unique plain interface with reserve words that facilitate their mathematical implementations.

Basic Elements for GAMS Implementation

Any mathematical optimization formulation in GAMS [34] can be implemented by following the structure presented in Algorithm 1.

Algorithm 1: The main steps of implementing an optimization model in GAMS.

Data: Selection of the test system.  Sets Definition of sets, scalar, parameters (constant vectors), and tables (constant matrices).;  Variables: Determine the nature of variables, e.g., binary, integer, or continuous.;  Equations: Write the set of equations that represent the optimization problem, i.e., (1)–(10).;  Solution: Solve the mathematical model using an NLP solver for minimization.;  Visualization: Print the variables of interest, i.e., states of charge in batteries or voltages.;  Result: Optimal scheme for scheduling BESS in DC microgrids.

More details on using reserved words and more commands to implement mathematical models in GAMS are found in [35,36]. Appendix A shows an example of the implementation of the proposed mathematical model given in Equations (1)–(10).

5. Test System and Simulation Scenarios

This section presents the main characteristics of the test system, as well as the simulation scenarios.

5.1. The 30-Node Test System

The 30-node test feeder is a DC distribution grid operated with 13.8 kV and a total load of 5.85 MW (these values correspond to a classical AC distribution test feeder for Colombian utilities [8]). The grid configuration of this test feeder is depicted in Figure 3, and the conductor parameters of this test system are summarized in

Table 2. Information about the conductors of the test system.

Type	Caliber AWG/kcmil	Resistance [$\mathsf{\Omega }/$km]	Max. Current [A]
1	4	1.360	138
2	2	0.854	185
3	266.8	0.213	443

, in which the caliber and resistance per kilometer are reported (these values are taken from CENTELSA company for cables ACC [37]).

Table 3. Information about branches and consumption of the 30-node test feeder.

Node i	Node j	Type of Conductor	Length [km]	${\mathit{p}}_{\mathit{j}}^{\mathit{d}0}$ [kW]
1	2	1	1.75	100
1	3	3	1.25	0
3	4	1	0.75	500
4	5	1	0.25	350
5	6	1	0.40	150
3	7	1	0.50	0
7	8	1	0.45	400
7	9	1	0.80	300
3	10	3	1.85	0
10	11	1	0.75	400
11	12	1	1.00	175
12	13	1	0.40	225
10	14	3	0.85	0
14	15	3	1.70	0
15	16	1	0.52	0
16	17	1	0.15	200
16	18	1	0.42	150
14	19	2	0.28	0
19	20	2	0.35	250
19	21	2	0.45	150
21	22	2	0.75	0
22	23	2	0.26	600
22	24	2	0.34	500
22	25	2	0.17	300
18	26	2	0.85	450
26	27	1	0.42	200
15	28	1	1.40	100
28	29	1	0.75	150
23	30	1	0.82	200

reports the length of each branch, the type of conductor, and the peak load at the receiving node.

For this test feeder, we considered four renewable generators, which have an aggregated maximum power capability of 4 MW and are distributed as follows: two PV generators are located at nodes 9 and 18 with installed capacities of 850 and 1150 kW, respectively, and two wind generators are located at nodes 12 and 21 with maximum power capabilities of 600 and 1400 kW, respectively. In addition, we considered the inclusion of three large-scale energy storage systems with the capabilities reported in

Table 4. Energy storage capabilities and locations.

Location	Energy [kWh]	Time of Charge/Discharge [h]
3	1500	3
15	2000	5
22	1200	4

.

It is important to mention that the lifespan, energy density, and power output capabilities depend on the battery technology and can thus change drastically [38]. In this study, we considered lithium-ion batteries, which have between 3 and 15 years of continuous operation as a function of the dispatch methodology employed for their operation [38]. In addition, the costs of acquisition can oscillate between 600 and 3800 US$/kWh. The data reported in Table 4 show that the energy storage capabilities of the batteries in this study are 1200, 1500, and 2000 kWh. Given the required times for charge/discharge, their power capabilities are 400 and 500 kW, respectively.

For additional information about operational and installation costs, as well as the recommended maximum and minimum states of charge, consult References [38,39].

Figure 4 presents the real and predicted power outputs of the renewable generators, the percentage load variation, and the cost of power generation at the slack node during the day. All of this information is included in the Appendix to provide an opportunity to validate this approach.

The real curves shown in Figure 4 were obtained using online data for solar radiation, wind speed, temperature, pressure, and humidity for time periods of 1.5 h. This information, which can be found in [40], was used to obtain the PV and WT power outputs presented in Figure 2. To determine the estimated (predicted) curves of generation for photovoltaic systems and wind turbines, we used 70% of the data to train the proposed ANN, and the remaining 30% of the dataset was employed in the validation scenario. In this regard, in our numerical results, we selected an arbitrary day from the validation set and designated it as the real curve. In addition, we used the ANN for the predictions. Figure 4 reports the real and estimated power outputs, which clearly demonstrate that ANNs are an excellent tool for the short-term forecasting of renewables.

5.2. Simulation Scenarios

To validate the proposed mathematical model, we considered the following three simulation scenarios:

• Scenario 1 (${\mathbf{S}}_1$): Optimal dispatch with the BESS starting and finishing the daily operation in the totally discharged state.
• Scenario 2 (${\mathbf{S}}_2$): Optimal dispatch with the BESS starting and finishing the daily operation with a 50% charge, with the possibility that the states of charge vary from 0% to 100% during the day.
• Scenario 3 (${\mathbf{S}}_3$): Optimal dispatch with the BESS starting and finishing the daily operation with a 50% charge, with the possibility that the states of charge vary from 50% to 100% during the day.

For all simulation scenarios, we varied the exponential load coefficient from 0 to 2 in steps of 0.5 in order to identify the effect of the load model on the daily economic dispatch of the network. In addition, for all simulations, we contrasted the predicted generation given by the artificial neural network with the real output of the power generation to determine the efficiency and robustness of the proposed economic dispatch model. For all simulations, we assumed that the system operates with a resolution of 0.5 h. Furthermore, for the peak of the electricity, we applied the information reported by the utility CODENSA for Colombia in May 2019, which is COP$/kWh 479.3389.

6. Numerical Results

All simulations were carried out on a desktop computer running on INTEL(R) Core(TM) i7-7700, 3.60 GHz, 8 GB RAM with 64-bit Windows 10 Pro using GAMS 25.1.3 with the nonlinear large-scale solver CONOPT4 (Supplementary Materials).

6.1. Comparison between Real and Projected Cases

Table 5. Operating costs during a daily operation for the different operating scenarios (values in MCOP$, i.e., millions of Colombian pesos).

Case	$\mathit{\alpha }=0.0$	$\mathit{\alpha }=0.5$	$\mathit{\alpha }=1.0$	$\mathit{\alpha }=1.5$	$\mathit{\alpha }=2.0$
Scenario 1
Real	18.4526	18.2860	18.1239	17.9661	17.8121
Expected	18.2310	18.0668	17.9069	17.7513	17.5994
Scenario 2
Real	18.4336	18.2631	18.0973	17.9358	17.7784
Expected	18.2122	18.0441	17.8805	17.7212	17.5659
Scenario 3
Real	18.6883	18.5133	18.3432	18.1776	18.0164
Expected	18.4665	18.2939	18.1260	17.9627	17.8036

reports the numerical performance of the proposed economic dispatch model for operating renewable generators and batteries with different operating conditions. First, it is important to mention that the effect of the exponential coefficient of the load directly affects the final operating cost in both cases (real and expected generation). For example, in ${\mathbf{S}}_1$, we observe that, when $\alpha =0$ (constant power load), the total operating cost per day is 18.4526 MCOP$ (millions of Colombian pesos); for $\alpha =2$ (constant resistive load), the cost is 17.8121 MCOP$, which is a difference of about 0.6405 MCOP$ and confirms that the load model can significantly affect the expected operating cost of the utility. These variations are considered to be uncertainties in the planning process. Figure 5 presents the differences between the real and expected operating costs when the exponential load coefficient is located at the extremes. From this picture, it is clear that the differences between load models remain quasi-constant for real and expected generation cases. In addition, the operating conditions (scenarios) do not significantly affect the final costs, which implies that they are not strongly correlated under different load models.

Next, Figure 6 shows the estimation error for the final operational costs when ANNs are used to predict the generation for the next day compared with the final result when using the real curve. This picture shows that, for practical purposes, in the proposed test system, the average expected estimation error of the ANN is about 1.20% for all the simulation scenarios, and it has a decreasing tendency when the load model changes from a constant power load to a constant resistive load.

It is important to mention that each simulation condition (a combination of the battery parameters and the exponential coefficient) was solved in less than 700 ms. Thus, GAMS proves to be an excellent tool for solving economic dispatch problems since it can evaluate multiple scenarios before the real validation.

6.2. Additional Results

To verify that all the batteries are within their operating bounds, we selected the second scenario with constant power loads for the expected case. Figure 7a reports the state of charge of each battery during the daily operation. It is possible to observe that all the batteries effectively begin and finish the day with a 50% load, while, during the day, the state of charge varies from 0% to 100%, as defined in ${\mathbf{S}}_2$. From the results obtained for the batteries, we can conclude the following (all comments below are related to the plots presented in Figure 4):

• During the first eight periods (4 h), all batteries achieve 100% load. This behavior can be attributed to the possibility of buying energy at low prices during this period, which also coincides with low power consumption.
• Between Periods 18 and 24, the batteries experience continuous discharges. This behavior coincides with high increases in load consumption, while photovoltaic generation is simultaneously increasing from zero to its maximum; this implies that not all the capability of renewable generation is available to supply all the demand. For this reason, the batteries help to supply it.
• Between Periods 24 and 32, the batteries begin to charge until they reach maximum values, taking advantage of the renewable generation peaks.
• When the load reaches the maximum value and photovoltaic power generation starts to decrease, all the batteries discharge their available power to reduce the cost. This occurs from Period 32 to 40.
• Finally, from Period 43 (and Period 44), all the batteries start to increase their states of charge from 0% until the end of the daily operation, at which time they are at 50%. These changes in the states of charge of all the batteries occur after Period 43 since the cost of power generation is lower at this time, which also coincides with low power consumption.

For the voltage performance, Figure 7b demonstrates that all the nodes for all the time periods remain between 0.975 and 1.005 pu. Therefore, the worst voltage regulation is 2.5%, which is very small compared with the conventional bounds ($\pm 10\%$) for medium-voltage grids in Colombia [8].

7. Conclusions and Future Works

In this paper, we propose a nonlinear programming model that represents the problem of economic dispatch of DC microgrids with a high penetration of renewable generators and energy storage systems. The renewable energy generation was predicted with recursive artificial neural networks considering different inputs, such as temperature, pressure, humidity, and time. Different operating scenarios were tested to observe the effect of several operating conditions that can be implemented by utilities. The main contribution of this research is the exponential load model for the economic dispatch, which demonstrates the effect of the expected operating costs as a function of the load model. Additionally, the exponential voltage-dependent load model allowed having a representation of ZIP loads with single exponent, which is a suitable formulation for power flow problems. The results of the models reveal that a constant power load is the most expensive scenario, and a constant resistive load is the least expensive. All simulation scenarios were developed using the GAMS package as an optimizer, which has a user-friendly interface that permits the development of a consistent mathematical model that is not found with the solution technique. Further, solutions with the model were found with faster convergence times (less than 1 s in all simulation scenarios).

The artificial neural network used to predict the potential generation for dispatching all the batteries shows that the estimation error of the final costs is lower than 1.21%, which confirms that it is a powerful tool for modeling the operation of electrical networks that require accurate predictions in short periods of time.

Future work may include the development of an optimization strategy for reallocating available batteries in order to minimize the operational cost of the grid by reducing the active power loss during the charging/discharging processes. Additional work may also entail the proposal of a metaheuristic algorithm to locate renewable generators and batteries in DC microgrids in a master-slave approach for minimizing power losses and operational costs, especially in rural or non-interconnected grids.