Neural Network Based Model Comparison for Intraday Electricity Price Forecasting

Abstract

The intraday electricity markets are continuous trade platforms for each hour of the day and have specific characteristics. These markets have shown an increasing number of transactions due to the requirement of close to delivery electricity trade. Recently, intraday electricity price market research has seen a rapid increase in a number of works for price prediction. However, most of these works focus on the features and descriptive statistics of the intraday electricity markets and overlook the comparison of different available models. In this paper, we compare a variety of methods including neural networks to predict intraday electricity market prices in Turkish intraday market. The recurrent neural networks methods outperform the classical methods. Furthermore, gated recurrent unit network architecture achieves the best results with a mean absolute error of 0.978 and a root mean square error of 1.302. Moreover, our results indicate that day-ahead market price of the corresponding hour is a key feature for intraday price forecasting and estimating spread values with day-ahead prices proves to be a more efficient method for prediction.

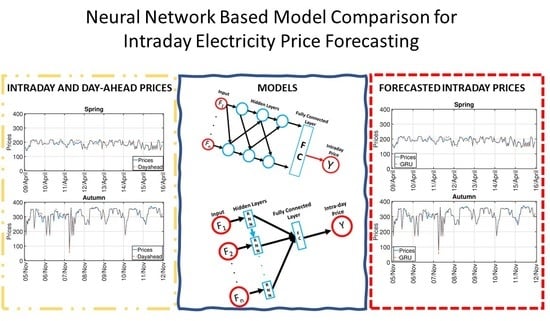
1. Introduction

Electricity price forecasting literature has improved significantly since the beginning of the 2000s [1,2,3,4,5]. Although there are many articles about electricity price forecasting, which have been discussed in the reviews [6,7,8], most of the research is in the spot markets, which are called day-ahead markets widely. Generally in these markets electricity prices are forecasted and submitted to the system until noon for each hour of the next day. Then, the market-maker sets the clearing price of each hour according to the intersection of the supply and demand curves in this auction-based market [9,10,11]. Aggarwal et al. [6] mention the superiority of different models in different markets and conclude the article with the hope of the new computational tools’ success in the electricity price forecasting in the future. Today, in addition to the ensemble prediction [12], Lasso regression [13,14], and hybrid methods [15,16,17,18,19], deep learning models [20,21,22,23] are the most successful ones in the electricity price forecasting accuracy.

1.1. Intraday Electricity Market

One of the most important features of the electricity is the requirement of the constant balance between supply and demand. Unfortunately, day-ahead markets are not sufficient to balance the requirements of the electricity consumers. On the other hand, electricity suppliers also need a platform to sell the excess electricity after the settlement of the electricity prices and the quantities in the day-ahead markets. Due to the requirement of close to delivery electricity trade, balancing and/or intraday markets are constituted in most countries. The balancing/intraday markets are continuous trade platforms for each hour of the day. After the prices are settled at about 14:00 in the day-ahead markets, balancing/intraday markets start to trade at about 18:00 for each hour of the next day. Trade in the balancing/intraday market can be done until a few hours before the delivery. For instance, in the developed German EPEX intraday market, trade continues until just 15 min before the delivery [24,25,26]. In the Turkish intraday market, electricity is tradeable from 18:00 of the previous day until one hour before the delivery.

Due to the importance of the intraday markets, especially for the balancing purposes, trade of electricity in the regulated markets moves from the day-ahead markets to the balancing/intraday markets quite swiftly. The number of trades and the quantities show an increasing trend in the intraday markets. In this sense, starting from the 2010s, intraday electricity market research is also in a developing trend. However, pioneer articles in the field are generally about the features and descriptives of the intraday electricity markets [24,27,28,29]. A number of articles investigate the effect of the renewables on the intraday electricity prices [30,31,32,33]. The effect of balancing forecast errors of the renewables on the intraday electricity prices are discussed in [34] and the realized volatility of the German-Austrian intraday market is modeled and forecasted by GARCH models in [35]. The article of Kath and Ziel [36] is particularly important to show the economic value of the intraday electricity price forecasting success. A very recent review [37] about the intraday electricity markets discusses the literature in detail considering different types of research in the area.

1.2. Intraday Electricity Price Forecasting

To the best of our knowledge, articles about intraday electricity price forecasting are limited. Two relatively early papers [38,39] forecast the electricity prices in the Iberian electricity market. In [38] the authors apply a single-layer artificial neural network (ANN) technique on the six intraday sessions of the market. They include chronological, price, demand, weather, and power generation variables step-wise to have different forecasting models. In five of the six sessions, only the hourly prices of the day-ahead market and the hourly prices of the previous intraday sessions, which are named chronological variables, decrease the mean absolute percentage error (MAPE). In the intraday session 6, the best model utilizes the hourly prices of the previous sessions, in addition to the chronological variables. Although forecasting for a year had become the rule of thumb in the electricity price forecasting literature to have robust results, in this paper, out of sample period is only the chosen weeks of a year and the paper focuses on the variable selection in the intraday market. Andrade et al. [39] perform probabilistic price forecasting, which is an improving research area [8] in the Iberian day-ahead and intraday markets. By using the combination of linear quantile regression and gradient boosting trees, they investigate the effect of the renewables variables. Additionally, they also adjust the forecasts by using the daily average spot price.

Another variable selection and forecasting paper [13] includes many variables and applies Lasso technique to select from them. According to the results, most important variables are the most recent intraday prices and the day-ahead prices of the corresponding hour. In contrast to the day-ahead market, the previous day’s intraday price for the same hour is not effective. Another interesting finding is that the intraday price for hour 24 and the nearby evening hours have an important effect. A very recent paper [40] forecasts the price spread of the day-ahead and intraday markets and evaluates the economic benefit [36] of having accurate electricity price forecasts. ARX and Probit methods are applied in the German and Polish markets to forecast the price spread. Especially using the forecast of the wind generation, in addition to the endogenous variables, can predict the sign of the price spread successfully. As it is in line with the literature [41,42], they conclude that correct sign classifications do not necessarily correspond to the financial effect. In a related paper [43] Narajewski and Ziel forecast the ID3 Price in the German Intraday market. ID3 Price is the quantity-weighted average of all trades until 3 h before delivery for the predicted hour. They forecast by using different Lasso and elastic net models, then compare the results with the naive methods. Although results of different methods are very close to each other, the best method is the naive method, which takes the most recent price of the corresponding hourly product. As in [13], this paper also checks the statistical significance of the forecasts’ outperformance by Diebold-Mariano test [44]. Their main finding is very similar with the main finding of [13], which is that most of the explanatory information of the intraday prices are on the most recent intraday trade for hourly products. However, it must be taken into account that the German intraday market is the most mature and liquid market of Europe, which might cause this result.

1.3. Contributions

The motivation of our research is the lack of intraday electricity price forecasting methods’ comparison in the literature. Moreover, recurrent neural networks (RNN) such as long-short term memory (LSTM) and gated recurrent units (GRU) are not investigated in the intraday markets. Furthermore, neural networks, which have one layer, are only applied in one paper [38]. In this research, we will compare the utility of neural networks for intraday price forecasting. Additionally, effect of the endogenous and exogenous variables will also be discussed. Another point of contribution is the expansion of the intraday electricity market research to the Turkish market. To the best of our knowledge, the only examined markets were the German, Polish, and Iberian intraday markets. Most importantly, statistical methods such as linear regression, Lasso, and the machine learning methods such as ANN, LSTM, and GRU are compared in a comprehensive way in this intraday electricity price forecasting research.

The remainder of the paper is structured as follows. Section 2 discusses the data with its specific features. In Section 3, we explain the methods that will be used to forecast the electricity prices, in addition to the forecast performance measures. In Section 4, results are given from various perspectives. Consequently, Section 5 wraps up the results and concludes with further research ideas.

2. Data

Hourly intraday electricity prices of the Turkish Intraday Market are obtained from 1 January 2017 to 28 February 2019 [45]. Estimation (Training) period is taken as 14 months, from 1 January 2017 to 28 February 2018. Test period is the remaining time frame of the data, which is from 1 March 2018 to 28 February 2019. In this paper, we work with the quantity-weighted averages of the electricity prices for each hour. Moreover, exogenous variables, day-ahead prices, balancing market prices, renewables/total generation, forecast demand/supply, and trade values in the day-ahead market are taken from the same platform [45].

The dependent variable, intraday price, is the quantity weighted average of all the trades of the contract. Day-ahead price (F1) is the correspondent day-ahead price, which is set in the day-ahead market at 14:00 of the previous day for each contract of the intraday market. Balancing market is an intermediary market between day-ahead and intraday markets, prices of which (F2) we use in the forecast of intraday prices. Forecast renewables, including hydro, supply over total generation (F3) is taken as another variable to represent the effect of the renewables on the intraday prices. Forecast demand/supply (reserve margin) (F4) is an extensively used variable in the day-ahead electricity price forecasting. We will check its effect in the intraday market. As the last independent variable, trade value in the day-ahead market (F5) for the contract is used to examine the effect of quantity.

Table 1. Utilized features for electricity price estimation.

Symbol	Feature	Availability
F1	Day-ahead price	from 14:00 previous day
F2	Balancing market price	3 hours in advance
F3	Forecast Renewables/Total generation	from 18:00 previous day
F4	Forecast demand/supply	from 18:00 previous day
F5	Trade Value (day-ahead market)	from 14:00 previous day

summarizes the features we will use in this paper with corresponding codes and their availability period. The availability period [46] and the forecasted dependent variable [43] differ from market to market. As our dependent variable is the quantity-weighted average price and our models are already trained in the estimation (training) period, the forecasting availability is directly related to the availability of the exogenous variables (Table 1).

Electricity prices have a high level of seasonality in various frequencies. Therefore, the prices differ considerably in the day-time as well as in the seasons of the year. The seasonality throughout the days of the week and the seasons of the year can be seen in Figure 1. Moreover, intraday seasonality can be followed from

Table 2. Statistics of the intraday electricity prices (Turkish Lira/MWh) according to the hours of the day.

Hours	Mean	Standard Deviation	Upper Bound	Lower Bound	Median
0	235.07	71.33	357.80	4.56	212.91
1	234.26	65.75	355.49	4.77	212.25
2	209.52	67.80	353.28	4.55	197.15
3	194.49	69.96	350.68	2.31	185.39
4	183.64	74.21	352.22	2.26	178.62
5	199.76	72.32	359.08	2.31	188.32
6	200.59	66.17	355.73	4.28	189.16
7	217.80	70.22	356.21	2.53	202.65
8	246.42	77.17	360.19	5.33	231.12
9	255.72	76.72	366.31	1.98	271.16
10	255.63	74.02	368.89	6.40	270.64
11	262.78	71.43	378.24	7.45	285.49
12	238.53	72.44	373.48	6.52	228.45
13	246.58	74.72	380.13	6.60	240.49
14	257.72	69.81	383.39	6.79	252.14
15	255.95	73.34	382.91	8.34	253.54
16	262.11	70.48	384.86	6.86	271.63
17	266.48	69.77	381.15	6.43	289.57
18	265.48	69.61	377.28	8.99	294.91
19	265.71	64.32	371.88	125.06	286.45
20	266.99	61.23	371.34	148.6	281.09
21	264.68	60.37	371.31	131.14	273.23
22	245.97	62.62	365.46	65.41	256.59
23	227.45	66.03	358.42	34.72	218.72

.

Figure 1 illustrates intraday and day-ahead prices from the sample weeks of each season between March 2018 and February 2019. The sample weeks are chosen randomly. Firstly, it is important to mention that day-ahead and intraday prices are very close to each other in all seasons. Secondly, prices are very volatile in the winter week, which is due to the requirement of heating in the winter season. Spring prices are the least volatile ones due to the high level of renewables share in the generation. Regarding the temperature differences in the autumn months, autumn prices are also volatile like winter prices but in a less smooth way. Lastly, day-ahead and intraday prices differ especially at the more volatile periods, like the winter week. On the other hand, prices are almost equal throughout the spring week.

Table 2 represents the high prices from 08:00 to 22:00. In the early morning hours 02:00 to 06:00, when the energy demand is the lowest, electricity prices are at the lowest levels. Moreover, standard deviation is at the top levels in the morning hours, especially at about 08:00 and 09:00. For most of the hours, the lower bound of the prices throughout the year is just above 0 Lira and the upper bound is just below 400 Liras. When we check the difference between mean and median, we can observe the skewness in both directions varying according to the hours of the day.

In

Table 3. Statistics of the spread (difference of the intraday electricity prices with the day-ahead electricity prices (Turkish Lira/MWh)) according to the hours of the day.

Hours	Mean	Standard Deviation	Upper Bound	Lower Bound	Median
0	−2.30	6.31	59.78	−24.63	−1.86
1	−2.55	6.35	30.94	−38.02	−1.51
2	−1.56	6.93	42.64	−32.21	−0.82
3	−1.25	6.36	32.30	−36.23	−1.25
4	−0.30	8.01	59.57	−54.84	−0.46
5	−1.45	6.97	33.97	−39.12	−1.07
6	−1.34	8.25	70.96	−36.11	−1.07
7	−1.94	7.42	56.12	−45.31	−1.38
8	−2.57	7.37	18.41	−77.55	−1.38
9	−2.60	7.27	12.73	−70.71	−1.24
10	−1.64	5.63	17.09	−31.06	−1.07
11	−0.69	7.30	87.14	−38.19	−0.31
12	0.03	6.41	29.79	−24.78	0.00
13	−0.19	6.73	25.70	−29.07	−0.05
14	−1.00	6.77	17.24	−34.99	−0.43
15	−0.56	6.80	21.43	−39.27	0.05
16	−1.00	7.28	20.34	−41.79	−0.34
17	−1.10	7.56	46.52	−30.75	−0.08
18	−1.34	7.77	25.52	−30.49	0.09
19	−1.37	7.64	17.85	−40.94	−0.31
20	−1.77	7.96	52.70	−37.57	−0.52
21	−1.83	7.13	15.74	−36.02	−0.77
22	−0.90	7.66	78.52	−27.20	−0.44
23	−0.27	8.56	98.01	−32.95	−0.11

, we have the spread of the intraday and day-ahead electricity prices in the Turkish electricity market. Day-ahead price is the day-ahead electricity price for the same hour, which is set in the day-ahead market on the previous day. The difference between the intraday market price and the day-ahead market price for the same hour gives us the spread. Firstly, all hours except 12:00 have a positive mean, which means that intraday prices are lower than the day-ahead prices. Secondly, mean prices are distributed around zero. However, standard deviations are quite high compared to the corresponding mean prices. We can see this effect in the upper and lower bounds as well. The range is over 50 Turkish Liras/MWh for all hours except 10:00. Lastly, regarding median, there is a positive skewness in the data, which means the median of the intraday and day-ahead price difference is lower than the mean of the price difference. Thus, we can say that the large differences in the upper tail of the distribution affect the means greatly.

3. Methods

Our fundamental idea in this paper is to compare a variety of techniques for intraday price forecasting. In this section, we will detail all methodologies that are utilized for intraday price forecasting, ranging from statistical models to neural network based methods. First of all, naive method, which is used as benchmark in this paper is given in Section 3.1. In Section 3.2, we give the regression equation, which shows the dependent and independent variables. In Section 3.3 we give a brief definition of Lasso model. In Section 3.4, fundamentals of neural network are introduced and details of the utilized ANN architecture are provided. In Section 3.5, the general concept of RNNs is introduced. In Section 3.6 and Section 3.7, specific RNN architectures, LSTMs, and GRU are defined respectively. We mention the implementation details and parameter setup in Section 3.8. Finally, we give the evaluation metrics in Section 3.9.

3.1. Naive Method

In this paper, day-ahead price is taken as the benchmark to compare with the various methods’ forecasts. Thus, our benchmark, which is called naive method in this paper is the corresponding hour’s day-ahead price as seen in Equation (1)

$$Y_t=F{1}_t,$$

(1)

where $Y_t$ is the intraday price to be predicted and $F{1}_t$ is day-ahead price, which is determined 24 h in advance. Generally it is very difficult to outperform the naive method due to the high correlation between intraday and day-ahead electricity prices.

3.2. Multivariate Linear Regression

In our linear regression model, the dependent variable is the intraday electricity price and independent variables are the features F1–F5, which were added step-wise to the regression. This regression model is applied to observe the difference between the naive baseline day-ahead method and the regressions. The regression Equation (2) is below,

$$Y_t=w_0+w_{1}F{1}_t+w_{2}F{2}_t+w_{3}F{3}_t+w_{4}F{4}_t+w_{5}F{5}_t+{ϵ}_t,$$

(2)

where $Y_t$ is the intraday price to be predicted, ws are non-random unknown parameters, $F{1}_t–F{5}_t$ are non-random and observable values, and ${ϵ}_t$ is independently and identically distributed (i.i.d).

3.3. Lasso Regression

The least absolute shrinkage and selection operator (LASSO) [47] method is used widely in the electricity price forecasting [13,14,48] literature due to its capability of reducing the number of features, on which the given solution is dependent. Equation (3) shows the loss function over parameters w, which minimizes the sum of residual sum of squares and the $L_1$ penalty for ensuring sparse solutions.

$$\underset{w}{\min }\frac{1}{\left(2n_{\mathrm{samples}}\right)}\ast \left|\right|Y-F{w}_2^2\left|\right|+{\lambda \ast \left|\right|w\left|\right|}_1,$$

(3)

where $n_{\mathrm{samples}}$ is the total number of samples to train from, Y is the intraday electricity price, F is the available input features, and $\lambda$ ≥ 0 is the regularization parameter. If $\lambda$ = 0, then it is a regular least squares estimator. Selecting a good value for $\lambda$ is critical. In this paper, we used a grid search to optimize the parameter and used $\lambda =1$ in our experiments.

3.4. Artificial Neural Networks

ANNs have become the state-of-the-art algorithm in machine learning. Generally speaking they are based on densely connected neurons [49], where weight and bias terms are learnt at every neuron. For the task of intraday electricity price estimation we used various combinations of features defined in Table 1 and a 3-layer neural network. Each hidden layer consists of 10 neurons and there is a final layer to predict the price value as visualized in Figure 2.

3.5. Recurrent Neural Networks

RNNs have sequential input by definition and the neurons of the network store the current state in order to inform the next time step. In particular, RNN achieves this by recurrent connections between the nodes. The guiding equation for hidden state $h_t$, for a sequence of inputs $x=(x_1,x_2,\dots ,x_T)$ is:

$$h_t=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}(t=0)\hfill \\ \varphi (h_{t-1},x_t),\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(4)

where $\varphi$ should be a non-linear function. The update of the recurrent hidden state is defined by:

$$h_t=g(W{x}_t+U{h}_{t-1})$$

(5)

where g is a hyperbolic tangent function.

One common issue for this guiding equation is the vanishing gradients. To overcome this issue, two RNN architectures are proposed, namely LSTM and GRU, which we utilize for our experiments in this work as visualized in Figure 3. In our implementation of RNNs, we give the features as an input and 50 blocks are used for training that are connected to a fully connected layer with 1 node for prediction of the electricity price.

3.6. Long Short Term Memory

An LSTM is designed with three specific gates: an input gate, a forget gate, and an output gate [50]. Typically, a sigmoid function is applied to the inputs and the previous hidden state $h_{t-1}$. The fundamental aim of the LSTM is to generate the current hidden state at time t. LSTM takes in old cell state and outputs its new cell state, which enables LSTM to maintain information in memory for long periods of time. This property is particularly helpful for LSTMs to address the vanishing gradient problem.

3.7. Gated Recurrent Units

The original architecture of GRU is designed with two gates: an update gate and a reset gate [51]. The update gate aims to define which proportion of the previous memory should be kept and the reset gate decides on the combination of the new input with the previously accumulated memory. A common property of LSTM is to control which state is being exposed thanks to a three gate structure. GRUs that do not have that property can receive information from whole hidden content. There is no particular control of GRU on this phenomena, which makes them less complicated and easier to train.

3.8. Implementation Details

In our implementations of neural networks, we utilize the Keras deep learning framework with Tensorflow library. As optimizer we use Adam optimized with a learning rate of $1\times {10}^{-4}$ and a momentum of 0.9. We initialize the training of the neurons from a zero-mean Gaussian distribution. A batch size of 100 h is used for training. The training is stopped when a certain number of epochs is reached (5000) or if there is no substantial improvement to the training loss after 20 epochs (%1). For the linear regression, the weights have been determined as: $w_1=0.86299718$, $w_2=0.0482890693$, $w_3=-2.30291939$, $w_4=10.7312573$, and $w_5=0.00000267$.

3.9. Evaluation Metrics

To evaluate each method we use mean absolute error (MAE) and root mean square error (RMSE) metrics. Equation (6) shows the MAE formula and Equation (7) shows RMSE between the predicted price ${\widehat{P}}_i$ and the actual prices $P_i$ for the hour i in total number of T hours.

$$\mathrm{MAE}=\frac{1}{T}\sum _{i=1}^T\left|P_i-{\widehat{P}}_i\right|$$

(6)

$$\mathrm{RMSE}=\sqrt{\frac{1}{T}\sum _{i=1}^T{\left(P_i-{\widehat{P}}_i\right)}^2}$$

(7)

4. Results

This section presents quantitative and qualitative evaluation of the experimental results. Our quantitative analysis consists of comparing a variety of methods with evaluation metrics and statistical significance tests. The qualitative results illustrate the weekly performance in sample weeks from each season. We report the results on actual price value inputs in Section 4.1 and the results on spread value inputs in Section 4.2. Finally, we show the statistical significance of the reported results in Section 4.4.

4.1. Price Prediction on Actual Values

We use the actual price values for training and testing in our experimental setup. We use all features including day-ahead prices on all algorithms and show the results in

Table 4. Mean absolute error (MAE) results for training on actual values for predictive models.

Features	Naive	Regression	Lasso	ANN	LSTM	GRU
F1	4.736	4.908	5.472	5.153	5.153	4.719
F1-2	4.736	4.505	4.802	4.692	4.726	4.490
F1-3	4.736	4.616	4.802	4.906	4.694	4.496
F1-4	4.736	6.118	4.802	4.796	4.487	4.407
F1-5	4.736	5.763	4.961	4.708	4.479	4.393

and

Table 5. Root mean square error (RMSE) results for training on actual values for predictive models.

Features	Naive	Regression	Lasso	ANN	LSTM	GRU
F1	7.374	7.283	7.696	7.911	7.911	7.202
F1-2	7.374	6.884	7.047	7.379	7.416	6.912
F1-3	7.374	6.933	7.047	7.590	7.348	7.073
F1-4	7.374	8.200	7.047	7.514	7.142	6.919
F1-5	7.374	7.952	7.214	7.033	6.895	6.857

. Linear regression works best, when only day-ahead is used as a feature, which is expected due to the close values between the intraday and day-ahaead values as illustrated in Figure 1. In general ANN outperforms Lasso and Regression but shows worse performance compared to LSTM and GRU. The introduction of additional input features increases the performance of neural network based methods. GRU outperforms all the methods when all features are given as input.

4.2. Price Prediction on Spread Values

By using the results from Section 4.1, we decided on continuing with the most successful results in the spread prediction. Therefore, we used F1-5 and F2-5 in our spread predictions. The reason for applying F2-5 is having results without day-ahead prices (F1). Regarding the spread already covering the day-ahead price, we checked the effect of using day-ahead price as an independent variable. However, we find that using day-ahead price to estimate the spread has a positive effect on the accuracy of our forecast.

In

Table 6. MAE results for spread training of predictive models.

Features	Naive	Regression	Lasso	ANN	LSTM	GRU
F2-5	4.736	4.828	4.722	1.715	1.634	1.181
F1-5	4.736	5.763	4.926	1.668	1.325	0.978

and

Table 7. RMSE results for spread training of predictive models.

Features	Naive	Regression	Lasso	ANN	LSTM	GRU
F2-5	7.374	7.231	7.190	2.170	2.382	1.719
F1-5	7.374	7.952	7.182	2.323	1.785	1.302

, we give MAE and RMSE results of the spread prediction according to various methods, respectively. Spread forecasts are transformed back to the actual electricity prices before the calculation of the MAE and RMSE values in Table 6 and Table 7. Results show us that the errors decrease substantially by using spreads. For instance, MAE value is less than 1 Turkish Liras/MWh for F1-5 GRU method.

4.3. Seasonal Prediction Results

We show the prediction results of our best performing method (GRU) for the weeks defined in Section 2. Figure 4 shows the performance of GRU (the best performing model) using all five features on actual prices. In winter and autumn, GRU shows a good match to the actual price. However, the fluctuations in summer and spring challenge the forecasting, and errors are visible for these two weeks.

Figure 5 shows the performance of GRU on spread prices. The method is able to show a great alignment with the intraday prices in all seasons. In particular, the spikes are captured with great accuracy. The week from 7 to 12 January shows great volatility, which challenged the estimation with actual prices as illustrated in Figure 4. The introduction of spread helps the GRU method to come up with accurate predictions for the challenging winter week. The same performance increase can be observed in the calmer week in spring, when using the spread values.

4.4. Diebold-Mariano Tests

To test statistical significance of the results in Table 4 and Table 6, we use Diebold-Mariano tests [44], which is the state-of-the-art method to evaluate significance. In Figure 6a, we illustrate the p-values for the Diebold-Mariano tests for the actual price prediction of the performance. Figure 6b focuses on the results presented in Table 6 for spread prediction.

The experiment illustrated in Figure 6 is a color map representation of the p-values achieved as a result of comparing two methods at a time. If the I-values are low (represented in green), the method in the horizontal axis is superior to the method in the vertical axis in a statistically significant manner. The F1-5 GRU model outperforms all the other models in a statistically significant manner in both comparisons. The results demonstrate the successful performance of the neural network models compared to the classical methods. In particular, superior results are achieved using RNNs, namely GRU and LSTM, which is evident with the low p-values.

5. Discussion

We have presented a comprehensive analysis on different forecasting models for predicting intraday electricity prices. In particular, we have illustrated that neural network based methods are capable of estimating prices more accurately compared to Lasso and linear regression models. Recurrent neural network architectures have outperformed the ANN in a statistically significant manner according to Diebold-Mariano tests. This finding is in line with the previous studies [20,21] for time series type problems. Time-dependent tasks can be addressed with algorithms that have the ability to remember previous time-points. RNNs are capable of remembering previous time points thanks to their memory component. GRU has shown better performance compared to LSTM as illustrated in actual price prediction and spread prediction results in Table 4 and Table 6. Our extensive experimental results underlined the successful performance of neural network based methods and they should be considered in future studies in intraday price prediction.

Another key observation of our paper is the better performance of prediction on spread between day-ahead and intraday prices compared to prediction on actual prices. This improvement is evident in particular for neural network methods, when the results in Table 4 and Table 6 are compared. The same observation holds for RMSE results in Table 5 and Table 7. This can be explained with the descriptive statistics of spread and actual prices introduced in Section 2. The spread has a smaller solution space due to the fact that intraday and day-ahead prices are close. Therefore, spread is a better way to train the forecasting models and evaluate them.

In this paper, we forecast the weighted intraday prices which are very close to the day-ahead prices, as seen in Figure 1. Therefore, the intraday price forecasting problem is very similar to the day-ahead one. The methods which are used in the intraday electricity price forecasting so far, such as ARX [40,43], probit [40], Lasso [13,43], neural networks [38], and probabilistic methods [39], are also very similar to the models in the day-ahead electricity price forecasting. In the meantime, it also explains the importance of the day-ahead price as an independent variable in the intraday electricity price forecasting models. Uniejewski et al. [13] conclude that day-ahead price of the corresponding hour is one of the most important variables in intraday price forecasting.

In addition to the corresponding hour’s day-ahead price, we used four more variables (Table 1) in this paper, which increased the accuracy of our forecasts. F2 is the balancing market price which is a specific market to the country. We used these prices as information for the intraday market. F3 is the forecast renewables/total generation, which is announced by [45] the day before the trade. This information is not available by the due time of the day-ahead market bidding. Therefore, it is important to understand the difference between the day-ahead and intraday prices. The effect of renewables on the intraday electricity prices is also proven to be prominent [30,33]. Forecast demand/supply (F4), or reserve margin in other words, has an important effect on day-ahead price forecasting. We investigated its effect in the intraday price forecasting. Along with the trade value of the day-ahead market (F5), which represents the volume traded, they both (F4 and F5) have a marginal effect on the intraday electricity prices.

As a relatively new research area, future research of intraday electricity price forecasting can go in many different directions. The positive economic effect of using spreads is discussed in [40]. The financial effect of these forecasts can be further discussed. Due to the model comparison focus of this paper, the feature selection was not the priority. According to [13,43] most recent intraday price is a very important variable. This variable may be added as a feature in the future work. The generalizability of the electricity price forecasting research to the other countries is a questionable topic due to the different features and settings of the markets. Therefore, the most important future research that our paper will trigger is the application of neural networks, especially recurrent neural networks, in various intraday markets. Last but not least, the amount of available trade data in the intraday markets will make the neural network based methods a natural choice for the intraday price forecasting applications in the future.