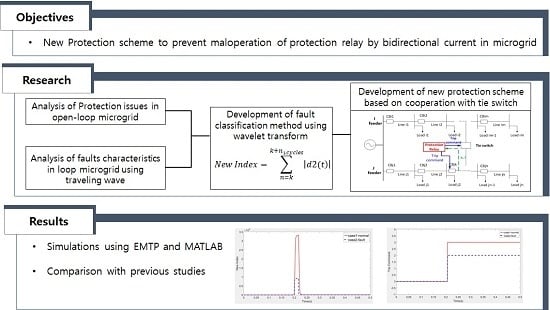
New Protection Scheme Based on Coordination with Tie Switch in an Open-Loop Microgrid

Abstract

Owing to the increase in renewable energy, microgrids (MGs) are increasing. A MG has a small loop-type grid configuration. In the loop MG, challenges in protection such as maloperation of protection relay may occur owing to bidirectional current flow. Herein, we propose a new protection scheme in the loop MG. Considerations for protection in loop MG and fault characteristics are analyzed. Based on these, a new index to solve the considerations for MG protection are proposed using a wavelet transform. Furthermore, the new protection scheme based on the coordination with tie switch using the proposed new index is proposed. To verify the proposed scheme, the MG and the proposed scheme are modeled using the electromagnetic transients program and MATLAB. Various simulations according to the fault location and the success/failure of fault section separation are performed. Simulation results indicate that the power supply on the original feeder can be maintained by proposed method.

1. Introduction

Currently, the reliability requirements for electric power supplies are increasing as a result of the increase in sensitive loads and power demands. In addition, the connections of distributed generation and energy storage system are increasing as well. Hence, the distribution system is changing from a radial distribution system to a loop distribution system, including microgrids (MGs) [1]. A MG can be defined as a small loop-type distribution system. In the loop power distribution system, challenges in protection may occur owing to bidirectional current flow. The protection issues in the MG can be raised by the same reason. Therefore, we examine the previous works on protection issues in the loop distribution system.

The loop distribution system can be divided into an open-loop/closed-loop distribution system according to the normal open/close of the tie switch. In the open-loop distribution system, the maloperation of a protection relay may occur owing to the tie switch operation. Meanwhile, in the closed-loop distribution system, the maloperation of the protection relay may occur owing to directional problems caused by bidirectional current flow [1]. Various studies have been conducted on the protection issues of the loop distribution system. The fault characteristics of the loop distribution system have been studied. In [2], the fault current in a weakly meshed power distribution system was analyzed. In [3], the fault characteristics in the distribution system connected with a photovoltaic system were analyzed. In [4], the fault characteristics in a closed-loop power distribution system with cables were analyzed. In [5], the location and capacity of the fault current limiter for fault current reduction in the loop distribution system was studied. In [6], fault location using wavelet transform and support vector machine technology in the loop distribution system was studied. Some studies have focused on the protection scheme and fault detection. In [1], a countermeasure against the tie switch operation in an open-loop system was proposed. However, this method is disadvantageous because the circuit breaker of the original distribution line is opened in spite of the fault at the other distribution line, and the blackout can be enlarged. In [7], a pilot protection relay scheme was proposed for a closed-loop power distribution system with a cable. In [8], a high-resistance fault detection method was proposed in a mesh distribution system. In [9], the performance of directional protection relays in the medium voltage loop network has been compared. In [10], an adaptive fault detection method using a probabilistic neural network was proposed in a loop power distribution system. In [11,12], the protection schemes for a microgrid were studied. Some studies have addressed the protection coordination in a loop distribution system. In [13], an optimal protection coordination method for the overcurrent relay in a loop power distribution system was proposed using the nature-inspired root tree algorithm. In [14], an optimization method for the time-dial setting of the directional overcurrent relay in the closed-loop power distribution system was proposed. In [15], it was proposed coordination of protection, which is adaptive and optimal using firefly algorithm and artificial neural network to obtain optimal coordination. This study was tested on a modified Institute of Electrical and Electronic Engineers (IEEE) 9 bus loop system with the addition of distributed generation (DG). In [16], a protection coordination method was proposed using a distributed dual power supply using a dual simplex algorithm.

Herein, we address the protection issue considering the operation of the tie switch in the open-loop system. In [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16], protection issues in a closed-loop system were addressed; however, the operation of the tie switch was not considered except in [1]. To solve the problem in [1], we propose a new protection scheme based on the coordination with a tie switch.

Wavelet transforms (WTs) have been used in power system protection because they can be used in a wide range of frequency bands. In [17,18], WT was applied to develop the reclosing algorithm in a distribution system. In [19,20], WT was applied to fault detection and classification. In [21], WT was applied to microgrid protection. In [22], WT was applied to directional protection. In [23], WT was applied to the fault detection in a low voltage direct current (DC) distribution system. Therefore, WT can be applied to protection issues. In this study, we use WT to develop the fault classification method for a new protection scheme.

Compared with the previous works mentioned above, the new contributions of our paper are as follows:

(1)

Considerations for the protection in the loop MG are analyzed.

(2)

The fault characteristics according to the tie switch operation in the loop MG are analyzed using traveling wave.

(3)

This paper proposes a new index that can distinguish the fault at another feeder, the normal load current supply to another feeder, and the fault at the original feeder using WT.

(4)

We propose a new protection scheme based on the coordination with a tie switch using a new index.

(5)

We model the MG using the electromagnetic transients program (EMTP) and implement the proposed protection method using MATLAB. From the simulation results, we prove the superiority of the proposed scheme by comparing it with previous studies.

This paper is organized as follows: Section 2 investigates the considerations for protection in the loop MG. Section 3 analyzes the fault characteristics of the loop MG using the traveling wave according to the operating conditions of a tie switch. In Section 4, we propose a new index that can determine the fault at others feeder, the normal load current supply to another feeder, and the fault at the original feeder. In Section 5, we propose a new protection scheme based on the coordination with a tie switch using the new index discussed in Section 4. Section 6 discusses the simulation results to verify the proposed method using the MG model. By comparing the results with those of the previous studies, we prove the superiority of the proposed method. Finally, the conclusions derived from the study are presented in Section 7.

2. Considerations on Protection Issues in an Open-Loop MG

Figure 1 shows the loop MG model, where the tie switch is typically open. The tie switch is typically open at normal states; therefore, it is a separate radial system in which the I and J feeders are separated. However, when a fault occurs, problems not considered in a radial system must be addressed.

The first consideration pertains to the normal load current being supplied from the J feeder to the I feeder. If a fault occurs at fault 1, circuit breaker i1 (CB i1) is opened, and CBi2 is also opened to isolate the fault Section. Subsequently, the tie switch is closed, and the normal load current is supplied from the J feeder to the I feeder. If the load capacities of the remaining Section in the I feeder are large, the overcurrent relay (OCR) connected to the CBjk near the tie switch in the J feeder detects the overcurrent, and a trip command can be issued to open the CBjk despite the normal load current. That is, the protection relay may exhibit a maloperation. In this case, the best solution is to block the trip command of the OCR because it is a normal load current supply.

The second consideration pertains to the failed isolation of the fault Section because of a failed CBi2 operation. However, the tie switch can be closed without recognizing the failure of the fault Section separation. Therefore, the fault current can be injected from the J feeder. Subsequently, the CBjk in the J feeder will be opened by a trip command of the OCR. If this occurs, the CBjk will open even though the J feeder is not faulty, and the remaining J feeder will experience an outage. The best solution for this case is to ensure that the protection relays in the J feeder operates CBi2. However, long-distance communication facilitating between the protection relay and CBi2 must be connected. Another solution is to reopen the tie switch. In this method, the tie switch can be controlled simultaneously by the protection relay connected to CBjk, such that a relatively long communication facility is not required. Herein, we propose a new protection method by adopting the second method, which is the opening of the tie switch.

The third consideration pertains to a fault occurring at fault 2 that is located at the latter part of the tie switch in the J feeder. In this case, the tie switch is open and the OCR connected to the CBjk can issue a trip command for an instantaneous or time-inverse trip. In other words, the OCR should operate normally.

In summary, the following issues should be considered in the new protection method.

(1)

If the fault Section is typically disconnected, the protective relay should not operate because the normal load current is supplied from the J feeder to the I feeder.

(2)

If the separation of the fault Section fails and the tie switch is closed, the fault current can be injected from the J feeder. In this case, the tie switch must be opened again.

(3)

If the fault occurs in the latter part of the tie switch in the J feeder, the protection relay should operate normally.

3. Characteristics of Faults in the Loop MG

This Section analyzes the characteristics of faults to develop new protection methods in open-loop MGs based on the analysis in Section 2. In Figure 1, if the fault occurs in the I feeder, it can be divided into the success and failure of fault Section separation. In both cases, the tie switch is closed and a traveling wave is generated. If a fault occurs at the J feeder, a transient traveling wave may also occur. Therefore, characteristics of the traveling wave must be examined.

3.1. Case of Success of Fault Section Separation (Normal Load Current Supply from J feeder)

First, we examine the case of a successful fault Section separation, that is, a normal load current supply. After the tie switch is closed, a traveling wave is generated. The traveling wave travels along the I feeder. When the traveling wave meets CBi2, the reflected wave is generated at this point because CBi2 is open ((1) in Figure 2). At the open end, the voltage is doubled and reflected, and the reflected wave travels again along the I feeder and meets the tie switch where the feeder with different characteristic impedances are connected, as shown in Figure 2. At this point, the refracted waveforms travel along each feeder ((2) in Figure 2).

In Figure 3, the magnitude of the voltage that is refracted at the point where the tie switch is connected is presented in Equation (1).

$$V_{f1}=\frac{2\left(Z_{ik+1}//Z_{jk}//Z_{jk+1}\right)}{Z_{ik}+\left(Z_{ik+1}//Z_{jk}//Z_{jk+1}\right)}2V$$

(1)

The refracted wave in Equation (1) can reach CBjk. In the case of an MG, because the line is short, the refraction/reflection of the traveling wave occurs frequently; hence, a surge waveform of high frequency will be generated. In this case, the reflected wave is doubled at the open end, and the duration of the switching surge having a high frequency will be longer.

3.2. Case of Failure of Fault Section Separation (Fault Current Injection from J feeder)

In a failed fault Section separation, a traveling wave occurs at the point where the tie switch is closed, as describe in Section 3.1. The traveling wave propagates along the I feeder and the reflected wave is generated at the fault point ((1) in Figure 4). The magnitude of the reflected wave is given by Equation (2).

$$V_r=\frac{R_f-Z_{if}}{R_f+Z_{if}}V$$

(2)

where $R_f$ is the fault resistance and $Z_{if}$ is the characteristic impedance of the faulted line.

As shown in Equation (2), the magnitude of the reflected wave depends on the magnitude of the fault resistance. Reflected waves are developed at the point where the tie switch is connected. At this point, the refracted waveforms travel along each feeder ((2) in Figure 4).

The circuit diagram at the connection point of the tie switch is shown in Figure 5. In Figure 5, the magnitude of the refraction wave reaching CBjk is given by Equation (3). In this case, because the line length of the MG is short, the refraction/reflection of the traveling wave occurs frequently; hence, a surge waveform of high frequency will be generated.

$$V_{f2}=\frac{2\left(Z_{ik+1}//Z_{jk}//Z_{jk+1}\right)}{Z_{ik}+\left(Z_{ik+1}//Z_{jk}//Z_{jk+1}\right)}·\frac{R_f-Z_{if}}{R_f+Z_{if}}V$$

(3)

3.3. Case of Fault in the J Feeder (Faults in the Original Feeder)

Figure 6 shows the path of the traveling wave when a fault occurs in the J feeder. When a fault occurs, the reflected wave is generated at the fault point. The magnitude of the reflected wave is given by Equation (4). The magnitude of the reflected wave is determined by the fault resistance.

$$V_r=\frac{R_f-Z_{jf}}{R_f+Z_{jf}}V$$

(4)

where $R_f$ is the fault resistance and $Z_{if}$ is the characteristic impedance of the faulted line

3.4. Comparison of Each Case

For the three cases above, the switching surge in CBjk is derived as Equations (1), (3), and (4). It is necessary to compare the magnitudes of these.

First, the difference between Equations (1) and (3) is given by Equation (5).

$$V_{\left(1\right)-\left(3\right)}=\frac{2\left(Z_{ik+1}//Z_{jk}//Z_{jk+1}\right)}{Z_{ik}+\left(Z_{ik+1}//Z_{jk}//Z_{jk+1}\right)}V\left(2-\frac{R_f-Z_{if}}{R_f+Z_{if}}\right)$$

(5)

The sign of Equation (5) is determined by $\left(2-\frac{R_f-Z_{if}}{R_f+Z_{if}}\right)$. Even though $R_f$ is larger than $Z_{if}$, $\frac{R_f-Z_{if}}{R_f+Z_{if}}$ cannot be larger than 2. Therefore, $2-\frac{R_f-Z_{if}}{R_f+Z_{if}}>0$ is always satisfied, and Equation (5) is larger than 0. In other words, Equation (1) is always larger than Equation (3).

Next, the difference between Equations (3) and (4) is given by Equation (6).

$$V_{\left(3\right)-\left(4\right)}=\frac{R_f-Z_{if}}{R_f+Z_{if}}V\left(\frac{2\left(Z_{ik+1}//Z_{jk}//Z_{jk+1}\right)}{Z_{ik}+\left(Z_{ik+1}//Z_{jk}//Z_{jk+1}\right)}-1\right)$$

(6)

In Equation (6), we examine $\frac{R_f-Z_{if}}{R_f+Z_{if}}$. The sign of this value is determined by the fault resistance $R_f$. Even if this value is smaller than 0, the absolute value is important when analyzing the magnitude of the surge. In addition, because this value is a common part of Equations (3) and (4), it cannot directly affect the magnitude comparison of Equations (3) and (4). Next, we discuss $\frac{2\left(Z_{ik+1}//Z_{jk}//Z_{jk+1}\right)}{Z_{ik}+\left(Z_{ik+1}//Z_{jk}//Z_{jk+1}\right)}-1$. To obtain a value above 0, $Z_{ik+1}//Z_{jk}//Z_{jk+1}$ should be larger than $Z_{ik}$. However, the characteristic impedance of the distribution line is similar, and $Z_{ik+1}//Z_{jk}//Z_{jk+1}$ is always smaller than $Z_{ik}$. Therefore, $\frac{2\left(Z_{ik+1}//Z_{jk}//Z_{jk+1}\right)}{Z_{ik}+\left(Z_{ik+1}//Z_{jk}//Z_{jk+1}\right)}-1$ is smaller than 0; hence, Equation (4) is always larger than Equation (3). From the discussion above, the magnitude of Equation (3) is always the smallest among the three cases.

To compare the magnitudes of Equations (1) and (4), the difference between Equations (1) and (4) is given by Equation (7). The sign of Equation (7) depends on the fault resistance. Because the magnitude of the fault resistance is unpredictable, it is impossible to compare the magnitudes of Equations (1) and (4).

$$V_{\left(1\right)-\left(4\right)}=V\left(\frac{2\left(Z_{ik+1}//Z_{jk}//Z_{jk+1}\right)}{Z_{ik}+\left(Z_{ik+1}//Z_{jk}//Z_{jk+1}\right)}-\frac{R_f-Z_{if}}{R_f+Z_{if}}\right)$$

(7)

Next, we compare the durations of the switching surge. The duration of the switching surge can be determined by the line resistance and the magnitude of the reflected wave. Because the distribution line is short, it is assumed that the decay by the line resistance is similar for all three cases. Subsequently, the duration of the switching surge can be determined by the magnitude of the reflected wave. Among the three cases, the doubled reflected wave appears only in the case of Section 3.1. In the cases presented in Section 3.2 and Section 3.3, the magnitudes of the reflected waves can be varied depending on the magnitude of the fault resistance. However, they cannot be greater than the doubled reflected wave in Section 3.1. Therefore, in a normal load current supply as presented in Section 3.1, the duration of the switching surge will be the longest. The durations of switching surge for the remaining two cases will be similar.

The results above are summarized as follows:

(1)

When a fault Section separation fails, the smallest surge waveform will appear in CBjk. The other two cases will be determined by the fault resistance.

(2)

In the case of a normal load current supply, the switching surge duration is the longest. The other two cases are similar.

4. Fault Classification Using Wavelet Transform

4.1. Fault Classification Using Wavelet Transform

To prevent the maloperation of the protection relay in the open-loop MG and to reduce the outage area, three cases should be distinguished: (1) normal load current supply (fault Section is successfully separated); (2) fault current injection to another feeder (fault Section is unsuccessfully separated); (3) fault in the original feeder. The common characteristic of the three cases is that the high-frequency waveform is included owing to the switching surge. The differences are the magnitude and duration of the switching surge. Therefore, in this study, we use the WT that can use both time and frequency components to distinguish the three cases.

The WT is decomposed into a detailed component and an approximation component. The detailed component contains the high-frequency component and the approximation contains the low-frequency component. The approximation can be resolved many times with detail and approximation. That is, at higher resolutions, the lower-frequency components are extracted [17,18]. In this study, to utilize the feature of the switching surge with high frequency, we utilize the coefficient of the detailed component of level 2 (d2). The new index to classify the three cases above is proposed in Equation (8). In this new index, the absolute value of d2 is a summation for one period.

$$NewIndex={\displaystyle \sum }_{n=k}^{k+n_{1cycles}}\left|d2\left(t\right)\right|$$

(8)

where k is present sample, and n1cycles is sample number for one period.

In the case of a normal load current supply, the duration of the switching surge is the longest; therefore, d2 will appear longer than the other cases. Therefore, the value of Equation (8) will be the largest. When the fault Section separation fails, the magnitude of the switching surge is the smallest and the duration is short; therefore, the value of Equation (8) will be the smallest. When the faults on the original feeder occur, the duration is short, but the magnitude of the switching surge is larger than that of when the fault Section separation fails. Therefore, the value of Equation (8) will appear in the middle of the two cases.

4.2. Selection of Mother Wavelet

Several types of mother wavelet (MW) exist, including Haar, Daubechies (db) N, Symlets N, Biorthogonal N, and Coiflets N. MWs can be classified according to their length and characteristics [17,18,19]. Furthermore, because the wavelets used in signal analysis can be obtained by scaling and shifting the MW, the selection of the MW is extremely important.

To select the MW, simulations are performed on the MG model, as shown in Figure 7 [1]. This MG has very short line length and small number of loads. The fault occurs at 102 Sections in the I feeder and 206 Sections in the J feeder. The fault resistance is 1 Ω, and the fault type is a single line to the ground (SLG) fault. In the case of the I feeder, the fault occurs at 0.1 s and the fault Section is determined at 0.15 s. The tie switch is subsequently closed at 0.2 s. For the J feeder, a fault occurs in 0.2 s. We used the electromagnetic transient program (EMTP) to extract the voltage waveform after system modeling and MATLAB to perform wavelet transform [18,23,24,25]. We extracted 120 samples per cycle when extracting the voltage waveform from EMTP. In this paper, EMTP/ATPDraw (developed by Hans Kr. Høidalen, Norway) was used for modeling the system model. The EMTP is a tool used to simulate transient electromagnetic phenomena, and it is one of the most widely used programs throughout electric utilities. ATPDraw is a graphical, mouse-driven pre-processor to the Alternative Transients Program (ATP) version of EMTP. MODELS in ATP is a general-purpose description language supported by an extensive set of simulation tools for the representation and study of time-variant systems. MODELS provides the monitoring and controllability of power systems, as well as some other algebraic and relational operations for programming [26,27].

Figure 8 shows the enlarged voltage waveforms measured at the front of the 206 Section, which is the tie switch connection point in the J feeder for each case. In Figure 8, “fault1” implies the case of fault current injection from the J feeder by an unsuccessful fault Section separation. Furthermore, “fault2” implies the fault at fault2 in the J feeder; “normal” implies the case of a normal load current supply from the J feeder by a successful fault Section separation. In the “normal” waveform, the duration of the switching surge is the longest, as analyzed in Section 3. The magnitude of the switching surge is the smallest in “fault 1.” Because the fault resistance is 1 Ω, “fault1” and “fault2” should be compared with each other considering Equations (3) and (4) with negative values. The WT is performed using the original voltage waveform to obtain the new index value of Equation (8).

The results of Haar, db4, and sym5, which are the most typically used MWs for power system signal analysis, are compared. Figure 9, Figure 10 and Figure 11 show the calculation result of the new index using Haar, db4, and sym5, respectively. We compare the maximum value and the time required to reach the maximum value. The comparison results are shown in

Table 1. Comparison results of MWs.

	Case	Fault 1	Fault 2	Normal
MW
Haar	Maximum value	35,000	40,000	127,000
	Time	0.0165	0.0165	0.0165
Db4	Maximum value	9200	12,300	33,000
	Time	0.0022	0.004	0.015
Sym5	Maximum value	12,900	20,300	68,200
	Time	0.0025	0.004	0.015

. In Table 1, time implies the time taken to reach the maximum value, and “fault1,” “fault2,” and “normal” are the same as those in Figure 8. From Table 1, the Haar MW exhibits the largest difference for each case among the three MWs, but requires the longest time to reach the maximum value. Therefore, the Haar MW is excluded. If we examine Db4 and sym5, it is apparent that the difference between the maximum values at each case is greater than 3000. In our comparison, the time required to reach the maximum value is highly similar; however, db4 is faster than sym 5 in the case of fault1. Therefore, we selected db4 as the MW in this study.

5. New Protection Scheme Based on Coordination with Tie Switch in an Open-Loop MG

Herein, we propose a new protection scheme based on the cooperation with a tie switch to solve the problem analyzed in Section 2. The system configuration for the proposed protection scheme is shown in Figure 12. In the conventional distribution system, over current relay (OCR) is used; therefore, only current is used to detect a fault occurrence. However, the proposed protection scheme receives voltages and currents as inputs. The protective relay subsequently issues a trip command to the tie switch and circuit breaker (CB).

Figure 13 shows the flowchart of the new protection scheme. First, the voltage and current are input to the protection relay, and WT is performed using the voltage, and the root mean square (rms) value of the current is calculated. The mother wavelet (MW) in the WT is the db4 determined in Section 4.2. Next, the proposed scheme calculates the new index proposed in Section 4.1.

If the new index is greater than β, 1 is added to judge_n to determine the normal load current supply. If the new index value is continuously greater than β during the predetermined number of samples, that is, if judge_n is greater than t_n, it is determined as the normal load current supply and the protection relay operation is blocked. If the new index is smaller than β, it is determined whether the new index is smaller than α and the rms value is larger than the trip current (Itrip). In this case, 1 is added to judge_f1 to judge the failure of the fault Section separation when a fault has occurred at the other feeder. If judge_f1 is greater than t_f1, it is judged as a failure of the fault Section separation and the open command of the tie switch is issued. If the new index is larger than α and smaller than β, and the rms value is larger than the trip current (Itrip), 1 is added to judge_f2 to judge the fault in the original feeder. If judge_f2 is greater than t_f2, it is finally judged as a fault in the original feeder. In this case, the breaker trip command according to the instantaneous or time-inverse trip is issued. In other words, the protection relay should operate normally.

In Figure 13, α is a threshold for judging the failure of the fault Section separation when the fault has occurred at other feeder, and β is a threshold for judging the normal load current supply by the successful fault Section separation when the fault has occurred at other feeder. The settings of α and β are very important to detect the fault using proposed method. These values may vary depending on the system configuration such as line length, characteristic impedance, etc. These values can be empirically determined by various simulations. t_n is the minimum number of samples to determine the normal load current supply, t_f1 is the minimum number of samples to judge the failure of the fault Section separation, and t_f2 is the minimum number of samples to judge the fault at the original MG. These three values can be a specific value, regardless of the system condition.

In the normal load current supply, the overcurrent relay in the conventional distribution system will operate if the current is larger than trip current. However, because a fault does not occur, we assumed this operation as maloperation. The proposed algorithm includes trip condition of Irms > Itrip at overcurrent relay. In other words, the proposed algorithm can have the conventional function of overcurrent relay, as well as blocking function of relay operation or tie switch operation function to prevent the maloperation of overcurrent relay.

6. Simulations

6.1. System Model and Simulation Condition

The MG model in Figure 7 was used to verify the new protection scheme proposed in Figure 13. The simulation conditions are presented in

Table 2. Simulation conditions.

Case	Fault Section	Success/Failure of Fault Section Separation
Case1	102	Success
Case2	102	Failure
Case3	105	Success
Case4	105	Failure
Case 5	206	-

. When another feeder is faulty, the fault points are set as 102 sections (long distance from the tie switch) and 105 sections (short distance from the tie switch). In each case, the success/failure of the fault section separation were simulated. When the original feeder is faulty, the fault point is set as 206 Sections near the tie switch. The fault type is an SLG fault, which is most common fault in an MG, and the fault resistance is set to 1 Ω. In cases 1–4, the fault occurred at 0.1 s, the circuit breaker was opened at 0.15 s, and the tie switch was operated at 0.2 s. In case 5, the tie switch did not function and the fault occurred at 0.2 s. In each simulation, the breaker operation after the trip command was set to be completed after three cycles.

The system was modeled by using EMTP and the voltage and current waveforms were extracted, and the proposed scheme was implemented using Matlab. We extracted 120 samples per cycle when extracting the current and voltage waveform from EMTP. In the simulation, α was set as 10,000 and β was set as 13,000. t_n, t_f1, and t_f2 were set as 30 samples. That is, the minimum duration to determine each case was set to 1/4 cycles.

6.2. Simulation Results

For each case, the calculation results of the new index, the trip command, and the current waveform in the J feeder are shown. In the trip command, “3” implies the blocking command, “2” implies the tie switch open command, and “1” implies the CB open command.

Figure 14 shows the simulation results of cases 1 and 2. Figure 14a shows the calculation results of the new index in cases 1 and 2. In case 1, the tie switch operates at 0.2 s and the new index is increased to 33,000, which is greater than β. However, in case 2, the new index having the maximum value of 9200 does not increase beyond α value after the tie switch is closed in 0.2 s. Therefore, according to the proposed protection scheme, case 1 issues a blocking command “3” at 0.2063 s and case 2 issues a tie switch open command “2” at 0.2061 s, as shown in Figure 14b. In Figure 14c, after the tie switch is closed at 0.2 s, the current flow is more than double. However, in this case, it is judged as the normal load current supply and the blocking signal is generated. Hence, the normal load current is supplied continuously from the J feeder to the I feeder. In Figure 14d, after the tie switch is closed at 0.2 s, a large fault current is observed. However, after the tie switch open command is issued at 0.2061 s, the normal load current in the J feeder flows again after 0.2561 s considering the CB operating time of three cycles.

Figure 15 shows the results of cases 3 and 4. In this case, the fault point is closer to the tie switch than in cases 1 and 2. As shown in Figure 15a, after the tie switch is closed at 0.2 s, the new index in case 3 is increased above the setting value β, while that in case 4 is not increased above the setting value α. Therefore, as shown in Figure 15b, a blocking command in case 3 is issued in 0.2086 s and a tie switch open command in case 4 is issued in 0.2056 s. As shown in Figure 15c, the 47 [A] before the tie switch close is increased 2.4 times to 113 [A] after the tie switch closes. In the conventional OCR, the instantaneous trip condition is satisfied. However, according to the protection scheme proposed herein, because the protection relay outputs a blocking signal, the normal load current is therefore supplied continuously. In Figure 15d, the fault current is injected after the tie switch is closed, and the fault current is much larger than the normal load current. Therefore, according to the protection scheme, the protection relay issues a tie switch open command, and the tie switch is completely closed at 0.2556 s considering the operation time. Therefore, thereafter, a normal load current flows again.

Figure 16 shows the simulation results of case 5. As shown in Figure 16a, the new index value after the fault occurrence indicates the intermediate value between α and β as 12,300. As shown in Figure 16c, the fault current is 2.6 times higher than the normal current. Therefore, as shown in Figure 16b, the circuit breaker open command is issued at 0.205 s. As shown in Figure 16c, the current is cut off after 0.255 s after the completion of the circuit breaker operation.

6.3. Comparison with Previous Works

To prove the superiority of the proposed protection scheme, we compare the results using the protection method in previous studies. In each figure, “proposed” implies the result of applying the proposed protection scheme, “conventional” implies the result of applying the conventional OCR, and “ref1” implies the result of applying the algorithm in reference [1]. Here, only the current at phase A is compared.

Figure 17 shows the comparison result of case 1. Before 0.256 s, the results of the proposed scheme and those of previous studies are the same. However, when conventional OCR is applied, it is recognized as a fault because the current exceeds 2.5 times the normal current and the CB is opened. That is, when conventional OCR is applied, the load experiences an outage. However, in the case of the proposed scheme and ref1, the normal current flows because the operation of the protection relay is blocked.

Figure 18 shows the comparison result of case 2. Case 2 is a case of failed fault Section separation; therefore, the large fault currents of all methods flow. In the proposed scheme, the tie switch is closed at 0.2561 s, such that the normal load current flows again in the J feeder, as shown in Figure 18b. However, the results of “conventional” and “ref1” are that the breaker in the J feeder instead of tie switch is opened; therefore, the current becomes zero even though the J feeder is not faulty. That is, if the proposed method is applied, the load does not experience an outage; however, if the conventional OCR and the method in “ref1” are applied, the load experiences an outage.

Figure 19 shows the comparison result of case 3. The result is highly similar to that of case 1 in Figure 17. In this case, the proposed method and the “ref1” method can supply a normal load current. However, in the conventional OCR, the current flows twice or more and hence the current is cut-off.

Figure 20 shows the comparison result of case 4. This case is highly similar with case 2. In the “conventional” and “ref1” cases, the CB in the J feeder is opened because it is judged as a fault. After 0.256 s, the current becomes zero, and the remaining loads in the J feeder experience an outage. However, in the proposed method, the tie switch is opened because it is judged as a fault in the I feeder. Therefore, the normal load current flows back in the J feeder, as shown in Figure 20b, and the load does not experience an outage.

Figure 21 shows the comparison result of case 5. In this case, all three methods detect the fault and the current is cut-off.

6.4. Discussions

The MG model in Figure 7 has the characteristics of a typical MG model with a short length. In this paper, the loop MG was constructed by connecting the same two feeders with the tie switch. When the traveling wave generated by the fault in the other feeder propagates to the original feeder, it firstly meets the tie switch and the CB with protection relay. In the proposed system, the protective relay is installed in the CB closest to the tie switch to control the circuit breaker and the tie switch. Therefore, the factor that has the greatest influence on the proposed method is the characteristics of the other feeder in which the fault occurs. That is, although the configuration of the two feeders in Figure 7 is the same, it does not affect to the performance of the proposed protection method.

In this paper, the simulation results according to fault section, success/failure of fault Section separation, are discussed. These are the factors that have the greatest influence on the new index. The faults simulated are the SLG fault with the fault resistance of 1 Ω. The SLG faults are very frequent faults in the MG. Because the analysis in the Section 3 is based on the SLG fault, the proposed method accurately operates in the SLG fault. As a future study, we will develop the algorithm considering all fault types.

We simulated various fault resistances. When the high impedance faults above 100 Ω occurred, the fault classification using α and β values in Section 6.1 failed. In this case, α and β should be changed. The proposed protection scheme using the new index was based the fault characteristic by traveling wave. In particular, the magnitude of the reflected wave was significantly affected by the fault resistance. In addition, in high fault resistance, the reflected wave may be extremely small if the characteristic impedance of the line is similar to the fault resistance. In other words, when the fault resistance is large, it affects to the new index value, so the setting of α and β values should be changed. In this paper, α and β values for the simulation are suitable for low impedance faults. As a future research, we will develop a protection method for the loop MG regardless of the fault resistance.

7. Conclusions

The conventional distribution system is a radial distribution system. However, owing to the increase in load and the reliability of the power supply, the loop-type distribution system such as an MG is increasing. A loop MG is capable of bidirectional power supply; therefore, the maloperation of the protection relay may occur. Herein, we proposed a solution to this problem.

The considerations for protection in the loop MG were analyzed, and the possibility of a maloperation was also analyzed. To develop countermeasures against a maloperation, the characteristics of the fault currents were analyzed. Using the analyzed characteristics, we developed a new index to distinguish the fault at other feeder, the normal load current supply to other feeder, and the fault at the original feeder. We developed a new protection scheme based on the coordination with a tie switch using proposed new index. The proposed method could accurately distinguish the fault at another feeder, the normal load current supply to another feeder, and the fault at the original feeder.

To verify the proposed method, the MG model was modeled using the EMTP, and the proposed method was implemented using MATLAB. Various simulations according to the fault location and the success/failure of the fault Section separation were performed and compared with previous research results. From the simulation results of previous studies, it was confirmed that the loads on the MG experienced an outage because the circuit breaker of the line was opened even though the fault had occurred at the other feeder. However, in the proposed protection scheme, the blocking signal was issued accurately in the normal load current supply case. Furthermore, the fault at the other feeder was judged accurately; hence, the tie switch open command was issued. It was found that no outage occurred in the other feeder.

We do not consider overvoltage due to switching off power switch, power switch duty time, arc eliminated methods, constantly changing impedances of the consumers, and thus also for powerlines. Therefore, we will consider them as future study.