A Study on the Out-of-Step Detection Algorithm Using Time Variation of Complex Power-Part II: Out-of-Step Detection Algorithm and Simulation Results

Abstract

One of the established unstable power swing (out-of-step) detection algorithms in micro grid/smart grid power systems uses a trajectory of apparent impedance in the R-X plane. However, this algorithm is not suitable for fast out-of-step conditions and it is hard to detect out-of-step conditions exactly. Another algorithm for out-of-step detection is using phasor measurement units (PMUs). However, PMUs need extra equipment. This paper presents the out-of-step detection algorithm using the trajectory of complex power. The trajectory of complex power and generator mechanical power is used to identify out-of-step conditions. A second order low pass digital filter is used to extract the generator mechanical power from the complex power. Variations of complex power are used to identify equilibrium points between stable and unstable conditions. The proposed out-of-step algorithm is based on the modification of assessment of a transient stability using equal area criterion (EAC). The proposed out-of-step algorithm is verified and tested by using alternative transient program/electromagnetic transient program (ATP/EMTP) MODELS.

1. Introduction

The trajectory of apparent impedance has been used to detect out-of-step conditions like micro grid/smart grids in power systems. However, a fast out-of-step condition may pass the out-of-step detection zone very fast, so it is hard to detect fast out-of-step conditions and one cannot detect out-of-step conditions exactly. Another out-of-step detection algorithm is using a phasor measurement unit (PMU) [1,2,3,4]. By measuring a phasor designed at a relay, a PMU can estimate the generator angle directly. However, to use PMU a Global Positioning System (GPS) is necessary. From all the above cases, it becomes apparent that a new out-of-step detection algorithm is needed which should consider transient stability in power systems.

This paper describes the new out-of-step detection algorithm which uses the trajectory of complex power and generator mechanical power. The generator mechanical power is extracted from the reactive power. Transient stability is estimated by complex power and mechanical power with complex power mathematical model which was mentioned in Part I. The new out-of-step detection algorithm which is described this paper could replace conventional out-of-step detection algorithms and it is faster and more accurate. The proposed algorithm is verified and tested by ATP/EMTP MODELS.

2. Conventional Out-of-Step Detection Algorithms

The distance relay uses apparent impedance to detect power swing conditions in the R-X plane, but when a power swing occurs, the apparent impedance trajectory is similar to a fault condition, so every case which uses apparent impedance to identify power swing conditions has to focus on distinguishing between faults and power swings. When a fault occurs in a power system, the apparent impedance converges on the fault detection zone fast. Likewise, if a power swing occurs in a power system, the apparent impedance converges on the fault detection zone.

However, when a power swing occurs, the convergence speed of the apparent impedance is slower than under fault conditions, so the convergence speed can be a reference to discriminate between faults and power swing [5,6,7]. Power swings and faults in power systems may disturb the power supply and cause damage in micro grid/smart grid power systems. From such a view point, these systems must be protected from power swings and faults. To do so power swings should generally, be blocked and faults should be tripped.

2.1. Out-of-Step Detection Algorithm Using a Single Blinder in R-X Plane

Figure 1 shows out-of-step detection algorithm using a single blinder in the R-X plane. Each blinder is located on both sides of 100% of the line impedance. When an out-of-step condition occurs, the convergence speed of the apparent impedance is slower than that of a fault condition. Equation (1) shows the condition for detecting an unstable swing [5]:

$$\left|T2-T1\right|>T_{tripping}$$

(1)

where T1 and T2 are the blinder passing time of the apparent impedance on the R-X plane and T_tripping is the threshold time of tripping. If the passing time between T1 and T2 is larger than T_tripping, it is an unstable swing. However, this algorithm cannot distinguish between faults and stable power swings and cannot detect unstable swings until the trajectory of the apparent impedance passes T2. The generator angle can be increased [5].

2.2. Out-of-Step Detection Algorithm Using a Double Blinder in the R-X Plane

Likewise, Figure 1 and Figure 2 show out-of-step detection algorithms using the apparent impedance in the R-X plane. Different from the previous algorithm, it uses a double blinder instead of a single blinder and it can identify stable swings. The power swing detection element “dZ” in Figure 2 is used as a reference of identification which distinguishes between stable swings and unstable swings.

Referring to Equation (2), faults and power swings can be identified by:

$$T_{dZ}<T_{PSB}$$

(2)

where T_dZ: Passing time of apparent impedance and T_PSB: Threshold time of power swing blocking.

Power swing and faults can be identified by the speed of the apparent impedance which passes through the power swing detection element. Stable swings and unstable swings can also be identified by dZ. If an unstable swing occurs, the trajectory of the apparent impedance would pass from right dZ to left dZ (left dZ is the left side of Zone 1 and right dZ is the right side of Zone 1) [5,6,7]. However, if a stable swing occurs in the power system, the trajectory of apparent power will curve instead of passing left dZ. This algorithm also has to wait until the trajectory of the apparent impedance passes the left side dZ to identify an unstable swing.

2.3. Out-of-Step Detection Algorithm Using a Concentric Circle Type in the R-X Plane

The concentric circle type which uses Mho characteristics in a distance relay could be used to detect out-of-step conditions. Figure 3 shows how to detect unstable and stable swings in the R-X plane. It has the ability to detect the trajectory of apparent impedance from above or below. It also uses the apparent impedance, but this algorithm also has to wait until the trajectory of the apparent impedance has passed the left side dZ to identify unstable swings [5,6,7].

2.4. Out-of-Step Detection Algorithm Using Phasor Measurement Unit (PMU)

Unlike the previous methods, a PMU takes data from a local relay to extract the phase angle directly. Figure 4 shows data synchronization using a Global Positioning System (GPS) between two local relays. This synchronized data is then sent to a central control center (CCC) to estimate the generator angle. By using this generator angle which is estimated from data, local relays can trip faults that cause unstable swings. Because the PMU uses the generator angle instead of the trajectory of apparent impedance, it is more exact than the previous methods described in Section 2.1 and Section 2.2 However, a PMU needs extra equipment. In addition, from a utility’s point of view, it is best to perform the same role using an existing device without installing additional equipment. Installation of new devices can increase the complexity of the system, which is not preferred by operators. For example, it is possible to quickly share information using communication technology, but there is also another problem of installing communication systems for sharing information and paying attention to security. At this point, the new out-of-step detection algorithm that is more exact than upper the algorithm, faster than Section 2.1 and Section 2.2 in the R-X plane and is low-cost (no extra equipment is needed) is required.

3. Novel Out-of-Step Detection Algorithm

3.1. Transient Stability Using Complex Power Variations

Figure 5 shows the trajectory of complex power on the complex power plane which is presented in Part Ι. As mentioned before in Part Ι, the trajectory of complex power will be moved in line with an ellipse. Mechanical power is the input power of a generator [8,9,10,11]. The point which is (0, α) is the horizontal axis of ellipse will have a 90° generator angle. This can be defined as follows:

$$Q=j\left\{\frac{\left|X_S\right|\left|E_R\right|\left|E_S\right|\cos \delta -\left|X_L\right|\left|E_R\right|\left|E_S\right|\cos \delta +\left|X_L\right|{\left|E_S\right|}^2-\left|X_S\right|{\left|E_R\right|}^2}{{(X_S+X_L)}^2}\right\}$$

(3)

The reactive power Equation (3) could be written more simply as follows:

$$Q=j\left\{\frac{\left|X_S\right|\left|E_R\right|\left|E_S\right|-\left|X_L\right|\left|E_R\right|\left|E_S\right|}{{(X_S+X_L)}^2}\right\}\cos \delta +j\left\{\frac{\left|X_L\right|{\left|E_S\right|}^2-\left|X_S\right|{\left|E_R\right|}^2}{{(X_S+X_L)}^2}\right\}$$

(4)

If the generator angle δ is 90 degrees, then Equation (4) is written as:

$$Q=j\left\{\frac{\left|X_L\right|{\left|E_S\right|}^2-\left|X_S\right|{\left|E_R\right|}^2}{{(X_S+X_L)}^2}\right\}=\alpha$$

(5)

If the power system is stable, the mechanical power and electrical power will be same at the stable equilibrium point (SEP) [8,9,10,11]. When faults occur in a power system, the trajectory of complex power will be swinging and may pass an unstable equilibrium point (UEP), i.e., the point at which the equilibrium collapses as the generator’s angle increases by 90°, then the power system will be in an unstable swing condition (out-of-step condition).

3.2. Mechnical Power Estimation from Electrical Power

To determine SEP or UEP, a reference is needed. At this point, mechanical power can be used to determine stable or unstable conditions. If the mechanical power and electrical power are the same with a generator angle over 90°, it will be an unstable condition [8,9,10,11]. Otherwise, an generator angle below 90°, indicates a stable condition.

However, it is not easy to take generator angle data directly from generators, so another way to take generator angles is needed. As mentioned before, mechanical power and electrical power are the same at a SEP. This means that the mechanical power can be estimated from the electrical power at the SEP. There are two ways to estimate mechanical power from electrical power. One is using electrical power data before a power swing. Another is mechanical power estimation from electrical power using a low-pass filter. This paper uses mechanical power data estimation from electrical power using a second order Butterworth low-pass filter, as shown in Figure 6.

Figure 6 shows how to estimate the mechanical power from the electrical power using a second order low-pass filter. To estimate mechanical power from electrical power, the cut-off frequency of the low-pass filter must be determined. This cut-off frequency can be determined using frequency spectrum analysis in the frequency domain.

Figure 7 shows a spectrum analysis of electrical power in the frequency domain to determine the low-pass filter cut-off frequency. Before the power swing condition, electrical power which contains only a DC component in the frequency domain operates in a steady state. Therefore, the cut-off frequency has to determine how to extract this DC component in the frequency domain. In order to identify the cut-off frequency of the low-pass filter, simulation studies have been conducted on various events, such as line length variations and different fault locations.

Table 1. Simulation results to identify the cut-off frequency of low-pass filter.

Fault Clearing time	10 cycle	20 cycle	30 cycle
Cut-off Frequency	0.1 Hz	0.1 Hz	0.1 Hz
Line Length	100 km	200 km	300 km
Cut-off Frequency	0.1 Hz	0.1 Hz	0.1 Hz
Fault Distance	Fault Distance of 10%	Fault Distance of 50%	Fault Distance of 90%
Cut-off Frequency	0.1 Hz	0.1 Hz	0.1 Hz

shows that the simulation result of the cut-off frequency is 0.1 Hz and this is used to estimate the mechanical power from electrical power in this paper. Based on various simulations that were performed, the cut-off frequency was 0.1 Hz when considering the implementation of the filter for relay and ATP/EMTP simulation.

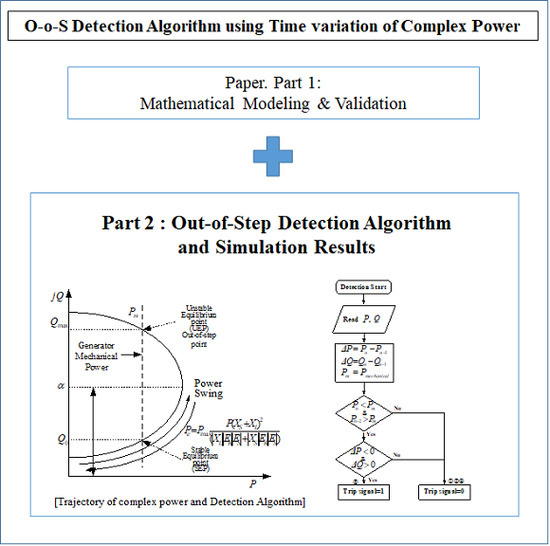
3.3. Out-of-Step Detection Algorithm Using a Trajectory of Complex Power

Figure 8 shows the out-of-step detection algorithm using a time variation of complex power. There are two points Q_max and Q₀. Q_max is the reactive power of UEP and Q₀ is the reactive power of SEP. Based on the Part I, the equilibrium points can classify Q_max and Q₀ by α, which is the horizontal axis of the complex power ellipse. However, as shown in Equation (5), if α is used to classify equilibrium points, line data and source data (each side) are needed to solve Equation (5), thus another method is needed, so instead of reference α, the time variation of complex power with the equilibrium point is used to identify out-of-step condition. Figure 8 shows how to classify four cases which are shown in Figure 8.

Figure 9 shows four cases for classification of complex power with time variation. The variation of complex power $\frac{\Delta P}{\Delta t}$ and $\frac{\Delta Q}{\Delta t}$ are used to classify each case. By using this, the state of the power system (unstable swing or stable swing) can be identified and out-of-step conditions can be detected.

As shown above, ① and ② are stable swings and ③ and ④ are unstable swing conditions. The final goal of this paper is a new out-of-step detection algorithm, so stable swing will not be discussed. Case ④ is an unstable swing after out-of-step condition, so it will also not be discussed.

Figure 10 shows the novel out-of-step detection algorithm using the time variation of complex power, where ΔP is the time variation of active power and ΔQ is the time variation of reactive power. The trip signal is activated when the mechanical power P_m is in the middle of the electrical power P_n and P_n-2 which are two samples before P_n with a time variation ΔP smaller than 0 and ΔQ is larger than 0. This algorithm consists of two steps. In the first, we find out the equilibrium point and second, we identify the unstable equilibrium point. Equation (6) shows how to find the equilibrium point:

$$P_{n-2}<P_m<P_n$$

(6)

where P_n-2 is the active power value of the two samples mentioned before, P_n is the current active power and P_m is the mechanical power. There are only two points which satisfy this condition: SEP and UEP, thus how to find out the unstable equilibrium point is needed.

Table 2. Classification between SEP and UEP using time variation of complex power.

State	Number	ΔP	ΔQ
SEP	①	+	+
	②	−	+
UEP	③	−	−
	④	+	−

shows four cases to find out unstable equilibrium points.

Table 2 can be used to identify four cases which are the trajectories of complex power on a complex power plane. The concept of ‘new out-of-step detection algorithm’ is the classification of the equilibrium using the time variation of complex power.

4. Simulation Results

4.1. Simulation Method

A set of simulation tests were carried in a test model of a power system shown in Figure 11 which is interfaced with a model of a relay implemented using the ATP/EMTP MODELS software. This simulation is performed to prove the new out-of-step algorithm which uses the time variation of complex power in power systems.

To show the advantage of our new out-of-step detection algorithm, an out-of-step detection simulation which uses a single binder in the R-X plane was conducted under the same conditions. Three phase faults occurred at the distance of 50% of the transmission line and the initial generator angle is 30°. The transmission system model comprises of a total line length of 100 km; the nominal power frequency is 60 Hz. A synchronous machine (SM) card and TACS are used for the governor and excitation system of “A” nuclear power plant in Korea [12,13,14,15].

4.2. Three Phase Fault: Clearing after 10 Cycles

The novel out-of-step detection adopting the algorithm of Figure 10 is simulated. The considered fault is a 3-phase fault, which occurs 1 s after the start of the simulation. In the simulation of the new out-of-step detection algorithm, Figure 12 depicts the active, reactive and mechanical power waveforms when the out-of-step condition has occurred after fault clearing. In Figure 12, the mechanical power which is extracted from the active power is shown. In the case of a transient fault, the reactive power is increased at the out-of-step point and the active power is decreased at the same point when the out-of-step event occurred.

Figure 13 depicts the trajectory of the complex power and mechanical power on the complex power plane after a fault occurrence. Complex power in Figure 13 shows a part of the ellipse which is mentioned before in Part I of the paper. When an out-of-step condition occurs, the trajectory of the complex power moves in a counterclockwise direction until it reaches beyond 180°, and the complex power pass UEP where mechanical power and electrical power are equal.

When the initial generator angle is 30°, the generator angle after the three-phase fault is shown in Figure 14. Here, the fault is cleared 10 cycles after the fault occurred. As seen in Figure 13, the angle oscillations are increased and dampen out finally after the out-of-step incident occurred. The new out-of-step detection algorithm is used to detect the out-of-step condition and a tripping signal appears where the generator angle is 127°.

4.3. Three Phase Fault: Clearing after 15 Cycles

When the fault clearing time increases from 10 cycles to 15 cycles, out-of-step conditions become serious. Figure 15 depicts the active, reactive and mechanical power waveforms after a fault has occurred. Different from above, the out-of-step condition occurred faster than in Figure 15. Also in the case of that out-of-step condition, the reactive power is increased at the out-of-step point and the active power is decreased at same point when the out-of-step incident occurred.

Figure 16 depicts the trajectory of the complex power and mechanical power on the complex power plane after a fault occurred. Different from Figure 13, the trajectory is increased which means the out-of-step condition became serious.

Figure 17 depicts first swing stable (FSS) condition which means the first time generator angle swing and divergence. Here, the fault is cleared 15 cycles after the fault had occurred. As seen in Figure 17, the angle oscillations are increased and go out finally after the out-of-step event occurred. At the moment of the out-of-step condition, the generator angle had increased to 125° and a tripping signal which uses the new out-of-step detection algorithm appeared where the generator angle is 125°.

4.4. Three Phase Fault: Clearing after 20 Cycles

This is the first swing unstable (FSU) condition. Because the fault clearing time increases, the out-of-step has occurred after the fault was cleared. As shown in Figure 18, an out-of-step condition occurred after 3 s.

Figure 19 depicts the trajectory of the complex power and mechanical power on complex power plane after the fault occurred. Like in Figure 16, the trajectory is increased which means the out-of-step condition became serious.

Figure 20 depicts the first swing unstable (FSU) condition which means a generator angle divergence after the first swing. Here, the fault is cleared at 20 cycles after the fault had occurred. As seen in Figure 20, the generator angle had gone out after the out-of-step event occurred. At the moment of the out-of-step condition, the generator angle had increased to 113.5° and a tripping signal which uses new out-of-step detection algorithm appeared where the generator angle is 113.5°.

4.5. Comparison of the New Out-of-Step Detection Algorithm with a Single Blinder Algorithm

Under the same conditions, the new out-of-step detection algorithm which uses the trajectory of the complex power and the conventional out-of-step detection algorithm which uses a single blinder in the R-X plane are compared.

Table 3. Comparisons the new out-of-step detection algorithm with a single blinder algorithm.

	Single Blinder in R-X Plane		Trajectory of Complex Power
Fault Clearing Time	Generator Angle	Tripping	Generator Angle	Tripping
10 cycle	226.2°	7.62 s	127°	7.05 s
15 cycle	222.5°	5.22 s	125°	4.61 s
20 cycle	225.6°	3.02 s	113.5°	2.04 s

shows the tripping time (out-of-step detection time) and generator angle which is the angle of the out-of-step moment.

Table 3 shows what is faster and what is more stable. The generator angle of our new out-of-step detection algorithm does not go over 180°, however the single blinder does go over. The tripping time (out-of-step detection moment) of the new out-of-step detection algorithm is faster than that of the single blinder by about 0.6 s. Therefore, in view of the transient stability and speed of detection time, the new out-of-step detection algorithm offers a further advantage.

5. Conclusions

This paper has presented the new out-of-step detection algorithm for improving the system stability. Herein, the new out-of-step detection algorithm is used in order to detect out-of-step conditions and enhance the transient stability. It uses complex power instead of apparent impedance to detect out-of-step conditions. Mechanical power, which is used to reference the equilibrium point, is extracted from the electrical power using a 2nd order Butterworth filter. Using by mechanical power and the trajectory of complex power in the complex power plane, the new out-of-step detection algorithm can detect equilibrium points which represent stable or unstable states of a power system. At the same time, the time variation of complex power is used to identify equilibrium points which are stable or unstable.

The simulation results show that the equilibrium points are classified accurately by using the mechanical power, the trajectory of complex power with time variation of complex power, and out-of-step conditions are detected by using the proposed out-of-step detection algorithm.

The new out-of-step detection algorithm presented herein is fast, accurate and does not need extra equipment such as GPS. This is an advantage of the new out-of-step detection algorithm over others. From a utility’s point of view, it is best to perform the same task on the existing system without installing additional equipment. Finally, the new out-of-step detection algorithm presented herein will also be applicable in backup protection and system protection schemes (SPSs) for protecting generators.