Novel Adsorption Cycle for High-Efficiency Adsorption Heat Pumps and Chillers: Modeling and Simulation Results
Abstract
:1. Introduction
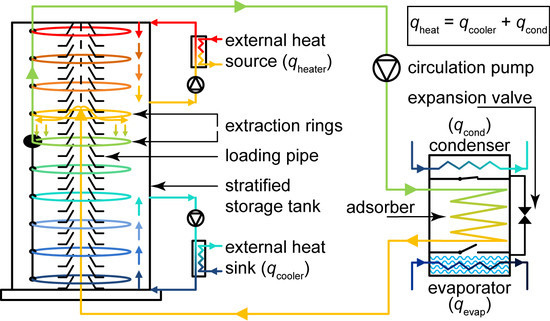
2. The Stratisorp System
2.1. Cycle Concept and Storage Integration
2.2. Adsorber Design
2.3. Heater and Cooler
3. Description of the Model
3.1. Adsorber, Evaporator, and Condenser
3.1.1. Adsorber Heat Flow
3.1.2. Effective Adsorber Thickness
3.1.3. Lateral Heat Conduction in Adsorber
3.1.4. Fluid Energy Balance in Adsorber
3.1.5. Fractional Plug Flow
3.1.6. Mass Transfer in Adsorber
3.1.7. Adsorber Chamber Energy Balance
3.1.8. Evaporator and Condenser Heat Flow
3.1.9. Evaporator and Condenser Energy Balance
3.2. Storage
3.3. Cycle Control
3.4. Simulation Details
4. Results and Discussion
4.1. Analysis of Transient Cycle Behavior
4.1.1. Adsorber Module
4.1.2. Storage Temperatures
4.1.3. Second Law Analysis
- driving temperature differences in all heat exchangers (, , , ), which are computed by integrating over time the entropy production rate [10] (Eq. 3.49)where the upper sign is valid for the adsorption and the condenser, the lower sign for desorption and evaporator, respectively,
- heat exchange with pipes and other thermal capacities like (multi-way) valves (),
- throttling of the working fluid from the condenser to the evaporator conditions (thr) [10] (Eq. 3.61),
- superheating the working fluid from the evaporator temperature to the temperature of the adsorber nodes () and desuperheating down to the condenser temperature () [10] (Eq. 3.43 and 3.55),
- heat exchange between adsorber nodes (),
- numerical dissipation in all fractional plug flows (e.g., representing the system mass flow, subscripted for the adsorber , for the storage ),
- convection and conduction in the storage (, ), computed via summing up over all time steps in adsorption or desorption half cycle the entropy production in a single time step at time [10] (Eq. 4.69)where and are temperatures of the ith storage layer at time or time , respectively,
- the heat exchange between adsorber and chamber and chamber and evaporator or condenser, which is set to zero for this paper (), and
- loading exchange between adsorber nodes (adsorbate redistribution) when the valve is closed ().
4.2. Sensitivity Analysis
4.2.1. Variation of Adsorption Module Parameters
4.2.2. Heat Transfer in the Adsorber
4.2.3. Mass Transfer between Adsorption Site and Evaporator/Condenser
4.2.4. Sensible Thermal Mass
4.2.5. Variation of Storage Volume
4.2.6. Variation of Control Parameters
- the system mass flow rate: (major influence),
- the temperature difference used for switching the half cycle: (medium influence), and
- the temperature difference used to determine : (minor influence).
4.3. Seasonal Performance
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CAD | computer-aided design | |
| HTF | heat transfer fluid | |
| LDF | linear driving force | |
| Symbols | ||
| A | area | |
| c | specific thermal capacity | |
| C | thermal capacity | |
| coefficient of performance | 1 | |
| d | diameter or length | |
| D | thickness of adsorbent | |
| h | specific enthalpy | |
| h | heat transfer coefficient | |
| h | storage height | |
| l | length scale hyperparameter of Gaussian process regression | 1 |
| l | length | |
| L | height of storage | |
| m | mass | |
| mass flow | ||
| n | number of adsorber nodes | 1 |
| Nußelt number | 1 | |
| p | pressure | |
| P | power | |
| Prandtl number | 1 | |
| q | specific heat | |
| Q | heat | |
| rate of heat flow | ||
| r | radius | |
| Reynolds number | 1 | |
| s | specific entropy per heat | |
| seasonal coefficient of performance | 1 | |
| t | time | |
| T | temperature | |
| u | specific internal energy | |
| canonical unit vector | 1 | |
| U | overall heat transfer coefficient | |
| x | loading | |
| x | length dimension along adsorbate flow | |
| X | storage constant | 1 |
| Y | storage constant | 1 |
| z | length dimension along HTF flow | |
| Z | storage constant | 1 |
| effective diffusion coefficient | = | |
| fraction (cooler, heater) | 1 | |
| effectiveness of heat exchanger | 1 | |
| splitting factor for diffusion coefficient | 1 | |
| maximum amplification of fluid thermal conductivity | 1 | |
| thermal conductivity | ||
| mean height of the amplification of the thermal conductivity | ||
| signal variance hyperparameter of Gaussian process regression | 1 | |
| noise variance hyperparameter of Gaussian process regression | 1 | |
| Amplification width of fluid thermal conductivity | ||
| Subscripts | ||
| ⊥ | orthogonal | |
| a | adsorbate | |
| ads | adsorber | |
| avg | average | |
| c | chamber | |
| cap | cap (top or bottom) | |
| cd | condenser | |
| cl | cooler | |
| cool | cool | |
| Cu | copper | |
| eff | effective | |
| end | last adsorber node | |
| env | environment | |
| ev | evaporator | |
| g | gaseous | |
| h | housing | |
| heat | heat | |
| ht | heater | |
| htf | heat transfer fluid (HTF) | |
| hx | heat exchanger | |
| in | incoming | |
| insu | insulation | |
| irr | irreversible | |
| l | (including) loss | |
| lam | laminar | |
| lq | liquid | |
| ly | storage discretization layers | |
| min | minimum | |
| out | outgoing | |
| pi | pipe | |
| pool | pool | |
| rj | reject | |
| s | adsorbent | |
| sat | saturated | |
| set | setpoint | |
| st | isosteric | |
| stor | storage | |
| wall | wall | |
References
- Ziegler, F. Sorption heat pumping technologies: Comparisons and challenges. Int. J. Refrig. 2009, 32, 566–576. [Google Scholar] [CrossRef]
- Pons, M.; Poyelle, F. Adsorptive machines with advanced cycles for heat pumping or cooling applications. Int. J. Refrig. 1999, 22, 27–37. [Google Scholar] [CrossRef]
- Ng, K.C.; Wang, X.; Lim, Y.S.; Saha, B.B.; Chakarborty, A.; Koyama, S.; Akisawa, A.; Kashiwagi, T. Experimental study on performance improvement of a four-bed adsorption chiller by using heat and mass recovery. Int. J. Heat Mass Transf. 2006, 49, 3343–3348. [Google Scholar] [CrossRef]
- Li, X.; Hou, X.; Zhang, X.; Yuan, Z. A review on development of adsorption cooling—Novel beds and advanced cycles. Energ. Convers. Manage. 2015, 94, 221–232. [Google Scholar] [CrossRef]
- Schmidt, F.P.; Füldner, G.; Schnabel, L.; Henning, H.M. Novel cycle concept for adsorption chiller with advanced heat recovery utilising a stratified storage. In Proceedings of the 2nd International Conference on Solar Air-Conditioning, Tarragona, Spain, 18–19 October 2007; OTTI: Tarragona, Spain, 2007; pp. 618–623. [Google Scholar]
- Schwamberger, V.; Glück, C.; Schmidt, F.P. Modeling and transient analysis of a novel adsorption cycle concept for solar cooling. In Proceedings of the ISES World Congress, Kassel, Germany, 28 August–2 September 2011. [Google Scholar]
- Schwamberger, V.; Glück, C.; Schmidt, F.P. A novel adsorption cycle with advanced heat recovery for high efficiency air-cooled adsorption chillers. In Proceedings of the 23rd IIR International Congress of Refrigeration (ICR), Prague, Czech Republic, 21–26 August 2011. [Google Scholar]
- Schwamberger, V.; Joshi, C.; Schmidt, F.P. Second law analysis of a novel cycle concept for adsorption heat pumps. In Proceedings of the International Sorption Heat Pump Conference ISHPC’11, Padua, Italy, 6–8 April 2011; pp. 991–998. [Google Scholar]
- Schwamberger, V.; Schmidt, F.P. Smart use of a stratified hot water storage through coupling to an adsorption heat pump cycle. In Proceedings of the 8th International Renewable Energy Storage Conference and Exhibition (IRES 2013), Berlin, Germany, 18–20 November 2013. [Google Scholar]
- Schwamberger, V. Thermodynamische und numerische Untersuchung eines neuartigen Sorptionszyklus zur Anwendung in Adsorptionswärmepumpen und -kältemaschinen. Ph.D. Thesis, Karlsruhe Institute of Technology, Karlsruhe, Germany, 2016. [Google Scholar] [CrossRef]
- Cacciola, G.; Restuccia, G. Reversible adsorption heat pump: a thermodynamic model. Int. J. Refrig. 1995, 18, 100–106. [Google Scholar] [CrossRef]
- Schicktanz, M.; Núñez, T. Modelling of an adsorption chiller for dynamic system simulation. Int. J. Refrig. 2009, 32, 588–595. [Google Scholar] [CrossRef]
- Henninger, S.K.; Schmidt, F.P.; Henning, H.M. Water adsorption characteristics of novel materials for heat transformation applications. Appl. Therm. Eng. 2010, 30, 1692–1702. [Google Scholar] [CrossRef]
- Núñez, T. Charakterisierung und Bewertung von Adsorbentien für Wärmetransformationsanwendungen. Ph.D. Thesis, Albert Ludwig University of Freiburg, Freiburg, Germany, 2001. [Google Scholar]
- Thomsen, L. Geometrieparametervariation eines Adsorberwärmetauschers für eine Adsorptionswärmepumpe; Student Research Project; Institute of Fluid Machinery, Karlsruhe Institute of Technology: Karlsruhe, Germany, 2012. [Google Scholar]
- Henninger, S.K.; Ernst, S.J.; Gordeeva, L.; Bendix, P.; Fröhlich, D.; Grekova, A.D.; Bonaccorsi, L.; Aristov, Y.; Jaenchen, J. New materials for adsorption heat transformation and storage. Renew. Energy 2017, 110, 59–68. [Google Scholar] [CrossRef]
- Aristov, Y. Concept of adsorbent optimal for adsorptive cooling/heating. Appl. Therm. Eng. 2014, 72, 166–175. [Google Scholar] [CrossRef]
- Meunier, F.; Poyelle, F.; LeVan, M.D. Second-law analysis of adsorptive refrigeration cycles: The role of thermal coupling entropy production. Appl. Therm. Eng. 1997, 17, 43–55. [Google Scholar] [CrossRef]
- Wittstadt, U.; Füldner, G.; Schnabel, L.; Schmidt, F.P. Comparison of the heat transfer characteristics of two adsorption heat exchanger concepts. In Proceedings of the Heat Powered Cycles Conference 2009, Berlin, Germany, 7–9 September 2009. [Google Scholar]
- Wittstadt, U.; Füldner, G.; Andersen, O.; Herrmann, R.; Schmidt, F.P. A New Adsorbent Composite Material Based on Metal Fiber Technology and Its Application in Adsorption Heat Exchangers. Energies 2015, 8, 8431–8446. [Google Scholar] [CrossRef]
- Wittstadt, U.; Fueldner, G.; Laurenz, E.; Warlo, A.; Grosse, A.; Herrmann, R.; Schnabel, L.; Mittelbach, W. A novel adsorption module with fiber heat exchangers: Performance analysis based on driving temperature differences. Renew. Energy 2017, 110, 154–161. [Google Scholar] [CrossRef]
- Schwamberger, V.; Schmidt, F.P. Estimating the Heat Capacity of the Adsorbate–Adsorbent System for Adsorption Equilibria Regarding Thermodynamic Consistency. Ind. Eng. Chem. Res. 2013, 52, 16958–16965. [Google Scholar] [CrossRef]
- Dubinin, M.M.; Astakhov, V.A. Description of Adsorption Equilibria of Vapors on Zeolites over Wide Ranges of Temperature and Pressure. chapter 44; In Molecular Sieve Zeolites-II; Gould, R.F., Ed.; American Chemical Society: Washington, DC, USA, 1971; pp. 69–85. [Google Scholar] [CrossRef]
- Desai, A.; Schwamberger, V.; Herzog, T.; Jänchen, J.; Schmidt, F.P. Modeling of Adsorption Equilibria through Gaussian Process Regression of Data in Dubinin’s Representation: Application to Water/Zeolite Li-LSX. Ind. Eng. Chem. Res. 2019, 58, 17549–17554. [Google Scholar] [CrossRef]
- The International Association for the Properties of Water and Steam. Revised Release on the IAPWS Industrial Formulation 1997 for the Thermodynamic Properties of Water and Steam. 2007. Available online: http://www.iapws.org/relguide/IF97-Rev.pdf (accessed on 6 December 2019).
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Verein Deutscher Ingenieure (VDI). VDI Heat Atlas, 2nd ed.; VDI-Buch; Springer: Berlin, Germany, 2010. [Google Scholar] [CrossRef]
- Sircar, S.; Hufton, J. Why does the Linear Driving Force model for adsorption kinetics work? Adsorption 2000, 6, 137–147. [Google Scholar] [CrossRef]
- Gorbach, A.; Stegmaier, M.; Eigenberger, G. Measurement and modeling of water vapor adsorption on zeolite 4A-equilibria and kinetics. Adsorption 2004, 10, 29–46. [Google Scholar] [CrossRef]
- El-Sharkawy, I.I. On the linear driving force approximation for adsorption cooling applications. Int. J. Refrig. 2011, 34, 667–673. [Google Scholar] [CrossRef]
- Mette, B.; Kerskes, H.; Drueck, H.; Mueller-Steinhagen, H. Experimental and numerical investigations on the water vapor adsorption isotherms and kinetics of binderless zeolite 13X. Int. J. Heat Mass Transf. 2014, 71, 555–561. [Google Scholar] [CrossRef]
- Füldner, G. Stofftransport und Adsorptionskinetik in porösen Adsorbenskompositen für Wärmetransformationsanwendungen. Ph.D. Thesis, Albert Ludwig University of Freiburg, Freiburg, Germany, 2015. [Google Scholar] [CrossRef]
- Velte, A.; Füldner, G.; Laurenz, E.; Schnabel, L. Advanced Measurement and Simulation Procedure for the Identification of Heat and Mass Transfer Parameters in Dynamic Adsorption Experiments. Energies 2017, 10, 1130. [Google Scholar] [CrossRef] [Green Version]
- Chanda, R.; Selvam, T.; Avadhut, Y.S.; Kuhnt, A.; Herrmann, R.; Hartmann, M.; Schwieger, W. Key factors for the direct growth of zeolite faujasite (FAU) on metallic aluminum surface. Microporous Mesoporous Mater. 2018, 271, 252–261. [Google Scholar] [CrossRef]
- Barg, S.; Soltmann, C.; Schwab, A.; Koch, D.; Schwieger, W.; Grathwohl, G. Novel open cell aluminum foams and their use as reactive support for zeolite crystallization. J. Porous Mater. 2011, 18, 89–98. [Google Scholar] [CrossRef]
- Newton, B.J. Modeling of Solar Storage Tanks. Master’s Thesis, University of Wisconsin-Madison, Madison, WI, USA, 1995. [Google Scholar]
- VDI 4650 Part 2. Simplified Method for the Calculation of the Annual Heating Energy Ratio and the Annual Gas Utilisation Efficiency of Sorption Heat Pumps; Technical Guideline; Verein Deutscher Ingenieure (VDI): Berlin, Germany, 2013. [Google Scholar]








| Hyperparameter | Value |
|---|---|
| l | 1186.9 |
| 2.7416 × 10−4 | |
| 4.3911 × 10−6 |
| Materials | |
| Working pair | Water–zeolite Li-Y (RUB04) |
| Heat transfer fluid | Thermal oil Marlotherm LH |
| Operating conditions | |
| Driving temperature | 200 |
| Medium temperature sink | 34 |
| Low temperature source | 8 |
| Adsorber | |
| Adsorbent mass | @ 879 J kg−1−1 |
| Total volume | |
| Remaining adsorber mass | @ 882 J kg−1−1 |
| Fluid mass in adsorber | |
| Heat exchanger area | 2 |
| Overall heat transfer coefficient adsorption site–channel | 5112 W −2 −1 |
| Average heat transfer coefficient channel–fluid h | 401 W −2 −1 |
| Average overall heat transfer coefficient adsorption site–fluid | 372 W −2 −1 |
| −1 | |
| Heat transfer coefficient adsorber–chamber | 5 −1 |
| Vapor chamber volume | |
| Number of adsorber nodes | 100 |
| Evaporator and condenser | |
| Condenser mass flow rate | −1 |
| Evaporator mass flow rate | 4 −1 |
| Mass of working fluid | 20 |
| Effective heat transfer coefficient , | 4 −2 −1 |
| Storage parameters | |
| Mass of storage medium | 250 |
| Height of storage L | |
| Number of rings | 15 |
| Insulation thickness | |
| Number of layers in model | 1000 |
| Mixing model | |
| Max. amplification | 100 |
| Amplification width | |
| Heater and cooler | |
| Heater fraction | 0.9 |
| Cooler fraction | 0.25 |
| Heater extraction height | |
| Cooler extraction height | |
| Piping | |
| Mass of pipes | 5 |
| Effective length of pipes | 2 |
| Control parameters | |
| Minimal driving temperature difference at adsorber | 3 |
| Minimal temperature difference across adsorber at end of half cycle | 7 |
| kW | kW | kg/s | 1 | 1 | °C | °C | °C |
|---|---|---|---|---|---|---|---|
| 1.30 | 1.25 | 0.07 | 2.28 | 2.18 | 24.8 | 26.0 | 9.0 |
| 3.00 | 2.95 | 0.16 | 2.24 | 2.20 | 29.6 | 32.5 | 8.0 |
| 3.90 | 3.85 | 0.21 | 2.12 | 2.09 | 31.7 | 35.5 | 7.0 |
| 4.80 | 4.75 | 0.26 | 2.01 | 1.98 | 33.8 | 38.5 | 6.0 |
| 6.30 | 6.25 | 0.34 | 1.86 | 1.84 | 37.2 | 43.4 | 5.0 |
| = 2.09 | |||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schwamberger, V.; Desai, A.; Schmidt, F.P. Novel Adsorption Cycle for High-Efficiency Adsorption Heat Pumps and Chillers: Modeling and Simulation Results. Energies 2020, 13, 19. https://doi.org/10.3390/en13010019
Schwamberger V, Desai A, Schmidt FP. Novel Adsorption Cycle for High-Efficiency Adsorption Heat Pumps and Chillers: Modeling and Simulation Results. Energies. 2020; 13(1):19. https://doi.org/10.3390/en13010019
Chicago/Turabian StyleSchwamberger, Valentin, Aditya Desai, and Ferdinand P. Schmidt. 2020. "Novel Adsorption Cycle for High-Efficiency Adsorption Heat Pumps and Chillers: Modeling and Simulation Results" Energies 13, no. 1: 19. https://doi.org/10.3390/en13010019
APA StyleSchwamberger, V., Desai, A., & Schmidt, F. P. (2020). Novel Adsorption Cycle for High-Efficiency Adsorption Heat Pumps and Chillers: Modeling and Simulation Results. Energies, 13(1), 19. https://doi.org/10.3390/en13010019