Battery Electric Vehicle Eco-Cooperative Adaptive Cruise Control in the Vicinity of Signalized Intersections

Abstract

This study develops a connected eco-driving controller for battery electric vehicles (BEVs), the BEV Eco-Cooperative Adaptive Cruise Control at Intersections (Eco-CACC-I). The developed controller can assist BEVs while traversing signalized intersections with minimal energy consumption. The calculation of the optimal vehicle trajectory is formulated as an optimization problem under the constraints of (1) vehicle acceleration/deceleration behavior, defined by a vehicle dynamics model; (2) vehicle energy consumption behavior, defined by a BEV energy consumption model; and (3) the relationship between vehicle speed, location, and signal timing, defined by vehicle characteristics and signal phase and timing (SPaT) data shared under a connected vehicle environment. The optimal speed trajectory is computed in real-time by the proposed BEV eco-CACC-I controller, so that a BEV can follow the optimal speed while negotiating a signalized intersection. The proposed BEV controller was tested in a case study to investigate its performance under various speed limits, roadway grades, and signal timings. In addition, a comparison of the optimal speed trajectories for BEVs and internal combustion engine vehicles (ICEVs) was conducted to investigate the impact of vehicle engine types on eco-driving solutions. Lastly, the proposed controller was implemented in microscopic traffic simulation software to test its networkwide performance. The test results from an arterial corridor with three signalized intersections demonstrate that the proposed controller can effectively reduce stop-and-go traffic in the vicinity of signalized intersections and that the BEV Eco-CACC-I controller produces average savings of 9.3% in energy consumption and 3.9% in vehicle delays.

1. Introduction

The United States is one of the world’s prime petroleum consumers, burning more than 20% of the planet’s total refined petroleum, and the surface transportation sector alone accounts for around 69% of the United States’ total petroleum usage [1]. This presents the transportation sector with three important challenges: availability of fuel to drive vehicles, emissions of greenhouse gases, and vehicular crashes. It is, therefore, important to reduce petroleum consumption to make surface transportation safer, more efficient, and more sustainable [2].

The advent of communication and information technology has enabled vehicle-to-vehicle and vehicle-to-infrastructure connectivity, so that various data, such as signal phase and timing (SPaT), vehicle trajectory, and velocity, can be transmitted and utilized. The advanced communication abilities of connected vehicles ensures that information is updated at a very high rate, which enables researchers to develop connected transportation systems meeting safety, economy, and efficiency challenges [3]. Studies have shown that vehicles have high fuel consumption rates when approaching signalized intersections because of vehicle acceleration/deceleration maneuvers during stop-and-go traffic [2,4]. Over the past few decades, researchers have worked on optimizing traffic signal planning to reduce traffic delay and fuel consumption [5,6]. In recent years, a number of studies have focused on developing eco-driving algorithms to help vehicles approach signalized intersections using connected vehicle technologies. These eco-driving strategies aim to provide, in real-time, recommendations to individual drivers or vehicles so that vehicle maneuvers can be appropriately adjusted to reduce fuel consumption and emission levels [7,8,9].

Most of the studies in this area have been focused on developing eco-driving strategies for internal combustion engine vehicles (ICEVs). For example, Malakorn and Park proposed to reduce vehicle fuel consumption by minimizing vehicle acceleration maneuvers using a cooperative adaptive cruise control system under a connected environment [10]. Another study [2] developed an optimal control strategy by using dynamic programming and recursive pathfinding techniques, and the control logic was validated by an agent-based modeling approach. In addition, a schedule optimization method was proposed in [11] to search for “green-windows” so that vehicles can traverse multiple signalized intersections by minimizing full stops. A further-improved approach was developed by Guan and Frey to generate a brake-specific fuel map so that the optimized gear ratio can be computed to save fuel levels [12].

In addition to the studies that focused on ICEVs, a few studies have investigated eco-driving strategies for battery electric vehicles (BEVs) near signalized intersections. Using SPaT information passed from connected infrastructure, an energy-optimized speed trajectory can be computed for BEVs while traveling on signalized arterials, thus extending the BEV’s range. An eco-driving technique for BEVs was developed in [13]. In that work, the vehicle trajectory control problem was formulated as an optimization problem to minimize the summation of vehicle power, and Bellman’s dynamic programming algorithm was used to compute the optimal solution. However, a simple energy model was used in this study by assuming that the recharge efficiency is a constant value. Another BEV eco-driving algorithm was proposed in [14]. A VT-Micro model-based energy consumption model was developed for different BEV operation modes (including acceleration, deceleration, idling, and cruising). Subsequently, an eco-driving model, which used the developed energy model, was proposed for a single signalized intersection. Several example trips in the case study illustrate the proposed eco-driving method’s ability to reduce energy consumption efficiently. However, the proposed energy consumption model was a statistical model based on limited collected data, thus the accuracy may not be sufficient for developing an optimal control strategy for dynamic vehicle maneuvers. Moreover, the vehicle dynamics model was not considered in the constraints to compute the acceleration level, so the calculation of the optimal solution may use an unrealistic acceleration level.

The same energy consumption model was used in [15] to develop a connected BEV eco-driving system. A model predictive control logic was considered in the control system to force the vehicle to follow the optimal speed trajectory as closely as possible. A field test with four participants demonstrated an average of 22% energy savings for automated driving with the proposed eco-driving system. However, a 2012 Ford Escape with a hybrid engine was used for the field test in this study, and this vehicle was assumed to be representative of an actual BEV’s performance.

An analytical model to calculate a BEV’s optimum vehicle trajectory was proposed in [16], with the goal of minimizing electricity usage with consideration of intersection queues. Furthermore, an approximation model was proposed to increase computation efficiency for real-time applications. A 47.5% energy savings was found when evaluating field data from a six-intersection corridor. However, the objective function was the summation of energy consumption from the tractive force only, and the braking force was assumed to be 100% transferable to battery power. In addition, the work in [17] provided a solution to minimize BEVs’ energy consumption while traversing a sequence of signalized intersections and always getting a green indication. A simple simulation network (AIMSUN) with five intersections was used in the case study. A sensitivity analysis with different market penetration rates was tested to show a 10% energy savings for a 40% penetration rate. However, the computation of energy consumption in this study did not consider regenerative braking.

There are several issues with the aforementioned studies of BEV eco-driving strategies: a lack of realistic energy consumption models to accurately compute the instantaneous energy consumption when BEVs travel through signalized intersections, and the lack of a vehicle dynamics model to constrain vehicle acceleration maneuvers. In addition, although many previous studies developed eco-driving strategies for ICEVs and BEVs, there is no comparison to demonstrate the differences in the energy-optimal solutions for each. To address these issues, this study develops a connected eco-driving controller for BEVs, called the BEV Eco-Cooperative Adaptive Cruise Control at Intersections (Eco-CACC-I). The developed controller can assist BEVs negotiating signalized intersections by minimizing their energy consumption. The calculation of optimal vehicle trajectory is formulated as an optimization problem subject to the following constraints: (1) vehicle acceleration/deceleration behavior, defined by a vehicle dynamics model; (2) vehicle energy consumption behavior, defined by a BEV energy consumption model; and (3) the relationship between vehicle speed, location, and signal timing, defined by vehicle characteristics and SPaT data shared under a connected vehicle environment. The optimal speed trajectory is computed in real-time by the proposed BEV Eco-CACC-I controller so that a BEV can follow the optimal speed while negotiating a signalized intersection. The proposed BEV controller was tested in a case study to investigate its performance under various speed limits, roadway grades, and signal timings. In addition, a comparison of the optimal speed trajectories for BEVs and ICEVs was conducted to investigate the impact of vehicle engine types on eco-driving solutions. Lastly, the proposed controller was implemented in microscopic traffic simulation software to test its networkwide performance. The test results from an arterial corridor with three signalized intersections demonstrate that the proposed controller can effectively reduce stop-and-go traffic in the vicinity of signalized intersections, and that the BEV Eco-CACC-I controller produces average savings of 9.3% in energy consumption and 3.9% in vehicle delays.

The remainder of this paper is presented as follows. The proposed BEV Eco-CACC-I system and the vehicle dynamics and energy consumption models are described in the next section. Afterward, the details of the proposed system testing on the case study section to investigate the impacts of various factors on system performance are presented. This is followed by implementing the proposed controller into microscopic traffic simulation software to quantify the networkwide impacts. The last section provides conclusions and recommendations for future research.

2. Model Development

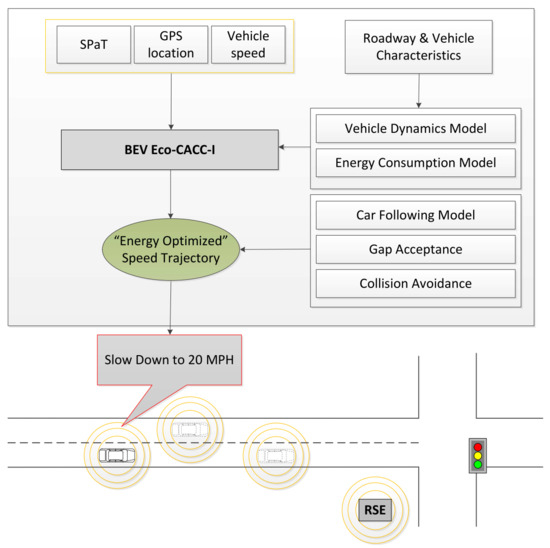
2.1. Eco-CACC-I for BEVs

In previous studies, an eco-driving system for gasoline-powered vehicles, named ICEV Eco-CACC-I, was developed and tested under a simulated environment and real-world field tests [18,19,20,21]. The ICEV Eco-CACC-I system computes real-time, fuel-optimized speed profiles that vehicles can follow so that they can proceed through signalized intersections while consuming minimum amounts of fuel. In the previous field test study, we implemented the developed eco-driving system into a real-world automated vehicle as an adaptive cruise control system [19]. Note that the developed Eco-CACC-I system does not directly optimize the collaboration between multiple vehicles. Here, the term “cooperative” means the vehicles equipped with the developed system can cooperate with signalized intersections under a connected-vehicle environment. During the previous network-level simulation test, the recommended speed computed by the developed system was used as a variable speed limit, which worked together with other constraints, such as the car following model and collision avoidance constraint, to control vehicle speed [21]. The same control logic of the previously developed algorithm was used in this study to develop an Eco-CACC-I controller that allows BEVs to drive smoothly through signalized intersections with minimal energy consumption and thus extend their range.

The same control environment setup for ICEV Eco-CACC-I was used here to develop the BEV Eco-CACC-I. The interested reader may read about the previous work in [19,21]. The control region was defined as a distance upstream of the signalized intersection (d_up) to a distance downstream of the intersection (d_down) in which the BEV Eco-CACC-I controller optimizes the speed profiles of vehicles approaching and leaving signalized intersections. Upon approaching a signalized intersection, the vehicle may accelerate, decelerate, or cruise (maintain a constant speed) based on a number of factors, such as vehicle speed, signal timing, phase, distance to the intersection, road grade, and headway distance, etc. [2]. We assumed no leading vehicle ahead of the BEV so that we could compute the energy-optimized vehicle trajectory for the BEV without considering the impacts of other surrounding vehicles. The computed optimal speed was used as a variable speed limit, denoted by v_e(t), which is one of the constraints on the BEV longitudinal motion. When a BEV travels on the roadway, there are other constraints to be considered, including the allowed speed constrained by the vehicle dynamics model, steady-state car following mode, collision avoidance constraint, and roadway speed limit. All of these constraints work together to control the vehicle speed. In this way, the proposed system can also be used in the situation that the BEV follows a leading vehicle and the vehicle speed can be computed by v(t) = min(v₁(t), v₂(t), v₃(t), v₄(t), v_e(t)) using the following constraints:

(1)

The maximum speed v₁(t) allowed by the vehicle acceleration model for a given vehicle throttle position;

(2)

The maximum speed v₂(t) constrained by the steady-state vehicle spacing in the simulation software;

(3)

The speed limit of v₃(t) to avoid a rear-end vehicle collision; and

(4)

The maximum speed v₄(t) allowed on the road.

Within the control region, the vehicle’s behavior can be categorized into one of two cases: (1) the vehicle can pass through the signalized intersection without decelerating or (2) the vehicle must decelerate to pass through the intersection. Given that vehicles drive in different manners for cases 1 and 2, the BEV Eco-CACC-I strategies were developed separately for the two cases.

Case 1 does not require the vehicle to decelerate to traverse the signalized intersection. In this case, the cruise speed for the vehicle to approach the intersection during the red indication can be calculated by Equation (1) to maximize the average vehicle speed during the control region.

$$u_c=min\left(\frac{d_{up}}{t_r},u_f\right)$$

(1)

When the vehicle enters the control region, it should adjust speed to u_c according to the vehicle dynamics model illustrated later in Equations (5) through (7). After the traffic light turns from red to green, the vehicle accelerates from the speed u_c to the maximum allowed speed (speed limit u_f) by following the vehicle dynamics model until it leaves the control region.

In case 2, the vehicle’s energy-optimized speed profile is illustrated in Figure 1. After entering the control region, the vehicle with the initial speed of u(t₀) needs to brake at a deceleration level denoted by a, then cruise at a constant speed of u_c to approach the signalized intersection. After passing the stop bar, the vehicle should increase speed to u_f per the vehicle dynamics model, and then cruise at u_f until the vehicle leaves the control region. In this case, the only unknown variables are the upstream deceleration rate a and the downstream throttle f_p. The following optimization problem was formulated to compute the optimum vehicle speed profile associated with the least energy consumption.

Assuming a BEV enters the Eco-CACC-I control region at time t₀ and leaves the control region at time t₀ + T, the objective function entails minimizing the total energy consumption level as:

$$min{{\displaystyle \int }}_{t_0}^{t_0+T}EC\left(u\left(t\right)\right)·dt$$

(2)

where EC denotes the electric energy consumption at instant t using Equations (8) through (11). The constraints to solve the optimization problem can be built according to the relationships between vehicle speed, location, and acceleration/deceleration, as presented below:

$$u\left(t\right):\{\begin{array}{cc}\begin{array}{c}u\left(t\right)=u\left(t_0\right)-at\\ u\left(t\right)=u_c\end{array} & \begin{array}{c}{t}_0\le t\le t_1\\ t_1<t\le t_r\end{array}\\ \begin{array}{c}u\left(t+∆t\right)=u\left(t\right)+\frac{F\left(f_p\right)-R\left(u\left(t\right)\right)}{m}∆t\\ u\left(t\right)=u_f\end{array}& \begin{array}{c}{t}_r<t\le t_2\\ t_2<t\le t_0+T\end{array}\end{array}$$

(3)

$$\begin{array}{c}u\left(t_0\right)·t-\frac{1}{2}a{t}^2+u_c\left(t_r-t_1\right)=d_{up}\\ u_c=u\left(t_0\right)-a\left(t_1-t_0\right)\\ \begin{array}{c}{{\displaystyle \int }}_{t_r}^{t_2}u\left(t\right)dt+u_f\left(t_0+T-t_2\right)=d_{down}\\ u\left(t_2\right)=u_f\\ \begin{array}{c}{a}_{min}<a\le a_{max}\\ f_{min}\le f_p\le f_{max}\\ u_c>0\end{array}\end{array}\end{array}$$

(4)

In Equation (3), function F denotes the vehicle tractive force calculated by Equation (6), and function R represents all the resistance forces (aerodynamic, rolling, and grade resistance forces) calculated by Equation (7). Note that the maximum deceleration was limited by the comfortable threshold felt by average drivers [2]. The throttle value ranges between 0 and 1. To solve the optimization problem, dynamic programming was used to list all the candidate solutions with the associated electric energy consumption levels. This allowed calculation of optimal parameters for upstream deceleration a and downstream throttle f_p by finding the candidate solution associated with the minimum energy consumption for vehicles passing the control region. To solve the proposed optimization problem in real-time, an A-star search method was selected to ensure fast and efficient computations. The A-star search method is one of the best and most popular path search methods to find the lowest cost path using a heuristic function [22]. The deceleration and throttle levels are considered as constant values in the A-star algorithm when computing the future cost. However, given that the optimal solution is recomputed every decisecond, the acceleration/deceleration level can also be updated every decisecond, thus producing a varying acceleration/deceleration maneuver. In the proposed optimization problem, first, a constant throttle level was assumed (e.g., 0.6) to find the optimal deceleration level, which corresponds to the minimal energy consumption for the entire trip from d_down to d_up. In this way, the starting speed (cruise speed u_c) and the ending speed (speed limit u_f) on the downstream roadway are known, so the optimal throttle level which corresponds to the minimal energy consumption for the downstream trip can be located. The details of how the A-star algorithm outperforms other pathfinding algorithms and the steps to implement the A-star algorithm can be found in [22].

2.2. Vehicle Dynamics Model

The proposed BEV Eco-CACC-I system uses a vehicle dynamics model to compute vehicle acceleration behavior. Here, vehicle acceleration is based on the vehicle dynamics model formulated in [23,24], where acceleration level is related to throttle level and vehicle velocity. The vehicle dynamics model is summarized as

$$u\left(t+∆t\right)=u\left(t\right)+\frac{F\left(t\right)-R\left(t\right)}{m}∆t$$

(5)

$$F=\min \left(3600f_p\beta {\eta }_D\frac{P_{max}}{u},m_{ta}g\mu \right)$$

(6)

$$R\left(t\right)=\frac{\rho }{25.92}{\mathrm{C}}_d{\mathrm{C}}_h{\mathrm{A}}_{f}u{\left(t\right)}^2+mg\frac{c_{r0}}{1000}\left(c_{r1}u\left(t\right)+c_{r2}\right)+mg{R}_g$$

(7)

where F and R are the tractive and resistance forces on the vehicle (N); η_D (unitless) denotes the drivetrain losses; β (unitless) represents the gear reduction factor (light-duty vehicle uses the value of 1.0); f_p (unitless) denotes the throttle input from the driver; m_ta (kg) represents the vehicle mass on the tractive axle; P_max is the maximum engine power (kW); μ (unitless) denotes the adhesion coefficient between the vehicle tire and road surface; ρ is the sea-level air density (kg/m³) at 15 °C temperature; A_f denotes the frontal area of the vehicle (m²); C_d (unitless) represents the drag coefficient; C_h (unitless) is the correction factor for altitude; c_r0, c_r1, and c_r2 are rolling resistance constant values (unitless); m (kg) represents the mass of the vehicle; and G (unitless) denotes the road grade.

2.3. Energy Consumption Model for BEVs

The Virginia Tech comprehensive power-based electric vehicle energy consumption model (VT-CPEM), developed in [25], was used in the proposed Eco-CACC-I system to compute instantaneous energy consumption levels for BEVs. The model was selected here for three main reasons: (1) speed is the only required input variable for this model, so it is easy to use to solve the proposed optimization problem; (2) the model has been validated and has demonstrated its ability to produce good accuracy compared to empirical data; and (3) the model can be calibrated to a specific vehicle using publicly available data. The VT-CPEM is a quasi-steady backward highly resolved power-based model, which only requires the instantaneous speed and the electric vehicle characteristics as input to compute the instantaneous power consumed. The VT-CPEM model is summarized in the following equations.

$$EC\left(t\right)={{\displaystyle \int }}_0^t{P}_B\left(t\right)·dt$$

(8)

$$P_B\left(t\right)=\{\begin{array}{cc}\frac{P_W\left(t\right)}{{\eta }_D·{\eta }_{EM}·{\eta }_B}+P_A& \forall P_{Wheels}\left(t\right)\ge 0\\ P_W\left(t\right)·{\eta }_D·{\eta }_{EM}·{\eta }_B·{\eta }_{rb}\left(t\right)+P_A& \forall P_{Wheels}\left(t\right)<0\end{array}$$

(9)

$$P_W\left(t\right)=\left(ma\left(t\right)+R\left(t\right)\right)·u\left(t\right)$$

(10)

$${\eta }_{rb}\left(t\right)={\left[e^{\left(\frac{\lambda }{\left|a\left(t\right)\right|}\right)}\right]}^{-1}$$

(11)

where EC (kWh) represents the energy consumption from time 0 to t; P_W denotes the power at the wheels (kW); P_B is the power consumed by (regenerated to) the electric motor (kW); P_A is the power consumed by the auxiliary systems (kW); η_D and η_EM (unitless) are the driveline efficiency and the efficiency of the electric motor, respectively; η_B (unitless) denotes the efficiency from a battery to an electric motor; η_rb represents the regenerative braking energy efficiency (unitless), which can be computed using Equation (11); the parameter λ (unitless) has been calibrated (λ = 0.0411) in [25] using empirical data described in [26]; and R(t) represents the resistance force (N) computed in Equation (7).

3. Case Study

The case study simulated the proposed BEV Eco-CACC-I algorithm to investigate the impact of signal timing, speed limit, and road grade on the optimal solution.

In addition, two electric vehicles (a 2015 Nissan Leaf and a 2015 Tesla Model S) were considered in the simulation test to see if a particular vehicle model with different weight and engine powers affected the optimal solution. To compare BEV and ICEV optimal solutions, two ICEVs (a 2015 Honda Fit and a 2015 Cadillac SRX) were used for the same simulation test.

3.1. Test Eco-CACC-I for BEVs

The simulated test road consisted of a single signalized intersection with a control length starting 200 m upstream and ending 200 m downstream of the intersection (total length of 400 m). An automated connected vehicle, a 2015 Nissan Leaf equipped with the Eco-CACC-I system, was assumed to follow the optimal speed profile calculated by the Eco-CACC-I algorithm in that 400-m distance. Combinations of different speed limits (25, 30, 40, and 50 mph), signal indication offsets (15, 20, 25, and 30 s) and road grades (+3% and −3%) were tested. Given that the test results for the Nissan Leaf under various speed limits were very similar, the test results for the 25-mph speed limit alone are presented in Figure 2 and Figure 3.

Figure 2 demonstrates the test results under a 25-mph speed limit for different signal timings and road grade values. Note that the vehicle with an initial speed of 25 mph did not need to slow down for the 15-s red indication, so the plots for this case were not included. Each image in Figure 2 presents the sampling of numerous feasible solutions (speed profiles) for each combination of parameters. For instance, the right bottom image in Figure 2 includes 29 curves. Each curve represents a feasible solution when a vehicle approaches a signalized intersection with a certain deceleration level (a_i). The downstream throttle level was the optimal throttle corresponding to the minimal energy consumption given the upstream deceleration level of a_i. Each feasible solution is plotted in a different color, and the optimal solution, which corresponds to the minimal energy consumption trajectory, is presented in a bold red color. It should be noted that all the images in the left column in Figure 2 show that the speed profile associated with the maximum deceleration level was the optimal solution for the uphill direction. Furthermore, all the images in the right column in Figure 2 show that the speed profile associated with the minimum deceleration level was the optimal solution for the downhill direction.

The corresponding energy consumption levels for each feasible solution (speed profile) are presented in Figure 3. Note that the solution index in the x-axis represents the 1st solution, 2nd solution … nth solution, ordered in ascending order by deceleration levels. All the images in the left column in Figure 3 show that the upstream trip regenerated minimum electric power; much less battery power was regenerated than was consumed. In this case, the cruise speed was the most important factor in identifying the optimal solution, as higher cruise speeds associated with higher deceleration levels result in less energy consumption for the entire trip. Consequently, the maximum deceleration level corresponds to the optimal solution for a BEV driving in the uphill direction. All the images in the right column in Figure 3 illustrate that the upstream trip generated equal or slightly higher electric power than the battery power consumed during the downstream trip due to the impact of gravity in the downhill direction. In this case, the deceleration level was the most important factor in identifying the optimal solution. Lower deceleration levels correspond to longer deceleration times and more regenerative electric power upstream of the intersection, which can result in lower energy consumption for the entire trip. Therefore, the minimal deceleration level corresponds to the optimal solution for a BEV driving in the downhill direction.

The Nissan Leaf is a compact BEV with an 80-HP engine; to investigate the impact of engine size on the optimal control strategy, a 2015 Tesla Model S with a much more powerful 283 HP engine was also tested. The same simulation was conducted assuming a connected and automated Tesla Model S equipped with the Eco-CACC-I controller. The simulation results were very similar to the Nissan Leaf results. There were two main differences. First, downstream of the intersection, the Tesla could accelerate to the maximum allowed speed (speed limit) much more quickly in the downhill direction given that the vehicle is more powerful than the Nissan Leaf. Second, the energy consumption for the Tesla Model S was higher since it weighs more. However, the energy consumption curves across the solutions from minimum to maximum deceleration levels showed the same trends, so the same optimal solution could be found for both vehicles. Given that the test results for the Nissan Leaf are already illustrated, the plots for the Tesla are not presented here. According to the test results for the two BEVs, the optimal solutions for the downhill and uphill directions can be summarized as follows:

• Downhill direction: The optimal speed profile corresponds to the minimum deceleration level in the solution space.

  ○

  Upstream—lower cruise speed produces longer brake time and more regenerative energy.

  ○

  Downstream—lower cruise speed means more energy consumption downstream; however, the benefit of energy regeneration upstream exceeds the additional needs for energy downstream.

• Uphill direction: The optimal speed profile corresponds to the maximum deceleration level in the solution space.

  ○

  Upstream—different from the solution for the downhill direction, the vehicle regenerates minimum energy by decelerating in the uphill direction.

  ○

  Downstream—the vehicle needs the maximum cruise speed while proceeding through the intersection so that the downstream trip requires less energy.

3.2. Eco-CACC-I for ICEVs

The Eco-CACC-I for ICEVs previously developed in [19,20] was considered in comparison with the Eco-CACC-I for BEVs. In this model, the optimization problem was formulated using Equations (2) through (4), and the same vehicle dynamic model used in Equations (5) through (7). Note that the Virginia Tech comprehensive power-based fuel consumption model (VT-CPFM-1) was used in place of the BEV energy model in Equations (8) through (11). More details of the Eco-CACC-I controller for ICEVs can be found in [19,20].

The same simulation was conducted for a 2015 Honda Fit, which has an engine power and weight similar to the 2015 Nissan Leaf. The test results are presented in Figure 4 and Figure 5. Figure 4 shows the test results for a speed limit of 25 mph for different signal timings and roadway grades. All the images in the left column in Figure 4 demonstrate that the speed profile with a deceleration level in the middle area (between the minimum and maximum values) was the optimal solution for the uphill direction. All the images in the right column in Figure 4 demonstrate that the speed profile associated with the maximum deceleration level was the optimal solution for the downhill direction. The corresponding energy consumption levels for each feasible solution (speed profile) in the solution space are presented in Figure 5. Note that the solution index along the x-axis is also ranked and ordered in a descending manner based on the deceleration level. The energy consumption unit is “liters” for ICEVs. In addition, unlike BEVs that regenerate energy while braking, ICEVs always consume fuel during the trip. All the images in the left column in Figure 5 show that the vehicle consumed more energy to reach a higher cruise speed in the uphill direction upstream of the intersection. However, higher cruise speeds resulted in less energy consumption downstream of the intersection. Therefore, the optimal solution for ICEVs driving in the uphill direction is somewhere in the mid-range, depending on the vehicle’s specifications and roadway grade. All the images in the right column in Figure 5 demonstrated that different deceleration levels did not change the ICEV’s energy consumption while traveling downhill. Therefore, higher cruise speeds resulted in the same level of fuel consumption upstream of the intersection. However, higher cruise speeds resulted in less energy consumption downstream of the intersection. In this case, the deceleration level is the most important factor in locating the optimal solution. Higher deceleration levels corresponded to lower energy consumption for the downstream portion, while energy consumption remained the same for the upstream portion. Therefore, the maximum deceleration level corresponds to the optimal solution for ICEVs driving in the downhill direction.

The Honda Fit is a compact gasoline vehicle with a 97-HP engine. To examine whether ICEV optimal solutions are general or engine specific, a 2015 Cadillac SRX with a much more powerful engine of 230 HP was also tested. The same tests were conducted, assuming a connected automated Cadillac SRX equipped with the Eco-CACC-I controller. The simulation results for the two ICEVs were very similar. There were two differences. First, downstream of the intersection, the Cadillac could accelerate to the maximum allowed speed (speed limit) faster in the downhill direction, given that it had more engine power compared to the Honda Fit. Second, the energy consumption for the Cadillac was almost double that of the Honda Fit due to its larger size. However, the energy consumption curves across the solutions from minimum to maximum deceleration levels showed similar trends, demonstrating that the ICEV optimum strategies appear to be general. According to the test results for the two ICEVs, the optimal solutions produced by the Eco-CACC-I system for the downhill and uphill directions can be summarized as follows:

• Downhill direction: The optimal speed profile corresponds to the maximum deceleration level in the solution space.

  ○

  Upstream—different deceleration levels do not change the ICEV’s energy consumption during braking, so higher cruise speeds consume a similar amount of fuel.

  ○

  Downstream—higher cruise speeds at the stop bar result in less energy consumption downstream.

• Uphill direction: The optimal speed profile corresponds to the maximum deceleration level in the solution space.

  ○

  Upstream—unlike the downhill direction, the vehicle consumes more energy to reach a higher cruise speed while traveling uphill.

  ○

  Downstream—higher cruise speeds result in less energy consumption downstream. Therefore, the optimal solution sits in the mid-range, depending on the vehicle’s weight, engine power, and roadway slope.

3.3. Test Results Analysis and Comparison

The test results indicate that the optimal solutions for BEVs and ICEVs are quite different. The optimal solutions for BEVs and ICEVs when decelerating upstream of an intersection are summarized in

Table 1. Optimal solutions for BEVs and ICEVs Eco-CACC-I systems when the vehicle needs to decelerate to traverse a signalized intersection.

Roadway Grade	BEV	ICEV
Uphill	Maximum deceleration	Mid-range deceleration
Downhill	Minimum deceleration	Maximum deceleration

. For downhill roadways, BEVs require longer deceleration times to accumulate more regenerative power to minimize overall energy consumption when traversing the intersection. Conversely, ICEVs need the maximum deceleration level (minimum deceleration time) to minimize overall energy consumption. For uphill approaches, BEVs need to minimize deceleration time to reach the approach stop line at maximum speed, saving energy downstream while accelerating back to the roadway speed limit. Contrarily, the optimum ICEV deceleration level is typically in the mid-range to minimize overall energy consumption. The comparison demonstrates that the energy-optimum solution for BEVs is different from that for ICEVs, as they consume energy differently. The findings in the case study also prove that previous studies, which only considered the optimization of vehicle acceleration and deceleration movements and ignored the specific vehicle energy model, may not correctly compute the energy-optimal eco-driving solutions for different types of vehicles.

3.4. Test Eco-CACC-I Controllers in Microscopic Traffic Simulation Software

The Eco-CACC-I controllers for BEVs and ICEVs were implemented in the microscopic traffic simulation software INTEGRATION to evaluate their performance. The INTEGRATION software is a trip-based microscopic traffic assignment, simulation, and optimization model that has the capability of modeling networks of up to 3,000,000 vehicle departures. A more-detailed description of INTEGRATION is provided in the literature [27,28].

A simulated traffic network, composed of three signalized intersections, as shown in Figure 6, was used in this test. The major road has a free-flow speed of 40 mph, a speed at a capacity of 30 mph, a saturation flow rate of 1600 veh/h/lane, and a jam density of 160 veh/km/lane. The total length of the main direction roadway is 4000 m. The three traffic signals (1000 m apart) have the same signal timing plan with a 60-s cycle length and 42-s phase length for the main street with 5-s intergreen time (yellow and all-red time indication). The signal offsets are 0 s for all traffic signals. The traffic volume in the main direction is set to be 400 veh/h/lane.

Given that the energy optimum solutions for ICEVs and BEVs are very different for the downhill direction, here we set a −3% grade for the main direction road. We modeled a 2015 Nissan Leaf and a 2015 Honda Fit to represent BEVs and ICEVs in the simulation. Four scenarios, described below, were used to compare the vehicle trajectories.

• Scenario 1 (uninformed drive for ICEVs): All the vehicles were ICEVs, and no Eco-CACC controller was activated. Each vehicle only followed the normal traffic rules (such as vehicle dynamics model, car-following model, collision avoidance) while traversing the network.
• Scenario 2 (uninformed drive for BEVs): All the vehicles were BEVs, and no Eco-CACC controller was activated. Each vehicle only followed the normal traffic rules (such as vehicle dynamics model, car-following model, collision avoidance) while traversing the network.
• Scenario 3 (informed drive by ICEV Eco-CACC-I): All the vehicles were ICEVs, and the ICEV Eco-CACC-I controller was activated when a vehicle was within a 200-m range (both upstream and downstream) of the signalized intersection.
• Scenario 4 (informed drive by BEV Eco-CACC-I): All the vehicles were BEVs, and the BEV Eco-CACC-I controller was activated when a vehicle was within a 200-m range (both upstream and downstream) of the signalized intersection.

The vehicle trajectories near the first signalized intersection in the four scenarios are presented in Figure 7. Figure 7a presents the speed trajectories of the uninformed drive for ICEVs. We can clearly see that a total of nine vehicles came to a full stop upstream of the first intersection (as demonstrated by the horizontal trajectory lines). Figure 7b presents the speed trajectories of an uninformed drive for BEVs, which were very similar to the trajectories in (a) with nine fully stopped vehicles before the intersection. Figure 7c presents the speed trajectories optimized by ICEV Eco-CACC-I. The findings in Section 3.2 and Table 1 show that an ICEV equipped with an Eco-CACC-I controller quickly reduced speed and then cruised at a constant speed to approach the intersection during red signal indication when traveling in the downhill direction. The INTEGRATION simulation results in scenario 3 were demonstrated to be consistent with our previous findings, and the vehicles produced very smooth trajectories without having to come to a full stop, as shown in Figure 7c. In addition, the findings in Section 3.1 and Table 1 showed that the proposed BEV Eco-CACC-I controller would suggest that the vehicle decelerate mildly to maximize the deceleration time when traversing a signalized intersection on a downhill roadway, which was consistent with the simulation results in scenario 4, as shown in Figure 7d. The test results in the four scenarios proved that the microscopic traffic simulation with the ICEV and BEV Eco-CACC-I controller enabled in the INTEGRATION software produced consistent results to our findings in Table 1. In addition, the comparison of the simulation results in scenarios 2 and 4 showed that the BEV Eco-CACC-I controller produced average savings of 9.3% in energy consumption and 3.9% in vehicle delay.

4. Conclusions and Future Work

A review of the literature shows that there are several issues in the BEV eco-driving strategies developed from existing studies, including a lack of realistic energy consumption models to accurately compute the instantaneous energy consumption when BEVs travel through signalized intersections, and the lack of a vehicle dynamics model to constrain vehicle acceleration maneuvers. In addition, although several previous studies developed eco-driving strategies for ICEVs and BEVs, there is no direct comparison to demonstrate the differences in the energy-optimal solutions for each. To address these issues, this study developed a BEV Eco-CACC-I controller. The developed controller can assist BEVs while traversing signalized intersections with minimal energy consumption. The calculation of the optimal vehicle trajectory was formulated as an optimization problem under the constraints of (1) vehicle acceleration/deceleration behavior, defined by a vehicle dynamics model; (2) vehicle energy consumption behavior, defined by a BEV energy consumption model; and (3) the relationship between vehicle speed, location and signal timing, defined by vehicle characteristics and SPaT data shared under the connected vehicle environment. The optimal speed trajectory was computed in real-time by the proposed BEV Eco-CACC-I controller so that a BEV could follow the optimal speed while negotiating a signalized intersection. The proposed BEV controller was tested in a case study to investigate the performances under various speed limits, roadway grades, and signal timings. In addition, a comparison of the optimal speed trajectories for BEVs and ICEVs was conducted to investigate the impact of vehicle engine types on eco-driving solutions. The comparison results illustrate that previous studies, which only considered the optimization of acceleration/deceleration and ignored the specific vehicle energy model, may not correctly compute the energy-optimal eco-driving solution for different vehicle types. Lastly, the proposed controller was implemented in microscopic traffic simulation software to test its networkwide performance. The test results from an arterial corridor with three signalized intersections demonstrated that the proposed controller can effectively reduce stop-and-go traffic in the vicinity of signalized intersections, and that the BEV Eco-CACC-I controller produced average savings of 9.3% in energy consumption and 3.9% in vehicle delays.

Although the proposed controller was demonstrated to produce very positive energy and delay savings for BEVs from the simulation tests, currently the developed Eco-CACC-I controller can only optimize BEVs or ICEVs separately. In future work, an integrated optimization for different types of vehicles will be considered in developing optimum solutions for mixed traffic conditions. In addition, more simulation tests with various traffic volumes, market penetration rates, signal timings, etc., will be considered to test the proposed controller further.