Exploring the Potentials of Artificial Neural Network Trained with Differential Evolution for Estimating Global Solar Radiation
Abstract
:1. Introduction
2. Literature Review
3. Material and Methods
3.1. Artificial Neural Networks
3.2. Differential Evolution
| Algorithm 1: Classical Differential Evolution Algorithm |
 |
3.3. Site Description and Data Collection
3.4. Relation between Extraterrestrial and the Other Factors
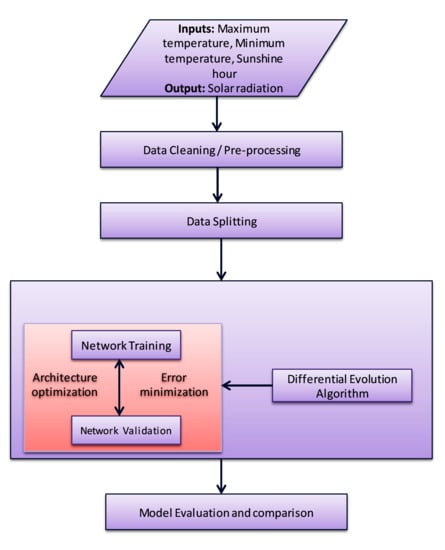
3.5. Model Development
3.5.1. Network Typology and Setup
3.5.2. Data Splitting
3.5.3. Model Implementation and Optimization
3.5.4. Model Performance Evaluation
- Root-mean-square error:
- Coefficient of determination:
- Nash-Sutcliffe efficiency index:where the observed and predicted values are given as and respectively and their mean values are given as and respectively and X is the data size.
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Symbol/Acronym | Description |
| Air Pressure | |
| MSE | Mean square error |
| Altitude | |
| Mean/average Temperature | |
| Average daily cloudiness | |
| Minimum Temperature | |
| Average Pressure | |
| Maximum Temperature | |
| Clearness index | |
| EF | Model Efficiency |
| , | Clearness index and global clearness index respectively |
| M | Month |
| Coefficient of determination | |
| NS | Nash–Sutcliffe coefficient |
| R | Correlation coefficient |
| nRMSE | Normalized root mean square error |
| D | Day |
| nMBE | Normalized mean bias error |
| Extraterrestrial radiation on a horizontal surface | |
| P | Pressure |
| GPI | Global performance index |
| Rainfall/precipitation | |
| Global solar radiation | |
| RE | Relative error |
| , | Latitude, Longitude |
| Relative humidity | |
| Maximum sunshine hour | |
| RRMSE | Relative root mean square error |
| MAE | Mean absolute error |
| RMSE | Root mean square error |
| MPBE | Mean Absolute Percentage Error |
| Sunshine hour | |
| MABE | Mean absolute bias error |
| T | Temperature |
| MAPE | Mean absolute percentage error |
| Top of atmosphere insolation | |
| MBE | Mean bias error |
| Water vapour pressure | |
| MPE | Mean percentage error |
| Wind Speed |
References
- Wassie, Y.T.; Adaramola, M.S. Potential environmental impacts of small-scale renewable energy technologies in East Africa: A systematic review of the evidence. Renew. Sustain. Energy Rev. 2019, 111, 377–391. [Google Scholar] [CrossRef]
- Babatunde, O.; Akinyele, D.; Akinbulire, T.; Oluseyi, P. Evaluation of a grid-independent solar photovoltaic system for primary health centres (PHCs) in developing countries. Renew. Energy Focus 2018, 24, 16–27. [Google Scholar] [CrossRef]
- Olatomiwa, L. Optimal configuration assessments of hybrid renewable power supply for rural healthcare facilities. Energy Rep. 2016, 2, 141–146. [Google Scholar] [CrossRef] [Green Version]
- Ipsakis, D.; Voutetakis, S.; Seferlis, P.; Stergiopoulos, F.; Elmasides, C. Power management strategies for a stand-alone power system using renewable energy sources and hydrogen storage. Int. J. Hydrog. Energy 2009, 34, 7081–7095. [Google Scholar] [CrossRef]
- Samy, M.; Barakat, S.; Ramadan, H. Techno-economic analysis for rustic electrification in Egypt using multi-source renewable energy based on PV/wind/FC. Int. J. Hydrog. Energy 2019, 45, 11471–11483. [Google Scholar] [CrossRef]
- Mohammadi, K.; Shamshirband, S.; Kamsin, A.; Lai, P.; Mansor, Z. Identifying the most significant input parameters for predicting global solar radiation using an ANFIS selection procedure. Renew. Sustain. Energy Rev. 2016, 63, 423–434. [Google Scholar] [CrossRef]
- Olatomiwa, L.; Mekhilef, S.; Shamshirband, S.; Petković, D. Adaptive neuro-fuzzy approach for solar radiation prediction in Nigeria. Renew. Sustain. Energy Rev. 2015, 51, 1784–1791. [Google Scholar] [CrossRef]
- Kuo, P.H.; Chen, H.C.; Huang, C.J. Solar Radiation Estimation Algorithm and Field Verification in Taiwan. Energies 2018, 11, 1374. [Google Scholar] [CrossRef] [Green Version]
- Mauleón, I. Assessing PV and wind roadmaps: Learning rates, risk, and social discounting. Renew. Sustain. Energy Rev. 2019, 100, 71–89. [Google Scholar] [CrossRef]
- IRENA. Renewable Power Generation Costs in 2017; International Renewable Energy Agency (IRENA): Abu Dhabi, UAE, 2018. [Google Scholar]
- Ayodele, T.; Munda, J. Potential and economic viability of green hydrogen production by water electrolysis using wind energy resources in South Africa. Int. J. Hydrog. Energy 2019, 44, 17669–17687. [Google Scholar] [CrossRef]
- Allahvirdizadeh, Y.; Mohamadian, M.; HaghiFam, M.R. Study of energy control strategies for a standalone PV/FC/UC microgrid in a remote. Int. J. Renew. Energy Res. (IJRER) 2017, 7, 1495–1508. [Google Scholar]
- Saadi, A.; Becherif, M.; Ramadan, H. Hydrogen production horizon using solar energy in Biskra, Algeria. Int. J. Hydrog. Energy 2016, 41, 21899–21912. [Google Scholar] [CrossRef]
- Rezaei, M.; Mostafaeipour, A.; Qolipour, M.; Momeni, M. Energy supply for water electrolysis systems using wind and solar energy to produce hydrogen: A case study of Iran. Front. Energy 2019, 13, 539–550. [Google Scholar] [CrossRef]
- Mohamed, B.; Ali, B.; Ahmed, B.; Ahmed, B.; Salah, L.; Rachid, D. Study of hydrogen production by solar energy as tool of storing and utilization renewable energy for the desert areas. Int. J. Hydrog. Energy 2016, 41, 20788–20806. [Google Scholar] [CrossRef]
- Menad, C.A.; Gomri, R.; Bouchahdane, M. Data on safe hydrogen production from the solar photovoltaic solar panel through alkaline electrolyser under Algerian climate. Data Brief 2018, 21, 1051–1060. [Google Scholar] [CrossRef]
- Sigal, A.; Leiva, E.P.M.; Rodríguez, C. Assessment of the potential for hydrogen production from renewable resources in Argentina. Int. J. Hydrog. Energy 2014, 39, 8204–8214. [Google Scholar] [CrossRef]
- Contreras, A.; Guirado, R.; Veziroglu, T. Design and simulation of the power control system of a plant for the generation of hydrogen via electrolysis, using photovoltaic solar energy. Int. J. Hydrog. Energy 2007, 32, 4635–4640. [Google Scholar] [CrossRef]
- Yaniktepe, B.; Genc, Y.A. Establishing new model for predicting the global solar radiation on horizontal surface. Int. J. Hydrog. Energy 2015, 40, 15278–15283. [Google Scholar] [CrossRef]
- Kaur, A.; Nonnenmacher, L.; Pedro, H.T.; Coimbra, C.F. Benefits of solar forecasting for energy imbalance markets. Renew. Energy 2016, 86, 819–830. [Google Scholar] [CrossRef]
- Halawa, E.; GhaffarianHoseini, A.; Li, D.H.W. Empirical correlations as a means for estimating monthly average daily global radiation: A critical overview. Renew. Energy 2014, 72, 149–153. [Google Scholar] [CrossRef]
- Bocca, A.; Bergamasco, L.; Fasano, M.; Bottaccioli, L.; Chiavazzo, E.; Macii, A.; Asinari, P. Multiple-regression method for fast estimation of solar irradiation and photovoltaic energy potentials over Europe and Africa. Energies 2018, 11, 3477. [Google Scholar] [CrossRef] [Green Version]
- Feng, Y.; Cui, N.; Zhang, Q.; Zhao, L.; Gong, D. Comparison of artificial intelligence and empirical models for estimation of daily diffuse solar radiation in North China Plain. Int. J. Hydrog. Energy 2017, 42, 14418–14428. [Google Scholar] [CrossRef]
- Xue, X. Prediction of daily diffuse solar radiation using artificial neural networks. Int. J. Hydrog. Energy 2017, 42, 28214–28221. [Google Scholar] [CrossRef]
- Alsina, E.F.; Bortolini, M.; Gamberi, M.; Regattieri, A. Artificial neural network optimisation for monthly average daily global solar radiation prediction. Energy Convers. Manag. 2016, 120, 320–329. [Google Scholar] [CrossRef]
- Hussain, S.; AlAlili, A. A hybrid solar radiation modeling approach using wavelet multiresolution analysis and artificial neural networks. Appl. Energy 2017, 208, 540–550. [Google Scholar] [CrossRef]
- Gairaa, K.; Khellaf, A.; Messlem, Y.; Chellali, F. Estimation of the daily global solar radiation based on Box–Jenkins and ANN models: A combined approach. Renew. Sustain. Energy Rev. 2016, 57, 238–249. [Google Scholar] [CrossRef]
- Mousavi Maleki, S.A.; Hizam, H.; Gomes, C. Estimation of hourly, daily and monthly global solar radiation on inclined surfaces: Models re-visited. Energies 2017, 10, 134. [Google Scholar] [CrossRef] [Green Version]
- Fan, J.; Wang, X.; Wu, L.; Zhang, F.; Bai, H.; Lu, X.; Xiang, Y. New combined models for estimating daily global solar radiation based on sunshine duration in humid regions: A case study in South China. Energy Convers. Manag. 2018, 156, 618–625. [Google Scholar] [CrossRef]
- Yacef, R.; Mellit, A.; Belaid, S.; Şen, Z. New combined models for estimating daily global solar radiation from measured air temperature in semi-arid climates: Application in Ghardaïa, Algeria. Energy Convers. Manag. 2014, 79, 606–615. [Google Scholar] [CrossRef]
- Fan, J.; Wang, X.; Wu, L.; Zhou, H.; Zhang, F.; Yu, X.; Lu, X.; Xiang, Y. Comparison of Support Vector Machine and Extreme Gradient Boosting for predicting daily global solar radiation using temperature and precipitation in humid subtropical climates: A case study in China. Energy Convers. Manag. 2018, 164, 102–111. [Google Scholar] [CrossRef]
- Hussain, S.; Al-Alili, A. A new approach for model validation in solar radiation using wavelet, phase and frequency coherence analysis. Appl. Energy 2016, 164, 639–649. [Google Scholar] [CrossRef]
- Hassan, M.A.; Khalil, A.; Kaseb, S.; Kassem, M. Exploring the potential of tree-based ensemble methods in solar radiation modeling. Appl. Energy 2017, 203, 897–916. [Google Scholar] [CrossRef]
- Oyebode, O.; Stretch, D. Neural network modeling of hydrological systems: A review of implementation techniques. Nat. Resour. Model. 2019, 32, e12189. [Google Scholar] [CrossRef] [Green Version]
- Oyebode, O.; Ighravwe, D.E. Urban Water Demand Forecasting: A Comparative Evaluation of Conventional and Soft Computing Techniques. Resources 2019, 8, 156. [Google Scholar] [CrossRef] [Green Version]
- Oyebode, O. Evolutionary modelling of municipal water demand with multiple feature selection techniques. J. Water Supply Res. Technol. AQUA 2019, 68, 264–281. [Google Scholar] [CrossRef] [Green Version]
- Yorukoglu, M.; Celik, A.N. A critical review on the estimation of daily global solar radiation from sunshine duration. Energy Convers. Manag. 2006, 47, 2441–2450. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, L.; Deng, S.; Xu, W.; Zhang, Y. A critical review of the models used to estimate solar radiation. Renew. Sustain. Energy Rev. 2017, 70, 314–329. [Google Scholar] [CrossRef]
- Halabi, L.M.; Mekhilef, S.; Hossain, M. Performance evaluation of hybrid adaptive neuro-fuzzy inference system models for predicting monthly global solar radiation. Appl. Energy 2018, 213, 247–261. [Google Scholar] [CrossRef]
- Baser, F.; Demirhan, H. A fuzzy regression with support vector machine approach to the estimation of horizontal global solar radiation. Energy 2017, 123, 229–240. [Google Scholar] [CrossRef]
- Fan, J.; Chen, B.; Wu, L.; Zhang, F.; Lu, X.; Xiang, Y. Evaluation and development of temperature-based empirical models for estimating daily global solar radiation in humid regions. Energy 2018, 144, 903–914. [Google Scholar] [CrossRef]
- Khosravi, A.; Koury, R.; Machado, L.; Pabon, J. Prediction of hourly solar radiation in Abu Musa Island using machine learning algorithms. J. Clean. Prod. 2018, 176, 63–75. [Google Scholar] [CrossRef]
- Khosravi, A.; Nunes, R.; Assad, M.; Machado, L. Comparison of artificial intelligence methods in estimation of daily global solar radiation. J. Clean. Prod. 2018, 194, 342–358. [Google Scholar] [CrossRef]
- Zou, L.; Wang, L.; Xia, L.; Lin, A.; Hu, B.; Zhu, H. Prediction and comparison of solar radiation using improved empirical models and Adaptive Neuro-Fuzzy Inference Systems. Renew. Energy 2017, 106, 343–353. [Google Scholar] [CrossRef]
- Akarslan, E.; Hocaoglu, F.O. A novel adaptive approach for hourly solar radiation forecasting. Renew. Energy 2016, 87, 628–633. [Google Scholar] [CrossRef]
- Rohani, A.; Taki, M.; Abdollahpour, M. A novel soft computing model (Gaussian process regression with K-fold cross validation) for daily and monthly solar radiation forecasting (Part: I). Renew. Energy 2018, 115, 411–422. [Google Scholar] [CrossRef]
- Mohammadi, K.; Shamshirband, S.; Petković, D.; Khorasanizadeh, H. Determining the most important variables for diffuse solar radiation prediction using adaptive neuro-fuzzy methodology; case study: City of Kerman, Iran. Renew. Sustain. Energy Rev. 2016, 53, 1570–1579. [Google Scholar] [CrossRef]
- Wang, L.; Kisi, O.; Zounemat-Kermani, M.; Salazar, G.A.; Zhu, Z.; Gong, W. Solar radiation prediction using different techniques: Model evaluation and comparison. Renew. Sustain. Energy Rev. 2016, 61, 384–397. [Google Scholar] [CrossRef]
- Zou, L.; Wang, L.; Lin, A.; Zhu, H.; Peng, Y.; Zhao, Z. Estimation of global solar radiation using an artificial neural network based on an interpolation technique in southeast China. J. Atmos. Sol.-Terr. Phys. 2016, 146, 110–122. [Google Scholar] [CrossRef]
- Suk, H.I. An introduction to neural networks and deep learning. In Deep Learning for Medical Image Analysis; Elsevier: Amsterdam, The Netherlands, 2017; pp. 3–24. [Google Scholar]
- Teodorovic, D.; Janic, M. Transportation Engineering: Theory, Practice and Modeling; Butterworth-Heinemann: Oxford, UK, 2016. [Google Scholar]
- Majumdar, A. Soft Computing in Textile Engineering; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Babatunde, D.E.; Anozie, A.; Omoleye, J. Artificial Neural Network and its Applications in the Energy Sector—An Overview. Int. J. Energy Econ. Policy 2020, 10, 250–264. [Google Scholar] [CrossRef]
- Awodele, O.; Jegede, O. Neural networks and its application in engineering. In Proceedings of the Informing Science & IT Education Conference (InSITE), Macon, GA, USA, 12–15 June 2009; pp. 83–95. [Google Scholar]
- Livieris, I.; Pintelas, P. A Survey on Algorithms for Training Artificial Neural Networks; University of Patras: Patras, Greece, 2008; Volume 4. [Google Scholar]
- Nisbet, R.; Elder, J.; Miner, G. Handbook of Statistical Analysis and Data Mining Applications; Academic Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Shahin, M.A.; Jaksa, M.B.; Maier, H.R. State of the art of artificial neural networks in geotechnical engineering. Electron. J. Geotech. Eng. 2008, 8, 1–26. [Google Scholar]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Li, X.; Yin, M. Application of differential evolution algorithm on self-potential data. PLoS ONE 2012, 7, e51199. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Natarajan, U.; Sekar, M.; Palani, S. Prediction of surface roughness in turning operations by computer vision using neural network trained by differential evolution algorithm. Int. J. Adv. Manuf. Technol. 2010, 51, 965–971. [Google Scholar] [CrossRef]
- Olatomiwa, L.; Mekhilef, S.; Shamshirband, S.; Petkovic, D. Potential of support vector regression for solar radiation prediction in Nigeria. Nat. Hazards 2015, 77, 1055–1068. [Google Scholar] [CrossRef]
- Khorasanizadeh, H.; Mohammadi, K.; Goudarzi, N. Prediction of horizontal diffuse solar radiation using clearness index based empirical models; A case study. Int. J. Hydrog. Energy 2016, 41, 21888–21898. [Google Scholar] [CrossRef]
- Olatomiwa, L.; Mekhilef, S.; Shamshirband, S.; Mohammadi, K.; Petković, D.; Sudheer, C. A support vector machine–firefly algorithm-based model for global solar radiation prediction. Sol. Energy 2015, 115, 632–644. [Google Scholar] [CrossRef]
- Abdalla, Y.A. New correlations of global solar radiation with meteorological parameters for Bahrain. Int. J. Sol. Energy 1994, 16, 111–120. [Google Scholar] [CrossRef]
- Angstrom, A. Solar and terrestrial radiation. Report to the international commission for solar research on actinometric investigations of solar and atmospheric radiation. Q. J. R. Meteorol. Soc. 1924, 50, 121–126. [Google Scholar] [CrossRef]
- Bahel, V.; Bakhsh, H.; Srinivasan, R. A correlation for estimation of global solar radiation. Energy 1987, 12, 131–135. [Google Scholar] [CrossRef]
- Bakirci, K. Correlations for estimation of daily global solar radiation with hours of bright sunshine in Turkey. Energy 2009, 34, 485–501. [Google Scholar] [CrossRef]
- Ramedani, Z.; Omid, M.; Keyhani, A.; Shamshirband, S.; Khoshnevisan, B. Potential of radial basis function based support vector regression for global solar radiation prediction. Renew. Sustain. Energy Rev. 2014, 39, 1005–1011. [Google Scholar] [CrossRef]
- Yohanna, J.K.; Itodo, I.N.; Umogbai, V.I. A model for determining the global solar radiation for Makurdi, Nigeria. Renew. Energy 2011, 36, 1989–1992. [Google Scholar] [CrossRef]





| Author | Method | Input Parameters | Performance Metrics | Location |
|---|---|---|---|---|
| [19] | linear, second third order polynomial | , | MAPE, MABE, RMSE | Turkey |
| [23] | ELM, BPNN-GA, BPNN-RF, GRNN | , , max. , | RRMSE, MAE, RE, NS | China |
| [24] | BPNN-PSO, BPNN-GA | , M, , , , , | R, RMSE, MAE | China |
| [25] | ANN-spatial interpolation | , , d, , , , d, clear sky days, heating degrees day, , , M, rainy days | MAPE, NRMSE, MPBE | Italy |
| [26] | ANFIS, GRNN, MLP, NARX | , , , | , RMSE, MAPE, MBE | United Arab Emirates |
| [27] | ARMA, NANN | RMSE, nRMSE, MBE, nMBE, MPE, | Algeria | |
| [29] | Temperature-based models (TBM) | , , , | , RMSE, NRMSE, MBE, GPI | China |
| [30] | empirical models, BNN | , , T | RMSE, MBE, MAE, R | Algeria |
| [31] | EGB, SVM | T, R, | RMSE, MBE, MAE, | China |
| [32] | ANN, MLP-ANN, ANFIS, NARX-NN | , , , | MAPE, , RMSE | United Arab Emirates |
| [33] | GBB and RF | , , d, , sunshine fraction, diffuse fraction | MBE, RMSE, , | Middle East, North Africa |
| [39] | ANFIS-GA, ANFIS-PSO, ANFIS-DE | , , , , | MAPE, RRMSE, MABE, , RMSE, R | Malyasia |
| [40] | fuzzy regression functions-SVM | latitude, longitude, , , | RMSE, MAE | Turkey |
| [41] | TBM | , , , , , | , RMSE, NRMSE, MBE, GPI | China |
| [42] | SVR, RBFNN, MLFFNN FIS, ANFIS | , , T, | R, RMSE, MSE | Abu Musa Island |
| [43] | ANFIS, ANFIS-ACO, ANFIS-GA, ANFIS-PSO, GMDH, MLFFNN | M, , , , P, , , TOAI, , , D | , RMSE, MSE | Iran |
| [44] | ANFIS, TBM | , , , , , , P | , RMSE, MAE | China |
| [45] | TBM | RMSE, MBE | Turkey | |
| [46] | GPR -K-fold cross validation model | , , , D, , , , , , daily sea level | MAPE, RMSE, EF | Iran |
| [47] | ANFIS | solar declination angle, , , , , , , , , max , , | MAPE, MABE, RMSE, | Iran |
| [48] | MLP, GRNN, RBNN | , T, , , , | RMSE, MAE | China |
| [49] | ANN based on spatial interpolation | , , , , , , , , , | RMSE, MBE, | China |
| Statistical Parameters | ||||
|---|---|---|---|---|
| Training | ||||
| Minimum | 22.80 | 18.00 | 1.30 | 8.17 |
| Maximum | 37.10 | 33.70 | 8.40 | 22.82 |
| Mean | 31.63 | 21.83 | 5.56 | 16.35 |
| St. Dev | 2.84 | 1.33 | 1.44 | 2.86 |
| Skewness | −0.17 | 3.33 | −0.65 | −0.45 |
| Testing | ||||
| Minimum | 26.20 | 18.20 | 1.60 | 9.86 |
| Maximum | 36.60 | 23.70 | 7.60 | 20.52 |
| Mean | 31.58 | 21.42 | 5.27 | 16.41 |
| St. Dev | 2.80 | 1.14 | 1.37 | 2.80 |
| Skewness | −0.12 | −0.15 | −0.35 | −0.79 |
| Phase | RMSE | NSE | |
|---|---|---|---|
| Training | 1.3292 | 0.7838 | 0.7835 |
| Testing | 1.1967 | 0.8254 | 0.8134 |
| Model | RMSE | |
|---|---|---|
| SVR-Radial | ||
| Training | 1.141814 | 0.8425 |
| Testing | 1.905994 | 0.5877 |
| SVR-Polynomial | ||
| Training | 1.363988 | 0.7703 |
| Testing | 1.510218 | 0.7395 |
| ANFIS-PSO | ||
| Training | 1.1157 | 0.8463 |
| Testing | 1.8015 | 0.5666 |
| ANFIS-GA | ||
| Training | 1.2769 | 0.7987 |
| Testing | 1.7696 | 0.6354 |
| ANFIS-DE | ||
| Training | 1.3503 | 0.7748 |
| Testing | 1.601 | 0.6926 |
| ANFIS-ACO | ||
| Training | 1.3505 | 0.7748 |
| Testing | 1.5485 | 0.7313 |
| ANFIS | ||
| Training | 1.0699 | 0.8586 |
| Testing | 2.0628 | 0.5468 |
| Present Study (ANN-DE) | ||
| Training | 1.3292 | 0.7838 |
| Testing | 1.1967 | 0.8254 |
| Reference | Model | Country of Study | Number of Inputs | |
|---|---|---|---|---|
| [64] | Empirical | Bahrain | 5 | 0.780 |
| [65] | Empirical | not specified | 3 | 0.780 |
| [66] | Empirical | Bahrain | 3 | 0.790 |
| [67] | Empirical | Turkey | 3 | 0.780 |
| [68] | ANN | Iran | 7 | 0.799 |
| [68] | SVR-RBF | Iran | 7 | 0.790 |
| [68] | ANFIS | Iran | 7 | 0.808 |
| [69] | Empirical | Nigeria | 3 | 0.608 |
| Present study | ANN-DE | Nigeria | 3 | 0.825 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Babatunde, O.M.; Munda, J.L.; Hamam, Y. Exploring the Potentials of Artificial Neural Network Trained with Differential Evolution for Estimating Global Solar Radiation. Energies 2020, 13, 2488. https://doi.org/10.3390/en13102488
Babatunde OM, Munda JL, Hamam Y. Exploring the Potentials of Artificial Neural Network Trained with Differential Evolution for Estimating Global Solar Radiation. Energies. 2020; 13(10):2488. https://doi.org/10.3390/en13102488
Chicago/Turabian StyleBabatunde, Olubayo M., Josiah L. Munda, and Yskandar Hamam. 2020. "Exploring the Potentials of Artificial Neural Network Trained with Differential Evolution for Estimating Global Solar Radiation" Energies 13, no. 10: 2488. https://doi.org/10.3390/en13102488
APA StyleBabatunde, O. M., Munda, J. L., & Hamam, Y. (2020). Exploring the Potentials of Artificial Neural Network Trained with Differential Evolution for Estimating Global Solar Radiation. Energies, 13(10), 2488. https://doi.org/10.3390/en13102488