Aerodynamic Performance Analysis of a Building-Integrated Savonius Turbine

Abstract

The building-integrated wind turbine is a new technology for the utilization of wind energy in cities. Previous studies mainly focused on the wind turbines mounted on the roofs of buildings. This paper discusses the performance of Savonius wind turbines which are mounted on the edges of a high-rise building. A transient CFD method is used to investigate the performance of the turbine and the interaction flows between the turbine and the building. The influence of three main parameters, including the turbine gap, wind angle, and adjacent turbines, are considered. The variations of the turbine torque and power under different operating conditions are evaluated and explained in depth. It is found that the edge-mounted Savonius turbine has a higher coefficient of power than that operating in uniform flows; the average C_p of the turbine under 360-degree wind angles is 92.5% higher than the turbine operating in uniform flows. It is also found that the flow around the building has a great impact on turbine performance, especially when the turbine is located downwind of the building.

1. Introduction

Renewable energies have attracted increasing attention thanks to diminishing global fossil fuel reserves. Although favorable progress has been obtained over the past few decades in exploring commercial renewable energies such as wind energy, solar energy, and ocean energies, more work needs to be done on the development of renewable energies in cities. Wind flow around buildings provides one of the potentially low-cost renewable sources of energy in cities [1]. With sustainable development becoming the driving force for more and more new buildings, it is expected that environmentally-friendly buildings with integrated wind turbines will increase in number [2].

Unlike common wind turbines on farms, building-integrated wind turbines experience more complex wind flows with low mean wind speeds and high levels of turbulence [3]. In addition, both the speeds and directions of the wind flows around buildings are significantly affected by the urban environment. It is found that if a turbine is sited in the wrong location on the building, the power output of the turbine might decrease to zero, even when the wind is blowing strongly [4]. Therefore, comprehensive efforts have been made to investigate the wind flow distributions around buildings [5]. In previous studies, the roof shape is taken as the key parameter that influences the performance of roof-mounted wind turbines. Rafailidis [6] found that the wind flow and turbulence intensity at the roof level were strongly dependent on roof shape. Abohela et al. [7] investigated how wind flows were affected by the building shape, and they found that the flow was accelerated near the building and suggested some mounting locations of the wind turbine. They claimed that a roof-mounted turbine had the potential to produce 56% more power than a free stream turbine. Similarly, Bobrova [8] also investigated the locations of the acceleration effects over different roof shapes to take advantage of the increased wind speed, which contains more kinetic energy. Except for the building shape, wind direction also has significant effects on the flow around buildings and has been studied. Ledo et al. [3] studied wind flow around different roof shapes and under three wind directions to find the best location for the wind turbine. Abohela et al. [7] numerically studied the effects of some factors on the energy production and installation location of roof-mounted wind turbines, such as wind direction, roof shape, urban configuration, and building height.

Although the wind flows around buildings have been investigated extensively, only a few studies considered the performance of real wind turbines mounted on buildings. Larin et al. [9] stated the importance of integrated simulations which include both the building and the turbine and numerically studied the performance of a Savonius wind turbine horizontally-mounted on the roof of a building. They considered the effects of the mounting position, blade number, and the circumferential length of the wind turbine. They found that the power coefficient could be improved from 0.043 to 0.24 by choosing the optimal configuration.

In the roof wind energy generation applications, the Savonius vertical axis wind turbine (VAWT) offers an interesting alternative. The Savonius wind turbine is a common type of drag-type vertical axis wind turbine [10]. Savonius wind turbines have a simple structure, as shown in Figure 1, consisting of two to three arc-typed blades. Savonius wind turbines have many advantages over other types of wind turbines, such as: (1) the ability to work in complex turbulent flow fields [11]; (2) the ability to operate at low speeds and low noise emissions [12]; (3) good starting performance and high torque at startup [13]; and (4) a simple structure. However, the disadvantage of the Savonius wind turbine is that its power efficiency is lower than that of most lift-type wind turbines. The main factors affecting the performance of Savonius wind turbines are gap ratio, blade shape, blades number, overlap ratio, turbines stages, guide plates, end plates, and other accessories [14,15,16]. Blades are the most important part of Savonius wind turbines, and a lot of work has been done on optimizing the shape of the blades. Tian et al. [10] introduced an optimization procedure of a modified Savonius blade. Kerikousab and Thévenina [17] modeled the Savonius blade using twelve geometrical parameters and carried out optimization work using evolutionary algorithms. They found that the performance of the Savonius wind blade was improved by almost 15% at a TSR of 1.2. Similar work is also done by Chan et al. [18]. Kumar and Saini [19] studied the effect of the blade arc angle and blade shape factor on the performance of a twisted Savonius turbine. Sharma and Sharma [20] added a small multiple quarter blade to conventional Savonius blades and obtained a 13.69% increase in the coefficient of power.

It should be noted that most previous building-integrated wind turbine studies assumed that the wind turbines were mounted on the roof of the building [3,6,7,8,9]. This might reduce the complexity of mounting; however, the appropriate area on the roof is relatively small, leading to a small amount of the total wind energy. Nowadays, high-rise buildings are common in modern cities. In addition to the roofs, the side edges of high-rise buildings also provide ideal positions for mounting wind turbines, as shown in Figure 1. Considering that the performances of wind turbines in this new configuration has not yet been investigated in-depth, this paper aims to evaluate the performances of the edge-mounted wind turbines under different flow conditions with a CFD method. Detailed reviews of the CFD techniques on modeling the wind flow around a building were presented by Toja-Silva et al. [5] and Larin et al. [9].

In the simulation of flow around buildings, the atmospheric boundary layer (ABL) is often defined, as illustrated in Figure 1. In a simplified ABL, the velocity of wind changes with height approximately following a power law [9]. Some researchers also presented more accurate and complex models of the ABL profiles [21,22]. Due to the non-uniform velocity in the ABL, the computational domains for the CFD analysis of buildings are relatively large with a vertical dimension of approximately 5 times that of the building height [5], leading to a great number of grid elements and a high computing time cost. Figure 1 shows three different patterns of the wind flows around a high-rise building, including the top flow, the side flow, and the ground flow. The top flow locates near the roof of the building, where the flow blows over the roof and forms an accelerated area above the roof. It is worth noting that previous roof-mounted wind turbines were designed mainly to utilize the top flow [9]. The ground flow locates near the base of the building and is caused by the difference in velocity near the ground and the block effect of the building. The side flow locates in the middle of the building, where the upstream flow is impeded by the building and passes to the two sides of the building. It is easy to understand that the side flow covers a greater area of the building than the other two flow patterns if the building is tall enough. This suggests that the wind energy potential is high in the side flow for tall buildings.

The building-integrated wind turbine is a new technology for the utilization of wind energy in cities. Previous studies mainly focused on the wind turbines mounted on the roofs of buildings. This paper discusses the performance of Savonius wind turbines, which are mounted on the edges of a high-rise building. In this study, the effect of three main parameters, including turbine gap, wind angle, and adjacent turbines on wind turbine performance are considered. First, mesh-independent verification and verification of CFD theory were performed. Then, a series of numerical simulations are performed for each parameter under different geometric characteristics. Finally, the impact of each parameter on the performance of the wind turbine was evaluated.

Highlight:

• The average power of the turbine decreases with increasing turbine gap.
• The average C_p of the turbine under 360-degree wind angles is 0.4256.
• Adjacent turbines directly leads to a decrease in the velocity of flow upstream of the turbine.

2. Problem Description

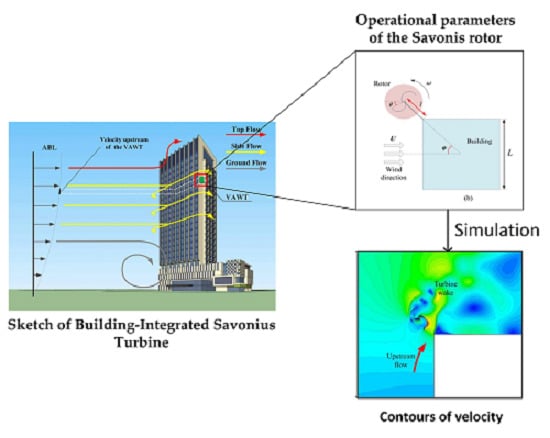
2.1. Parameter Definition

This paper deals with the CFD simulations of the edge-mounted wind turbines on a high-rise building. Before the modeling procedure, two assumptions are made to simplify the numerical model. These assumptions are reasonable for tall buildings:

(1)

The building is tall enough so that the vertical velocity components of the side flow is zero.

(2)

The height of the wind turbine is negligibly small compared with that of the building, hence the velocity of the flow upstream of the turbine can be treated as uniform.

Under the above two assumptions, the numerical model can be simplified with two-dimensional inflow. The VAWT considered here is a typical Savonius wind turbine. The structural parameters of the Savonius turbine are shown in Figure 2a, where D represents the rotor diameter, d represents the chord length of the blade, r represents the radius of the semicircle blade, and S represents the length of two blades’ overlap.

The building model is simplified as a square with a length of L. The turbine is designed to be placed on the corners of the building. Therefore, the position of the turbine can be defined by the gap between the center of the turbine and the corner of the building, l. Other operational parameters of the Savonius turbine are also shown in Figure 2b. U is the velocity of the upstream wind flow. φ is the wind angle defined by the angle between the wind direction and the line from the center of the building to the center of the turbine. ω is the rotation velocity of the turbine. θ is the azimuth angle of the blade, with zero angle obtained when the chord is parallel to the wind direction.

The specific values of both the structural and the operational parameters are provided in

Table 1. Parameters of the building-integrated VAWT.

Parameter	Value	Parameter	Value
D	0.91 m	U	7 m/s
d	0.50 m	l	variable
r	0.25 m	φ	variable
S	0.09 m	ω	variable
L	15.00 m	θ	variable

. It should be noted that the Savonius turbine in this paper has the same structural parameters as that previously tested in a wind tunnel [23]. By doing this, the simulation results could be easily compared with the experimental data.

2.2. Coefficients for Performance

Generally, the performance of a Savoius wind turbine is characterized by the change of the torque coefficient (C_m) and power coefficient (C_p) with the tip speed ratio (TSR). TSR, C_m and C_p can be obtained as follows:

$$TSR=\frac{\omega D}{2U}$$

(1)

$$C_m=\frac{4M}{\rho H{U}^2{D}^2}$$

(2)

$$C_p=\frac{P}{0.5\rho HD{U}^3}=C_m\cdot TSR$$

(3)

where M represents torque received by the blade and P represents power. Due to the two-dimensional assumption, the unit height H = 1 m is used.

2.3. Simulation Cases

This study focuses on investigating the performances of the building-integrated turbines with three key factors taken into consideration, including the turbine gap, the adjacent turbines, and the wind direction. Therefore, the simulation cases are divided into three groups, as listed in

Table 2. Simulation cases.

Group	Key Factors	l	φ	Number of Turbines	TSR
1	Turbine gap	0.75 D–2.00 D	45°	1	0.4–2.0
2	Adjacent turbines	1.00 D	45°	4	0.4–2.0
3	Wind direction	1.00 D	0°–360°	4	0.4–2.0

. It has been found that the rotation direction could affect the performance of the building-integrated VAWT [7]. However, in this paper, due to the symmetry of the building structure, the rotation direction of the turbine is related to the wind angle. For example, turbines at φ = 45° and φ = 315° rotating with the same direction can be treated as counter-rotating turbines at φ = 45°. Therefore, the turbines in the simulations all rotate counterclockwise.

3. Numerical Method

To evaluate turbine performance, transient CFD simulations were performed for each case listed in Table 2. As vertical flow is ignored and calculation time is taken into account, a two-dimensional simulation is used. Two-dimensional simulations are proven to be suitable for Savonius wind turbine simulation in previous studies [10,24,25]. In addition, in order to verify the numerical model, the results obtained from the numerical simulation will be compared with the experimental data.

3.1. Computational Domains and Grid Generation

Figure 3 provides the schematic of the overall domain, where four Savonius turbines are located near the corners of the building. Computational domain includes one fixed subdomain and four rotating subdomains. Air is assumed to be an incompressible fluid. The inlet is set to flow uniformly at a speed of 7 m/s. The outlet is a pressure outlet with a relative atmospheric pressure of 0 Pa. The top and bottom walls have symmetrical boundary conditions. No-slip boundary conditions are applied to the blade. Interface boundary conditions are set where the stationary domain and the rotating domains overlap. It is worth noting that under the inflow conditions of the calculation domain, the fluctuation of natural wind is not considered, and the given speed is uniform. In the simulation, the Reynolds number around the building is 1.3 $\times$ 10⁷.

The entire computational domain is discretized with quadrilateral elements, and the grids around the rotor and buildings are encrypted. The prism layer grid element is applied to the surface of the blades and buildings, and the y + value of the first layer grid is guaranteed to be about 1 to be suitable for the SSTk-ω turbulence model. The sliding grid method was used in this study, and the time step was set to the time when the rotor was rotated by 1 degree. The details of the computational domain mesh and local mesh are shown in Figure 4.

3.2. Numerical Method Validation

The case of l = 1.5 D, φ = 45°, and TSR = 1 is selected for convergence analysis. The change of the Cm of the blade and the rotor with the rotation angle is shown in Figure 5. It can be seen that after 7 rotation cycles, the Cm curve has basically converged. Therefore, it is reasonable for the calculation time for each case to last more than 15 cycles and to use the coefficient in the last cycle to evaluate the performance of the turbine.

Further, the contours and vectors of velocity at the last simulation step are provided in Figure 6 to more intuitively show the flow structures around the turbine and the building. It can be seen from Figure 6 that there exist several typical characteristics in the flow:

(1)

Stagnation: the stagnation point on the surface of the building with zero velocity.

(2)

High-Velocity Region: regions around the two sides of the building where the flow is deflected and accelerated.

(3)

Low-Velocity Region: regions between the High-Velocity Region and the sides of the building where small side vortices exist and the velocity is decreased.

(4)

Wake Vortices: vortices periodically shed from the corners of the building which have significant effects on the flow near the rear surface of the building.

A mesh independence verification study is conducted using three meshes with different node densities (82,000/103,000/136,000 elements). The verification simulations are conducted at l = 1.5 D, φ = 45$°$ and TSR = 1. The mesh independence is tested by comparing the torque of a single rotor for different numbers of mesh, and the result is shown in Figure 7. It can be seen that the curves of C_m are close to each other for different node densities. Accordingly, the mesh with approximately 103,000 elements can predict the performance of the rotor with sufficient accuracy, and with the change of the number of grids, there is no obvious change in the speed in sections with high gradients close to the turbine. Therefore, the grid resolutions of the meshes in the following simulations will be kept the same with the above verification case. It should be noted that the element number of the mesh with four turbines is larger due to the increased number of rotation domains.

To verify the CFD method, the C_m and C_p of the Savonius turbine were compared with wind tunnel test data [23]. To ensure the same verification conditions, the building is removed from the computational domain, leaving only the turbine. The turbine model selected in this paper has the same dimensions as that tested in the wind tunnel. Figure 8 suggests that the predicted C_m and C_p are in good agreement with the experimental data. As shown in the figure, three different turbulence model verifications are used in this paper. It can be seen from the figure that the turbulence model SSTk-ω has the smallest difference from the experimental data. The SSTk-ω method slightly underestimates the results at TSR = 0.6. The peak C_p from the CFD method is 0.2211, which is 2.6% lower than the experimental data. Therefore, it is acceptable to use the proposed CFD method to predict the performance of Savonius turbines.

4. Results and Discussion

In order to study the performance characteristics of the building-integrated Savonius turbines and to reveal the flow coupling mechanism between the building and the turbines, the simulation results are respectively discussed from three aspects: the turbine gap (l), adjacent turbines, and wind direction (φ). It is worth noting that the local velocity at the corner of the building is different from the velocity at the entrance. In order to make it easier to make a more intuitive comparison of turbine performance, the C_p coefficient of the turbine uniformly uses the uniform flow rate at the inlet. However, the velocity distribution at the corner of the building with different wind directions is shown in Figure 9.

4.1. Effects of Gap on the Performance of the Turbine

The turbine gap has a great influence on the flow between the building and the turbine, so the performance of the turbines with different turbine gaps is firstly studied. The simulated turbine is placed at a wind angle of φ = 45° and at different gaps (l = 0.75 D to 2.00 D). Figure 10 presents the averaged C_p of the turbine at four different gaps. As can be seen from Figure 10, the coefficients of power of all the turbines increase first and then decrease with increasing TSR. The power curve can be roughly divided into two intervals. When TSR < 0.8, the power curves of the four turbines are almost overlapped, indicating that the installation position has no obvious effect on the output power of the turbine. When TSR > 0.8, the power decreases significantly as the mounting position increases. It should be noted that the maximum C_p of the building-integrated turbine, 0.7390 at l = 0.75 D and TSR = 1.2, is 234.4% higher than the Savonius turbine operating in uniform flows (0.2211 in Figure 8).

To illustrate the effect of the turbine gap on the dynamic performance of the turbine, the instantaneous coefficients of torque on a single blade at different turbine gaps are given in Figure 11. During a rotation cycle, the blade torque experiences one positive and one negative intervals with peak values obtained at 120° and 300°, respectively. In the positive torque interval, the influence of the turbine gap on the torque is significant. The smaller the turbine gap, the larger the positive torque on the blade, which leads to the increase of the power. In the negative torque interval, the turbine gap has less effect on torque, and the torque increases slightly as the turbine gap increases.

Table 3. The position at which the torque coefficient falls to zero.

Turbine Gap	Position at Cm = 0
0.75 D	30.4° and 218.6°
1.00 D	25.8° and 218.3°
1.50 D	16.2° and 210.7°
2.00 D	7.40° and 201.5°

shows the position of the turbine when the torque coefficient falls to zero under different gaps. It can be seen from the table that as the gap of the turbine decreases, the position of the turbine when the torque coefficient falls to zero is also delayed.

To further illustrate the effect of turbine position on the blade torque, the contours of velocity near the turbines at θ = 120° and at different installation positions are shown in Figure 12. As marked in the figure, the flow fields around the turbines have similar flow structure at different gaps. The biggest difference occurs in the Jet Flow and the Recovery Flow. The Jet Flow is the result of the upstream free flow that is deflected by the building and flows through the gap between the building and the turbine. The Recovery Flow is the flow on the convex side of the blade that flows from the tip to the root of the blade and covers most of the area of the convex side. As can be seen from Figure 12, the width of the Jet flow increases with the turbine gap, but its velocity decreases. The velocity of the Recovery Flow decreases with the increased turbine gap, mainly because of the weakened Jet Flow.

The change of the intensity of the Jet Flow and the Recovery flow is the main reason for the variation of the blade torque. The pressure distributions on the blades at θ = 120° are presented in Figure 13, where the horizontal axis is the dimensionless blade chord. With the increase of the turbine gap, the Jet Flow is weakened, and the pressure on the concave side of the blade decreases. The pressure on the convex side of the blade is negative because of the Recovery Flow and the pressure increases with the weakened Recovery Flow. The changes of pressure on the two sides of the blade lead to a decrease in the total torque of the blade.

4.2. Effect of Adjacent Turbines on the Performance of the Turbine

In the previous subsection, a single turbine was used to study the effect of the turbine gap. However, in the case of engineering applications, it is likely that multiple wind turbines will be installed on the four corners of the building. The adjacent turbines will inevitably interact with each other in both wind flow and power. Therefore, the influence of adjacent turbines on the turbine performance needs to be analyzed.

In this section, four turbines are placed on the four corners of the building with the same turbine gap of l = 1.00 D, and the turbine at the wind angle of φ = 45° is chosen and compared with that individually installed at the same wind angle. Figure 14 shows the coefficients of power of the two turbines. Both curves follow the same trend and obtain the peak value at TSR = 1.0. The maximum C_p for multi-turbines is 0.4319, and is 29.2% lower than that of a single turbine. Even so, it is still much higher than that of the turbine rotating in uniform wind flows.

To illustrate the effect of the adjacent turbines on the dynamic performance of the turbine, the instantaneous coefficients of torque on a single blade are shown in Figure 15. During the whole rotating cycle, the positive torque is obviously decreased, while the negative torque is slightly increased due to the influence of the adjacent turbines.

The changes in the power and torque in Figure 14 and Figure 15 are the result of the changed flow. Figure 16 shows the contours of velocity for both the single turbine and the multi-turbines. The wind angle φ = 45° corresponds to the turbine on the upper left corner. It is clear that a stagnation point locates in front of the building. By comparing the velocity contours in the two cases, it is found that the position of the stagnation point is shifted upward and closer to the turbine (φ = 45°) in the case of multi-turbines. This directly leads to a decrease in the velocity of flow upstream of the turbine, as can be seen clearly in the zoom-in figure. The decrease of the upstream velocity directly leads to the reduction of turbine power and torque.

4.3. Effect of Wind Angle on the Performance of the Turbine

It is known that the flow around the building has different patterns under different wind directions. Because the turbines are mounted on the corners of the building, the wind angle can significantly affect the performance of the turbine. In this study, the performance of the turbine is evaluated under different wind angles varying from 0° to 337.5° with an interval of 22.5°. In the simulation cases, four turbines are placed at the corners of the building, so four sets of results can be obtained from each simulation.

Table 4. The maximum C_p and optimal TSR at each wind angle.

Wind Angle (°)	Maximum Cp	Optimal TSR	Wind Angle (°)	Maximum Cp	Optimal TSR
0	0.0131	0.4	180	0.0625	0.8
22.5	0.1577	0.4	202.5	0.3469	0.8
45	0.4319	1	225	0.1025	0.6
67.5	0.8689	1.2	247.5	0.4042	0.4
90	0.6187	1.4	270	0.8692	1.4
112.5	0.3306	0.4	292.5	1.2093	1.4
135	0.1388	0.6	315	0.7489	1.6
157.5	0.3229	0.8	337.5	0.1844	0.4

summarizes the optimal C_p of the turbine and the corresponding optimal TSR for different wind angles. It is clear that the maximum C_p and the optimal TSR vary with the wind angle. The maximum C_p is 1.2093, which is almost six times higher than the turbine rotating in uniform flows. In order to more intuitively display the trend of the maximum C_p and the optimal TSR, they are plotted in the polar figure in Figure 17. Figure 17a shows the schematic of the wind angle. The wind angle is zero when the wind direction is parallel to the line between the turbine and the center of the building.

Figure 17b presents the variation of the maximum C_p. It is clear that the turbine obtains lower power performance around φ = 0° and φ = 180°, whereas, at other wind angles, the power is higher. As a whole, the curve of power is approximately symmetrical about the 0° wind angle. Although the turbine has poor power performance under some wind angles, the averaged coefficient of power of the turbines under all wind angles is 0.4256, which is 92.5% higher than a turbine operating in uniform flows. This means that Savonius turbine has a better performance when installed on a building. The optimal TSR in Figure 17c shows a similar trend with the maximum C_p. It is interesting that the turbine presents a higher C_p at a higher optimal TSR. Considering the trend of the turbine power under 360-degree wind directions, the curve of C_p in the polar coordinates can be divided into four regions, which include the Front Region, the Left Side Region, the Right Side Region, and the Wake Region, and are marked with different colors in Figure 17b,c.

4.3.1. Front Region

The Front Region is where the wind angle is around 0° (−33.75° < φ < 33.75°). The turbine in this region exhibits the lowest coefficients of power, for example, the maximum C_p is 0.0131 at φ = 0°. Figure 18 presents the instantaneous coefficient of torque on a single blade at φ = 0° and TSR = 0.4. The maximum positive C_m is obtained at the blade azimuth angle of θ = 20°, with a value of 0.11, which is much lower than that presented in Figure 15, where the wind angle is φ = 45°.

The low performance of power and torque in the Front Region can be explained by the contours of velocity around the building, as shown in Figure 19. At φ = 0°, the building is symmetrical with respect to the direction of the incoming flow, thus forming a stagnant area in the forefront of the building. It can be seen from the figure that the turbine locates just in the stagnation region, where the flow velocity is very low. The low velocity leads to low performance of the turbine power and torque.

4.3.2. Left Side Region and Right Side Region

The Left Side Region corresponds to wind angles ranging from 33.75° to 123.75° and the Right-Side Region ranging from 236.25° to 326.25°. The turbine in these two regions has higher coefficients of power than the other two regions. To comparatively show the flow structures in these two regions, two typical wind angles are chosen, including φ = 67.5° and φ = 292.5°, which correspond to the highest C_p of the Left Side Region and the Right Side Region, respectively. Figure 20 presents the contours of velocity around the buildings at these two typical wind angles. It is found that the flow structures are almost the same, except that the velocity distributions are vertically symmetric due to the relative directions between the wind flow and the building.

Figure 21 presents the instantaneous coefficients of torque on a single blade at φ = 67.5° and 292.5° for TSR = 0.4. It is found that the trends of both torque curves are similar, with a positive peak value and a negative one, but the blade azimuth angles corresponding to the peak values are different. Take the positive torque peak as an example; the blade azimuth angle is 90° for φ = 67.5° and is 345° for φ = 292.5°. In addition, the maximum torque coefficient at φ = 292.5° is 23.73% higher than that at φ = 67.5° (2.19 vs. 1.77). The minimum torque coefficients are less affected by the wind angle.

Figure 20 indicates that turbines in the Left Side Region and the Right Side Region experience the same outside wind flow but rotate with opposite directions. Therefore, a deeper insight into the flow structures in these two regions may explain how the rotating direction affects the performance of the turbine. Figure 22 shows the velocity contours around the turbines at two typical blade azimuth angles, θ = 90° for φ = 67.5° and θ = 345° for φ = 292.5°, where the blades obtain the peak positive torque (Figure 21). It should be noted that the figure for φ = 292.5° is vertically flipped for a better comparison between these two cases. In the Left Side Region (φ = 67.5°), the blade is closer to the corner of the building and is mainly driven by the jet flow between the turbine and the building. In the Right Side Region, however, the blade is closer to the outfield flow and is mainly driven by the side accelerated flow. This implies that turbines in these two regions operate under different flow conditions. In both cases, a high-velocity flow is observed on the convex side of the blade (the Recovery Flow shown in Figure 12), causing a pressure drop on the convex surface and driving the blade. In addition, the Recovery Flow at φ = 292.5° is stronger than that at φ = 67.5°, possibly due to a smaller blockage of the upstream flow.

4.3.3. Wake Region

The Wake Region is where the wind angle is around 180° (123.75° < φ < 236.25°). The turbine in this region locates downstream of the building and is influenced by the vortices shed from the building. In the other three regions, the turbine is mainly affected by steady flows, so its torque reaches the oscillation convergence, as shown in Figure 5. However, in the wake region, the transient torque of the turbine presents a periodic fluctuation. To explain this, the turbine at φ = 157.5° is chosen, and its torque coefficient at TSR = 0.4 is shown in Figure 23. The simulation lasted for 60 rotating cycles to completely shown the periodic behavior of the torque. Although the torque curve oscillates per rotating cycle, its envelope curve periodically changes about every seven rotation cycles.

To explain the reason for the variation of the turbine torque in the wake region, the contours of vorticity and stream lines are used to show the flow structures around the building and the turbine. Figure 23 suggests that the turbine torque experiences three large periods from T = 39 to T = 59. In each large period, four cycles are chosen and presented in Figure 24. The turbine at φ = 157.5° is located on the upper right corner. The most obvious characteristic of the flow field is the vortices shed from the building. These vortices can be classified into three types: (1) Top Vortices (TVs), vortices shed from the top corner of the building with clockwise direction; (2) Bottom Vortices (BVs), vortices shed from the bottom corner of the building with counterclockwise direction; and (3) Wake Induced Vortices (WIVs), vortices caused by interactions between the TV, BV and the building. WIVs are much weaker than the TVs and the BVs.

The contours from T = 39 to T = 45 show the process of BVs shedding from the bottom corner of the building. At T = 39, a WIV and a BV can be observed beside the turbine. At this time, both vortices are too small to affect the turbine, so the turbine torque is low (Figure 23). The WIV and the BV start to merge at T = 41 and form a stronger BV downstream of the building. At T = 43, the BV covers the whole area of the right surface of the building, where the turbine is significantly influenced by the BV and obtains a high torque (Figure 23). As the flow further develops, the BV goes far from the turbine and has less effect on the turbine torque (T = 45). In short, the turbine torque between T = 39 and T = 45 is mainly affected by the development of the BV.

The contours from T = 46 to T = 52 show the process of TV shedding from the top corner of the building. Similarly, these four contours clearly show the process of how TV affects the turbine. The TV first rolls from the top surface of the building and moves near the turbine at T = 48, where the turbine obtains a high torque. Then, the TV moves downstream of the building. Because the TV and the BV have opposite rotating direction, the TV dissipates fast in the wake. In short, the turbine torque between T = 46 to T = 52 is mainly affected by the development of the TV. The contours from T = 53 to T = 59 show the same development process of BV as those from T = 39 to T = 45. This implies that the turbine torque during T = 53 to T = 59 is affected by the BV.

In summary, the building periodically shed vortices from the top and the bottom corners. These vortices significantly influence the performance of the turbine.

5. Conclusions

The performance of a Savonius wind turbine installed on the edges of a high-rise building is evaluated by a simplified two-dimensional transient CFD method. The influences of three main parameters, the turbine gap, wind angle, and adjacent turbines on the performance of the turbine are discussed. The variations of the turbine torque and power under different operating conditions are evaluated and explained in depth. The main conclusions of this paper are summarized as follows:

(1)

The average power of the turbine decreases with the increasing turbine gap, mainly because the gap changes the Jet Flow and Recovery flow. The maximum C_p of the building-integrated turbine, 0.7390 at l = 0.75 D and TSR = 1.2, is 234.4% higher than the Savonius turbine operating in uniform flows.

(2)

The maximum C_p for multi-turbines is 0.4319, and is 29.2% lower than that of a single turbine at l = 1.00 D and φ = 45°. Even so, it is still much higher than that of the turbine rotating in uniform wind flows.

(3)

Wind angle has a significant influence on the power output of the turbine. The average C_p of the turbine under 360-degree wind angles is 0.4256, which is 92.5% higher than the turbine operating in uniform flows. This means that Savonius turbine has better performance if installed on a building.

(4)

The turbine in the Front Region has the lowest coefficients of power. That is because the turbine locates just in the stagnation region, where the flow velocity is very low.

(5)

The turbine has higher coefficients of power in the Left Side Region and the Right Side Region, with a maximum C_p of 1.2093 obtained in the Right Side Region.

(6)

The turbine in the Wake Region is affected by the periodic vortices shed from the building corners and the transient torque shows a periodic fluctuation.

(7)

The influences of wind angle on the performance of the turbine are the most significant. When the turbine gap is smaller, it also improves the performance of the turbine. Compared to a single turbine, the effect of adjacent turbines on turbine performance is negative.