Forced Convection in Porous Media Using Al₂O₃ and TiO₂ Nanofluids in Differing Base Fluids

Abstract

The following work presents a numerical evaluation of the use of TiO₂ and Al₂O₃ nanofluids operating with ethylene glycol and water as base fluids—as well as an experimental evaluation of Al₂O₃-water nanofluid. Both numerical and experimental systems were tested and operated under various flow and heat transfer conditions, including four flow rates and three heat fluxes. When compared, the numerical schemes and experimental results showed deviation of under two degrees Celsius. This led the authors to conclude that the numerical scheme accurately reflected the experimental conditions. When all combinations of mixtures were compared numerically, it was found that ethylene glycol provided the highest average Nusselt number, while water offered significantly lower pumping requirements. When comparing nanoparticles, it was found that, in a carrying-fluid of water, TiO₂ had superior performance by approximately one percent.

1. Introduction

Nanofluids are a class of fluid composed of liquids used as base fluids, mixed with a set quantity of nanoparticles. These nanoparticles have differing physical properties from that of the base fluid aiming at enhancing the rate of heat removal. The concentration of the nanoparticles may be varied from 0.1% to up to 4%. Agglomeration, sedimentation and corrosive effects all play a role in the effectiveness of the cooling process. A large number of researchers have exaggerated the performance of this class of fluid. In the present study, the focus is first on conducting experiments to assess the importance of Al₂O₃ nanofluids and to determine the validity of the numerical model. Second, a numerical model is used to investigate the performance of TiO₂ nanofluid against an Al₂O₃ nanofluid. Lastly, the importance and influence of the base fluid in heat enhancement is investigated.

Azmi et al. [1] conducted a critical review concerning the effectiveness of using nanofluids for heat enhancement in forced convection. The authors discussed the importance of using ethylene glycol as a base fluid instead of water and a mixture of water and ethylene glycol (EG) as a base fluid. The performance of each nanofluid was discussed in detail. The authors’ motivation for this study was to discuss the importance of deviating from the usage of water as a base fluid toward the use of other base fluids such as e.g., and a mixture of e.g., and water. In their study they discussed different formulations to evaluate the physical properties whether, empirical or experimentally measured.

In order to determine accurate physical properties of nanofluid, Kumar Das et al. [2] managed to measure the physical properties of TiO₂ nanofluid in a water solution. The concentration of TiO₂ water based nanofluid varied between 0.1% to 2% for a range of temperatures from 20 °C to 60 °C. Different types of surfactants were used to achieve a stable solution. It was found that the viscosity of TiO₂-water nanofluid increased as the concentration of the solid nanoparticles increased and decreased with increasing temperature. However, the thermal conductivity was found to increase with the increasing concentration of nanoparticles and temperature. Another review study by Bashirnezhad et al. [3] discussing the experimental viscosity measurement for a variety of nanofluids showed similar findings to Kumar Das et al. as discussed above [2]. The authors discussed the effects of nanoparticle size in parallel to discussing the concentration and temperature effects.

Saghir et al. [4], Bayomy et al. [5], Alhajaj et al. [6]. Welsford et al. [7] and Delisle et al. [8] investigated experimentally and numerically the effectiveness of using Al₂O₃ nanofluid in water for a concentration varying between 0.1% to 0.5%. The forced convection flow through porous block or porous mini channels indicated a moderate heat enhancement of up to 6% when compared with water [5,7,8]. Duangthongsuk and Wongwises [9] conducted an experimental research project aiming at measuring the thermal conductivity and viscosity of TiO₂-water nanofluids. The concentration of Titanate varied between 0.2% and 2% vol. Their findings indicated an increase of the viscosity with nanoparticle concentration, further higher when compared to the base fluid which was water. However, their results were found to contradict the predicted values by other researchers.

In the same note, Pastoriza-Gallego et al. [10], conducted an experiment to measure the physical properties of Al₂O₃-EG nanofluids. The base fluid is more viscous and has lower conductivity when compared to water. The nanofluid exhibited a thermal conductivity enhancement of 19%, at a mass concentration of 25%, when compared to the base fluid as well as an increase in the viscosity when compared to the base fluid. Additional researchers [11,12,13,14,15,16,17,18] conducted measurements of physical properties of TiO₂ in water base fluids and in ethylene glycol base fluids. Contradicting values and results have been noticed.

Researchers conducted experimental measurement of heat enhancement in the laminar and turbulent flow regimes using TiO₂ in water base nanofluid [19,20,21,22]. Their findings indicate a heat enhancement up to 50%, thus, creating more confusion in the quality of enhancement to be expected with this type of nanofluid. Such conflicting reports encouraged the author to investigate the heat enhancement experimentally and numerically for a forced convection system operating in a porous block. Finally, some researchers focused on the application of the use of nanofluids [22,23,24,25,26]. Their findings confirmed an improvement in heat removal, while a reduction in cogeneration efficiency was observed. With such conflicting findings on one hand and exaggerated performance on the other hand, the present study aims to investigate the performance of the TiO₂ in water based and in e.g., based nanofluids for a different range of heating conditions. The study is structured as follows, in Section 2 the experimental description is presented in brief, followed by the numerical calculations in Section 3. Section 4 presents the results and discussions and the concluding remarks are made in Section 5. Advancing the study of nanofluids is an important task as it offers great potential for a plethora of heat transfer applications.

2. Materials and Methods

The present study employed the use of experimental techniques for the collection of data. The apparatus used in present was designed and built in such a way as to create isoflux conditions through the bottom of the test-section, combined with an isothermal fluid inlet [7]. The movement of the fluid through the system was controlled and measured using pumps, valves and a rotameter. The nanofluid evaluated herein, was Al₂O₃-water nanofluid with spherical nanoparticles. The thermal effects of the system were collected and measured using a total of ten T-type thermocouples. The inward heat flux was controlled and measured using a potentiometer, a voltmeter and an ammeter. These values were taken and used to define the total system performance as described in the following sections. When conducting an experiment, the test-section was prepared using the appropriate foam metal sample, and the system was primed and filled with the desired working fluid. The general inward heat flux was then set, and the system was given sufficient time to reach a steady operating state. The experimental apparatus is shown in Figure 1a, with a schematic of the test section shown in Figure 1b and a sample of the metal foam being studied shown in Figure 1d.

Measurement Error Analysis

Uncertainty analysis has been conducted and more details could be found in Bayomy et al [5]. The accuracy of the T-type thermocouples is known to be equal to 0.75%. The uncertainty of the flow meter used was 0.44%. The uncertainty of the flow meter and thermocouples was determined using the integrated calibration software from the data acquisition device’s manufacturer. The repeatability of the experiment is applied by ensuring steady state has been reached before taking the measurement. This is done as the inlet temperature is very important for the measured temperature along the direction of the flow. Maintaining a constant inlet temperature for the runs was not achieved due to the sensitivity of the system.

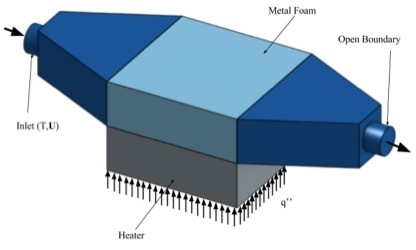
3. Finite Element Analysis

Navier–Stokes formulations in the fluid domain and the Darcy–Brinkman formulation in the porous domain is used. The discussed numerical domain and corresponding mesh is shown in Figure 1e.

3.1. Governing Equations and Boundary Conditions

The full Navier–Stokes equations combined with the Darcy–Brinkman formulation together with the continuity and energy equations are solved numerically using the finite element technique. The fluid inlet was governed by a combined isothermal and general inward velocity across the entrance. The outlet of the system was left free and open to both mass and energy flow to maintain conservation. All other surfaces were left as either thermal insulators or fluidic walls with no-slip. The boundary conditions of the present numerical model are shown in Figure 1c.

3.1.1. Mathematical Formulation

Combined fluid flow equations with the energy equation were solved numerically using the finite element method [5]. In particular, the momentum equations are as follow in different directions:

Momentum equation along x-direction

$${\mathsf{\rho }}_{\mathrm{nf}}\left(u\frac{\partial u}{\partial \mathrm{x}}+\mathrm{v}\frac{\partial u}{\partial \mathrm{y}}+\mathrm{w}\frac{\partial u}{\partial \mathrm{z}}\right)=-\frac{\partial \mathrm{p}}{\partial \mathrm{x}}+{\mathsf{\mu }}_{\mathrm{nf}}\left(\frac{{\partial }^{2}u}{\partial {\mathrm{x}}^2}+\frac{{\partial }^{2}u}{\partial {\mathrm{y}}^2}+\frac{{\partial }^{2}u}{\partial {\mathrm{z}}^2}\right)$$

(1)

Momentum equation along y-direction

$${\mathsf{\rho }}_{\mathrm{nf}}\left(u\frac{\partial \mathrm{v}}{\partial \mathrm{x}}+\mathrm{v}\frac{\partial \mathrm{v}}{\partial \mathrm{y}}+\mathrm{w}\frac{\partial \mathrm{v}}{\partial \mathrm{z}}\right)=-\frac{\partial \mathrm{p}}{\partial \mathrm{y}}+{\mathsf{\mu }}_{\mathrm{nf}}\left(\frac{{\partial }^2\mathrm{v}}{\partial {\mathrm{x}}^2}+\frac{{\partial }^2\mathrm{v}}{\partial {\mathrm{y}}^2}+\frac{{\partial }^2\mathrm{v}}{\partial {\mathrm{z}}^2}\right)$$

(2)

Momentum equation along z-direction

$${\mathsf{\rho }}_{\mathrm{nf}}\left(u\frac{\partial \mathrm{w}}{\partial \mathrm{x}}+\mathrm{v}\frac{\partial \mathrm{w}}{\partial \mathrm{y}}+\mathrm{w}\frac{\partial \mathrm{w}}{\partial \mathrm{z}}\right)=-\frac{\partial \mathrm{p}}{\partial \mathrm{z}}+{\mathsf{\mu }}_{\mathrm{nf}}\left(\frac{{\partial }^2\mathrm{w}}{\partial {\mathrm{x}}^2}+\frac{{\partial }^2\mathrm{w}}{\partial {\mathrm{y}}^2}+\frac{{\partial }^2\mathrm{w}}{\partial {\mathrm{z}}^2}\right)+{\mathsf{\rho }}_{\mathrm{nf}}\mathrm{g}$$

(3)

Continuity equation

The continuity equation for this simulation can be expressed as,

$$\left(\frac{\partial u}{\partial \mathrm{x}}+\frac{\partial \mathrm{v}}{\partial \mathrm{y}}+\frac{\partial \mathrm{w}}{\partial \mathrm{z}}\right)=0$$

(4)

Energy conservation equation

The energy equation is as follows

$${\left(\mathsf{\rho }\mathrm{cp}\right)}_{\mathrm{nf}}\left(u\frac{\partial \mathrm{T}}{\partial \mathrm{x}}+\mathrm{v}\frac{\partial \mathrm{T}}{\partial \mathrm{y}}+\mathrm{w}\frac{\partial \mathrm{T}}{\partial \mathrm{z}}\right)={\mathrm{k}}_{\mathrm{nf}}\left(\frac{{\partial }^2\mathrm{T}}{\partial {\mathrm{x}}^2}+\frac{{\partial }^2\mathrm{T}}{\partial {\mathrm{y}}^2}+\frac{{\partial }^2\mathrm{T}}{\partial {\mathrm{z}}^2}\right)$$

(5)

Here, ${\mathsf{\mu }}_{n\mathrm{f}}$, ${\mathsf{\rho }}_{n\mathrm{f}},{\mathrm{k}}_{n\mathrm{f}},{\mathrm{c}}_{\mathrm{p}}{}_{n\mathrm{f}}$ are the dynamic viscosity of the mixture, the density of the mixture, the thermal conductivity of the mixture and the specific heat of the mixture, respectively.

3.1.2. Darcy–Brinkman Model

Because the flow rate within the system is low and the porosity of the metal foam is 0.91, the Darcy–Brinkman equations are used for the analysis of the fluid behavior. The equations in three dimensions are as follows:

Darcy–Brinkman in x direction

$$\frac{{\mathsf{\mu }}_{\mathrm{nf}}}{\mathsf{\kappa }}u=-\frac{\partial \mathrm{p}}{\partial \mathrm{x}}+{\mathsf{\mu }}_{\mathrm{nf}}\left(\frac{{\partial }^{2}u}{\partial {\mathrm{x}}^2}+\frac{{\partial }^{2}u}{\partial {\mathrm{y}}^2}+\frac{{\partial }^{2}u}{\partial {\mathrm{z}}^2}\right)$$

(6)

Darcy–Brinkman in the y direction

$$\frac{{\mathsf{\mu }}_{\mathrm{nf}}}{\mathsf{\kappa }}\mathrm{v}=-\frac{\partial \mathrm{p}}{\partial \mathrm{y}}+{\mathsf{\mu }}_{\mathrm{nf}}\left(\frac{{\partial }^2\mathrm{v}}{\partial {\mathrm{x}}^2}+\frac{{\partial }^2\mathrm{v}}{\partial {\mathrm{y}}^2}+\frac{{\partial }^2\mathrm{v}}{\partial {\mathrm{z}}^2}\right)+{\mathsf{\rho }}_{\mathrm{nf}}\mathrm{g}$$

(7)

Darcy–Brinkman in the z direction

$$\frac{{\mathsf{\mu }}_{\mathrm{nf}}}{\mathsf{\kappa }}\mathrm{w}=-\frac{\partial \mathrm{p}}{\partial \mathrm{z}}+{\mathsf{\mu }}_{\mathrm{nf}}\left(\frac{{\partial }^2\mathrm{w}}{\partial {\mathrm{x}}^2}+\frac{{\partial }^2\mathrm{w}}{\partial {\mathrm{y}}^2}+\frac{{\partial }^2\mathrm{w}}{\partial \mathrm{z}}\right)$$

(8)

Moreover, the energy equation is written as follows;

$${\left({\mathsf{\rho }}_{\mathrm{nf}}{\mathrm{c}}_{\mathrm{p}}{}_{\mathrm{nf}}\right)}_{\mathrm{eff}}\left(u\frac{\partial \mathrm{T}}{\partial \mathrm{x}}+\mathrm{v}\frac{\partial \mathrm{T}}{\partial \mathrm{y}}+\mathrm{w}\frac{\partial \mathrm{T}}{\partial \mathrm{z}}\right)={({\mathrm{k}}_{\mathrm{nf}})}_{\mathrm{eff}}\left(\frac{{\partial }^2\mathrm{T}}{\partial {\mathrm{x}}^2}+\frac{{\partial }^2\mathrm{T}}{\partial {\mathrm{y}}^2}+\frac{{\partial }^2\mathrm{T}}{\partial {\mathrm{z}}^2}\right)$$

(9)

Here, $\mathsf{\kappa }$ is the permeability of the porous media and ${\left({\mathrm{k}}_{\mathrm{nf}}\right)}_{\mathrm{eff}}$ is the effective thermal conductivity of the mixture. The bottom surface of the first aluminum block was set at constant heat flux q”. Inlet temperature and velocity were applied at the flow entrance. Any remaining undefined surfaces were defined as thermal insulation for the heat transfer study, and as walls for the fluid mechanics simulation. Figure 1c displays the boundary conditions applied to the model. At the contact between the aluminum block and the experimental setup a thermal resistance layer was numerically applied The thermal conductivity of this thin layer is set equal to 0.6 W/(mK).

Table 1. Thermo-physical properties of fluids for different nanoparticle concentrations [1,11,14]. Reproduced from [1], Elsevier: 2016; Reproduced from [11], UMP: 2013; Reproduced from [14], Elsevier: 2014.

Fluid	${\mathsf{\mu }}_{\mathbf{n}\mathbf{f}}(\mathbf{kg}/\mathbf{m}·\mathbf{s})$	${\mathsf{\rho }}_{\mathbf{n}\mathbf{f}}(\mathbf{Kg}/\mathbf{m}$3)	$\mathbf{C}{\mathbf{p}}_{\mathbf{n}\mathbf{f}}(\mathbf{J}/\mathbf{Kg}·\mathbf{K})$	${\mathbf{k}}_{\mathbf{n}\mathbf{f}}(\mathbf{W}/\mathbf{m}·\mathbf{K})$	Pr (Prandtl Number)
Water	0.001002	998.2	4182	0.613	6.8358303
Ethylene glycol	0.0191	1127.966	2470.212	0.2463	191.56
0.5% Al2O3-0.995 Water	0.001032	1011.209	4121.17	0.62232483	6.8342
0.5% TiO2-0.995 Water	0.00144	1014	4111	0.775	7.64
0.5% TiO2-0.995 Ethylene glycol	0.0185	1143.2012	2437.7416	0.255	176.8558
0.5% Al2O3-0.995 Ethylene glycol	0.0209	1140.3262	2443.2952	0.26	196.4033

presents the physical properties used in this model. These physical properties were adopted from different publications where the data are measured experimentally. For more details on the numerical modeling, the reader is referred to reference [4].

3.2. Mesh Sensitivity Analysis

Figure 1f shows the variation of the Nusselt number (calculated 1 mm below the test section) with the number of elements. A mesh consisting of 300,000 elements is a good model to use on the computational side.

3.3. Convergence Criteria

In this particular model the default solver used was the segregated method. Convergence is reached if R_c for all the unknowns is below 1 × 10⁻⁶ in two successive iterations. The R_c criteria is shown as

$$R_c=\frac{1}{n· m}{\displaystyle \sum }_{i=1}^{i=m}{\displaystyle \sum }_{j=1}^{j=n}\left|\frac{\left(F_{i,j}^{s+1}-F_{i,j}^s\right)}{F_{i,j}^{s+1}}\right|$$

(10)

where F represents one of the unknowns, viz. u, v, w, p or T, where s is the iteration number and (i, j) represents the coordinates on the grid. For further information on the detailed solution method, the reader is referred to the COMSOL software manual (Version 5.2a, Newton, MA, USA) [26].

4. Results

In the present study, an attempt is made to investigate the importance of using aluminum oxide particles in water against Titanium oxide in water. This class of nanofluid will be investigated numerically for both nanofluids and experimentally for aluminum oxide nanofluid. The numerical prediction of TiO₂ will lead to an experimental measurement in future work. In the entire text the concentration of nanoparticle is set equal to 0.5% vol. The Al₂O₃ nanofluid mixture did not contain any surfactant and precipitation was not detected one month after preparing the solution in the lab. Different flow rates were applied, and different heat fluxes were considered. The inlet temperature may vary between different runs as indicated earlier due to the difficulty in maintaining an exactly constant inlet temperature for all experimental runs. In addition, two additional fluids were investigated, the first is distilled water (W) and the second is EG. The distilled water was investigated experimentally and numerically whereas EG was investigated numerically only.

4.1. Experimental Measurements

Two sets of experiments were conducted and the results were compared with the numerical ones. The first fluid is water where different heat fluxes were applied for different flow rates. The experiment was repeated with Al₂O₃-water nanofluid having a concentration of nanoparticles of 0.5% vol.

4.1.1. Water Working Fluid

In order to validate the numerical code, experiments have been conducted using water as the working fluid. The aim is to investigate experimentally the importance of heat enhancement when using water. Figure 2 presents a comparison between the experimental measurement and the numerical simulation of water flow through the porous block. As indicated earlier the temperature was measured 1 mm below the bottom surface of the porous block. Different heat fluxes were applied for different flow rates. Figure 2a shows the temperature variation for four different cases. For a flow rate of 0.22 USGPM (i.e., 1.3885 × 10⁻⁵ m³/s) the applied heat flux is 55,000 W/m² and the initial temperature was measured to be 17.8 °C. The comparison between the experimental measurement and the numerical calculation shows an excellent agreement at the entrance and afterwards the difference between the experiment and the numerical is around 1.3 °C. It is strongly believed that heat losses are more pronounced towards the end of the block. As the flow decreases, and in particular for a flow rate of 0.18 USGPM (i.e., 1.1364 × 10⁻⁵ m³/s) with an applied heat flux of 65,000 W/m² and inlet temperature of 18.05 °C. An increase in temperature profile is evident as a result of higher heat flux and lower flow rate. The agreement herein is very good with a maximum deviation between the experimental and numerical results of 1.1 °C. As the flow rate decreases to 0.15 USGPM (i.e., 9.463 × 10⁻⁶ m³/s) with a measured heat flux of 70,000 W/m² and inlet temperature equal to 17.8 °C. The temperature profile remains identical to the previous case, but with a higher temperature. Finally, as the flow rate reduces further to 0.1 USGPM (i.e., 6.31 × 10⁻⁶ m³/s) and measured heat flux applied at the plate of 80,000 W/m². The comparison indicates a very good agreement between experimental and numerical methods. A comment on the variation of the inlet temperature is that after each experiment, the cooling process takes place, but we are ultimately never able to reach the inlet temperature of the previous condition. By plotting the change in the temperature using the inlet temperature as a reference temperature one is able to do a good comparison between cases. Figure 2b presents identical cases, but at higher heat fluxes and inlet temperature conditions. As one may notice the range of temperature is higher than in the previous cases. At a flow rate of 0.22 USGPM, an excellent agreement between experimental and numerical measurement with a deviation of temperature of 1.5 °C was observed. The applied heat flux was 120,000 W/m² and the inlet temperature was measured as 19.91 °C. The temperature profile is identical for all cases, but for different temperature ranges. The heat flux applied for a flow rate of 0.18 USGPM, 0.15 USGPM and 0.1 USGPM were 145,000 W/m², 153,000 W/m² and 167,000 W/m², respectively. The inlet temperature for the three cases of 0.18, 0.15 and 0.1 USGPM flow rates were 20.26 °C, 19.86 °C and 20.66 °C, respectively.

4.1.2. Nanofluid Working Fluid

The experiment was repeated with nanofluid as a working fluid, 0.5%vol Al₂O₃ nanoparticles in distilled water. The physical properties of this nanofluid used in the numerical simulation are found in Table 1. Figure 3 presents the results for different flow rates with low heat fluxes and high heat fluxes similar to the previous cases. Figure 3a highlights the temperature variation at the same location of the thermocouples for three different flow rates of 0.22 USGPM, 0.18 USGPM and 0.15 USGPM, respectively. The corresponding heat fluxes and inlet temperature conditions are (67,000 W/m², 16.2 °C), (82,000 W/m², 16.5 °C) and (97,000 W/m², 16.55 °C), respectively. The temperature variation trend is similar to all the cases, but with different levels of intensity. An excellent agreement between the experimental and numerical data are observed with a maximum difference of 1.2 °C for a flow rate of 0.22 USGPM, increasing to 2.1 °C for a flow rate of 0.18 USGPM and 1.0 °C difference for a flow rate of 0.15 USGPM. However, one may compare the measured and computed data between the water based working fluid shown in Figure 2a and the nanofluid working fluid presented in Figure 3a at a flow rate of 0.22 USGPM. Although the heat fluxes applied in the nanofluid case is higher by 18% compared to the water working fluid case, one may notice a temperature increase by 17% in average. This acts as an indication that the nanofluid is capable of extracting more heat than the distilled water working fluid. Figure 3b displays the temperature variation with nanofluid as a working fluid with a flow rate of 0.22 USGPM and 0.18 USGPM corresponding to a heating condition of (155,000 W/m², 17.9 °C) and (185,000 W/m², 17.9 °C), respectively. A good agreement between the measured temperature and the computed one is achieved with a maximum temperature difference of 1.6 °C for the lower flow rate and less than 1 °C for the higher flow rate. One may conclude from these data that nanofluid is confirmed to be able to extract more heat than distilled water. Figure 4 displays the local Nusselt number measured experimentally and obtained numerically for the conditions in Figure 3. The Nusselt number is defined as the ratio of the heat flux multiplied by the characteristic length, being the diameter of the flow entrance, to the conductivity of the working fluid. The heat coefficient is known to be the ratio of the applied heat flux to the measured temperature minus the inlet temperature. A decrease in the local Nusselt number along the flow direction is obvious since the temperature increases along the flow direction. Even with small temperature differences, the reduction is amplified when the Nusselt number is calculated. Moreover, it is evident that as the flow rate increases the Nusselt number increases indicating better heat extraction.

4.2. Comparison of Heat Enhancement between TiO₂/Water Nanofluid and Al₂O₃/Water Nanofluid via Numerical Simulations

In order to investigate the effectiveness of using TiO₂/water nanofluid instead of Al₂O₃/water nanofluid it is useful to conduct some numerical modeling. In the past section, it has been demonstrated that the numerical code predicted accurately the temperature variation when compared with experimental measurements. Thus, purely numerical modeling will be used in this section to predict the TiO₂/water nanofluid performance. Table 1 presents the physical properties of 0.5% TiO₂/water nanofluid. Based on an extensive literature review, a contradiction in information of the physical properties of this class of nanofluid was observed. The data presented in Table 1 is found to be the best by the author’s knowledge. A comparison between TiO₂/water nanofluid and Al₂O₃/water nanofluid is conducted using the heat fluxes and the inlet temperatures obtained experimentally. Figure 5 presents the temperature variation 1 mm below the porous bottom surface as indicated in Figure 1b. Figure 5a shows the results for a flow rate of 0.22 USGPM, 0.18 USGPM, 0.15 USGPM and 0.1 USGPM corresponding to the heating conditions of (67,000 W/m², 16.2 °C), (82,000 W/m², 16.5 °C), (97,000 W/m², 16.55 °C) and (97,000 W/m², 16.55 °C), respectively. On may notice that the TiO₂/water nanofluid with 0.5% concentration provided a slightly improved heat enhancement when compared to Al₂O₃/water nanofluid. This average improvement is found to be 1%. The same comparison was repeated for high heat flux conditions and for similar flow rates of 0.22 USGPM, 0.18 USGPM, 0.15 USGPM and 0.1 USGPM. The corresponding heat condition is identical for all cases having a heating flux of 155,000 W/m² and an inlet temperature equal to 17.9 °C. At high heat flux conditions, the effectiveness of TiO₂/water nanofluid surpass the Al₂O₃/water nanofluid by less than 0.7%.

4.3. Effectiveness of Base Fluid in Nanofluid

It has been mentioned in the literature that different nanofluids having different base solutions can be employed. water is the most commonly used, but ethylene glycol has been used in the past as a cooling fluid and as such has been proposed. Interestingly when ethylene glycol is compared to water it is more viscous while also having lower conductivity and specific heat. This high viscosity creates higher shear stress and as such one may expect a larger pressure drop and high friction coefficient. It is believed that the high friction may give more heat absorption, but this needs to be checked. For this reason, Figure 6a shows the heat performance of water versus ethylene glycol in the absence of nanoparticles. Four different flow rates of 0.22 USGPM, 0.18 USGPM, 0.15 USGPM and 0.1 USGPM were used corresponding to a heating condition of (55,000 W/m², 17.8 °C), (65,000 W/m², 17.8 °C), (70,000 W/m², 17.8 °C) and (80,000 W/m², 17.8 °C), respectively. By reviewing the temperature distribution, with ethylene glycol, the Prandtl number is very high. Yet its performance in heat removal is lower than that of water. For example, at a flow rate of 0.15 USGPM, the water exceeds the heat removal by 7% in average over an ethylene glycol solution. Thus, one can conclude that ethylene glycol is not a good fluid to be used as a base fluid in nanofluid solutions. The model was repeated with high heat fluxes at similar flow rates. Under identical heating conditions of 155,000 W/m² and an applied inlet temperature of 17.8 °C, four different flow rates of 0.22 USGPM, 0.18 USGPM, 0.15 USGPM and 0.1 USGPM were applied. Figure 6b presents the temperature variation along the flow. It is evident that the performance of water over the ethylene glycol is substantial. For example, for a flow rate of 0.15 USGPM, water overperforms the ethylene glycol by an average of 10%. It is also important to notice that the shape of the temperature distribution is identical for both fluids.

4.4. Importance of Nanofluid with Base Fluid

With water heat performance exceeding ethylene glycol, our interest is shifted towards investigating two different nanofluids with ethylene glycol as a base solution. The two proposed nanofluids are Al₂O₃/EG and TiO₂/EG both having a 0.5%vol concentration of nanoparticles. Figure 7 presents the temperature variation for four different flow rates. The heating condition is identical for all cases with a heat flux of 155,000 W/m² and an inlet temperature of 17.9 °C. As shown in Figure 7 both nanofluids give identical performance. One may conclude that the base fluid herein is not meant for heat enhancement, but for augmenting the pressure drop effects.

4.5. Friction Factor and Pumping Power

It is important to investigate the friction factor as well as the pumping power needed of a water based nanofluid or ethylene glycol base nanofluid. The friction factor is defined as

$$f=0.5\frac{∆\mathrm{p}\times \mathrm{De}}{{\mathsf{\rho }}_{\mathrm{m}}{\mathrm{u}}^2\times \mathrm{L}}$$

(11)

where $∆\mathrm{p}$ is the pressure difference at the center of the block at the entrance of the flow to the porous block and at the exit of the flow from the block. The density of nanofluid is ${\mathsf{\rho }}_{\mathrm{m}}$, the length of the porous block is L and the entrance diameter of the pipe is De. The velocity at the center of the block along the flow is u. Figure 8a compares the friction coefficient between TiO₂/water nanofluid and Al₂O₃/water nanofluid for four different flow rates. By comparing the two nanofluids for the same flow rate it is evident that the friction factor for Al₂O₃ nanofluid is less than the friction factor for TiO₂ nanofluid. Moreover, regarding the nanofluid both have low friction factors This is mainly due to the fact that water is the base fluid for both mixtures. The pumping power is known to be the product of the velocity u by the pressure drop displayed in Figure 8b. It shows that nanofluid with TiO₂ nanoparticles requires higher pumping power than nanofluid with Al₂O₃ nanoparticles. Figure 9 displays the same calculation, but for ethylene glycol base fluid. All other conditions are identical to the previous case. Two important observations were made; the first is that the friction factor is greatly higher than the water base nanofluid and the aluminum oxide nanofluid requires higher pumping power. The friction factor displayed in Figure 9a shows a flat and constant friction factor with no variation along the flow direction. This is contrary to the previous case presented in Figure 8a where the friction is changing linearly along the flow rate, but with lower intensity. Figure 9b indicates that nanofluid with Al₂O₃ nanoparticles requires higher pumping power than nanofluid with TiO₂ nanoparticles.

One may summarize the findings by examining Figure 10a,b. In Figure 10a, the Nusselt number for all proposed fluid were calculated for a heat flux of 60,000 W/m² and inlet temperature of 20 °C for a flow rate of 0.15 USGPM. A higher Nusselt number for the ethylene glycol compared to water can be observed. In addition, the titanium oxide in ethylene glycol nanofluid has higher Nusselt number than aluminum oxide in ethylene glycol solution. This is an excellent indicator that nanoparticles with ethylene glycol can provide better heat removal than nanoparticles in water–based solutions. The rationale for such a finding is because nanofluids with water solutions provide a very low Nusselt number. Is it possible that this increase in the Nusselt number is driven by the increased interaction between the EG base fluid and the ligaments (higher viscosity causes a slower more thorough interaction between the fluid and ligament) allowing more absorption of energy before dissipation. Because the fluids are at constant flow rate the more viscous, the fluid is able to absorb more energy (and because of constant flow) while still exiting the system at the same time. It was observed that introduction of EG can show three times the performance of water–based fluids. Figure 10b display the friction factor at the same condition as Figure 10a. It is evident with high heat extraction one may need higher pumping power. A trade-off needs to be studied depending on the design requirements.

5. Discussion

The above study successfully evaluates and models the performance of four combinations of TiO₂ and Al₂O₃ nanofluids with water and ethylene glycol bases. The following summarizes the major findings of the present work:

• A numerical model was successfully adapted to recreate experimental conditions for Al₂O₃-water nanofluid at various operating conditions. The maximum difference found between the experimental and numerical results was found to be less than two degrees Celsius;
• When comparing ethylene glycol and water as heat transfer fluids operating within porous media, water was found to outperform the ethylene glycol by 10%;
• When comparing TiO₂ and Al₂O₃ nanoparticles suspended at 5% vol in water it was found that, at both high and low heat flux ranges, the TiO₂-water nanofluid had superior performance by around 1%;
• When all four combinations of nanofluids were compared it was found that the mixtures based on ethylene glycol outperformed those of water from the perspective of the Nusselt number. However, when pumping power was considered to be a key element, the highly viscous base fluid showed potential weakness.

In conclusion, the authors believe that a large conflict exists in the present literature surrounding the real enhancement found from using nanofluids. Furthermore, the authors believe that the enhancement shown by including nanoparticles in the working fluid is often over-stated and that the experimental results presented above show more closely which values are likely to be found. This substantially different result should be taken into consideration by future researchers when considering the application of nanofluids.