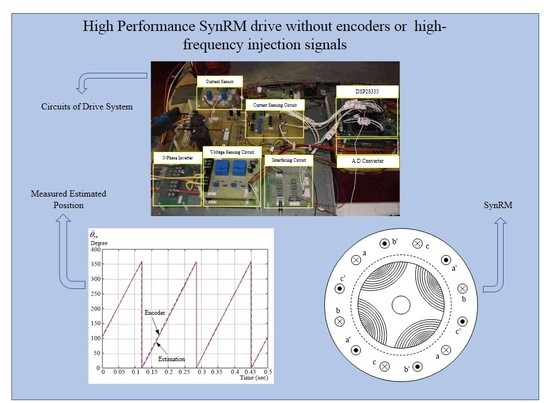
Simulation and Implementation of Predictive Speed Controller and Position Observer for Sensorless Synchronous Reluctance Motors
Abstract
:1. Introduction
2. Mathematical Model
3. Rotor-Position-Observer Design
4. Predictive-Controller Design
5. Implementation
6. Experiment Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bolognani, S.; Ortombina, L.; Tinazzi, F.; Zigliotto, M. Model sensitivity of fundamental-frequency-based position estimators for sensorless PM and reluctance synchronous motor drives. IEEE Trans. Ind. Electron. 2018, 65, 77–85. [Google Scholar] [CrossRef]
- Wei, M.Y.; Liu, T.H. A high-performance sensorless position control system of a synchronous reluctance motor using dual current-slope estimating technique. IEEE Trans. Ind. Electron. 2012, 59, 3411–3426. [Google Scholar]
- Varatharajan, A.; Pellegrino, G. Sensorless synchronous reluctance motor drives: A general adaptive projection vector approach for position estimation. IEEE Trans. Ind. Appl. 2020, 56, 1495–1504. [Google Scholar] [CrossRef]
- Tornello, L.D.; Scelba, G.; Scarcella, G.; Cacciato, M.; Testa, A.; Foti, S.; Caro, S.D.; Pulvirenti, M. Combined rotor-position estimation and temperature monitoring in sensorless, synchronous reluctance motor drives. IEEE Trans. Ind. Appl. 2019, 55, 3851–3862. [Google Scholar] [CrossRef]
- Senjyu, T.; Shingaki, T.; Uezato, K. Sensorless vector control of synchronous reluctance motors with disturbance torque observer. IEEE. Trans. Ind. Electron. 2001, 48, 402–407. [Google Scholar] [CrossRef]
- Lim, H.B.; Lee, J.H. The evaluation of online observer system of synchronous reluctance motor using a coupled transient FEM and Preisach model. IEEE Trans. Magnet. 2008, 44, 4139–4142. [Google Scholar]
- Vagati, A.; Pastorelli, M.; Franceschini, G.; Drogoreanu, V. Flux-observer-based high-performance control of synchronous reluctance motors by including cross saturation. IEEE Trans. Ind. Appl. 1999, 35, 597–605. [Google Scholar] [CrossRef]
- Tuovinen, T.; Hinkkanen, M. Adaptive full-order observer with high-frequency signal injection for synchronous reluctance motor drives. IEEE J. Emerg. Select. Top. Power Electron. 2014, 2, 181–189. [Google Scholar] [CrossRef] [Green Version]
- Tuovinen, T.; Hinkkanen, M.; Luomi, J. Analysis and design of a position observer with resistance adaption for synchronous reluctance motor drives. IEEE Trans. Ind. Appl. 2013, 49, 66–73. [Google Scholar] [CrossRef] [Green Version]
- Tuovinen, T.; Hinkkanen, M. Signal-injection-assisted full-order observer with parameter adaption for synchronous reluctance motor drives. IEEE Trans. Ind. Appl. 2014, 50, 3392–3402. [Google Scholar] [CrossRef] [Green Version]
- Awon, H.A.A.; Tuovinen, T.; Saarakkala, S.E.; Hinkkanen, M. Discreet-time observer design for synchronous reluctance motor drives. IEEE Trans. Ind. Appl. 2016, 52, 3968–3979. [Google Scholar] [CrossRef]
- Tuovinen, T.; Hinkkanen, M. Comparison of a reduced-order observer and a full-order observer for sensorless synchronous motor drives. IEEE Trans. Ind. Appl. 2012, 48, 1959–1967. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.K.; Yu, J.T.; Lai, Y.S.; Yu, H.C. Improved model-free predictive current control for synchronous reluctance motor drives. IEEE Trans. Ind. Electron. 2016, 63, 3942–3953. [Google Scholar] [CrossRef]
- Hadla, H.; Cruz, S. Predictive stator flux and load angle control of synchronous reluctance motor drives operating in a wide speed range. IEEE Trans. Ind. Electron. 2017, 64, 6950–6959. [Google Scholar] [CrossRef] [Green Version]
- Carlet, P.G.; Tinazzi, F.; Bolognani, S.; Zigliotto, M. An effective model-free predictive current control for synchronous reluctance motor drives. IEEE Trans. Ind. Appl. 2019, 55, 3781–3790. [Google Scholar] [CrossRef] [Green Version]
- Antonello, R.; Carraro, M.; Peretti, L.; Zigliotto, M. Hierarchical scaled-states direct predictive control of synchronous reluctance motor drives. IEEE Trans. Ind. Electron. 2016, 63, 5176–5185. [Google Scholar] [CrossRef]
- Lin, C.K.; Yu, J.T.; Lai, Y.S.; Yu, H.C.; Peng, C.I. Two-vector-based modeless predictive current control for four-switch inverter-fed synchronous reluctance motors emulating the six-switch inverter operation. IEEE Trans. Electron. Lett. 2016, 52, 1244–1246. [Google Scholar] [CrossRef]
- Ioannou, P.; Fidan, B. Adaptive Control Tutorial; SIAM: Philadelphia, PA, USA, 2006. [Google Scholar]
- Astrom, K.J.; Wittenmark, B. Adaptive Control, 2nd ed.; Addison-Wesly: New York, NY, USA, 1995. [Google Scholar]
- Maciejowski, J.M. Predictive Control with Constraints; Pearson Education Limited: London, UK, 2002. [Google Scholar]
- Rodriquez, J.; Corts, P. Predictive Control of Power Converters and Electrical Drives; Wiley: London, UK, 2012. [Google Scholar]
- Wang, L.; Chai, S.; Yoo, D.; Gan, L.; Ng, K. PID and Predictive Control of Electrical Drives and Power Converters Using MATLAB/Simulink; Wiley: Singapore, 2015. [Google Scholar]
- Toliyat, H.A.; Campbell, S. DSP-Based Electromechanical Motion Control; CRC Press: New York, NY, USA, 2003. [Google Scholar]
















© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.-H.; Ahmad, S.; Mubarok, M.S.; Chen, J.-Y. Simulation and Implementation of Predictive Speed Controller and Position Observer for Sensorless Synchronous Reluctance Motors. Energies 2020, 13, 2712. https://doi.org/10.3390/en13112712
Liu T-H, Ahmad S, Mubarok MS, Chen J-Y. Simulation and Implementation of Predictive Speed Controller and Position Observer for Sensorless Synchronous Reluctance Motors. Energies. 2020; 13(11):2712. https://doi.org/10.3390/en13112712
Chicago/Turabian StyleLiu, Tian-Hua, Seerin Ahmad, Muhammad Syahril Mubarok, and Jia-You Chen. 2020. "Simulation and Implementation of Predictive Speed Controller and Position Observer for Sensorless Synchronous Reluctance Motors" Energies 13, no. 11: 2712. https://doi.org/10.3390/en13112712
APA StyleLiu, T. -H., Ahmad, S., Mubarok, M. S., & Chen, J. -Y. (2020). Simulation and Implementation of Predictive Speed Controller and Position Observer for Sensorless Synchronous Reluctance Motors. Energies, 13(11), 2712. https://doi.org/10.3390/en13112712