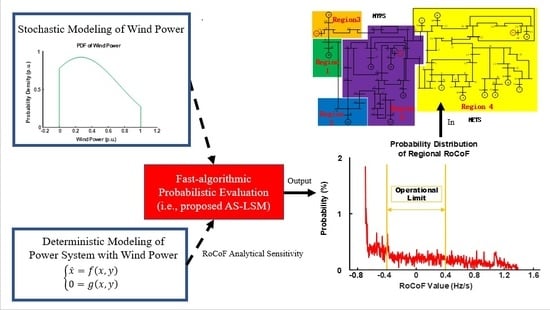
1. Introduction
The integration of renewable energy sources (RESs) brings an increasing number of stochastic disturbances into power systems [
1,
2,
3,
4] and meanwhile considerably reduces the system inertia [
5,
6,
7], which hence incurs higher rate of change of frequency (RoCoF) than ever before [
8,
9], and sometimes even serious incidents [
10]. The recent London blackout on 9 August 2019 has drawn wide attention, and the official investigation report [
10] indicates that a sudden reduction in the power output of the Hornsea offshore wind farm has worsened the RoCoF significantly, which further causes the enormous loss of both generations and demands. Hence, there is a pressing need to evaluate the impact of stochastic variation of RESs on the RoCoF in modern operational planning.
To accommodate the uncertainties brought by RESs, the safe operation of the system under the assumed “worst-case scenario” is guaranteed by reserving excessive conventional generation in real-time operation. However, the “worst-case scenario” where the uncertain disturbances of all the RESs reach maximum simultaneously rarely happens in a highly RES-penetrated power system because of spatiotemporal uncorrelation among the same or different types of the RESs in the network. For different types of RESs, wind power plants often reach the maximal output in the night while the photovoltaic plants only generate during the daytime. For the same type of RESs located in different places, the correlation of their stochastic output can be quite low. Both factors above significantly reduce the occurrence probability of the simultaneous maximal output of renewable energy plants. Thereby, a two-dimensional evaluation including both the severity and the occurrence probability of the event could be more beneficial for the system planner to make a decision, which may further increase the allowed penetration level of RESs. There are two common approaches to achieve the two-dimensional evaluation mentioned above [
11,
12,
13,
14]. (1) Monte Carlo simulation (MCS), which aims to compute the probabilistic distribution of the concerned indices by generating a large number of random variables and thus, simulation results. In [
13], scenario-based simulation (SBS), similar to MCS, is proposed to calculate the maximal renewable energy penetration limits to maintain the frequency performance by considering numerous potential operational scenarios. The results from the SBS are accurate, but its calculation procedure is very time-consuming, which is normally regarded as a verification tool. (2) Analytical method, e.g., cumulant-based analytical method (CBM), calculates the distribution of the concerned indices based on the sensitivity and the series expansion. This method can comfortably accommodate arbitrary types of continuous or noncontinuous distribution and correlation of stochastic variables [
14], which is proven to be the most efficient and accurate way to conduct probabilistic small-signal stability analysis in [
15]. In [
16], a probabilistic assessment framework on system RoCoF is proposed based on the CBM for the operational planning of a power system with RESs. However, the calculation procedure of the CBM is very complicated and not easy to implement.
The system frequency response (SFR), as an overall performance of the system frequency, is aggregated by frequency responses of the individual generator [
17] and normally required to remain within a specific range set by the system operator [
18]. While the heterogeneity of different regional frequency responses would be more obvious because of the increasing penetration level of distributed RESs and uneven distribution of inertia sources, which cannot be simply revealed by an integrated SFR [
19,
20,
21]. Reference [
13] reports that regional RoCoF violates the given limits, whereas the system RoCoF operates safely after the disturbance, which demonstrates the necessity of regional RoCoF assessment. Moreover, the RoCoF at the disturbance instant (i.e., t = 0
+) is usually observed to be the worst RoCoF without any assistance from the system fast-acting control [
19,
22,
23,
24]. Hence, regional RoCoF deserves a careful investigation in the operational planning stage to avoid the potential risk of RoCoF violation.
Taking all the points above into consideration, the paper proposes a novel fast-algorithmic evaluation to efficiently determine the probabilistic distribution of regional RoCoF, which demonstrates a clear superiority over the time-consuming SBS and the complicated CBM. The main contributions of the paper are listed below accordingly:
1. By combining the analytical sensitivity (AS) of RoCoF and the linear sensitivity-based method (LSM), AS-LSM is proposed to calculate the RoCoF. AS can adequately reflect the essential relationship between the variation of RESs and the RoCoF. Together with AS, LSM enables the evaluation of the RoCoF considering a complex multi-RES environment by using a superimposing technique, which considerably facilitates the understanding and implementation.
2. The proposed AS-LSM can facilitate the calculation for the probabilistic distribution of regional RoCoF. As a combination of numerical and analytical methods for probabilistic computation, the AS-LSM has a higher computing efficiency compared with SBS and a more straightforward calculation procedure compared with CBM.
3. The proposed AS-LSM could determine the probabilistic distribution of regional RoCoF influenced by the correlation of wind speed distribution more accurately than AS-CBM (i.e., CBM based on AS).
The rest of the paper is organized as follows. In
Section 2, regional analytical sensitivity (AS) of RoCoF is derived based on the generator and network information. Based on the derived regional AS and the linear sensitivity-based method (LSM), regional RoCoF in a multi-RES penetrated power system is calculated by the proposed AS-LSM in
Section 3. Case studies are conducted in
Section 4 to verify the effectiveness and efficiency of the proposed method with consideration of different wind speed correlations. The conclusion is drawn in
Section 5.
4. Case Study
The effectiveness of the proposed AS-LSM is verified by SBS with 5000 times simulation, and AS-CBM is also applied to examine the probabilistic distribution of regional RoCoF for the first time because of its proven good performance on the probabilistic computation of system RoCoF [
16]. The benchmark system is selected as a modified IEEE 16-machine 68-bus system with three wind farms (WFs) connected to bus 29, 32, and 41 respectively in
Figure 4 partitioned by slow coherency identification method [
26]. The probabilistic distributions of Region 4 and Region 5 are selected as the focus of the paper since they are the areas that contain more than one single generator. There are two scenarios studied in this section, i.e., with and without the correlations of wind speed.
The base capacity of the system is 100MVA. The operational state of the system decreases to 50% of the original level (system load, generation, and corresponding inertia). The capacity of each wind plant is 6 p.u, and the steady output is 2 p.u. The penetration of wind energy is defined by the ratio of the capacity of the WFs over the system load in [
27], which is 19.7% in this section.
Based on the calculation procedure in
Figure 3, after information acquisition and the system partition, the regional ASs w.r.t the output of individual WF are calculated according to (14), and the results are represented in
Table 1. For system-level analysis, the system is equivalent to one generator without considering the “electric distance,” which is also proven by (14) when n equals g, and hence, the system AS w.r.t the output of different WFs are the same. However, there is a large difference among the AS of regional RoCoF w.r.t the output of different WFs due to the comprehensive influences from both “electric distance” and regional inertia. In details, the AS of Region 4 RoCoF w.r.t WF2 and 3 is small (i.e., 0.049267 and 0.004431), whereas the sensitivity w.r.t WF1 is relatively large (i.e., 0.294051), which is caused by different “electric distance.” Furthermore, the maximal and minimal ASs of all regional RoCoFs w.r.t WF1 are 0.294051 and 0.000983 respectively, and the difference stems from the various regional inertia.
4.1. Scenario One (Uncorrelated Wind Speed)
The correlation between two wind power sources is closely related to their geographical distance, based on which correlation coefficient matrix
for
m grid-connected wind power sources is established [
28], and the wind speed distribution in [
29] is applied. In this scenario, the distances among each two WFs are assumed to be larger than 1200 km, which means there is no correlation among each WF, and hence the correlation matrix is a unit matrix.
Based on the AS in
Table 1, AS-LSM and AS-CBM are employed to calculate the probabilistic distribution of the system/regional RoCoF, which are examined by SBS in
Figure 5. The probabilistic density functions (PDFs) of the system, Region 4, and Region 5 RoCoF are exhibited in
Figure 5a–c, respectively. The operational limit of the RoCoF is concerned by the system operator, which is set ±0.4 Hz/s for demonstration [
16], and the detailed comparisons are given in
Table 2 and
Table 3.
The AS-LSM and AS-CBM perform well in computing the probabilistic distribution of the RoCoF in the system, Region 4, and Region 5 intuitively, as displayed in
Figure 5. Furthermore, it is also discovered that the shapes of the probabilistic distributions of the system RoCoF and the regional RoCoFs are different, but both methods could approach the trend, which is verified by the detailed result in both
Table 2 and
Table 3. The absolute errors of the probabilistic results by both AS-LSM and AS-CBM, as presented in
Table 3, reveal that the probabilistic distributions of system RoCoF calculated by both methods are relatively stable compared with that of regional RoCoFs. For example, the probabilistic result of Region 4 RoCoF can be estimated more accurately by AS-LSM than that by AS-CBM with less deviation (0.48% vs. 2.2733%). While the AS-CBM has a better performance than AS-LSM in calculating the probabilistic distribution of Region 5 RoCoF (0.1451% vs. 2.14%).
The computational time of each method are compared in
Table 4. Both AS-LSM and AS-CBM are more than 1000 times faster than SBS, while the AS-LSM is a little faster because of the simple calculation procedure, which avoids a large amount of computation on Gram-Charlier expansion.
4.2. Scenario Two (Correlated Wind Speed)
In this scenario, the correlation coefficient between WF2 and WF3 is set to be 0.8 (highly correlated) as (20).
The PDFs of RoCoF on the system and Region 4 are given in
Figure 6 and
Figure 7, respectively, for illustration, while the PDF of RoCoF associated with Region 5 is not given due to similar outcomes. The detailed probabilistic results and errors are also listed in
Table 5 and
Table 6, respectively.
Figure 6 illustrates the probabilistic distribution of system RoCoF carried out by SBS, AS-LSM, and AS-CBM. Compared with the real probabilistic distribution of system RoCoF in
Figure 5a, there are a few noticeable “impulses” (i.e., occurrence probability) at a few points on the horizontal ordinate (i.e., RoCoF value, including maximal/minimal system RoCoF), which increases the probability of the “worst-case scenario” and deserves careful consideration in operational planning. The most apparent “impulse” in
Figure 6 is the probability at the lowest RoCoF value, which is larger than the probability of the steady state (0 Hz/s). On the other hand, the total probability is 1, and this leads to a few decreases in the probabilities of other RoCoF values, which presents a smooth curve in
Figure 6. Both methods evaluate the system RoCoF well according to the detailed probabilistic results in
Table 5 and
Table 6.
As indicated in
Figure 7, the “impulses” still occur in the probabilistic distribution of regional RoCoF, and the curve is much smoother compared with that in uncorrelated wind speed situations. The probabilistic distribution of regional RoCoF obtained by SBS is not bell-shaped, which could be depicted by both methods effectively, while the AS-LSM performs better than AS-CBM owing to less deviation, i.e., 0.9% vs. 1.2902% in Region 4 RoCoF and 0.54% vs. 1.255% in Region 5 RoCoF as given in
Table 6.
5. Conclusions
The regional RoCoF is an important indicator for the safe operation of the power system, which needs to be carefully considered in operational planning. This paper proposes a fast-algorithmic assessment for the probabilistic distribution of regional RoCoF, which is more advantageous as it needs less time compared with SBS and provides a more straightforward calculating procedure than CBM. SBS validates the probabilistic results of both AS-LSM and AS-CBM with and without the consideration of wind speed correlation. Some important findings are summarized as follows:
(1) The probabilistic distributions of system RoCoF and regional RoCoF are different, i.e., bell-shaped vs. non-bell-shaped, which should be assessed separately. Both AS-LSM and AS-CBM can achieve the goal while AS-LSM has a better overall performance.
(2) When the wind speed correlation is considered, some evident “impulses” occur for the probabilistic distribution of both system and regional RoCoF as indicated by SBS. This phenomenon could be correctly reflected by both AS-LSM and AS-CBM, while AS-LSM performs better, which also demonstrates the flexibility and robustness of the proposed AS-LSM.
(3) The proposed AS-LSM converts a multi-disturbance problem into the superposition of a single-disturbance problem, which provides a more straightforward and convenient solution for their industrial implementation.