Models for Short-Term Wind Power Forecasting Based on Improved Artificial Neural Network Using Particle Swarm Optimization and Genetic Algorithms

Abstract

As sources of conventional energy are alarmingly being depleted, leveraging renewable energy sources, especially wind power, has been increasingly important in the electricity market to meet growing global demands for energy. However, the uncertainty in weather factors can cause large errors in wind power forecasts, raising the cost of power reservation in the power system and significantly impacting ancillary services in the electricity market. In pursuance of a higher accuracy level in wind power forecasting, this paper proposes a double-optimization approach to developing a tool for forecasting wind power generation output in the short term, using two novel models that combine an artificial neural network with the particle swarm optimization algorithm and genetic algorithm. In these models, a first particle swarm optimization algorithm is used to adjust the neural network parameters to improve accuracy. Next, the genetic algorithm or another particle swarm optimization is applied to adjust the parameters of the first particle swarm optimization algorithm to enhance the accuracy of the forecasting results. The models were tested with actual data collected from the Tuy Phong wind power plant in Binh Thuan Province, Vietnam. The testing showed improved accuracy and that this model can be widely implemented at other wind farms.

1. Introduction

Along with the requirements of the process of industrialization and modernization, together with increasing demands for economic growth and the exchange of goods and services across the globe, ensuring sufficient sources of energy has posed many challenges to countries worldwide. Traditional sources of energy such as coal, oil, and gas are increasingly exhausted, cause environmental pollution and uplift the greenhouse effects. To solve this problem, renewable energy has been widely encouraged with several alternative sources of energy being introduced and continuously developed. One of these is wind power, which is referred to as a clean source of energy with great potential for development. With the pace as it is now, wind power will soon occupy a large portion of the world energy market.

According to the Global Wind Report 2019 (GWEC), 60.4 GW of new installations brings the global cumulative wind power capacity up to 651 GW, as shown in Figure 1 [1].

Between 2010 and 2017, energy from wind power plants grew 3.3 times, from 342 terawatt-hours (TWh) to 1134 TWh, as illustrated in Figure 2 [2]. It also went up from 1260 TWh in 2018 to 1404 TWh in 2019 [3].

With the accelerating penetration of wind power into the power system, it is difficult for operators to predict the status of the power system. A sudden change in the generating capacity of wind power plants increases the uncertainty factors in operating the power system. Therefore, the power system control center often requires the backup capacity to increase, leading to additional costs for the whole system. While the level of penetration of wind power plants into the power system is still low, its influence on the power system is almost negligible. However, when penetration is high, there are several challenges to address including power imbalances as well as increased system reserves [4]. In order to overcome such problems, it is imperative to build models for wind power prediction with the lowest possible errors. Accurate forecasting of wind power generation can help enhance the stability of the power system, the reliability of power supply, and power quality. Furthermore, the calculation of power balance and economical operation in the power system will be more accurate, thus contributing to reducing its operating costs.

There has been a lot of research on wind power forecasting with different methods, among which statistical methods and artificial neural network (ANN) methods are quite commonly used [5]. For example, models of ANN have been proposed to predict wind power generation capacity, where the ANN is trained to be used in combination with genetic algorithms [6]. Another model was developed using ANN with Gaussian process approximation and adaptive Bayesian learning to predict wind power generation capacity in a short time with intervals such as 5 min, 10 min, 15 min, 20 min, and 30 min [7]. Other researchers have built models utilizing neural networks to predict the wind power generation capacity that can be applied to the power system and electricity market [8]. Various forecasting methods were combined including persistent methods, backpropagation neural networks, and radial basis function (RBF) neural networks to build models for 10-min-ahead wind power prediction [9]. These methods have been prove to facilitate the execution of wind power forecasting.

A number of studies have been found to be related to short-term forecasting models of wind power generation capacity [10]. The researchers, in [11] introduced short-term wind speed forecasting of wind farms based on the least squares support vector machine (SVM) model. Some methods employed by other authors for wind power forecasting include the artificial intelligence network [12] and double-stage hierarchical adaptive neuro-fuzzy inference system (ANFIS) approach [13]. Some have developed forecasting models and applications for the optimal operation of wind farms [14,15]. In [16], the authors provided a comprehensive review of combined approaches for short-term wind speed and wind power forecasting.

Hybrid forecasting methods have also been developed with a combination of weather and historical data in building forecasting models. Adding to these are combined optimization algorithms with current forecasting methods to improve accuracy. Such methods include the double-stage hierarchical hybrid genetic algorithm-ANN (GA-ANN) [17], hybrid intelligent systems [18], double-stage hierarchical hybrid particle swarm optimization-ANN (PSO-ANN) model [19], two-stage hybrid modeling approach based on supervisory, control, and data acquisition system (SCADA), and meteorological information [20,21,22]. Fuzzy methods have also been used by some to build a forecasting model [23,24,25]. In another approach, the Kalman filter was adopted to improve the model of wind speed prediction, thereby reducing errors in wind power generation forecasting [26]. Furthermore, a dual-step integrated machine learning model was introduced based on actual measurement data and environmental factors to improve the accuracy of the forecasting model [27]. Most of the articles above-mentioned have proposed advanced methods and built models of wind power generation forecasting that can be applied to actual production. However, forecasting errors can be further reduced through enhanced optimization methods and machine learning.

In this paper, two new methods of wind power forecasting are proposed: applying the optimization algorithm of PSO and applying GA to a PSO-ANN model. The idea behind these methods is to optimize the parameters of the PSO-ANN model, thus helping reduce the forecasting errors and enhancing prediction accuracy. Initially, a first PSO algorithm is used to adjust the parameters of a neural network in the wind power forecasting model. Then, in the PSO-PSO-ANN method, another particle swarm optimization is used to find the optimal parameters of the first PSO algorithm to improve forecasting accuracy. Similarly, in the GA-PSO-ANN method proposed, the genetic algorithm is used to adjust the parameters of the first PSO algorithm to improve the accuracy of the forecasting results.

The main objectives of this study are listed below:

• Propose a double-optimization approach represented by two new advanced models for wind power forecasting using particle swarm optimization, genetic algorithms, and artificial neural network, the so-called PSO-PSO-ANN and GA-PSO-ANN;
• Develop a wind power forecasting tool based on these models and use data from a real wind power plant to test the tool. Both models are tested with actual data collected from the Tuy Phong wind power plant, which is located in Binh Thuan Province, Vietnam; and
• Increase prediction accuracy in comparison with other forecasting methods. The accuracy indicator of the proposed wind power forecasting models is then compared with that of several known approaches to verify efficiency and advancement.

The rest of this paper is organized as follows. In Section 2, fundamental concepts and structures of the ANN, PSO, GA, and PSO-ANN models are introduced. In Section 3, the two new algorithms GA-PSO-ANN and PSO-PSO-ANN are proposed in detail. These algorithms are used to develop a wind power forecasting tool based on Python, a programming language. As the proposed models are implemented to forecast wind power hourly, Section 4 provides insights into the experimental results and evaluates the accuracy, given some forecasting error benchmarks. Finally, Section 5 contains the discussion and ideas for extending research.

2. Forecasting Methods

2.1. Artificial Neural Network (ANN)

Artificial intelligence is a field that researches and develops ways to make machines capable of reasoning, making judgments, feeling, understanding languages, and solving problems like humans.

The artificial neural network has the same structure as the human brain. However, the difference is that the number of neurons in the ANN depends on the actual needs of the problem, whereas the human brain has approximately 15 billion neurons [28]. An ANN is capable of learning and applying what has been taught, and as a result, it has been strongly developed and employed, especially in the field of forecasting, classification, identification, control, and so on.

In this paper, a feedforward neural network was built to forecast wind power. The general structure of a feedforward multilayer neural network is described as follows [29,30]:

• A multilayer feedforward network consists of an input layer, an output layer, and one or more hidden layers between them.
• Inputs are vectors (x₁, x₂, _,…, x_n) in n-dimensional space, and outputs are vectors (y₁, y₂, …, y_k) in k-dimensional space.
• Each neuron of the current layer is linked with all neurons in the previous layer.
• The output of a previous layer is the input of the next layer.
• The input layer receives data and redistributes them to neurons in the hidden layer(s). The input neurons do not perform any calculations. The information flow in the feedforward neuron network will go from left to right, and the input values (x₁, x₂, x₃, …, x_n) are transmitted to the hidden layer neurons through connection weights, and then taken to the output layer.

In this paper, the neural network structure includes one input layer, one hidden layer, and one output layer, which can be seen in Figure 3 [8]. The weight connected from the ith neuron in the input layer to the hth neuron in the hidden layer is denoted by w¹_ih, and the weight connected from the hth neuron in the hidden layer to the kth neuron in the output layer is denoted by w²_h.

• With the hth neuron in the hidden layer [29,30]:

$${\mathrm{net}}_{\mathrm{h}}={\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{w}}_{\mathrm{ih}}{\mathrm{x}}_{\mathrm{i}}+{\mathrm{b}}_{\mathrm{h}}$$

(1)

$${\mathrm{z}}_{\mathrm{h}}={\mathrm{f}}_1\left({\mathrm{net}}_{\mathrm{h}}\right)$$

(2)

where

• x_i is the ith input variable;
• w_ih is the connection weights between ith input and hth neuron;
• b_h is the bias;
• net_h is the net input or argument of the activation function;
• z_h is the net output; and
• f₁(neth) is the activation function.

The input layer consists of three neurons that represent wind speed, wind direction, and temperature. The output layer has one neuron, which is wind power. The neural network also has ten neurons in the hidden layer. The number of neurons in the hidden layer has been carefully chosen. If this number is too small, it may cause the inability to fully identify the signals in a complex dataset. However, if there are too many, it will increase the time of network training and can lead to overfitting in the forecast. This number depends on factors such as the number of inputs, the output of the network, the number of cases in the sample set, the noise of the target data, the complexity of the error function, the network architecture, and the network training algorithm.

Many trials were made to determine the number of neurons in the hidden layer with different configurations, based on our research experience and the pilot test approach, and simulations were then conducted to perform neural network training and error validation (MAPE). Finally, the number of ten neurons in the hidden layer was chosen because it gave better MAPE values than the remaining trial cases without overfitting.

In this paper, we used tan-sigmoid as the activation function for neurons in the hidden layer and the purelin function for the output layer. Through our research on artificial intelligence and hands-on experience, the tan-sigmoid function is a nonlinear function that can simulate relatively close to the wind turbine’s power curve. Therefore, this function was used as the activation function for the hidden layer. Furthermore, based on the results from many publications, the most appropriate activation function for the output layer of a feedforward neuron network is a linear function. This is the reason why we used purelin, a linear function, to transfer data from the hidden layer to the output layer.

2.2. Particle Swarm Optimization (PSO)

The particle swarm optimization algorithm is one of the algorithms built on the concept of swarm intelligence to find solutions for optimization problems in a certain search space. The algorithm has important applications in many areas, whereby the solving of optimization problems is imperative [31].

The PSO algorithm is a form of the evolutionary algorithms that were previously known such as the genetic algorithm (GA) and ant colony algorithm [32]. However, PSO differs from GA in that it tends to use interactions among individuals in a population to explore the search space. The PSO algorithm is a result of modeling the flight of birds in search of food. It was first introduced in 1995 by James Kennedy and Russell C. Eberhart [31]. It is an optimization tool, in which each particle of the swarm flies in the search space for a potential solution to the problem. The velocity and position of each particle after each iteration can be updated using the current velocity and the distance from its best position (p^best) to swarm best position (g^best) by Equations (3) and (4), as demonstrated in Figure 4 [31,33,34,35]:

• Position of ith particle in the k + 1th iteration:

$${\mathrm{x}}_{\mathrm{k}+1}^{\mathrm{i}}={ \mathrm{x}}_{\mathrm{k}}^{\mathrm{i}}+{\mathrm{v}}_{\mathrm{k}+1}^{\mathrm{i}}$$

(3)

• Velocity of ith particle in the k + 1th iteration:

$${\mathrm{v}}_{\mathrm{k}+1}^{\mathrm{i}}={ \mathrm{wv}}_{\mathrm{k}}^{\mathrm{i}}+{\mathrm{c}}_1{\mathrm{r}}_1\left(p^{best}{}_{\mathrm{k}}^{\mathrm{i}}-{\mathrm{x}}_{\mathrm{k}}^{\mathrm{i}}\right)+{\mathrm{c}}_2{\mathrm{r}}_2\left(g^{best}{}_{\mathrm{k}}^{ }-{\mathrm{x}}_{\mathrm{k}}^{\mathrm{i}}\right)$$

(4)

where

• ${\mathrm{x}}_{\mathrm{k}}^{\mathrm{i}}$ is the position of the particle ith in the kth iteration;
• ${\mathrm{x}}_{\mathrm{k}+1}^{\mathrm{i}}$ is the position of the particle ith in the (k + 1)th iteration;
• ${\mathrm{v}}_{\mathrm{k}}^{\mathrm{i}}$ is the velocity of the ith particle in the kth iteration;
• ${\mathrm{v}}_{\mathrm{k}+1}^{\mathrm{i}}$ is the velocity of the ith particle in the (k + 1)th iteration;
• $p^{best}{}_{\mathrm{k}}^{\mathrm{i}}$ is the best position of the ith particle until the kth iteration;
• $g^{best}{}_{\mathrm{k}}^{ }$ is the best position of the swarm until the kth iteration;
• w is the inertial weight;
• c₁, c₂ are the acceleration coefficients; and
• r₁, r₂ are the random numbers between 0 and 1.

2.3. Generic Algorithm

Genetic algorithm (GA) is a technique of computer science and a subdivision of evolutionary algorithms that seeks the right solution to optimization problems based on the genetic operators: selection, crossover, and mutation [36]. GA is based on two basic biological processes: the genetic theory of Gregor Johan Mendel (1865) and the evolutionary theory of Charles Darwin (1875). It can describe and solve many complex optimization problems in multiple areas such as scheduling problems, sales planning, and traveler’s problems [36,37,38,39]. The flowchart of GA can be seen in Figure 5 [39].

2.4. Particle Swarm Optimization-Artificial Neural Network (PSO-ANN) Hybrid Algorithm

The PSO algorithm is used in training the ANN to determine the set of parameters (w, b), so that the neural network can be best built and fit with the data [40]. The concept of the PSO-ANN algorithm is shown in Figure 6, with the PSO being used to train the ANN.

The number of parameters of ANN is determined by:

N = n × h + m × h + h + m = 3 × h + 1 × h + h + 1 = 5h + 1

(5)

where

• N is the number of parameters of the neural network;
• n is the number of neurons in the input layer;
• h is the number of neurons in the hidden layer; and
• m is the number of neurons in the output layer.

The size of the search space is defined based on the neural network structure:

D = N = 5 h + 1 = 5 × 10 + 1 = 51

(6)

Through experiments, several sets of PSO parameters were considered. Then, these sets were tested using the trial-and-error approach to select the set of parameters that produced the best result (smallest MAPE). The best set of PSO parameters with the relevant values are described in

Table 1. Values of the particle swarm optimization (PSO) parameters.

Parameter	Description	Value
w	inertial weight	0.72
c1	particle coefficient	1
c2	swarm coefficient	1.5
iteration_max	maximum iteration	2000
r1, r2	random numbers	[0;1]
n_particles	number of particles	100
D	search space dimension	51

.

The procedure to implement the PSO-ANN hybrid algorithm is described below:

• Step 1: Read and separate historical data into a training set (for training the neural network) and a test set (for testing the neural network).
• Step 2: Specify PSO parameters.
• Step 3: Generate an initial swarm with random position and velocity values for all particles. Each particle is a unique neural network. Hence, the number of neural networks is equal to the size of the swarm (or the number of particles in the swarm).
• Step 4: Train the initial neural networks and calculate the fitness function value (mean absolute percent error, MAPE) for each particle. Then, calculate f_i^best, f_g^best.
• Step 5: Update the velocity and position of each particle.
• Step 6: For each particle, train the current neural networks, and recalculate the fitness function value. If the current fitness function value is better than its best fitness function value in the previous iteration, then the f_i^best will be updated to the current fitness function value, and the particle best position (p_best) will be updated to the current position of the particle. After that, if the fⁱ_best value is better than f^g_best, then the swarm best fitness function value f^g_best will be updated by the current fⁱ_best value, and swarm best position (g_best) is updated to the best particle position.
• Step 7: If the maximum iteration is reached, then proceed to step 8. Otherwise, go back to step 5.
• Step 8: Check if the error is less than the pre-defined error epsilon ($ℰ$). If yes, print the optimized neural network parameters. Otherwise, we start the whole process again.

The whole process can be illustrated in Figure 7.

3. Proposing Algorithms for Short-Term Wind Power Forecasting

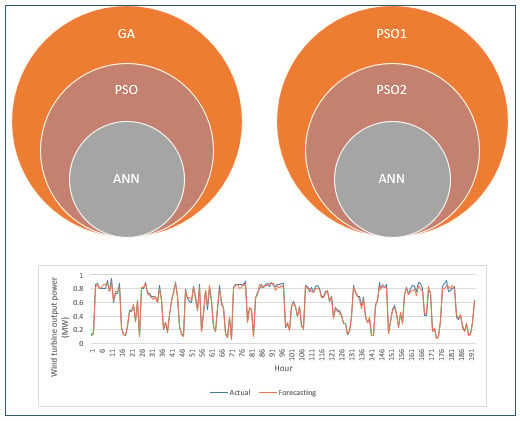
3.1. Proposing Particle Swarm Optimization – Particle Swarm Optimization – Artificial Neural Network (PSO-PSO-ANN) Hybrid Algorithm

In order to improve the accuracy of the wind power forecasting, this paper proposed a PSO-PSO-ANN algorithm, whose structure consists of three main rings: PSO1 loop, PSO2 loop, and neural network loop (Figure 8). In this structure, the outer loop PSO1 uses the PSO algorithm to determine the best values of parameters c₁, c₂, and w of the PSO2 loop. Similarly, the PSO2 loop uses the PSO algorithm to adjust the parameters of the neural network, as described in Section 2.4.

The procedure for implementing the PSO-PSO-ANN hybrid algorithm is now presented in Figure 9, where

• ${\mathrm{x}}_{1\mathrm{i}}^{\mathrm{init}}$ is the initial position of the ith particle of the PSO1 algorithm;
• ${\mathrm{x}}_{2\mathrm{i}}^{\mathrm{init}}$ is the initial position of the ith particle of the PSO2 algorithm;
• ${\mathrm{v}}_{1\mathrm{i}}^{\mathrm{init}}$ is the initial velocity of the ith particle of the PSO1 algorithm;
• ${\mathrm{v}}_{2\mathrm{i}}^{\mathrm{init}}$ is the initial velocity of the ith particle of the PSO2 algorithm;
• ${\mathrm{p}}_{1\mathrm{i}}^{\mathrm{best}}$ is the best position of the ith particle of the PSO1 algorithm;
• ${\mathrm{p}}_{2\mathrm{i}}^{\mathrm{best}}$ is the best position of the ith particle of the PSO2 algorithm;
• ${\mathrm{f}}_{1\mathrm{i}}^{\mathrm{current}}$ is the fitness function value of the ith particle in the current iteration of the PSO1 algorithm;
• ${\mathrm{f}}_{2\mathrm{i}}^{\mathrm{current}}$ is the fitness function value of the ith particle in the current iteration of the PSO2 algorithm;
• ${\mathrm{f}}_{1\mathrm{i}}^{\mathrm{best}}$ is the best fitness function value of the ith particle of the PSO1 algorithm;
• ${\mathrm{f}}_{2\mathrm{i}}^{\mathrm{best}}$ is the best fitness function value of the ith particle of the PSO2 algorithm;
• ${\mathrm{g}}_1^{\mathrm{best}}$ is the best position of the PSO1 algorithm;
• ${\mathrm{g}}_2^{\mathrm{best}}$ is the best position of the PSO2 algorithm;
• ${\mathrm{f}}_1^{\mathrm{best}}$ is the best fitness function value of the PSO1 algorithm;
• ${\mathrm{f}}_2^{\mathrm{best}}$ is the best fitness function value of the PSO2 algorithm;
• iteration1, iteration2 are the current iterations of the PSO1 and PSO2 loop; and
• iteration_max1, iteration_max2 are the maximum iterations of the PSO1 and PSO2 loop.

3.2. Proposing GA-PSO-ANN Hybrid Algorithm

Aside from PSO-PSO-ANN, the GA-PSO-ANN algorithm is also used to improve the accuracy of wind power forecasting. Its structure consists of three main rings: the GA loop, PSO loop, and the neural network loop (see Figure 10). In this structure, the outer loop GA uses a genetic algorithm to determine the best values of the parameters c₁, c₂, and w of the PSO loop. Similarly, the PSO loop uses the PSO algorithm to adjust the parameters of the neural network, as described in Section 2.4.

The procedure to implement the GA-PSO-ANN hybrid algorithm is demonstrated in Figure 11, where

• ${\mathrm{x}}_{\mathrm{i}}^{\mathrm{init}}$ is the initial position of the ith particle of the PSO algorithm;
• ${\mathrm{v}}_{\mathrm{i}}^{\mathrm{init}}$ is the initial velocity of the ith particle of the PSO algorithm;
• ${\mathrm{p}}_{\mathrm{i}}^{\mathrm{best}}$ is the best position of the ith particle of the PSO algorithm;
• ${\mathrm{f}}_{\mathrm{i}}^{\mathrm{current}}$ is the fitness function value of the ith particle in the current iteration of the PSO algorithm;
• ${\mathrm{f}}_{\mathrm{i}}^{\mathrm{best}}$ is the best fitness function value of the ith particle of the PSO algorithm;
• ${\mathrm{g}}_{}^{\mathrm{best}}$ is the best position of the PSO algorithm;
• ${\mathrm{f}}_{}^{\mathrm{best}}$ is the best fitness function value of the PSO algorithm; and
• Q is the population that consists of solutions (Q₁, Q₂, …, Q_N), Q_i = (c_1i, c_2i, w_i) with i = 1, 2, 3, …, N. N is the number of solutions of the population.

3.3. Data

The historical data including wind turbine output power, wind speed, wind direction, and temperature were used to train the models, as shown in Figure 12. These data were collected periodically with a 30-min cycle, taken from Tuy Phong wind farm, located in Binh Thuan Province, Vietnam. The entire dataset consists of 3866 records [8].

The 3866 data records were divided into two sets (i.e., training set and test set). The former had 3479 records, which were used to train the neural network, while the latter had 387 records used to check the accuracy of the model.

3.4. Programing Language

Based on the proposed GA-PSO-ANN and PSO-PSO-ANN algorithms, the wind power forecasting tool was built using Python, a high-level and object-oriented programming language. Python has a clear structure that is easy to understand and easy to use. Additionally, codes written in Python are often found to be shorter than other programming languages. In particular, Python supports a lot of math libraries, machine learning, data science, and optimization algorithm libraries [41].

4. Results

4.1. Evaluation Method

The mean absolute percentage error (MAPE) and mean square error (MSE) indices were used to evaluate the effectiveness of the proposed wind power forecasting models [42].

Mean absolute percentage error is calculated using the following equation [8,43,44]:

$$\mathrm{MAPE} =\frac{1}{\mathrm{N}}{\displaystyle \sum }_{\mathrm{i} =1}^{\mathrm{N}}\frac{\left|{\mathrm{P}}_{\mathrm{i}}^{\mathrm{true}}-{\mathrm{P}}_{\mathrm{i}}^{\mathrm{predict}}\right|}{{\mathrm{P}}_{\mathrm{i}}^{\mathrm{true}}}100\%$$

(7)

Mean square error [43,44] is determined by:

$$\mathrm{MSE} =\frac{1}{\mathrm{N}}{\displaystyle \sum }_{\mathrm{i} =1}^{\mathrm{N}}{\left({\mathrm{P}}_{\mathrm{i}}^{\mathrm{true}}-{\mathrm{P}}_{\mathrm{i}}^{\mathrm{predict}}\right)}^2$$

(8)

where

• ${\mathrm{P}}_{\mathrm{i}}^{\mathrm{true}}$ is the ith actual power value;
• ${\mathrm{P}}_{\mathrm{i}}^{\mathrm{predict}}$ is the ith forecasted power value; and
• N is the total number of records of the data.

4.2. Experimental Results

For more accuracy evaluation, each proposed algorithm was used to train and test the neural network 24 times to calculate the average MSE and MAPE. The results compared with the PSO-ANN and Adam-ANN methods [45,46] are shown in

Table 2. Error results of the proposed methods compared with the Particle Swarm Optimization – Artificial Neural Network and Adam-Artificial Neural Network.

Testing Time	GA-PSO-ANN		PSO-PSO-ANN		PSO-ANN		Adam-ANN
	MSE	MAPE	MSE	MAPE	MSE	MAPE	MSE	MAPE
1	0.0011	4.53%	0.0011	4.58%	0.0011	4.72%	0.00057	6.20%
2	0.0011	4.50%	0.0011	4.51%	0.0011	4.65%	0.00060	6.46%
3	0.0012	4.53%	0.0011	4.56%	0.0013	5.16%	0.00054	8.30%
4	0.001	4.43%	0.0013	4.59%	0.0012	5.05%	0.00053	6.94%
5	0.0011	4.52%	0.0011	4.54%	0.0012	4.93%	0.00058	5.80%
6	0.0013	4.54%	0.0011	4.47%	0.0011	4.65%	0.00053	7.00%
7	0.0013	4.65%	0.0011	4.58%	0.0012	4.84%	0.00054	6.07%
8	0.0011	4.55%	0.0011	4.50%	0.0011	4.56%	0.00059	6.70%
9	0.0011	4.53%	0.0011	4.55%	0.0014	4.77%	0.00060	6.85%
10	0.0012	4.52%	0.0011	4.42%	0.0012	5.03%	0.00057	6.79%
11	0.0011	4.44%	0.0011	4.59%	0.0013	5.37%	0.00051	5.92%
12	0.0011	4.48%	0.0011	4.60%	0.0011	4.76%	0.00060	6.59%
13	0.0012	4.56%	0.0011	4.54%	0.0012	4.89%	0.00055	6.93%
14	0.0011	4.44%	0.0011	4.54%	0.0011	4.58%	0.00054	5.52%
15	0.0011	4.51%	0.0011	4.49%	0.0012	5.00%	0.00055	6.51%
16	0.0011	4.46%	0.0011	4.53%	0.0013	5.17%	0.00060	6.40%
17	0.0011	4.54%	0.0011	4.52%	0.0013	5.36%	0.00057	6.14%
18	0.0011	4.53%	0.0011	4.46%	0.0012	4.82%	0.00054	5.52%
19	0.0011	4.55%	0.0011	4.62%	0.0012	4.94%	0.00056	7.20%
20	0.0013	4.55%	0.0013	4.58%	0.0012	4.89%	0.00053	6.55%
21	0.0012	4.57%	0.0011	4.54%	0.0013	5.12%	0.00054	6.27%
22	0.0012	4.62%	0.0011	4.53%	0.0012	4.93%	0.00055	6.33%
23	0.0011	4.53%	0.0011	4.60%	0.0012	4.73%	0.00054	6.40%
24	0.0011	4.48%	0.0011	4.58%	0.0012	4.79%	0.00056	6.09%
Average	0.0011	4.52%	0.0011	4.54%	0.0012	4.90%	0.00056	6.48%

.

Figure 13 and Figure 14 show the MAPE and MSE indices for 24 testing times of all four models (built on the four aforementioned methods). In the figures, the PSO-PSO-ANN and GA-PSO-ANN models had more stable accuracy than the PSO-ANN and Adam-ANN models.

The average results of the MSE and MAPE are now shown in

Table 3. Average results of the MSE and MAPE.

Algorithm	MAPE	MSE
GA-PSO-ANN	4.52%	0.001139635
PSO-PSO-ANN	4.54%	0.001117418
PSO-ANN	4.90%	0.001212124
Adam-ANN	7.79%	0.001235203

and Figure 15 and Figure 16.

The average result of MAPE across the 24 testing times for the GA-PSO-ANN algorithm was 4.52%, PSO-PSO-ANN was 4.54%, PSO-ANN was 4.90%, and Adam-ANN was 7.79%. Both PSO-PSO-ANN and GA-PSO-ANN algorithms provided better results than the PSO-ANN and Adam-ANN. Out of the four, the GA-PSO-ANN algorithm had the best result, which was slightly better than the PSO-PSO-ANN algorithm.

The average results of MSE in the 24 testing times for the GA-PSO-ANN, PSO-PSO-ANN, PSO-ANN, and Adam-ANN algorithms were 0.00114, 0.00112, 0.00121, and 0.00123, respectively. In the case of the MSE index, PSO-PSO-ANN had the best result among these four algorithms. Again, the two algorithms PSO-PSO-ANN and GA-PSO-ANN can be seen to provide better results than PSO-ANN and Adam-ANN.

In both cases, the proposed algorithms GA-PSO-ANN and PSO-PSO-ANN have outstanding results compared with PSO-ANN and Adam-ANN. Since the forecasting-versus-actual-result graphs for the two proposed algorithms resembled each other, graphs for the GA-PSO-ANN are shown as follows to represent both. As illustrated in Figure 17 and Figure 18, the wind power forecasting results for one day (Figure 17) and for one week (Figure 18) by the proposed GA-PSO-ANN models were quite similar to the actual wind power archived via the SCADA system.

5. Discussion

This paper demonstrated a tool that was built for the forecasting of wind power generation output with a high level of accuracy. By means of an open-source Python programming language, a wind power forecasting program was built with a hybrid application of an artificial neural network, particle swarm optimization algorithm, and genetic algorithm. Specifically, the particle swarm optimization algorithm was used to train the artificial neural networks (PSO-ANN model). In order to reduce errors and improve accuracy in forecasting, the authors used another particle swarm optimization algorithm and genetic algorithm (PSO-PSO-ANN and GA-PSO-ANN models) for the optimal adjustment of the first PSO parameters during neural network training. The two models were successfully applied for the forecasting power output of the Tuy Phong wind power plant in Binh Thuan Province, Vietnam. The results show that the forecasting models PSO-PSO-ANN and GA-PSO-ANN provided better results than the PSO-ANN or Adam-ANN models.

Table 4. Comparison of Mean Absolute Percentage Error (MAPE) among different wind power forecasting models.

Algorithm	MAPE
GA-PSO-ANN	4.52%
PSO-PSO-ANN	4.54%
PSO-ANN	4.90%
Adam-ANN	7.79%
Persistence	11.94%
BP-FFANN	7.35%
GA-FFANN	6.79%
ANFIS	14.92%
WT + ANFIS	12.58%
WT + NNPSO	8.19%
WT-ACO-FFANN	5.35%
VWPF	6.85%

shows the comparison of MAPE between the different wind power forecasting models [8,27,47]. The proposed models PSO-PSO-ANN and GA-PSO-ANN showed better accuracy than the aforementioned models, which indicates that the proposed models in this model can be well used for forecasting in the actual production of wind farms while ensuring a higher level of accuracy.

Wind power generation forecasting plays an important role in optimizing the operation of the power system and electricity market. The models proposed can be expanded and further developed to improve the accuracy of the forecasting results. With the mismatch in forecasting wind power in several wind farms being minimized, the reservation capacity in the power system is very likely to reduce, thus increasing the efficiency of the operation in the electricity market. Some extensions to this piece of research can be considered, ranging from a study on an algorithm to filter and eliminate noise in the input data to an investigation into the algorithm to determine the optimal number of hidden layers in neural networks to give predictive results with the lowest error, to name just a few.