Management and Performance Control Analysis of Hybrid Photovoltaic Energy Storage System under Variable Solar Irradiation
Abstract
:1. Introduction
1.1. Background
1.2. Literature Review
1.3. Contributions
- Optimization of the power generated by photovoltaic system,
- Balancing the voltage of the DC voltage to the appropriate value,
- Control and management of the currents to their corresponding values in the supercapacitor and battery,
- Reduce the stress in the battery by using the supercapacitor,
- Protect the system from charge/discharge or surcharge and maintain it to the global stabilization,
- Regulate the transfer of the energy between the hybrid system and DC-link.
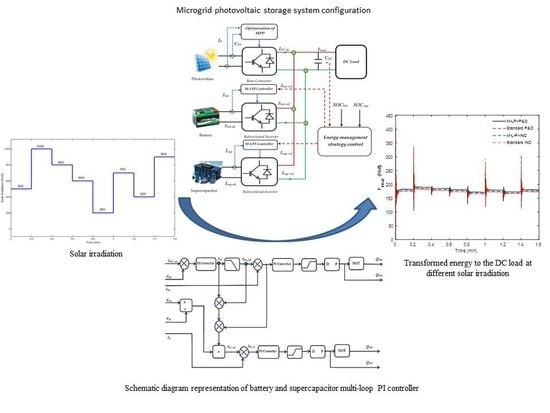
2. Hybrid Energy Storage System Configuration and Modelling
2.1. Photovoltaic Modelling
2.2. Lithium–Ion Battery Modelling
2.3. Supercapacitor Modelling
3. Operation Point Optimization
3.1. Perturb and Observe (P&O) Formulation
3.2. Incremental Conductance (INC) Formulation
3.3. Control and Management of Storage System
- Balancing the voltage of the DC link voltage to the appropriate value,
- Controlling the battery and supercapacitor currents to their corresponding values,
- Maintaining global system stabilization.
4. Simulation Results and Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Subramani, G.; Vigna, K.R.; Sanjeevikumar, P.; Jens, B.H.; Frede, B.; Leonowicz, Z.; Pawel, K. Techno-Economic Optimization of Grid-Connected Photovoltaic (PV) and Battery Systems Based on Maximum Demand Reduction (MDRed) Modelling in Malaysia. Energies 2019, 12, 3531. [Google Scholar] [CrossRef] [Green Version]
- Louzazni, M.; Khouya, A.; Amechnoue, K.; Gandelli, A.; Mussetta, M.; Crăciunescu, A. Metaheuristic Algorithm for Photovoltaic Parameters: Comparative Study and Prediction with a Firefly Algorithm. Appl. Sci. 2018, 8, 339. [Google Scholar] [CrossRef] [Green Version]
- Vyas, M.; Jain, M.; Pareek, K.; Garg, A. Multivariate optimization for maximum capacity of lead acid battery through Taguchi method. Measurement 2019, 148, 106904. [Google Scholar] [CrossRef]
- Jing, W.; Lai, C.H.; Wong, W.S.H.; Wong, M.L.D. A comprehensive study of battery-supercapacitor hybrid energy storage system for standalone PV power system in rural electrification. Appl. Energy 2018, 224, 340–356. [Google Scholar] [CrossRef]
- Jiang, L.L.; Srivatsan, R.; Maskell, D.L. Computational intelligence techniques for maximum power point tracking in PV systems: A review. Renew. Sustain. Energy Rev. 2018, 85, 14–45. [Google Scholar] [CrossRef]
- Mukerjee, A.K.; Dasgupta, N. DC power supply used as photovoltaic simulator for testing MPPT algorithms. Renew. Energy 2007, 32, 587–592. [Google Scholar] [CrossRef]
- Chantana, J.; Kawano, Y.; Kamei, A.; Minemoto, T. Description of degradation of output performance for photovoltaic modules by multiple regression analysis based on environmental factors. Optik (Stuttg) 2019, 179, 1063–1070. [Google Scholar] [CrossRef]
- Louzazni, M.; Khouya, A.; Al-Dahidi, S.; Mussetta, M.; Amechnoue, K. Analytical Optimization of Photovoltaic Output with Lagrange Multiplier Method. Optik (Stuttg) 2019, 199, 163379. [Google Scholar] [CrossRef]
- Nguyen, B.N.; Nguyen, V.T.; Duong, M.Q.; Le, K.H.; Nguyen, H.H.; Doan, A.T. Propose a MPPT Algorithm Based on Thevenin Equivalent Circuit for Improving Photovoltaic System Operation. Front. Energy Res. 2020, 8, 14. [Google Scholar] [CrossRef] [Green Version]
- Kumar, G.; Trivedi, M.B.; Panchal, A.K. Innovative and precise MPP estimation using P–V curve geometry for photovoltaics. Appl. Energy 2015, 138, 640–647. [Google Scholar] [CrossRef]
- Balato, M.; Petrarca, C. The Impact of Reconfiguration on the Energy Performance of the Distributed Maximum Power Point Tracking Approach in PV Plants. Energies 2020, 13, 1511. [Google Scholar] [CrossRef] [Green Version]
- Al-Gizi, A.; Al-Chlaihawi, S.; Louzazni, M.; Craciunescu, A. Genetically optimization of an asymmetrical fuzzy logic based photovoltaic maximum power point tracking controller. Adv. Electr. Comput. Eng. 2017, 17, 69–76. [Google Scholar] [CrossRef]
- Lazaroiu, G.C.; Longo, M.; Roscia, M.; Pagano, M. Comparative analysis of fixed and sun tracking low power PV systems considering energy consumption. Energy Convers. Manag. 2015, 92, 143–148. [Google Scholar] [CrossRef]
- Tchakounté, H.; Fapi, C.B.N.; Kamta, M.; Djalo, H.; Woafo, P. Experimental Assessment of a Smart Sun Tracking System Consumption for the Improvement of a Crystalline Silicon Photovoltaic Module Performance under Variable Weather Conditions. Appl. Sol. Energy 2019, 55, 385–396. [Google Scholar] [CrossRef]
- Sahin, F.E. Fisheye lens design for sun tracking cameras and photovoltaic energy systems. J. Photonics Energy 2018, 8. [Google Scholar] [CrossRef]
- Sahin, F.E.; Yılmaz, M. High Concentration Photovoltaics (HCPV) with Diffractive Secondary Optical Elements. Photonics 2019, 6, 68. [Google Scholar] [CrossRef] [Green Version]
- Ju, X.; Xu, C.; Hu, Y.; Han, X.; Wei, G.; Du, X. A review on the development of photovoltaic/concentrated solar power (PV-CSP) hybrid systems. Sol. Energy Mater. Sol. Cells 2017, 161, 305–327. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. A Maximum Power Point Tracking (MPPT) for PV system using Cuckoo Search with partial shading capability. Appl. Energy 2014, 119, 118–130. [Google Scholar] [CrossRef]
- Chao, K.-H.; Lin, Y.-S.; Lai, U.-D. Improved particle swarm optimization for maximum power point tracking in photovoltaic module arrays. Appl. Energy 2015, 158, 609–618. [Google Scholar] [CrossRef]
- Mutarraf, M.U.; Terriche, Y.; Niazi, K.A.K.; Khan, F.; Vasquez, J.C.; Guerrero, J.M. Control of Hybrid Diesel/PV/Battery/Ultra-Capacitor Systems for Future Shipboard Microgrids. Energies 2019, 12, 3460. [Google Scholar] [CrossRef] [Green Version]
- Tofighi, A.; Kalantar, M. Power management of PV/battery hybrid power source via passivity-based control. Renew. Energy 2011, 36, 2440–2450. [Google Scholar] [CrossRef]
- Luta, D.N.; Raji, A.K. Optimal sizing of hybrid fuel cell-supercapacitor storage system for off-grid renewable applications. Energy 2019, 166, 530–540. [Google Scholar] [CrossRef]
- Cabrane, Z.; Ouassaid, M.; Maaroufi, M. Analysis and evaluation of battery-supercapacitor hybrid energy storage system for photovoltaic installation. Int. J. Hydrogen Energy 2016, 41, 20897–20907. [Google Scholar] [CrossRef]
- Nassef, A.M.; Fathy, A.; Rezk, H. An Effective Energy Management Strategy Based on Mine-Blast Optimization Technique Applied to Hybrid PEMFC/Supercapacitor/Batteries System. Energies 2019, 12, 3796. [Google Scholar] [CrossRef] [Green Version]
- Mendis, N.; Muttaqi, K.M.; Perera, S. Management of low- and high-frequency power components in demand-generation fluctuations of a DFIG-based wind-dominated RAPS system using hybrid energy storage. IEEE Trans. Ind. Appl. 2014, 50, 2258–2268. [Google Scholar] [CrossRef]
- Bambang, R.T.; Rohman, A.S.; Dronkers, C.J.; Ortega, R.; Sasongko, A. Energy management of fuel cell/battery/supercapacitor hybrid power sources using model predictive control. IEEE Trans. Ind. Inform. 2014, 10, 1992–2002. [Google Scholar] [CrossRef]
- Tey, K.S.; Mekhilef, S. Modified incremental conductance MPPT algorithm to mitigate inaccurate responses under fast-changing solar irradiation level. Sol. Energy 2014, 101, 333–342. [Google Scholar] [CrossRef]
- Li, C.; Chen, Y.; Zhou, D.; Liu, J.; Zeng, J. A High-Performance Adaptive Incremental Conductance MPPT Algorithm for Photovoltaic Systems. Energies 2016, 9, 288. [Google Scholar] [CrossRef] [Green Version]
- “Waaree Energies | WS-250 to WS-275 | Fiche Technique Panneau Solaire | Annuaire Panneau ENF”. Available online: https://fr.enfsolar.com/pv/panel-datasheet/crystalline/25814 (accessed on 17 April 2020).
- Louzazni, M.; Khouya, A.; Amechnoue, K.; Mussetta, M.; Crăciunescu, A. Comparison and evaluation of statistical criteria in the solar cell and photovoltaic module parameters’ extraction. Int. J. Ambient Energy 2018, 17, 1–13. [Google Scholar] [CrossRef]
- Cotfas, D.T.; Deaconu, A.M.; Cotfas, P.A. Application of successive discretization algorithm for determining photovoltaic cells parameters. Energy Convers. Manag. 2019, 196, 545–556. [Google Scholar] [CrossRef]
- Louzazni, M.; Craciunescu, A.; Dumitrache, A. Identification of Solar Cell Parameters with Firefly Algorithm. In Proceedings of the 2nd International Conference on Mathematics and Computers in Sciences and in Industry, Sliema, Malta, 3 March 2016. [Google Scholar] [CrossRef]
- Louzazni, M. An analytical mathematical modeling to extract the parameters of solar cell from implicit equation to explicit form. Appl. Sol. Energy 2015, 51, 165–171. [Google Scholar] [CrossRef]
- Rezaei, M.M.; Asadi, H. A Modified perturb-and-observe-based Maximum Power Point Tracking Technique for Photovoltaic Energy Conversion Systems. J. Control Autom. Electr. Syst. 2019, 30, 822–831. [Google Scholar] [CrossRef]
- Li, C.H.; Zhu, X.J.; Cao, G.Y.; Hu, W.Q.; Sui, S.; Hu, M.R. A maximum power point tracker for photovoltaic energy systems based on fuzzy neural networks. J. Zhejiang Univ. Sci. A 2009, 10, 263–270. [Google Scholar] [CrossRef]
- Wei, Z.; Leng, F.; He, Z.; Zhang, W.; Li, K. Online State of Charge and State of Health Estimation for a Lithium-Ion Battery Based on a Data–Model Fusion Method. Energies 2018, 11, 1810. [Google Scholar] [CrossRef] [Green Version]
- Meng, J.; Boukhnifer, M.; Diallo, D.; Wang, T. A New Cascaded Framework for Lithium-Ion Battery State and Parameter Estimation. Appl. Sci. 2020, 10, 1009. [Google Scholar] [CrossRef] [Green Version]
- Lin, X. Theoretical Analysis of Battery SOC Estimation Errors under Sensor Bias and Variance. IEEE Trans. Ind. Electron. 2018, 65, 7138–7148. [Google Scholar] [CrossRef]
- Chen, Z.; Fu, Y.; Mi, C.C. State of charge estimation of lithium-ion batteries in electric drive vehicles using extended Kalman filtering. IEEE Trans. Veh. Technol. 2013, 62, 1020–1030. [Google Scholar] [CrossRef]
- Gualous, H.; Bouquain, D.; Berthon, A.; Kauffmann, J.M. Experimental study of supercapacitor serial resistance and capacitance variations with temperature. J. Power Sources 2003, 123, 86–93. [Google Scholar] [CrossRef]
- Tiwari, G.N.; Dubey, S. Fundamentals of Photovoltaic Modules and Their Applications; Royal Society of Chemistry: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Al-Gizi, A.; Louzazni, M.; Fadel, M.A.; Craciunescu, A. Critical constant illumination time in comparison of two photovoltaic maximum power point tracking algorithms. UPB Sci. Bull. Ser. C Electr. Eng. Comput. Sci. 2018, 80, 201–216. [Google Scholar]
- Liu, F.; Duan, S.; Liu, F.; Liu, B.; Kang, Y. A variable step size INC MPPT method for PV systems. IEEE Trans. Ind. Electron. 2008, 55, 2622–2628. [Google Scholar] [CrossRef] [Green Version]

















| Old Perturbation Voltage | Slope of Power | New Perturbation |
|---|---|---|
| Positive | Positive | Positive |
| Positive | Negative | Negative |
| Negative | Positive | Negative |
| Negative | Negative | Positive |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Louzazni, M.; Cotfas, D.T.; Cotfas, P.A. Management and Performance Control Analysis of Hybrid Photovoltaic Energy Storage System under Variable Solar Irradiation. Energies 2020, 13, 3043. https://doi.org/10.3390/en13123043
Louzazni M, Cotfas DT, Cotfas PA. Management and Performance Control Analysis of Hybrid Photovoltaic Energy Storage System under Variable Solar Irradiation. Energies. 2020; 13(12):3043. https://doi.org/10.3390/en13123043
Chicago/Turabian StyleLouzazni, Mohamed, Daniel Tudor Cotfas, and Petru Adrian Cotfas. 2020. "Management and Performance Control Analysis of Hybrid Photovoltaic Energy Storage System under Variable Solar Irradiation" Energies 13, no. 12: 3043. https://doi.org/10.3390/en13123043
APA StyleLouzazni, M., Cotfas, D. T., & Cotfas, P. A. (2020). Management and Performance Control Analysis of Hybrid Photovoltaic Energy Storage System under Variable Solar Irradiation. Energies, 13(12), 3043. https://doi.org/10.3390/en13123043