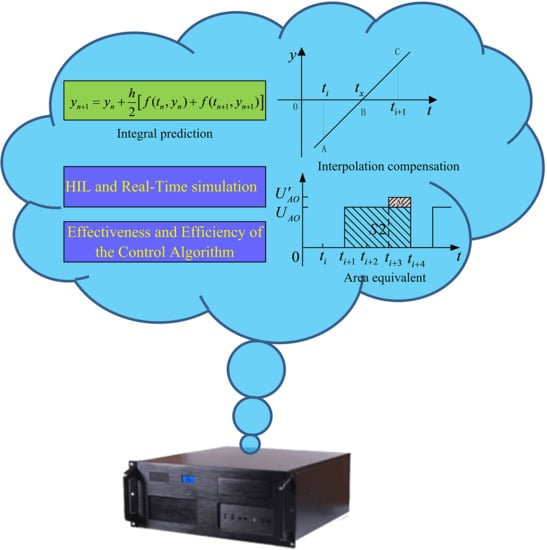
A Study of Interpolation Compensation Based Large Step Simulation of PWM Converters
Abstract
:1. Introduction
- (1)
- dSPACE [20]: The dSPACE real-time simulation system is a development and testing platform of a control system developed by the German company dSPACE, which can seamlessly access MATLAB/Simulink. The software system and hardware cards adopted in this simulation platform are independently developed by dSPACE with a high computational capacity and processing speed. Besides, various I/O boards are offered so that users can make combinations based on their demands for semi-physical simulation in various fields. dSPACE is highly reliable and real-time, but relatively expensive due to the exclusive systems and hardware platforms.
- (2)
- RT-LAB [21]: RT-LAB is a real-time simulation platform developed by the Canadian company OPAL-RT. It can also seamlessly access MATLAB/Simulink. For real-time simulation of power electronics systems, the Artemis real-time solution algorithm and RT-EVENTS are developed. By in-event interpolation compensation, the fixed-step real-time simulation of a power electronics system is realized. The main features of RT-LAB real-time simulation system include openness, expandability and compatibility with PC microprocessors and standard I/O cards. As a result, the hardware cost is reduced, and practicability is enhanced. However, RT-LAB toolboxes are data encrypted. Users have to pay a high price for use.
- (3)
- PSCAD [22]: All switches and trigger modules in the electromagnetic transients including DC (EMTDC) toolbox of power systems computer aided design (PSCAD) support interpolation. By identifying and using the interpolation time based on input information, this function changes the state of switches and the parameters of other modules, such as voltage and current. However, most real-time simulators are based on the RTW of MATLAB/Simulink and poorly compatible with PSCAD. To replace the background program temporarily will result in unnecessary time and cost.
- (1)
- An integral prediction algorithm based on the implicit trapezoid method can accurately predict the value of the modulation wave of the next step and solve the switch delay in a fixed-step real-time simulation by a linear interpolation algorithm. Relying on the algorithm, the moment when the switch acts between the sampling points of simulation steps can be accurately determined to offer favorable conditions for the correction of output voltage from the converter.
- (2)
- In this paper, a S-function-based PWM generator modeling and Simulink-function-based insulated gate bipolar transistor (IGBT) modeling are proposed. The PWM generator mathematical model can output not only normal PWM signals but also time variables of pulse indication signals and switch action, while an IGBT mathematical model can correct the output signals if and when necessary.
- (3)
- In this paper, a control algorithm for the output voltage correction of converter based on the area equivalent principle is proposed. The algorithm ensures the correctness and accuracy of the output voltage and current of converter via the accurate equivalent pulse from IGBT in each switching cycle.
2. Interpolation Prediction Algorithm
2.1. Integral Prediction
2.2. Interpolation Algorithm
2.3. Solution of Multiple Switching
3. Converter Modeling
3.1. PWM Generator Modeling
- (1)
- Fixed-step sampling point ti: sampling the logic relationship between the modulation wave and the carrier wave is known as false (ur < uc) at the current step and true (ur > uc) at the next step. Therefore, the modulation wave and the carrier wave are expected to intersect in a step from ti to ti+1, and the PWM signal at the intersection changes from low level to high level. Therefore, at the present moment, PWM’, the pulse indication signal, is changed from low level to high level, and the time corresponding to tx is recorded as tx(i).
- (2)
- Fixed-step sampling point ti+1: the logic relationship between ti+1 and ti+2 is judged as XNOR by the method used in (1). Accordingly, the pulse indication signal remains at the high level as before. As the modulation wave intersects with the carrier wave in the previous step (between ti and ti+1), the PWM signal changes from low level to high level here.
- (3)
- Fixed-step sampling point ti+2: the logic relationship between ti+2 and ti+3 is judged as XNOR. Accordingly, the pulse indication signal remains at the high level as before while the PWM signal does not change.
- (4)
- Fixed-step sampling point ti+3: the logic relationship between ti+2 and ti+3 is judged as XOR. Accordingly, the pulse indication signal changes from high level to low level, and the time when the carrier wave intersects with the modulation wave is calculated and recorded as tx(i+3). The PWM signal remains unchanged.
- (5)
- Fixed-step sampling point ti+4: the logic relationship between ti+3 and ti+4 is judged as XOR. Accordingly, the pulse indication signal PWM’ changes from low level to high level again, and the time corresponding to tx is recorded. As the modulation wave intersects with the carrier wave in the previous step (between ti+3 and ti+4), the PWM signal changes from high level to low level.
- (a)
- If at the present and the next-step sampling points, the logic relationship between the modulation wave and the carrier wave is XOR, the logic level of the pulse width indication signal shall change, and the time when they intersect shall be recorded. Otherwise, neither the logic level of the pulse width indication signal shall be changed, nor shall the time of intersection be recorded.
- (b)
- If the carrier wave intersects with the modulation wave between the present and the previous-step sampling points, the logic level of the PWM signals shall change; otherwise, it remains the same.
- (c)
- The pulse indication signal PWM’ is as wide as the PWM, but acts at 1 step in advance, creating conditions for correcting IGBT output voltage later.
- (d)
- The tx at the rising/falling edge of the pulse indication signal PWM’ is recorded as the initial/final value, and their difference is expressed as .
- (e)
- As the PWM signal changes only at the fixed-step sampling point, a delay is expected as compared to the actual time when the modulation wave and the carrier wave intersect. The time difference ∆t calculated based on the pulse indication signal PWM’ accurately represent the pulse width of the PWM signal in a switching cycle.
3.2. IGBT Mathematical Modeling
3.3. Calculation of Phase Voltage
3.4. Calculation of DC Bus Current
4. Correction Compensation Algorithm
5. Case Analysis
5.1. Interpolation Algorithm-Based Case Analysis of Converter
5.2. Analysis of PWM Effectiveness Based on Interpolation Prediction Model
5.3. Efficient Analysis Based on Interpolation Prediction Model
5.4. Real-Time Simulation Based on Interpolation Prediction Model
6. Conclusions
- (1)
- In the interpolation-prediction-based PWM generator modeling method, the switching point at any moment under the fixed-step simulation condition can be determined by one-time integral prediction and linear interpolation. The accuracy of the switching point can be equal to or even higher than a 5 μs standard model.
- (2)
- In the area-equivalent-based IGBT modeling method, the IGBT action process is processed for equivalence according to the predicted switching time points, so as to ensure the accuracy of output signals from the IGBT numerical model in each switching cycle, and realize the compatibility with the power modules in the Simulink by signal conversion through the controlled voltage source.
- (3)
- By case analysis, the effectiveness and efficiency of the control algorithm proposed in this paper are verified. The interpolation-prediction-based control algorithm effectively reduces the non-characteristic harmonic waves arising from switch delay, while the steadiness and transience are good. Due to the increase in simulation step, the operation efficiency of the model also significantly rises.
- (4)
- The modeling methods and control algorithm recommended in this paper apply not only to hardware in-loop simulation and real-time simulation platforms, but also to fixed-step electromagnetic transient simulation.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| RTW | real-time workshop |
| PWM | pulse width modulation |
| HVDC | high-voltage direct current |
| PSCAD | power systems computer aided design |
| uc | carrier |
| ur | modulated wave |
| i = 1, 2, 3…, n | sampling point |
| j = A, B, C | three-phase |
| ti | sampling time |
| yi | sample value of ti |
| UJn | phase voltage |
| UjO | voltage to the midpoint of the DC voltage |
| UCE | collector-emitter voltage |
| UF | simulated external voltage |
| Udc | DC-bus voltage |
| Idc | DC-bus current |
References
- Li, B.; He, J.; Li, B. A review of the protection for the multi-terminal VSC-HVDC grid. Prot. Control Mod. Power Syst. 2019, 4, 1–11. [Google Scholar] [CrossRef]
- Aleem, S.A.; Hussain, S.M.; Ustun, T.S. A Review of Strategies to Increase PV Penetration Level in Smart Grids. Energies 2020, 13, 636. [Google Scholar] [CrossRef] [Green Version]
- Shu, D.; Xie, X.; Jiang, Q.; Hang, Q.; Zhang, C. A Novel Interfacing Technique for Distributed Hybrid Simulations Combining EMT and Transient Stability Models. IEEE Trans. Power Deliv. 2018, 33, 130–140. [Google Scholar] [CrossRef]
- Albaidhani, H.; Kazimierczuk, M.K.; Reatti, A. Nonlinear Modeling and Voltage-Mode Control of DC-DC Boost Converter for CCM. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems, Florence, Italy, 27–30 May 2018; pp. 1–5. [Google Scholar]
- Ivanovic, Z.R.; Adzic, E.M.; Vekic, M.S.; Grabic, S.; Celanovic, N.; Katic, V. HIL evaluation of power flow control strategies for energy storage connected to smart grid under unbalanced conditions. IEEE Trans. Power Electron. 2012, 27, 4699–4710. [Google Scholar] [CrossRef]
- Zhang, J.; Xiong, G.; Meng, K.; Yu, P.; Yao, G.; Dong, Z. An improved probabilistic load flow simulation method considering correlated stochastic variables. Int. J. Electr. Power Energy Syst. 2019, 111, 260–268. [Google Scholar] [CrossRef]
- Huang, Q.; Vittal, V. Application of Electromagnetic Transient-Transient Stability Hybrid Simulation to FIDVR Study. IEEE Trans. Power Syst. 2016, 31, 2634–2646. [Google Scholar] [CrossRef]
- Sybille, G.; Lehuy, H. Digital Simulation of Power Systems and Power Electronics using the MATLAB/Simulink Power System Blockset. In Proceedings of the IEEE Power Engineering Society-Winter Meeting 2000 Special Technical Session, Singapore, 23–27 January 2000; pp. 2973–2982. [Google Scholar]
- Faruque, M.O.; Dinavahi, V. Hardware-in-the-loop simulation of power electronic systems using adaptive discretization. IEEE Trans. Ind. Electron. 2010, 57, 1146–1158. [Google Scholar] [CrossRef]
- Lauss, G.; Faruque, M.O.; Schoder, K.; Dufour, C.; Viehweider, A.; Langston, J. Characteristics and Design of Power Hardware-in-the-Loop Simulations for Electrical Power Systems. IEEE Trans. Ind. Electron. 2016, 63, 406–417. [Google Scholar] [CrossRef]
- Carbone, R.; Rosa, F.D.; Langella, R.; Testa, A. A new approach for the computation of harmonics and interharmonics produced by line-commutated AC/DC/AC converters. IEEE Trans. Power Deliv. 2005, 20, 2227–2234. [Google Scholar] [CrossRef]
- Bilik, P.; Zidek, J.; Kus, V.; Josefova, T. Harmonic Currents of Semiconductor Pulse Switching Converters. Energy Power Eng. 2013, 5, 1120–1125. [Google Scholar] [CrossRef]
- Wang, Q.; Wu, J.; Gao, J.; Wang, J.; Li, C.; Wang, J.J.; Zhou, N. Frequency-domain harmonic modeling and analysis for 12-pulse series-connected rectifier under unbalanced supply voltage. Electr. Power Syst. Res. 2018, 162, 23–36. [Google Scholar] [CrossRef]
- Tant, J.; Driesen, J. Accurate second-order interpolation for power electronic circuit simulation. In Proceedings of the 18th IEEE Workshop on Control and Modeling for Power Electronics, Stanford, CA, USA, 9–12 July 2017; pp. 1–8. [Google Scholar]
- Strunz, K. Flexible numerical integration for efficient representation of switching in real time electromagnetic transients Simulation. IEEE Trans. Power Deliv. 2004, 19, 1276–1283. [Google Scholar] [CrossRef]
- Shu, D.; Xie, X.; Jiang, Q.; Guo, G.; Wang, K. A Multirate EMT Co-Simulation of Large AC and MMC-Based MTDC Systems. IEEE Trans. Power Syst. 2018, 33, 1252–1263. [Google Scholar] [CrossRef]
- Faruque, M.O.; Strasser, T.; Lauss, G.; Jalili-Marandi, V.; Forsyth, P.; Dufour, C.; Dinavahi, V.; Monti, A.; Kotsampopoulos, P.; Martinez, J.A.; et al. Real-time simulation technologies for power systems design, testing, and analysis. IEEE Power Energy Technol. Syst. 2015, 2, 63–73. [Google Scholar] [CrossRef]
- Liu, X.; Cramer, A.M.; Pan, F. Generalized average method for time-invariant modeling of inverters. IEEE Trans. Circuits Syst. 2017, 64, 740–751. [Google Scholar] [CrossRef]
- Peralta, J.; Saad, H.; Dennetiere, S.; Mahseredjian, J.; Nguefeu, S. Detailed and Averaged Models for a 401-Level MMC-HVDC System. IEEE Trans. Power Deliv. 2012, 27, 1501–1508. [Google Scholar] [CrossRef]
- dSPACE Inc. dSPACE User Guide-Implementation Guide; dSPACE Inc.: Paderborn, Germany, 2005. [Google Scholar]
- OPAL-RT. RT-LAB 8.2.1 User’s Manual; Opal-RT Technologies Incorporation: Montreal, QC, Canada, 2008. [Google Scholar]
- Olimpo, A.; Acha, E. Modeling and Analysis of Custom Power Systems by PSCAD/EMTDC. IEEE Power Energy Mag. 2001, 17, 266–272. [Google Scholar]
- Pekarek, S.D.; Wasynczuk, O.; Walters, E.; Jatskevich, J.; Lucas, C.E.; Wu, N.; Lamm, P. An efficient multirate Simulation technique for power-electronic-based systems. IEEE Trans. Power Syst. 2004, 19, 399–409. [Google Scholar] [CrossRef]
- Noda, T.; Kikuma, T.; Yonezawa, R. Supplementary techniques for 2S-DIRK-based EMT simulations. Electr. Power Syst. Res. 2014, 115, 87–93. [Google Scholar] [CrossRef]
- Zou, M.; Mahseredjian, J.; Joos, G.; Delourme, B.; Gerinlajoie, L. Interpolation and reinitialization in time-domain simulation of power electronic circuits. Electr. Power Syst. Res. 2006, 76, 688–694. [Google Scholar] [CrossRef]
- Kuffel, P.; Kent, K.; Irwin, G. The implementation and effectiveness of linear interpolation within digital simulation. Electr. Power Energy Syst. 1997, 19, 221–227. [Google Scholar] [CrossRef]
- Tant, J.; Driesen, J. On the Numerical Accuracy of Electromagnetic Transient Simulation with Power Electronics. IEEE Trans. Power Deliv. 2018, 33, 2492–2501. [Google Scholar] [CrossRef]
- Faruque, M.O.; Dinavahi, V.; Xu, W. Algorithms for the accounting of multiple switching events in digital simulation of power-electronic systems. IEEE Trans. Power Deliv. 2005, 20, 1157–1167. [Google Scholar] [CrossRef]
- Liang, G.; Song, C.; Wen, S. Algorithms for the Accounting of Multiple Switching Events in Real-Time Simulation of Distributed Power. In Proceedings of the 2019 IEEE 10th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Xi’an, China, 3–6 June 2019; pp. 237–241. [Google Scholar]
- Hao, B.; Chen, L.; Akshay, K.R.; Damien, P.; Fei, G. An FPGA-Based IGBT Behavioral Model with High Transient Resolution for Real-Time Simulation of Power Electronic Circuits. IEEE Trans. Power Electron. 2019, 66, 6581–6591. [Google Scholar]
- Ji, S.; Lu, T.; Zhao, Z.; Yuan, L. Modelling of High Voltage IGBT with Easy Parameter Extraction. In Proceedings of the 7th International Power Electronics and Motion Control Conference (IPEMC 2012), Harbin, China, 2–5 June 2012; pp. 1511–1515. [Google Scholar]










| Correspondence | Logical Value |
|---|---|
| ur > uc | 1 (True) |
| ur < uc | 0 (False) |
| Project | Parameter |
|---|---|
| Step-down transformer capacity | 50 kVA |
| Rectifier grid sideline voltage | 400 V, 60 Hz |
| Inverter load sideline voltage | 380 V, 50 Hz |
| DC bus voltage | 750 V |
| Simulation Type | Step Length | The Simulation Time | The Actual Time Consumed |
|---|---|---|---|
| Standard model | 5 μs | 1 s | 13.2 s |
| Interpolation prediction model | 50 μs | 1 s | 4.5 s |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Deng, P.; Zhang, J.; Liu, D.; Hao, Z. A Study of Interpolation Compensation Based Large Step Simulation of PWM Converters. Energies 2020, 13, 3069. https://doi.org/10.3390/en13123069
Li Y, Deng P, Zhang J, Liu D, Hao Z. A Study of Interpolation Compensation Based Large Step Simulation of PWM Converters. Energies. 2020; 13(12):3069. https://doi.org/10.3390/en13123069
Chicago/Turabian StyleLi, Yahui, Pu Deng, Jing Zhang, Donghang Liu, and Zhenghang Hao. 2020. "A Study of Interpolation Compensation Based Large Step Simulation of PWM Converters" Energies 13, no. 12: 3069. https://doi.org/10.3390/en13123069
APA StyleLi, Y., Deng, P., Zhang, J., Liu, D., & Hao, Z. (2020). A Study of Interpolation Compensation Based Large Step Simulation of PWM Converters. Energies, 13(12), 3069. https://doi.org/10.3390/en13123069