Multi-Objective Optimization Model EPLANopt for Energy Transition Analysis and Comparison with Climate-Change Scenarios

Abstract

The modeling of energy systems with high penetration of renewables is becoming more relevant due to environmental and security issues. Researchers need to support policy makers in the development of energy policies through results from simulating tools able to guide them. The EPLANopt model couples a multi-objective evolutionary algorithm to EnergyPLAN simulation software to study the future best energy mix. In this study, EPLANopt is applied at country level to the Italian case study to assess the best configurations of the energy system in 2030. A scenario, the result of the optimization, is selected and compared to the Italian integrated energy and climate action plan scenario. It allows a further reduction of CO₂ emissions equal to 10% at the same annual costs of the Italian integrated energy and climate action plan scenario. Both these results are then compared to climate change scenarios through the carbon budget indicator. This comparison shows the difficulties to meet the Paris Agreement target of limiting the temperature increase to 1.5 °C. The results also show that this target can only be met through an increase in the total annual costs in the order of 25% with respect to the integrated energy and climate action plan scenario. However, the study also shows how the shift in expenditure from fossil fuels, external expenses, to investment on the national territory represents an opportunity to enhance the national economy.

1. Introduction

Energy system modeling [1] is a relevant discipline in supporting policy-makers in the definition of the energy strategy. Different European countries have already published energy strategies to meet the European climate and energy targets for 2030 [2]. Among them, there is also Italy which is selected as the case study in this paper [3].

With the aim of using an energy system model to develop different scenarios for the considered case study, the main characteristics of energy system models have been analyzed in order to choose the proper model. In particular, two features of energy system models are identified as being relevant in the scenario development process. These are the following: high temporal resolution and sector-coupling.

The hourly time-step is largely considered as high temporal resolution in energy system modeling [4]. It is particularly important when modeling energy systems with high penetration of variable renewable energy sources (VRES). Poncelet et al. [4] showed the importance of time resolution in energy system modeling. They demonstrated how the resolution in time should be prioritized compared to the resolution in techno-economic detail and how the use of a low number of time-slices (usually 12 time-slices) produces a generation mix error that cannot be considered negligible.

The second important characteristic is sector coupling. Several papers showed the advantages of sector coupling modeling compared to the single specific sector modeling approach. In this regard, it is important to mention the contribution of Aalborg University in the definition of the smart energy system concept that showed the advantages of studying the interactions and synergies between different energy sectors to maximize efficiency and reduce costs [5,6]. H. Lund in [6] and D. Connolly et al. [7] conceptualized the smart energy system definition highlighting the opportunities and synergies among different energy sectors. In [8], B.V. Mathiesen et al. analyzed the smart energy system concept focusing on the integration of the transport sector.

In [9], B. Nastasi et al. highlighted the importance of hydrogen as an energy vector to link the electricity and heating sectors. M. G. Prina et al. [10] showed the advantages of sector coupling at district heating level. R. Bramstoft et al. [11], through the studying of the decarbonization pathways of Sweden at 2050, showed the advantages of the integrated modeling of transportation, electricity, gas, fuel refinery and heat systems. S. Ben Amer et al. [12] used the Balmorel model on the Greater Copenhagen case study integrating the electricity and heating sectors. V. Heinisch et al. [13] showed the advantages of coupling the electricity, heating and transport sectors focusing on urban areas. M. Pavičević et al. [14] studied the potential of sector-coupling at European level and found out how the transport sector coupled to the power sector guarantees the highest flexibility potential in terms of power curtailment, load shedding and congestion. H. Lund et al. [15] underlined the importance of moving beyond the electricity-only approach and towards an integrated cross-sector approach.

A model which reflects these characteristics is the software EnergyPLAN [5,16,17] developed by Aalborg university [17], Denmark. EnergyPLAN software is a bottom-up single-node simulation model which allows the evaluation of different future alternatives of the energy system through the testing of different energy mixes. It implements an hourly time-step to properly describe energy systems with high penetration of renewables. Several studies coupled an optimization algorithm to the EnergyPLAN software; therefore, using the EnergyPLAN software for the simulation and dispatch over the year and an optimization algorithm for expansion capacity evaluation. This approach is largely diffuse due to the characteristics of EnergyPLAN software which requires a very short computational time. This is due to its heuristic modeling based on internal predefined priorities.

I. Batas Bjelić et al. [18] presented a single-objective (SO) optimization model coupled to EnergyPLAN and selecting the flexibility options only in the electricity sector. M. S. Mahbub et al. in [19] and in [20] presented a multi-objective (MO) optimization tool considering as flexibility options within the decision variables, only heat pumps. The EPLANopt model [21,22] developed by Eurac research through the coupling of the simulation software EnergyPLAN and a multi-objective optimization algorithm is applied at regional level in [23] selecting as flexibility options, heat pumps, batteries and power to gas. The EPLANopt tool is open-source and the full code is available at [24]. The EPLANopt model is characterized by an hourly time-step, single-node approach and by sector-coupling, i.e., the main sectors of the energy system (electricity, heating and transport sectors) are all implemented in the model. With a similar approach the EPLANopt model is applied in this study at the Italian energy system.

In particular, the aim of this paper is the following: (i) the creation of an energy system model which reflects the Italian integrated energy and climate action plan at 2030 (Piano Nazionale Integrato Clima e Energia—PNIEC [3]). This is useful to validate the model on the achievement of the energy targets and at the same time to estimate the total annual costs of the energy system. This latter is important information for the comparison with different scenarios. (ii) Through the expansion capacity optimization model, EPLANopt, this work aims to inspect future scenarios under total annual costs and CO₂ emissions minimization. The comparison of these scenarios with the Italian integrated energy and climate action plan allows the understanding of other alternatives to the energy system able to further decrease CO₂ emissions. (iii) The last scope is to compare the scenarios, result of the optimization process and the Italian integrated energy and climate action plan scenario with the climate change scenarios. Through this comparison the aim is to understand if these scenarios are in line with the Paris Agreement target [25] of limiting the temperature increase to 1.5 °C. This comparison is possible thanks to the use of the carbon budget indicator.

One challenge of energy system modeling is the connection between bottom-up energy system models and the impacts of energy transition on the environmental sphere. Considering climate change scenarios in energy system modeling is usually performed through the integration of top-down and bottom-up approaches with different degrees of linking between the two methodologies. For example, M. Rocco et al. [26] realized a soft-link between the open-source energy optimization model (OSEMOSYS) and a linear input-output model (IO) to evaluate the environmental impact of future energy scenarios. S. D. Tuladhar [27] realized a hard-link between a bottom-up and top-down model by means of an iterative process with the aim of climate change analysis. Other examples of hybrid models, results of the integration between bottom-up and top-down, are integrated assessment models (IAMs) [28] which present close loops between climate, impacts, economy and energy modules. This paper aims at implementing a simplified and fast method to connect the results of a bottom-up energy system model with climate change scenarios. Future steps will be dedicated to the integration of EPLANopt with a top-down model to assess the impacts on the economy and the environment.

The paper has the following structure: a materials and methods section presents the EPLANopt model, its main characteristics and the carbon budget indicator; a section on the Italian case study presents the assumptions and sources of the input data used for the case study; a results section shows the outcomes of the model and conclusive remarks are given in the last section. The work presented in this paper received funding from the FESR 1042 “Integrids” project and by institutional funding. The funding body did not influence the case study, assumptions or the choice of the model.

2. Materials and Methods

The materials and methods section is structured as follows: (i) the EPLANopt model, why it is chosen and its main characteristics; (ii) EnergyPLAN software main general features; (iii) explanation of the multi-objective optimization analysis used in EPLANopt; (iv) specific characteristics of the EnergyPLAN software to this particular case study and (v) the carbon budget methodology and how the results from the bottom-up energy system model EPLANopt are connected to climate change scenarios.

EPLANopt [21,22] is a bottom-up short-term energy system model which is selected because it allows the implementation of multi-objective optimization without losing resolution in time and in sector-coupling [29], which, as already mentioned, are relevant characteristics for describing energy systems with high penetration of renewables. Bottom-up models accurately describe the energy system internal relationships and allow the user to evaluate the future alternatives of the energy system and the potential synergies between energy sectors. These models do not usually describe the interactions between the energy sectors and the economics of a nation, region or municipality. These models differ from the top-down approach [30] which instead are characterized by less details in the energy sector but describe the relations with other interconnected sectors such as employment, social growth, public welfare, et cetera. Short-term models inspect the alternatives of the energy system in a future target year. These differ from long-term models [31] which study and assess the entire transition between the current state of the energy system up to a future target year.

The EPLANopt model is the result of a coupling between the EnergyPLAN software [5,16,17] and an expansion capacity optimization algorithm. The EnergyPLAN software is a deterministic simulation model, it is suited to describe future scenarios with high penetration of VRES, it simulates a one-year period with an hourly time-step and it integrates the three primary sectors of the energy system. The model was applied at different scales: at European level [32], at national level [33,34,35,36,37,38,39,40], at regional level [41], to towns and municipalities [10,42] and to small islands [43,44,45].

The multi-objective expansion capacity optimization algorithm is based on a multi-objective evolutionary algorithm (MOEA) [46,47,48] which allows the assessment of the Pareto front of optimal solutions. The multi-objective approach allows the modeler to find optimal solutions in terms of simultaneous minimization or maximization of different indicators. Therefore, the multi-objective optimization approach allows the simultaneous assessment not only of an economic objective, as usually adopted in single-objective expansion capacity optimization problems, but also considering an environmental one. The considered objectives for this particular case are the minimization of the total annual costs and the minimization of annual CO₂ emissions. Equation (1) shows the objective functions of the multi-objective minimization problem. The main constraints describe how the value of the decision variables should remain in a fixed range defined by the decision variables’ lower $D{V}_i^{(L)}$ and upper $D{V}_i^{(U)}$ bounds. Other constraints such as balance between demand and generation at each time-step or storage behavior with initial content equal to final content are defined within the EnergyPLAN software.

$$\mathrm{Optimization}\mathrm{function}min\left(\begin{array}{c}Annual\_Costs \left[\mathrm{M}€\right] \\ Annual\_C{O}_2\_Emissions \left[\mathrm{Mt}\right] \end{array}\right)$$

(1)

$$\mathrm{Subject}\mathrm{to}D{V}_i^{(L)}\le D{V}_i\le D{V}_i^{(U)}$$

The operational simulation of the year is performed through EnergyPLAN software while the expansion capacity optimization is achieved through the MOEA. The total annual costs are considered by EnergyPLAN as the sum between annualized investment costs, fixed operation costs and variable costs. These latter are divided into fuel costs and electricity exchange costs.

The MOEA creates an initial population of random individuals. The population is the set of different solutions which will be tested by the optimization algorithm to find the optimum. Each individual is made up of a list of values for the decision variables. For each decision variable, the value is found in the range defined by a minimum, $D{V}_i^{(L)}$, and a maximum bound, $D{V}_i^{(U)}$. The MOEA then inspects and evaluates each solution (thus each individual) by running the simulation model, in this case EnergyPLAN. EnergyPLAN is run on the selected future target year, replacing the values of the decision variables which characterized the solution in the EnergyPLAN input file of the baseline. EnergyPLAN returns the values of different indicators. Two of them, total CO₂ emissions and total annual costs, are chosen as objective functions. Each individual or solution is compared to the others based on these two indicators. Through the use of operators typical of genetic algorithms (such as selection, crossover and mutation) the optimization algorithm moves forward creating a new population of individuals. These steps are repeated until the convergence is reached and the final Pareto front is found.

EnergyPLAN is adopted in this study with the following specific characteristics: (i) The version is 12.1; (ii) the technical simulation option is selected; (iii) dump charge is chosen for electric mobility; and (iv) power-to-gas is modeled through two main variables, the hydrogen produced and the capacity of the electrolyzer. The electrolyzer will start producing hydrogen in the time-step in which there is over-generation of electricity from VRES and injecting it into the gas grid. This is implemented in EnergyPLAN through the electro-fuels sheet; CO₂ hydrogenation section, by setting to zero the parameters of the carbon recycling and the electrolyzer efficiency equal to 0.7. The variables SynGridGas [TWh/year] under output section, which corresponds to the produced hydrogen, and the MaxCap variable under the flexibility section, which represents the capacity of the electrolyzer are chosen within the optimization. The decision variables are the technologies on which the expansion capacity optimization analysis is performed. These two variables, produced hydrogen and capacity of the electrolyzer, are chosen as decision variables together with a list of other technologies such as variable renewable energy sources, electric storage, et cetera. The complete list is introduced in Section 3. The optimization algorithm varies their values in order to find the best energy mix for the considered case study, hence, finding the right combination of excess electricity production, size of the electrolyzer, produced hydrogen, et cetera.

As mentioned in the introduction, the aim of the paper is also to connect and compare the scenarios obtained through the optimization methodology to climate-change scenarios. In order to achieve this task, there is the need to introduce the remaining carbon budget concept. It is defined by J. Rogelj et al. [49] as the “Finite total amount of CO₂ that can be emitted into the atmosphere by human activities while still holding global warming to a desired temperature limit”. In [49], J. Rogelj et al. estimate the remaining carbon budget on a global level equal to 480 Gt CO₂. This amount represents the overall quantity of CO₂ emissions that can be emitted for a 50% probability of limiting global warming to 1.5 °C (within 2100 above pre-industrial levels, 1850–1990). Assuming that each person on earth has the same carbon budget, the overall carbon budget for the considered case study, Italy, results in 3.8 Gt.

3. Italian Case Study

This section is dedicated to the description of the input data and assumptions regarding the selected case study. It is structured as follows: (Section 3.1) The first section concentrates on the baseline, the required data for its characterization and the assumptions. The baseline is a scenario which reflects the current state of the energy system for a reference year. (Section 3.2) The second section focuses on the Italian integrated energy and climate action plan and its definition in the EnergyPLAN software. (Section 3.3) The third section describes the decision variables and their ranges. The decision variables are the technologies on which the expansion capacity optimization analysis is performed. Their ranges define the domain of the optimization problem. For each decision variable the range is defined by a minimum bound, the value in the reference year and a maximum bound, the maximum potential for the source. Moreover, this section explains the assumptions introduced on energy efficiency of buildings, electric mobility, energy efficiency in the industry sector, et cetera. (Section 3.4) The fourth section defines the optimization problems and their assumptions.

3.1. Baseline

The first step consists of the creation of the Baseline which is the scenario reproducing the Italian energy system for a specific reference year. In this study the reference year is 2015 and the application case study is the Italian energy system. The created scenario is called Baseline 2015. It is characterized by an input file of EnergyPLAN which collects all the information of the Italian energy system for the year 2015: energy demand, installed power and capacity of different sources, efficiencies, emission factors, fuel costs, investment and operation and maintenance (O&M) costs.

The Baseline 2015 is created by the Heat Roadmap Europe 4 (HRE4) project [50] which provides the 2015 EnergyPLAN input file for 14 EU member countries (Italy included) [51]. This 2015 HRE4 baseline is modified using more precise data taken from Italian authorities: GSE [50], RSE [52] and Terna [53].

Table 1. Sources used for the development of the 2015 baseline for Italy.

Sector	Data	Source	References
Electricity	Capacity of renewables	GSE	[54]
	Hourly profile for renewables	Terna, GSE	[53,54]
	Capacity for other technologies	Terna	[55]
	Electricity demand	Terna, HRE	[50,53]
Heating	Generation and consumption data	HRE	[50]
Mobility	Consumption data	HRE	[50]
	Electric vehicles demand and charge profile	RSE	[52]

summaries the main open sources used to collect the input data divided into the electricity, heating and mobility sectors. The data are mainly generation and consumption data, thus including capacities, efficiencies and time-series.

The electricity sector produced by HRE4 is the most modified and adapted in this work. M. Noussan et al. [56], starting from open data, presented a data analysis of the electricity generation at the Italian level, by considering some performance indicators based on primary energy consumption, share of renewable energy sources and CO₂ emissions. The same open data sources are used to update the EnergyPLAN input file for the Italian case study in 2015.

Renewable energy installed power is taken from the statistic report of GSE (Italian authority on renewable energy and energy efficiency) [54]. Hourly distributions profiles of renewable energy sources are taken from Terna transparency reports [53]. Terna is the Italian transmission system operator. However, these distributions are influenced by the commissioning and entry into service of new plants during the year. This affects the hourly distribution because, at the end of the year, the generation is characterized by a different installed capacity from the one at the beginning of the year. In order to get rid of this increasing factor, a linear increase of the installed capacity of each renewable energy source is assumed between the beginning and end of the year. The artificial value of capacity in each time-step $t$ is given by Equation (2). $C_{m,t}$ is the capacity of technology $m$ at time-step $t$. $C_m^{start}$ is the capacity of technology $m$ at the beginning of the considered year while $C_m^{end}$ is the capacity of technology $m$ at the end of the considered year. 8784 are the hours in a year (EnergyPLAN considers a leap year).

$$C_{m,t}=C_{m,t-1}+t·\frac{C_m^{start}-C_m^{end}}{8784}$$

(2)

The generation of each renewable energy source in each time-step $t$ is rescaled to take into consideration this increase in capacity over the year. Equation (3) shows the new hourly power output of technology $m$. ${P^{\prime }}_{m,t}$ is the new rescaled power output of technology $m$. $P_{m,t}^{Terna}$ is the old power output of technology $m$ taken from the Terna data (values that should be purged from the increasing capacity over the year).

$${P^{\prime }}_{m,t}=P_{m,t}^{Terna}\cdot \frac{C_m^{end}}{C_{m,t}}$$

(3)

The new generation value is equal to the equivalent power output that would have been produced in the time-step $t$ by the total capacity installed at the end of the year. Another modification of the existing Heat Roadmap Europe data is required: the equivalent hours of the hourly distribution must coincide with the value from GSE. Equivalent hours express the full load hours of a certain source. Equation (4) shows how the equivalent hours are calculated, where $P_m$ is the total power output of technology $m$ over the year and $C_m$ is the capacity of technology $m$.

$$h_{eq,m}=\frac{P_m}{C_m}$$

(4)

Table 2. Equivalent hours for renewable energy sources in Italy: Photovoltaic (PV), wind power, river hydro and geothermal. Values from 2011 to 2015.

Equivalent Hours	PV	Wind Power	Hydro (River)	Geothermal
Equivalent hours 2011	1325	1563	4060	7324
Equivalent hours 2012	1312	1855	4379	7243
Equivalent hours 2013	1241	1793	4392	7321
Equivalent hours 2014	1211	1767	4454	7206
Equivalent hours 2015	1225	1683	4374	7534
Average equivalent hours	1263	1732	4332	7325

shows the equivalent hours of the main Italian renewable energy sources and the final five year average value. This average value is chosen for the modification of the hourly distribution data with the aim to reconcile the year by year variability of these renewable energy sources.

The method to correct the hourly distribution data is taken from the EnergyPLAN documentation. This method is shown in Equation (5) where $FA{C}^{RES}$ is a correction factor. This value is unknown and has to be found in order to obtain a value of equivalent hours for the new distribution equal to the average equivalent hours of Table 2.

$$P_{m,t}={P^{\prime }}_{m,t}\cdot \frac{1}{1-FA{C}^{RES}·(1-{P^{\prime }}_{m,t})}$$

(5)

A last modification that needs to be done is caused by the EnergyPLAN leap year approach. In order to generate hourly distributions of 8784 elements it is necessary to create an imaginary 29th February for the year 2015. This day is created by copying the previous day’s distributions.

Once all of these modifications are implemented, it is possible to calculate the hourly distributions to be used in EnergyPLAN (Equation (6). $P_m^{nom}$ is the nominal power or installed capacity of technology $m$ in the year 2015. $P_{m,t}^{ePLAN}$ is the final hourly distribution with values between 0 and 1.

$$P_{m,t}^{ePLAN}=\frac{P_{m,t}}{P_m^{nom}}$$

(6)

Figure 1 shows an elaboration of the hourly distributions for PV, wind power, geothermal and river hydro in the years from 2011 to 2015. The representative day for each month is implemented calculating the average of the values of the same hours on all the days of that month. This type of graph is useful to highlight seasonal and intra-day variability. It shows the potential integration between PV and wind power. In fact while PV has a higher generation in summer wind power produces the most in the winter season. Geothermal is almost constant and river hydro has its peak during the end of spring and the beginning of summer. It is important to highlight that the seasonal variability of river hydro could change in the future as a result of climate change and melting of the glaciers [57]. The installed power of PV in 2015 was equal to 18,892 MW. Wind power installed power was 9162 MW and geothermal was 821 MW. Hydro power is divided into three categories: pumped hydro storage, reservoir hydro power and river hydro. River hydro is characterized by a small reservoir in the order of a few hours. The installed power of river hydro was equal to 5332 MW in 2015. As it is possible to see from Figure 1, the river hydro profile has a daily cycle with two peaks: one in the morning and the other one in the evening. This is typical of the daily electricity demand profile and suggests that these plants within the day can modulate their production in response to the demand and the prices of electricity.

Other renewable energy sources such as biomass plants and reservoir hydro power can modulate their output power. Biomass power plants’ installed capacity in Italy is equal to 4057 MW. In this work, biomass power plants are modeled within VRES using a constant distribution profile. In support of this assumption, these types of plants, even if potentially they can produce and modulate their power to follow the load, are usually forced to produce at maximum constant output power in order to exploit the maximum of their abilities. Equation (7) shows how the new artificial capacity ${C^{\prime }}^{bio}$ is calculated. $C^{bio}$ was the actual capacity for biomass power plants in 2015. $h_{eq}^{bio}$ expresses the actual equivalent hours of biomass power plants and 8784 are the total hours in a leap year. The CO₂ emissions from biomass are considered zero (as in the Heat Roadmap Europe baseline and scenarios).

$${C^{\prime }}^{bio}=C^{bio}\cdot \frac{h_{eq}^{bio}}{8784}$$

(7)

Reservoir hydro power was characterized by an installed power of 9425 MW in 2015. In EnergyPLAN, reservoir hydro power has a dedicated component. However, this component is used to model pumped hydro storage; thus, like the biomass power plants, reservoir hydro power is modeled into the VRES category assuming a constant hourly profile of generation. Equation (7) is applied to reservoir hydro power to find the new artificial capacity.

Italian fossil fuel power plants are constituted mostly of combined cycle gas turbine (CCGT) systems burning natural gas. These plants have the highest efficiencies among fossil fuel power plants and are also flexible in load modulation. However, the increase in electricity generation from renewables has brought a reduction in the utilization of these systems with a drastic drop in recent years of their equivalent hours [58] (from 4000–6000 to 1000–2000 hours). Fossil fuel power plants are modeled in EnergyPLAN in the power plant (PP2) component with a value of overall capacity taken from Terna [59], a value of average efficiency taken from Heat Roadmap Europe [52] and the relative quantities of each type of burnt fuel. The overall fossil fuel power plants installed capacity of the 2015 Italian energy system is 63,863 MW, the sum of the installed capacity of CCGTs and coal power plants. The efficiency of the average fossil fuel power plant is 0.455 and the percentages of burnt fuel types are the following: 39% coal and 61% natural gas.

For electricity storage the only technology present in the energy system of 2015 was pumped hydro storage. This technology has already reached its maximum potential and for future installation of electric storage other technologies must be taken into account. In Italy, in 2015, the pumped hydro-storage installed plants allow the achievement of 700.76 GWh of available storage capacity, 6175 MW of pumps and 7815 MW of installed turbines. These data are the aggregated results of internal analysis developed by Politecnico di Milano. The average charging efficiency is set at 0.85 while the average discharging efficiency equal to 0.9. S. Mazzoni et al. [60] investigated the techno-economic impact of different storage technologies demonstrating how the use of these technologies leads to primary energy savings and high efficiency.

The overall electricity demand is the sum of various contributions: the generic electricity demand, electricity demand from the heating sector, electricity demand from the cooling sector and electricity demand from the mobility sector. Figure 2 shows the representative day per month of the overall electricity demand in the years from 2011 to 2015. It is possible to observe the two-peak daily profile, one in the morning and one in the evening. The highest values of electricity demand are in July when cooling requirements become more relevant. The total electricity demand in 2015 is equal to 316.9 TWh after transmission losses deduction, Terna data [55].

For the heating and cooling sector, M. Noussan et al. [61] presented an insightful analysis on building heating systems for the most populated Italian region by means of open data. However, from a national perspective there is a lack of updated open data. Therefore, the Heat Roadmap Europe 2015 baseline is taken as it is without changes. Few modifications in the mobility sector are implemented instead. Benini et al. [52] analyzed the Italian mobility sector identifying an electricity demand from the mobility sector in 2015 equal to 0.87 TWh. The same report also provides the hourly distribution of electricity demand from electric mobility (shown in Figure 3). This profile is assumed to be the same for each day of the year.

In 2015, Italy imported 43.7 TWh of electricity [53]. This is modeled in EnergyPLAN through the import component that allows setting the total amount of import and its hourly distribution during the year.

The Italian EnergyPLAN Baseline 2015 is validated comparing the final CO₂ output emissions with the amount estimated by different references shown in Figure 4. These values span from a minimum of 330.7 t of CO₂ emissions reported by the International Energy Agency [62] to a maximum of 339.95 estimated by the UNFCCC [63]. The value obtained after creating and running the EnergyPLAN Baseline 2015 input file is equal to 334.7 t of CO₂ emissions and thus fully included in the range given by the different analyzed sources.

3.2. PNIEC 2030 Scenario

The second step is the definition of the EnergyPLAN input file for the Italian integrated energy and climate action plan [3]. All the input values are taken from the Italian integrated energy and climate action plan document. The resulting scenario is called PNIEC 2030 scenario. The major transformations regard the electricity sector in which an increase of renewable energy penetration is foreseen, mainly photovoltaics and wind power technology, capable of covering 55% of gross final electricity consumption. The same indicator for the baseline year is equal to 34%. Moreover, the PNIEC 2030 scenario implements 40 GWh of stationary batteries. It is characterized by 10% penetration of electric mobility and an increase of the consumption of advanced biomethane in the transport sector. It also foresees an increase of energy efficiency of buildings equal to 15% by 2030.

3.3. Decision Variables and Assumptions

The third step is the definition of the decision variables and their ranges. This information is provided by

Table 3. List of decision variables and their lower $D{V}_i^{(L)}$ and upper $D{V}_i^{(U)}$ bounds.

Decision Variables	$\mathit{Current}\mathit{Value}\left(2015\right),\mathit{D}{\mathit{V}}_{\mathit{i}}^{(\mathit{L})}$	$\mathit{Maximum}\mathit{Potential}\mathit{D}{\mathit{V}}_{\mathit{i}}^{(\mathit{U})}$
Residential PV (GW)	15	120
Utility scale PV (GW)	4	70
Wind power (GW)	9	49
Lithium-ion batteries (GWh)	0	600
Power to gas, H2 produced (%)	0	15
Power to gas, Electrolyzer max capacity (GW)	0	30
Advanced biomethane (TWh)	3	15
Energy efficiency of buildings (%)	0	75
Heat pumps (%)	0	100

. The choice of the decision variables is driven by the technologies which the Italian integrated energy and climate action plan concentrates on. They are rooftop PV, utility scale PV, wind power, lithium-ion batteries, power-to-gas, advanced bio-methane in the transport sector and energy efficiency of buildings and heat pumps in the heating sector.

The maximum potential is determined for each VRES through an analysis of the technical availability of installable capacity. For other variables such as lithium-ion batteries and power-to-gas electrolyzers, a number large enough to perform the optimization and small enough not to enlarge the domain of the optimization too much by increasing the computation time without an added value was selected. The assumptions on the potential are the following:

• Solar PV. For residential rooftop PV a couple of studies, Taylor et al. [67] and Vartiainen et al. [68], together with internal studies of Eurac research based on the Solar Tyrol project [69] identified a share of 2 kW per person as the maximum rooftop PV potential. Considering roughly 60 million inhabitants in Italy the final maximum potential for residential PV is assumed to be 120 GW. For what concerns utility scale PV, the maximum potential is taken from a study of the Energy Strategy Group [70] which studied the potential for the Italian territory evaluating the brownfield sites and unutilized rural areas. The overall estimated value is equal to 70 GW. An analysis of the land use for solar power by 2030 was realized by F. Mancini et al. [71]. They demonstrated how the use of 10% of the soil already consumed could be sufficient to achieve the set objectives by 2030.
• On-shore wind power. Hoefnagels et al. [72] in the framework of the RE-shaping project estimated a maximum potential of 49 GW for Italy.
• Lithium-ion batteries. The maximum potential is evaluated through a series of simulations. A value above 600 GWh brings higher costs without any benefits in terms of renewable energy integration.
• Power to gas is managed through two variables: the produced hydrogen and the capacity of the electrolyzer. The produced hydrogen maximum potential is assumed to be 15% of the overall natural gas consumption. The maximum size of the electrolyzer is taken high enough to exploit the full potential of power-to-gas and low enough to contain the domain of the optimization problem.
• The installation of heat pumps is allowed only after a deep energy refurbishment of buildings. This decision variable is the percentage of the overall buildings that switched their heating system from boilers to heat pumps. For this reason, its maximum potential is 100%.
• The energy efficiency of buildings: the potential of energy efficiency by means of passive solutions is bound to the energy efficiency cost curve and is equal to 75%. The energy efficiency cost curve and the way it is implemented in the source code of EPLANopt is explained in a previous publication [21].

Other assumptions in the heating sector are: domestic hot water (DHW) in buildings reached by district heating network is supplied by district heating itself. For the other individual buildings, only the heating demand can be reduced through energy efficiency refurbishment, while DHW share instead is not influenced by energy efficiency and kept constant. The optimization decides which share of renovated buildings should install heat pumps. In the individual sector, at the increase of the energy efficiency share, heat pumps substitute different types of boilers with the following priorities: (1) coal boilers, (2) oil boilers, (3) electric boilers, (4) natural gas boilers and (5) biomass boilers. A more detailed explanation of the modeling approach taking into account energy efficiency of buildings is provided by previous studies [21,23].

The costs related to electric mobility is considered in the model. Starting from the study of the Enel foundation [73], the cost of the electric vehicles (EV) infrastructure is estimated for different shares of penetration of battery electric vehicles (BEV). Figure 5 shows these costs which increase linearly at the increasing of the EV penetration. These costs take into account the infrastructural costs of electric mobility for urban and sub-urban areas and the costs for different type of charging stations.

The model also considers a decrease in energy consumption from the industry sector. Starting from the historical data provided by the Odyssee-Mure database [74] a logarithmic interpolation is implemented to inspect the business as a usual scenario for energy efficiency in the industry sector. The value is integrated in the model which therefore considers 9% of energy efficiency in the industry sector with respect to the energy consumption of 2015, the year of the baseline (See Figure 6).

Additional assumptions are the following: (i) constant demographic situation from 2015 to 2030; (ii) export price for electricity equal to 35 €/MWh [75]; (iii) import price for electricity equal to 45 €/MWh [75]; (iv) emission factor of imported electricity equal to 270 kg/MWh [76] in 2030. (v) The electricity generation from river hydro is assumed to slightly increase from 23.1 to 24.8 TWh, while the generation from dammed hydro remain constant [3]. The generation from geothermal increases from 6.0 to 7.1 TWh [3]. The electricity production from biomass power plants decreases from 19.4 to 15.7 TWh [3]. (vi) Transport demand in terms of driven km and modal split is assumed constant, (vii) power to gas costs are those of the electrolyzer installed capacity (400 €/kW, lifetime = 15, O&M = 3% of the investment cost). Other costs of the power to gas flexibility option are not included because the injection of hydrogen goes directly into the existing gas grid.

3.4. Optimization Problems Definition

The fourth step is the definition of the optimization problems interesting to the current analysis. Two optimization problems are formulated to study the impact of different levels of penetration of electric mobility. The electric mobility share is set as an exogenous variable and the optimization problem is run to find the optimal solutions under the considered assumptions. The evaluated optimization problems are the following:

-

One case considering 10% electric mobility

-

One case considering 20% electric mobility

Different levels of penetration of electric mobility are considered by simply introducing some conversion factors in kWh/100 km for each fuel based vehicle [77] assuming the transport demand in terms of driven km is constant. The values used are the following: 52.78 kWh/100 km for petrol fuelled cars, 46.11 kWh/100 km for gasoil fuelled cars and 13.61 kWh/100 km for electric vehicles. The use of these conversion factors allows the evaluation of the electricity demand generated from electric mobility. This value is set in EnergyPLAN in order to evaluate the hourly operational simulation and the impacts on the overall energy system.

4. Results

The results of the two optimization problems are depicted in Figure 7. It shows the Baseline 2015, the PNIEC 2030 and the Pareto fronts of optimal solutions for the cases with 10 and 20% electric mobility penetration. One scenario is selected on the 20% electric mobility Pareto front with the same costs of the PNIEC 2030 scenario. It is named Advanced 2030. The graph allows the following remarks:

(i)

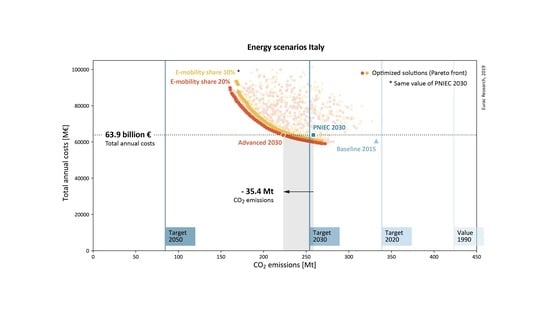
The PNIEC 2030 scenario produces a relevant reduction of CO₂ emissions compared to the Baseline 2015. This reduction is in line with the CO₂ emissions reduction target in 2030. The PNIEC 2030 scenario is found by Italian authorities through an optimization process but the assumptions on costs and efficiencies of the energy system components are not public. Therefore, it is important to validate the model and the PNIEC 2030 scenario. This result allows this validation which is added to the validation of the Baseline 2015 on CO₂ emissions.

(ii)

The PNIEC 2030 scenario, characterized by 10% electric mobility penetration, is almost placed on the Pareto front characterized by 10% electric mobility. Thus, it is a solution close to the optimum. As already mentioned, the PNIEC 2030 scenario is found as a result of an optimization process by Italian authorities. In this study, the difference between the PNIEC 2030 scenario and the Pareto front with 10% electric mobility can be a consequence of different costs assumptions.

(iii)

With the same cost of the PNIEC 2030 scenario it is possible to reach higher CO₂ emissions reduction by selecting a solution on the Pareto front with 20% electric mobility. The Advanced 2030 scenario showed that at the same costs of the PNIEC 2030 there are solutions which further reduce the CO₂ emissions. In this case the Advanced 2030 scenario produces a further reduction of 10%.

(iv)

Another consideration that needs to be done is on the impact of electric mobility. The increase of electric mobility from 10 to 20% together with the optimal energy mix found by the optimization algorithm allows a further reduction of the CO₂ emissions.

The analysis of the results focuses on the Advanced 2030 scenario and on the comparison with the PNIEC 2030 and Baseline 2015. In particular, the comparison of the scenarios with similar costs (PNIEC 2030 and Advanced 2030) allows the study of the best choices to decarbonize the energy system.

Table 4. Values of the main technologies in the different scenarios.

Scenarios	PV	Wind Power	Stationary Batteries	Batteries of EV	Advanced Biomethane	Energy Efficiency of Buildings
Baseline 2015	19 GW	9 GW	0 GWh	0 GWh	3 TWh	0%
PNIEC 2030	59 GW	23 GW	40 GWh	200 GWh	15 TWh	15%
Advanced 2030	86 GW	48 GW	0 GWh	400 GWh	3 TWh	30%

shows the characteristics of the considered scenarios with the comparison of the values of the main decision variables. This shows how the Advanced 2030 scenario, when compared to the PNIEC 2030 scenario, presents a higher installed capacity of VRES and higher energy efficiency of buildings, with a lower value of capacity of stationary batteries and advanced biomethane production. Another difference is the penetration of electric mobility: 10% for the PNIEC 2030 scenario and 20% for the Advanced 2030 scenario. This results in an overall aggregated capacity of batteries in the electric vehicles which is higher in the Advanced 2030 scenario. The value of the installed capacity of batteries for electric vehicles is calculated to give an idea of the overall size. The assumptions for this calculation are the following: 39 million cars are considered and an average size of 50 kWh battery per car [78].

Figure 8 shows the evolution of the electricity demand in a week in summer and in winter for the three solutions: Baseline 2015, PNIEC 2030 and Advanced 2030. It is possible to observe the increase of electricity demand due to energy efficiency of buildings and the substitution of electric boilers with heat pumps and electric mobility. Power-to-gas electricity demand is equal to zero because the optimization does not choose it to decarbonize the energy system. The main reason is the limited amount of available over-generation from renewables that can be used by power-to-gas for the hydrogen generation. This over-generation can be noted in Figure 9 which shows the electricity generation from the different sources. The over-generation is present mostly in summer and partly exploited by the existing pumped hydro storage systems.

Figure 10 shows the annual electricity generation from different sources for the tree different scenarios. The electricity generation from coal disappears in the PNIEC 2030 and Advanced 2030 scenarios due to the coal phase-out foreseen by the Italian integrated energy and climate action plan can be noted. The Advanced 2030 scenario is characterized by higher installed power of VRES and therefore a lower generation from gas power plants. The electricity demand is equal to 315.7 TWh in the Baseline 2015, 340 TWh in the PNIEC 2030 scenario and 343.6 TWh in the Advanced 2030 scenario. This is due to the higher share of electric mobility and energy efficiency of buildings with heat pumps installation in the Advanced 2030 scenario.

Figure 11 shows the annual energy consumption for the scenarios Baseline 2015, PNIEC 2030 and Advanced 2030 with the percentages of renewables for each sector. Compared to the PNIEC 2030 scenario, the Advanced 2030 scenario is characterized by higher renewable energy sources (RES) share in the electricity sector coupled to an electrification of the heating and transport sector.

Figure 12 shows the total annual costs structure in the three considered scenarios: Baseline 2015, PNIEC 2030 and Advanced 2030. The Advanced 2030 compared to the PNIEC 2030 shows a reduction of the fossil fuel costs and an increase in the costs of VRES installed power and energy efficiency of buildings.

Figure 13 allows a consideration on the nature of the costs which change in these three scenarios. Moving from the Baseline 2015 to the Advanced 2030 scenario, the costs for fossil fuels decrease and the possible domestic value creation increases. This latter represents the possible investments in the territory which could boost the local economy.

In Section 2 the remaining carbon budget value is estimated for Italy. Figure 14 shows (i) the historical trend of CO₂ emissions of Italy from 1990 to 2018, (ii) the remaining carbon budget assuming a linear decrease from the value of 2018, (iii) the PNIEC 2030 and Advanced 2030 scenarios. The graph shows how the CO₂ emissions reduction in the PNIEC 2030 is not in line with the carbon budget limit. This is assuming a linear decrease of the CO₂ emissions. Following the trajectory of the PNIEC 2030 would require a drastic decrease of the emissions after 2030. The results show that the Advanced 2030 scenario improves the CO₂ emissions reduction compared to the PNIEC 2030, but it is still higher than the carbon budget limit, assuming a linear reduction.

This highlights the necessity of a more drastic transition. This can be achieved through the selection of an optimized scenario, among those obtained through the EPLANopt multi-objective method, with higher total annual costs and lower CO₂ emissions. Knowing the carbon budget limit, it is possible, thanks to the Pareto curve, to identify the scenario in line with the carbon budget. This scenario would require an increase of the total annual costs compared to the integrated energy and climate action plan scenario equal to about 25%.

5. Conclusions

The EPLANopt model allows the multi-objective investment optimization of the energy system. It is based on the EnergyPLAN model which considers an hourly time resolution and a sector-coupling approach. The EPLANopt energy system model is applied to the Italian case study to compare the Italian integrated energy and climate action plan (PNIEC 2030 scenario) with scenarios obtained through the optimization process.

Among the optimized scenarios, one with costs similar to the Italian integrated energy and climate action plan scenario is identified (Advanced 2030 scenario). It allows a further reduction of CO₂ emissions equal to 10% at the same annual costs. The integrated energy and climate action plan and the optimized scenario with the same costs were compared in the analysis of the results. The optimized scenario presents a higher share of renewables in the electricity sector together with a higher degree of electrification of the heating and transport sectors. It is important to underline that the difference between the Advanced 2030 scenario and the PNIEC 2030 scenario can arise from different costs assumptions.

The two scenarios were compared to climate-change scenarios through the use of the carbon budget concept. The results highlighted how both the integrated energy and climate action plan scenario and the Advanced 2030 scenario are far from the carbon budget limit. The results show that the Advanced 2030 scenario improves the CO₂ emissions reduction if compared to the integrated energy and climate action plan scenario, but it is not enough to meet the carbon budget limit. In order to meet this target, there is the need for a more drastic scenario in terms of CO₂ emissions reduction. Moving on to the Pareto front it is possible to select the first optimal scenario in line with the CO₂ emission reduction driven by the carbon budget limit, assuming a linear decrease, and with the lowest costs. This scenario requires an increase of the overall costs equal to 25% with respect to the integrated energy and climate action plan scenario.

The results also showed the economic opportunity represented by energy transition. The study of the nature of the costs showed how, moving from the Baseline 2015 to the Advanced 2030 scenario, the costs for fossil fuels decrease and the possible domestic value creation increases. This represents an opportunity of development of investments in the territory and a boost to local economy. Therefore, even if the study showed the need for an energy system characterized by higher costs compared to the Baseline 2015, it also highlighted the opportunities represented by the energy transition.

Future steps will concentrate on the integration of the bottom-up EPLANopt model with a top-down approach in order to evaluate the different policies needed to support the energy transition. This integration of a top-down into a bottom-up approach will also allow a more detailed analysis of the nature of the expenses and investments of the energy system evaluating the impacts on the territory and the local economy.