Next Article in Journal
Degradation of Hydrophobic, Anti-Soiling Coatings for Solar Module Cover Glass
Previous Article in Journal
Decarbonization of Australia’s Energy System: Integrated Modeling of the Transformation of Electricity, Transportation, and Industrial Sectors
Previous Article in Special Issue
The Effect of Inclination Angle and Reynolds Number on the Performance of a Direct Contact Membrane Distillation (DCMD) Process
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 13
Issue 15
10.3390/en13153815
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Multicomponent Shale Oil Flow in Real Kerogen Structures via Molecular Dynamic Simulation

by
Jie Liu
1,2,
Yi Zhao
3,
Yongfei Yang
1,2,*,
Qingyan Mei
3,
Shan Yang
3 and
Chenchen Wang
4
1
Key Laboratory of Unconventional Oil and Gas Development, China University of Petroleum (East China), Ministry of Education, Qingdao 266580, China
2
Research Centre of Multiphase Flow in Porous Media, School of Petroleum Engineering, China University of Petroleum (East China), Qingdao 266580, China
3
Exploration and Development Research Institute of PetroChina Southwest Oil and Gas Field Company, Chengdu 610041, China
4
Hubei Cooperative Innovation Centre of Unconventional Oil and Gas, Yangtze University, Wuhan 430100, China
*
Author to whom correspondence should be addressed.
Energies 2020, 13(15), 3815; https://doi.org/10.3390/en13153815
Submission received: 5 July 2020 / Revised: 21 July 2020 / Accepted: 22 July 2020 / Published: 24 July 2020
(This article belongs to the Special Issue Nanoscale Heat Transfer and Fluid Flow, Multiphase Flows, and CFD Research)
Browse Figures
Versions Notes

Abstract

:
As an unconventional energy source, the development of shale oil plays a positive role in global energy, while shale oil is widespread in organic nanopores. Kerogen is the main organic matter component in shale and affects the flow behaviour in nanoscale-confined spaces. In this work, a molecular dynamic simulation was conducted to study the transport behaviour of shale oil within kerogen nanoslits. The segment fitting method was used to characterise the velocity and flow rate. The heterogeneous density distributions of shale oil and its different components were assessed, and the effects of different driving forces and temperatures on its flow behaviours were examined. Due to the scattering effect of the kerogen wall on high-speed fluid, the heavy components (asphaltene) increased in bulk phase regions, and the light components, such as methane, were concentrated in boundary layers. As the driving force increased, the velocity profile demonstrated plug flow in the bulk regions and a half-parabolic distribution in the boundary layers. Increasing the driving force facilitated the desorption of asphaltene on kerogen walls, but increasing the temperature had a negative impact on the flow velocity.

Graphical Abstract

1. Introduction

The development of shale oil has ameliorated global energy shortages, and many countries have launched programmes to investigate various development approaches [1,2,3]. However, the complex structure of nanopores in shale and the different components in shale oil hinder the further study of shale oil flow behaviours [4,5].
The sizes of pores in shale range from nanometres to micrometres, but experimental nanoscale studies are restricted to laboratory assessments [6,7,8,9,10,11,12]. Molecular dynamic (MD) simulations are often used to study the fluid behaviours within nano-confined spaces [13]. MD simulations are based on Newtonian mechanics and can be used to calculate a system’s thermodynamic quantities and other macroscopic properties. Shale is mainly composed of organic and inorganic matter [14,15,16]. The inorganic matter contains quartz and clay minerals. As a source of oil, kerogen is the main component of organic matter [17]. Thus, the flow behaviour of shale oil in realistic kerogen channels needs to be investigated.
Bousige et al. [18] produced a realistic molecular kerogen model using the generalised phonon densities of states. Ungerer et al. [19] classified kerogen molecules into four types of maturity and constructed corresponding structures. It is difficult for shale oil to flow in a kerogen matrix as a result of kerogen’s dense matrix structure [20], so the reasonable construction of kerogen channels is necessary. During the kerogen matrix generation process, the insertion of repulsive dummy particles can produce porous models [21,22]. Perez et al. [8] blended a fluid mixture with kerogen monomers and simulated the annealing process, and the fluid molecules gathered as clusters. Kerogen monomers form organic frameworks. However, it is difficult to obtain clear transport characteristics in irregular channels. Carbon nanotubes (CNTs) and graphene slits are common flow channel models [7,23], but the flow rate can be overestimated on ultra-smooth surfaces. In multicomponent fluids, heterogeneous density distribution characteristics cannot be produced on smooth surfaces. Due to the driving force’s effect, the velocity profile tends to plug in smooth channels rather than parabolas on rough walls [24]. Thus, constructing flow channels with kerogen is a more reasonable choice.
The flow channel’s boundary condition affects the slip length [25]. Due to the presence of slippage, Darcy’s law is invalid in nanoscale fluid flows [20,26]. The slippage effect can be characterised using the slip length concept, which is defined as the distance between the solid surface and the point where the velocity extrapolation is zero [27]. Martini et al. [27] found, at a low driving force, the movement of only a few molecules along a wall, called a “defect slip” in a nonlinear mode. At a high driving force, all of the fluid molecules adjacent to the liquid–solid interface contribute to “global slip.” Conversely, on a rough kerogen wall, the boundary’s cavity can trap some molecules. In addition, fluid molecules impinge protrusions on the interface, decelerating the velocity in the boundary layer [28,29,30]. However, to the best of our knowledge, very few reports in the literature discuss multicomponent shale oil slippage.
In this study, we constructed a kerogen slit [31,32,33] and used a nonequilibrium molecular dynamic (NEMD) simulation to analyse the flow behaviour of shale oil. We also examined the effects of the driving force and temperature, and the simulation results were fitted using the Poiseuille formula by dividing the channel into two sections. We calculated the flow rate using boundary layers under multicomponent shale oil conditions.

2. Methodology

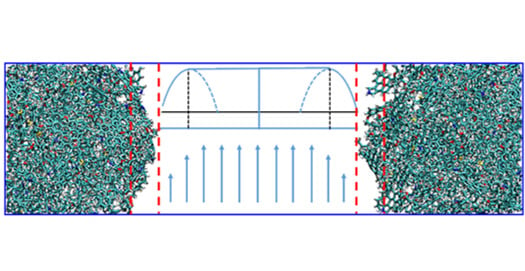
2.1. Molecular Models

In this study, type Ⅱ-C kerogen monomers were used to construct realistic organic slits because the Ⅱ-C kerogen tended to be present in organic-rich shales [19]. We used a simplified shale oil component model including different molecular weight models (C1, C4, C8, C12, methylbenzene, asphaltene) [8,33,34]. The details and structures of the kerogen molecules and shale oil models are provided in the Supporting Information, and the model of the slit system is shown in Figure 1. There were 26,899 atoms in the entire system. The dimensions of the simulation box were 40 Å3 × 50 Å3 × 200 Å3, and each kerogen matrix contained 15 kerogen monomers.
We used a polymer consistent force field (PCFF) for all of the molecules [19,35,36], and described the Van der Waals interactions using Lennard–Jones (LJ) potentials. The parameters between different molecules were calculated using Waldman–Hagler combining rules [37]. The Ewald method was adopted to compute the electrostatic potential [38]. The boundary conditions in three directions were periodic, and the cut-off distance was 12 Å.

2.2. Simulation Methods

The large-scale atomic/molecular massively parallel simulator (LAMMPS) package distributed by Sandia National Laboratories was used for the molecular simulations [39]. The MD simulation in the NVE (The number of atoms, volume and energy of system remain constant.) ensemble was conducted for 50 ps to relax the system’s configuration. The NPT (The number of atoms, pressure and temperature of system remain constant.) ensemble was then performed (P = 30.0 MPa and T = 300 K) for 100 ps. We put the simulation system into the NVT (The number of atoms, volume and temperature of system remain constant.) ensemble at T = 300 K for 200 ps to achieve an equilibrium system. The timesteps of the NVE, NPT, and NVT ensemble simulations were 0.5 fs, 0.5 fs, and 1.0 fs, respectively.
We conducted NEMD simulations with the driving force along the streaming direction. A constant force was applied to each atom rather than a pressure gradient because longitudinally homogeneous pressure can be maintained with a constant field [40]. The NEMD simulations were conducted in the NVT ensemble at 300 K for 18 ns, and we collected the last 6 ns of trajectories for analysis. The temperature was maintained by a Nosé–Hoover thermostat perpendicular to the flow direction [41,42], which reduced the effect of thermal motion on the velocity in the flow direction. During the simulation, as shown in Figure 2, we froze the kerogen matrix layer (KML) and controlled the temperature (300 K) of the rough adsorption layer (RAL) [29,43], which made the kerogen interface flexible [44]. We discussed these layers in the Section 3.1. The free slit layer (FSL) was divided into a bulk phase region and boundary layer, which are discussed in Section 3.3. By averaging the velocity and number of atoms in the bins that were parallel to the flow direction, we obtained the velocity and density profiles [27]. To reduce errors, the simulations were calculated three times independently with the same initial condition.

3. Results and Discussions

3.1. Heterogeneous Density Distribution Analysis

As shown in Figure 2, to more clearly describe the flow behaviour, we divided the system into three regions according to kerogen’s density profile. The KML density fluctuated at 1.1–1.2 g·cm−3 [18,22,32]. The FSL was defined as the free space without kerogen, and the RAL was comprised of the cavities and protrusions of the kerogen between the KML and FSL. The widths of the FSL, RAL, and KML were 5 nm, 1.5 nm, and 2.5 nm, respectively. The roughness of the kerogen matrix’s two walls differed as a result of its amorphous structure, so we only used half of the system to analyse the shale oil fluid’s properties. Due to the random molecular thermal motion effects, there were always slight errors in the shale oil’s distribution. The kerogen wall friction also played a role in the difference between the two halves, but the friction was not our focus.
Using NEMD simulations, we simulated the shale oil flow through the kerogen slit under the driving force’s effect. Figure 3a shows that the shale oil density profile varied considerably at different driving forces. There were two density peaks in the boundary layer at a low driving force, consistent with our previous research [33]. The density profiles presented as a single peak in the middle of the slit at a larger driving force. The difference in the density was small below a driving force of 5 × 10−4 kcal/(mol·Å). Figure 3b shows that the methane density distribution peaked in the RAL region, and the asphaltene’s density peak was distributed in the FSL.
Due to the high flow speed caused by the driving force, the shale oil molecules collided with the kerogen protrusion and had a diffuse scattering behaviour, forming a velocity component perpendicular to the streaming direction [43,45]. The perpendicular velocity component enriched the shale oil in the bulk phase, as shown in Figure 3b, especially in the asphaltene with its complex and large molecular structure. The diffuse scattering reduced the density in the interface [43].
Notably, the density profile remained steady under the different driving forces on the smooth walls [7], and it was difficult to obtain a heterogeneous distribution because the smooth wall could not provide a vertical force from the wall to the fluid. This characteristic was similar to blood flow in the blood vessels; haemoglobin concentrates in the central area and ionic liquid concentrates at the boundary [46,47]. By comparing the results of different driving forces, that the density profiles of asphaltene and methane were opposite, which was important for calculating the flow rate.

3.2. Sensitivity Analysis

3.2.1. Effect of the Driving Force on the Flow Behaviour in the Kerogen Slit

To investigate the driving force’s effects, we conducted the NEMD at driving forces from 15 × 10−4 kcal/(mol·Å) to 40 × 10−4 kcal/(mol·Å). Unlike conventional parabola and plug profiles [36], Figure 4a shows that the velocity distribution was a trapezoid with two arched waists at high driving forces. The heterogeneity of the shale oil caused an interesting flow conformation. According to the previous density analysis, the asphaltene concentrated in the bulk region, while the methane enriched the boundary layer at high driving forces. In this case, as a result of cohesion, the asphaltene formed clusters with a molecular pore network and trapped some small molecules. The linear alkanes sheared easily. The orientation property of the alkanes was observed by solation force experiments [48,49]. However, it was hard to change the configuration of the asphaltene cluster with the shear friction, so the bulk velocity was flat.
In the boundary layer, the methane enrichment made the velocity profile approximately parabolic. Based on the platform and the two halves of the parabolic velocity profile, we divided the FSL into two regions (the bulk phase and boundary layers) and fit the velocity and flow rate [50]. The platform region was the bulk phase (0–12.5 Å), and the halves of the parabola were the boundary layers (12.5–25 Å). Consequently, using the Poiseuille equation, we quantitatively analysed the flow behaviour.
The velocity in the boundary layer increased homogeneously over forces of 30 × 10−4 kcal/(mol·Å), as shown in Figure 4b. By increasing the driving force, the fluid molecules had more kinetic energy, leading to stronger scattering effects. Figure 5 demonstrates that the driving force had a positive effect on the asphaltene density in the bulk phase, and the density profile stabilised beyond 30 × 10−4 kcal/(mol·Å). Due to the strong scattering, the asphaltene density peaks in the RAL were diminished. However, the asphaltene still adsorbed in the RAL and formed density peaks at driving forces below 30 × 10−4 kcal/(mol·Å). Therefore, the constant distribution of the asphaltene density facilitated a steady increase in velocity.

3.2.2. Effect of the Temperature on the Flow Behaviour in the Kerogen Slit

We compared the velocity profiles of the shale oil subjected to different temperatures, as shown in Figure 6a. In general, the fluid had a higher velocity as the temperature increased because the stronger thermal motion facilitated the reduction in viscosity. However, the velocity decreased and the asphaltene’s density profiles were gentler as the temperature increased, as shown in Figure 6.
The higher temperature of the single component fluid reduced its viscosity. In the confined nanoslits, the temperature affected the shale oil’s heterogeneous density distribution. The asphaltene cluster behaved as a complex molecular network. The stronger thermal motion increased the distance between the asphaltene atoms, expanding the asphaltene cluster and increasing its concentration in the boundary layer, as shown in Figure 6b. Thus, the higher temperature weakened the density distribution heterogeneity, and the fluid in the boundary layer was mixed with more asphaltene molecules, increasing the friction between the kerogen and asphaltene. Therefore, the high temperature had a negative effect on the shale oil flow, with asphaltene clusters in the nanochannels.

3.3. Slip Analysis and Fitting

3.3.1. Slip Length Analysis of the Transport Condition

The slip occurred in the nanochannels, which was confirmed by many studies [25,51,52,53]. The slip length was affected by the slip wall location, so we selected the slip boundary at the interface between the FSL and RAL [54]. Because the kerogen protrusion created extra flow resistance in the RAL, destabilising the flow, the flow in the FSL was only affected by the viscosity and driving force.
We calculated the slip length using Ls = usurf/(du/dr), where Ls is the slip length, usurf is the velocity at the slip wall, and du/dr is the velocity gradient at the interface [55]. As shown in Figure 7, the slip length increased steadily over a driving force of 30 × 10−4 kcal/(mol·Å). Below a driving force of 25 × 10−4 kcal/(mol·Å), the slip length increased unstably. Because the asphaltene was still adsorbed at the boundary at low driving forces, the adsorption affected the slip at the boundary.

3.3.2. Segment Fitting on the Flow Behaviour in the Kerogen Slit

Due to the extremely heterogeneous density and velocity, it was difficult to obtain a constant boundary layer viscosity. We attained a linear viscosity distribution by separating the regions and calculating the shear stress and shear velocity, respectively, in the boundary layer using Equations (1)–(4) [56,57],
P ( z ) = F ∫ 0 z n ( z ′ ) d z ′
γ ( z ) = d u d z
η ( z ) = − P ( z ) γ ( z )
where n is the fluid density, z is the distance from the centre of the slit, P is the shear stress, F is the driving force, γ is the shear velocity, u is the velocity, and η is the viscosity. We calculated a series of shale oil density values in parallel bins of 4 × 5 × w b i n nm3 using n ( z i ) = ∑ N i / ( 4 × 5 × w b i n ) , where w b i n is the width of the bins and Ni is the number of atoms in the bins. The viscosity distribution is expressed as
η ( z ) = η ( z a ) − η ( z a ) − η ( z w ) N b i n ⋅ z − a w b i n
where a = w / 2 − b , as shown in Figure 8. a is half of the length of the half-bulk phase layer, b is half of the length of the boundary layer, and w is the slit width. Nbin is the number of bins, η ( z a ) is the viscosity on the border between the bulk phase layer and boundary layer, and η ( z w ) is the viscosity at the interface between the FSL and RAL. We obtained the viscosity distribution in the boundary layer by averaging the difference between η ( z a ) and η ( z w ) as expressed in Equation (4).
The velocity of the Poiseuille flow modified by the slip is expressed in Equation (5) [7],
u ( z ) = − n ( z ) F 2 η ( z ) ( z 2 − w 2 4 − w L s )
where the w is the slit width. The velocity in the boundary layer is expressed in Equation (6).
u 1 ( z ) = − n ( z ) F 2 η ( z ) [ ( z − a ) 2 − b 2 − b L s ]
Equation (7) expresses the velocity of the bulk phase layer where z is equal to a.
u 2 ( z a ) = − n ( z a ) F 2 η ( z a ) ( − b 2 − b L s )
Although the linear distribution of the viscosity cannot perfectly describe the real viscosity, the velocity profile presented in Figure 8 calculated using the NEMD simulations fully fit with Equation (6) and Equation (7).
The FSL flow rate is integrated using Equation (6) and Equation (7), as expressed in Equation (8):
Q = n ( z ) F 2 η ( z ) b 2 ( 2 3 b + L s ) + n ( z a ) F 2 η ( z a ) a b ( b + L s )
Substituting Equation (4) into Equation (8) obtains
Q = F b 2 { N b i n w b i n n ( z ) b ( 2 3 b + L s ) N b i n w b i n η ( z a ) − [ η ( z a ) − η ( z w ) ] ⋅ ( z − a ) + n ( z a ) a ( b + L s ) η ( z a ) }
where Q is the flow rate. Compared with the flow rate using the NEMD simulations, as demonstrated in Equation (10), Figure 9 shows that the separate fitting worked well for the heterogeneous shale oil flow.
Q M D = ∑ z 1 z 2 Δ z · u 1 M D ( z i )
For the different interfaces in the kerogen matrix, we selected half of the system to fit the flow rate. Figure 9 demonstrates that the monotonically increasing flow rate was a result of the increased driving force. However, the different slopes in the flow rate vs. the driving force at 30 × 10−4 kcal/(mol·Å) were an unexpected finding.
As shown in Figure 5, the density peak of the asphaltene in the RAL slowly decreased, suggesting that the asphaltene molecules desorbed from the RAL and flowed into the bulk phase below 30 × 10−4 kcal/(mol·Å). Figure 9 demonstrates that the flow rate increased at a higher rate below the driving force of 30 × 10−4 kcal/(mol·Å), so the stronger driving force facilitated the recovery of asphaltene in the boundary layer.

4. Conclusions

In this work, using MD simulations, we studied the flow behaviour of multicomponent shale oil in realistic kerogen nanoslits. Compared with previous static adsorption results, we found opposite density distributions for asphaltene and methane. The asphaltene increased in the bulk phase layer, while the methane concentrated in the boundary layer. Due to kerogen’s effects, high-velocity asphaltene more easily scattered in the bulk phase. The fast transportation of shale oil demonstrated a different flow behaviour. The asphaltene group was constrained in the bulk phase region and behaved as a plug flow, and the velocity profile in the boundary layer presented as a half of a parabola.
The driving force had a positive effect on the shale oil velocity. The density distribution of asphaltene remained steady beyond the driving force of 30 × 10−4 kcal/(mol·Å), while it showed a slightly denser peak at a smaller driving force. As the temperature increased, due to the stronger thermal motion, the asphaltene’s density distribution was relatively gentle. Thus, the boundary layer viscosity increased and then the velocity decreased in the slit. This characteristic is unusual in macro-flow, but the asphaltene cluster cohesion increased the internal friction of the shale oil in the nano-confined channel.
According to the different velocity profiles in the bulk phase and boundary layer, we employed the Poiseuille equation to fit the velocity and flow rate, respectively. As a result of the asphaltene desorption, the slope of the flow rate maintained a higher value below the driving force of 30 × 10−4 kcal/(mol·Å). Calculating the viscosity of multicomponent shale oil remains challenging, especially in nano channels. This study proposed a new perspective on shale oil transport.

Author Contributions

J.L. did the data curation and wrote the original draft. Y.Y. provided the software and computing resources, and designed the simulation. Y.Z., Q.M. and S.Y. provided general supervision and formal analysis. C.W. analyzed the resulting data and did the validation. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by: the National Natural Science Foundation of China (No. 51674280, 51704033, and 51950410591), Shandong Provincial Natural Science Foundation (ZR2019JQ21), PetroChina Innovation Foundation (No. 2018D-5007-0210), and the Programme for Changjiang Scholars and Innovative Research Teams in University (IRT_16R69).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hughes, J.D. Energy: A reality check on the shale revolution. Nature 2013, 494, 307–308. [Google Scholar] [CrossRef]
  2. Monteiro, P.J.M.; Rycroft, C.H.; Grigory Isaakovich, B. A mathematical model of fluid and gas flow in nanoporous media. Proc. Natl. Acad. Sci. USA 2012, 109, 20309–20313. [Google Scholar] [CrossRef] [Green Version]
  3. Smith, J.F. New Study: “The Shale Oil Boom: A U.S. Phenomenon”; Harvard Kennedy School, Belfer Center for Science and International Affairs: Cambridge, MA, USA, 2013. [Google Scholar]
  4. Kerr, R.A. Natural Gas From Shale Bursts Onto the Scene. Science 2010, 328, 1624–1626. [Google Scholar] [CrossRef] [PubMed]
  5. Wang, Y. Nanogeochemistry: Nanostructures, emergent properties and their control on geochemical reactions and mass transfers. Chem. Geol. 2014, 378–379, 1–23. [Google Scholar] [CrossRef]
  6. Javadpour, F. Nanopores and Apparent Permeability of Gas Flow in Mudrocks (Shales and Siltstone). J. Can. Pet. Technol. 2009, 48, 16–21. [Google Scholar] [CrossRef]
  7. Wang, S.; Javadpour, F.; Feng, Q. Molecular dynamics simulations of oil transport through inorganic nanopores in shale. Fuel 2016, 171, 74–86. [Google Scholar] [CrossRef]
  8. Perez, F.; Devegowda, D. Spatial distribution of reservoir fluids in mature kerogen using molecular simulations. Fuel 2019, 235, 448–459. [Google Scholar] [CrossRef]
  9. Yang, Y.F.; Wang, K.; Zhang, L.; Sun, H.; Zhang, K.; Ma, J.S. Pore-scale simulation of shale oil flow based on pore network model. Fuel 2019, 251, 683–692. [Google Scholar] [CrossRef]
  10. Wang, X.; Yin, H.; Zhao, X.; Li, B.; Yang, Y. Microscopic remaining oil distribution and quantitative analysis of polymer flooding based on CT scanning. Adv. Geo-Energy Res. 2019, 3, 448–456. [Google Scholar] [CrossRef] [Green Version]
  11. Zhou, S.; Ning, Y.; Wang, H.; Liu, H.; Xue, H. Investigation of methane adsorption mechanism on Longmaxi shale by combining the micropore filling and monolayer coverage theories. Adv. Geo-Energy Res. 2018, 2, 269–281. [Google Scholar] [CrossRef] [Green Version]
  12. Cai, J.; Hu, X. Petrophysical Characterization and Fluids Transport in Unconventional Reservoirs; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
  13. Li, Z.; Yao, J.; Ren, Z.; Sun, H.; Zhang, L.; Yang, Y.; Fan, J.; Kou, J. Accumulation behaviors of methane in the aqueous environment with organic matters. Fuel 2019, 236, 836–842. [Google Scholar] [CrossRef]
  14. Song, W.H.; Yao, J.; Li, Y.; Sun, H.; Zhang, L.; Yang, Y.F.; Zhao, J.L.; Sui, H.G. Apparent gas permeability in an organic-rich shale reservoir. Fuel 2016, 181, 973–984. [Google Scholar] [CrossRef]
  15. Wang, S.; Feng, Q.; Farzam, J.; Zha, M.; Cui, R. Multiscale Modeling of Gas Transport in Shale Matrix: An Integrated Study of Molecular Dynamics and Rigid-Pore-Network Model. SPE J. 2020, 25, 1416–1442. [Google Scholar] [CrossRef]
  16. Yang, Y.F.; Yao, J.; Wang, C.C.; Gao, Y.; Zhang, Q.; An, S.Y.; Song, W.H. New pore space characterization method of shale matrix formation by considering organic and inorganic pores. J. Nat. Gas Sci. Eng. 2015, 27, 496–503. [Google Scholar] [CrossRef]
  17. JM, H.; GW, J. Oil and organic matter in source rocks of petroleum. AAPG Bull. 1956, 40, 477–488. [Google Scholar]
  18. Bousige, C.; Ghimbeu, C.M.; Vix-Guterl, C.; Pomerantz, A.E.; Suleimenova, A.; Vaughan, G.; Garbarino, G.; Feygenson, M.; Wildgruber, C.; Ulm, F.J. Realistic molecular model of kerogen’s nanostructure. Nat. Mater. 2016, 15, 576. [Google Scholar] [CrossRef] [PubMed]
  19. Ungerer, P.; Collell, J.; Yiannourakou, M. Molecular Modeling of the Volumetric and Thermodynamic Properties of Kerogen: In fluence of Organic Type and Maturity. Energy Fuels 2015, 29, 91–105. [Google Scholar] [CrossRef]
  20. Obliger, A.; Pellenq, R.; Ulm, F.J.; Coasne, B. Free Volume Theory of Hydrocarbon Mixture Transport in Nanoporous Materials. J. Phys. Chem. Lett. 2017, 7, 3712–3717. [Google Scholar] [CrossRef]
  21. B, Z.; R, X.; P, J. Novel molecular simulation process design of adsorption in realistic shale kerogen spherical pores. Fuel 2016, 180, 718–726. [Google Scholar]
  22. Collell, J.; Galliero, G.; Gouth, F.; Montel, F.; Pujol, M.; Ungerer, P.; Yiannourakou, M. Molecular simulation and modelisation of methane/ethane mixtures adsorption onto a microporous molecular model of kerogen under typical reservoir conditions. Microporous Mesoporous Mater. 2014, 197, 194–203. [Google Scholar] [CrossRef]
  23. Kou, J.; Yao, J.; Lu, H.; Zhang, B.; Li, A.; Sun, Z.; Zhang, J.; Fang, Y.; Wu, F.; Fan, J. Electromanipulating Water Flow in Nanochannels. Nanochannels 2014, 54, 2351–2355. [Google Scholar]
  24. Kerstin, F.; Felix, S.; Laurent, J.; Netz, R.R.; Lydéric, B. Ultralow liquid/solid friction in carbon nanotubes: Comprehensive theory for alcohols, alkanes, OMCTS, and water. Langmuir ACS J. Surf. Colloids 2012, 28, 14261. [Google Scholar]
  25. Li, Y.; Xu, J.; Li, D. Molecular dynamics simulation of nanoscale liquid flows. Microfluid. Nanofluidics 2010, 9, 1011–1031. [Google Scholar] [CrossRef]
  26. Falk, K.; Coasne, B.; Pellenq, R.; Ulm, F.J.; Bocquet, L. Subcontinuum mass transport of condensed hydrocarbons in nanoporous media. Nat. Commun. 2014, 6, 6949. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  27. Martini, A.; Roxin, A.; Snurr, R.Q.; Wang, Q.; Lichter, S. Molecular mechanisms of liquid slip. J. Fluid Mech. 2008, 600, 257–269. [Google Scholar] [CrossRef] [Green Version]
  28. Qiao, R. Effects of molecular level surface roughness on electroosmotic flow. Microfluid. Nanofluidics 2007, 3, 33–38. [Google Scholar] [CrossRef]
  29. Stefano, B.; Todd, B.D.; Searles, D.J. Thermostating highly confined fluids. J. Chem. Phys. 2010, 132, 1016. [Google Scholar]
  30. Arya, G.; Chang, H.C.; Maginn, E.J. Molecular Simulations of Knudsen Wall-slip: Effect of Wall Morphology. Mol. Simul. 2003, 29, 697–709. [Google Scholar] [CrossRef]
  31. Sun, H.; Hui, Z.; Na, Q.; Ying, L. Molecular Insights into the Enhanced Shale Gas Recovery by Carbon Dioxide in Kerogen Slit-Nanopores. J. Phys. Chem. C 2017, 121, 10233–10241. [Google Scholar] [CrossRef]
  32. Tesson, S.; Firoozabadi, A. Methane Adsorption and Self-Diffusion in Shale Kerogen and Slit Nanopores by Molecular Simulations. J. Phys. Chem. C 2018, 122, 23528–23542. [Google Scholar] [CrossRef]
  33. Yang, Y.; Liu, J.; Yao, J.; Kou, J.; Li, Z.; Wu, T.; Zhang, K.; Zhang, L.; Sun, H. Adsorption Behaviors of Shale Oil in Kerogen Slit by Molecular Simulation. Chem. Eng. J. 2020, 387, 124054. [Google Scholar] [CrossRef]
  34. Collell, J.; Ungerer, P.; Galliero, G.; Yiannourakou, M.; Montel, F.; Pujol, M. Molecular Simulation of Bulk Organic Matter in Type II Shales in the Middle of the Oil Formation Window. Energy Fuels 2015, 28, 7457–7466. [Google Scholar] [CrossRef]
  35. Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
  36. Wang, S.; Javadpour, F.; Feng, Q. Fast mass transport of oil and supercritical carbon dioxide through organic nanopores in shale. Fuel 2016, 181, 741–758. [Google Scholar] [CrossRef]
  37. Waldman, M.; Hagler, A.T. New combining rules for rare gas van der Waals parameters. J. Comput. Chem. 1993, 14, 1077–1084. [Google Scholar] [CrossRef]
  38. York, D.M.; Darden, T.A.; Pedersen, L.G. The effect of long-range electrostatic interactions in simulations of macromolecular crystals: A comparison of the Ewald and truncated list methods. J. Chem. Phys. 1993, 99, 8345–8348. [Google Scholar] [CrossRef]
  39. Srinivasan, S.G.; Ashok, I.; Jônsson, H.; Kalonji, G.; Zahorjan, J. Parallel short-range molecular dynamics using the Ādhāra runtime system. Comput. Phys. Commun. 1997, 102, 28–43. [Google Scholar] [CrossRef]
  40. Travis, K.P.; Todd, B.D.; Evans, D.J. Poiseuille flow of molecular fluids. Phys. A-Stat. Mech. Appl. 1997, 240, 315–327. [Google Scholar] [CrossRef]
  41. Sundaram, D.S.; Puri, P.; Yang, V. Thermochemical Behavior of Nickel-Coated Nanoaluminum Particles. J. Phys. Chem. C 2013, 117, 7858–7869. [Google Scholar] [CrossRef]
  42. Nose, S.; Klein, M.L. A study of solid and liquid carbon tetrafluoride using the constant pressure molecular dynamics technique. J.Chem. Phys. 1983, 78, 6928–6939. [Google Scholar] [CrossRef]
  43. Sokhan, V.P.; Nicholson, D.; Quirke, N. Fluid flow in nanopores: An examination of hydrodynamic boundary conditions. J.Chem. Phys. 2001, 115, 3878–3887. [Google Scholar] [CrossRef]
  44. Nagayama, G.; Ping, C. Effects of interface wettability on microscale flow by molecular dynamics simulation. Int. J. Heat Mass Transf. 2004, 47, 501–513. [Google Scholar] [CrossRef]
  45. Peter, D.; Billy, T. Challenges in Nanofluidics—Beyond Navier–Stokes at the Molecular Scale. Processes 2018, 6, 144. [Google Scholar]
  46. Sankar, D.S.; Hemalatha, K. A non-Newtonian fluid flow model for blood flow through a catheterized artery—Steady flow. Appl. Math. Model. 2007, 31, 1847–1864. [Google Scholar] [CrossRef] [Green Version]
  47. Hughes, C.; Lerman, C.; Schwartz, M.; Peshkin, B.N.; Wenzel, L.; Narod, S.; Corio, C.; Tercyak, K.P.; Hanna, D.; Isaacs, C. Effects of couple-stresses on the dispersion of a soluble matter in a pipe flow of blood. Rheol. Acta 1980, 19, 710–715. [Google Scholar]
  48. Zheng, Y.; Li, Q.; Rui, H.; Gray, M.R.; Chou, K.C. Competitive Adsorption of Toluene and n-Alkanes at Binary Solution/Silica Interfaces. J. Phys. Chem. C 2009, 113, 20355–20359. [Google Scholar]
  49. Christenson, H.K.; Gruen, D.W.R.; Horn, R.G.; Israelachvili, J.N. Structuring in liquid alkanes between solid surfaces: Force measurements and mean-field theory. Cheminform 1987, 87, 1834–1841. [Google Scholar]
  50. Chaturani, P.; Upadhya, V.S. A two-fluid model for blood flow through small diameter tubes. Biorheology 1979, 16, 109–118. [Google Scholar] [CrossRef]
  51. Niavarani, A.; Priezjev, N.V. Rheological study of polymer flow past rough surfaces with slip boundary conditions. J. Chem. Phys. 2008, 129, 425. [Google Scholar] [CrossRef] [Green Version]
  52. Niavarani, A.; Priezjev, N.V. Slip boundary conditions for shear flow of polymer melts past atomically flat surfaces. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2008, 77, 041606. [Google Scholar] [CrossRef] [Green Version]
  53. Holt, J.K.; Hyung Gyu, P.; Yinmin, W.; Michael, S.; Artyukhin, A.B.; Grigoropoulos, C.P.; Aleksandr, N.; Olgica, B. Fast mass transport through sub-2-nanometer carbon nanotubes. Science 2006, 312, 1034–1037. [Google Scholar] [CrossRef] [PubMed]
  54. BoţAn, A.; Rotenberg, B.; Marry, V.; Turq, P.; Noetinger, B.T. Hydrodynamics in Clay Nanopores. J. Phys. Chem. C 2011, 115, 16109–16115. [Google Scholar] [CrossRef]
  55. Wua, K.; Chena, Z.; Lib, J.; Lib, X.; Xua, J.; Dong, X. Wettability effect on nanoconfined water flow. PNAS 2017, 114, 3358–3363. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  56. Předota, M.; Cummings, P.T.; Wesolowski, D.J. Electric Double Layer at the Rutile (110) Surface. 3. Inhomogeneous Viscosity and Diffusivity Measurement by Computer Simulations. J. Phys. Chem. C 2007, 111, 3071–3079. [Google Scholar] [CrossRef]
  57. Bitsanis, I.; Vanderlick, T.K.; Tirrell, M.; Davis, H.T. A Tractable Molecular Theory of Flow in Strongly Inhomogeneous Fluids. J. Chem. Phys. 1988, 89, 3152–3162. [Google Scholar] [CrossRef]
Energies 13 03815 g001 550
Figure 1. Molecular model of the kerogen slits constructed with a kerogen matrix and multicomponent shale oil. Molecular colours: red, kerogen; black, asphaltene; grey, methylbenzene; purple, n-dodecane; mauve, n-octane; pink, n-butane; green, propane; yellow, ethane; blue, methane.
Figure 1. Molecular model of the kerogen slits constructed with a kerogen matrix and multicomponent shale oil. Molecular colours: red, kerogen; black, asphaltene; grey, methylbenzene; purple, n-dodecane; mauve, n-octane; pink, n-butane; green, propane; yellow, ethane; blue, methane.
Energies 13 03815 g001
Energies 13 03815 g002 550
Figure 2. The density profile of kerogen. The dashed line segments represent the kerogen matrix layer (KML), rough adsorption layer (RAL), and free slit layer (FSL) systems.
Figure 2. The density profile of kerogen. The dashed line segments represent the kerogen matrix layer (KML), rough adsorption layer (RAL), and free slit layer (FSL) systems.
Energies 13 03815 g002
Energies 13 03815 g003 550
Figure 3. NEMD simulations: (a) The density profile of the fluid at different driving forces. (b) The density profile of the shale oil’s components assessed by the NEMD simulations. F = 40 × 10−4 kcal/(mol·Å). T = 300 K.
Figure 3. NEMD simulations: (a) The density profile of the fluid at different driving forces. (b) The density profile of the shale oil’s components assessed by the NEMD simulations. F = 40 × 10−4 kcal/(mol·Å). T = 300 K.
Energies 13 03815 g003
Energies 13 03815 g004 550
Figure 4. Velocity profiles: (a) The velocity profile of the shale oil at different driving forces. (b) The velocity profile in the boundary layer. T = 300 K.
Figure 4. Velocity profiles: (a) The velocity profile of the shale oil at different driving forces. (b) The velocity profile in the boundary layer. T = 300 K.
Energies 13 03815 g004
Energies 13 03815 g005 550
Figure 5. The density profile of the asphaltene at different driving forces. T = 300 K. The dashed blue lines are the borders of the KML, RAL, and FSL.
Figure 5. The density profile of the asphaltene at different driving forces. T = 300 K. The dashed blue lines are the borders of the KML, RAL, and FSL.
Energies 13 03815 g005
Energies 13 03815 g006 550
Figure 6. Effect of the Temperature: (a) The fluid velocity profiles at different temperatures. (b) The asphaltene’s density at different temperatures. F = 30 × 10-4 kcal/(mol·Å).
Figure 6. Effect of the Temperature: (a) The fluid velocity profiles at different temperatures. (b) The asphaltene’s density at different temperatures. F = 30 × 10-4 kcal/(mol·Å).
Energies 13 03815 g006
Energies 13 03815 g007 550
Figure 7. The slip length at different driving forces. T = 300 K.
Figure 7. The slip length at different driving forces. T = 300 K.
Energies 13 03815 g007
Energies 13 03815 g008 550
Figure 8. The separate fitting of the fluid velocity profile. F = 30 × 10−4 kcal/mol. (The dashed red line is the fitting in the free layer with the same velocity where z = 12.5Å. The dashed blue line is the separation between the boundary and bulk phase layers. Half of the velocity profile is in the FSL).
Figure 8. The separate fitting of the fluid velocity profile. F = 30 × 10−4 kcal/mol. (The dashed red line is the fitting in the free layer with the same velocity where z = 12.5Å. The dashed blue line is the separation between the boundary and bulk phase layers. Half of the velocity profile is in the FSL).
Energies 13 03815 g008
Energies 13 03815 g009 550
Figure 9. The segmentation fitting of the fluid flow rate (half of the fluid) at different driving forces. T = 300 K. Some error bars are smaller than the scatter size.
Figure 9. The segmentation fitting of the fluid flow rate (half of the fluid) at different driving forces. T = 300 K. Some error bars are smaller than the scatter size.
Energies 13 03815 g009

Share and Cite

MDPI and ACS Style

Liu, J.; Zhao, Y.; Yang, Y.; Mei, Q.; Yang, S.; Wang, C. Multicomponent Shale Oil Flow in Real Kerogen Structures via Molecular Dynamic Simulation. Energies 2020, 13, 3815. https://doi.org/10.3390/en13153815

AMA Style

Liu J, Zhao Y, Yang Y, Mei Q, Yang S, Wang C. Multicomponent Shale Oil Flow in Real Kerogen Structures via Molecular Dynamic Simulation. Energies. 2020; 13(15):3815. https://doi.org/10.3390/en13153815

Chicago/Turabian Style

Liu, Jie, Yi Zhao, Yongfei Yang, Qingyan Mei, Shan Yang, and Chenchen Wang. 2020. "Multicomponent Shale Oil Flow in Real Kerogen Structures via Molecular Dynamic Simulation" Energies 13, no. 15: 3815. https://doi.org/10.3390/en13153815

APA Style

Liu, J., Zhao, Y., Yang, Y., Mei, Q., Yang, S., & Wang, C. (2020). Multicomponent Shale Oil Flow in Real Kerogen Structures via Molecular Dynamic Simulation. Energies, 13(15), 3815. https://doi.org/10.3390/en13153815

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop