Assessment of Energy Storage from Photovoltaic Installations in Poland Using Batteries or Hydrogen
Abstract
:1. Introduction
2. Materials and Methods
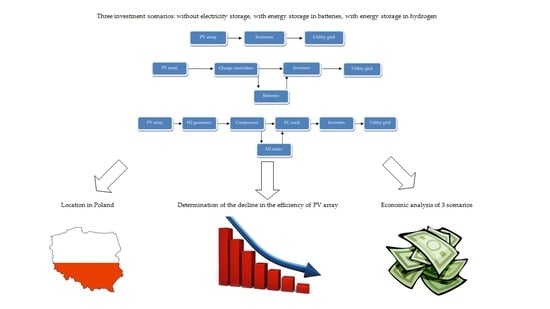
- Scenario 1. The energy produced from the PV system without storage (reference scenario). The price is set up on the RES auctions and the average price of sold energy (Figure 1a);
- Scenario 2. Energy from the PV system is stored with batteries and sold at the price of the afternoon peak (Figure 1b);
- Scenario 3. Energy from PV is stored and sold at the price of the afternoon peak as well, but the storage bases on hydrogen, electrolyzer and PEM fuel cell stack (Figure 1c).
- (1)
- evaluation of solar potential in Poland and the place designated for the investment especially, based on meteorological data and performed by simulation using the Krieg estimation method; the determination of the decrease in actual installation capacity over the years,
- (2)
- design of the installation and investment cost analysis for investigated scenarios,
- (3)
- economic assessment taking into account the simulated energy production, actual energy prices, discount rate, and economic indexes.
2.1. Solar Potential in Poland
2.2. Estimation of the Energy Production Reduction
2.3. Assumptions for Technical and Economic Analysis
- (1)
- the nominal power of PV farm Pinst = 100 kW,
- (2)
- the location of the solar farm-Poland, Wroclaw, Lower Silesia (51°08’ N; 17°07′ E),
- (3)
- the PV farm is located close to the medium voltage network with free capacity,
- (4)
- the type of the montage system: free-standing installation based on piles driven into the ground,
- (5)
- the main components of PV installation: Panel Q.PLUS BFR-G4.1 (PPV = 275 W), inverters SMA Sunny Tripower 9000TL,
- (6)
- the price per hectare of land amounting to 7000 € was accepted [25],
- (7)
- the electricity price was adopted depending on analysis scenario: 80 €·MWh−1 for an array without energy storage, 120 €·MWh−1 for systems with energy storage (price in the afternoon peak) [26],
- (8)
- the PV system O&M costs of 18 €·kW−1·yr−1 were assumed [27],
- (9)
- the connection of the batteries is parallel,
- (10)
- the discount rate r = 2.68% was assumed based on the internal banking index,
- (11)
- the energy accumulation options: energy storage in lithium-ion batteries (Scenario 2), in hydrogen based on the use of an electrolyzer, compressor, cylindrical tank made of kevlar, and fuel cell stack (Scenario 3),
- (12)
2.4. Energy Production by Photovoltaic Installation
2.5. Calculation of the Energy Storage Systems
2.6. Methods of Investment Project Assessment
2.6.1. Simple Payback Period (SPBP)
2.6.2. Return on Investment (ROI)
2.6.3. Net Present Value (NPV)
2.6.4. Internal Return Rate (IRR)
2.6.5. Discounted Payback Period (DPP)
3. Results and Discussion
3.1. Solar Potential at Optimal Angle for Poland
3.2. Technical Calculations
- (1)
- Scenario 2: required battery capacity;
- (2)
- Scenario 3: daily amount of electricity after passing through the electrolyzer, daily amount of energy needed to compress hydrogen to 30 MPa, daily amount of energy for storage, tank volume for hydrogen compressed to = 30 MPa, required fuel cell stack power, daily stored energy for sale after passing through the electrolyzer, compressor and fuel cell stack.
3.3. Results of Measurements of PV Aging
3.4. Results of Economic Analysis of Investment Scenarios
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- CSO of Poland. CSO Energy Statistics in 2017 and 2018; Central Statistical Office of Poland: Warsaw, Poland, 2019.
- EU Parliament and Council. Directive (EU) 2018/2001 of the European Parliament and of the Council of 11 December 2018 on the promotion of the use of energy from renewable sources. Off. J. Eur. Union 2018, 21, 82–209. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX%3A32018L2001 (accessed on 3 August 2020).
- Ministry of Economy of Poland. Announcement of Ministry of Economy from 21.12.2009 in a Matter of the National Energy Policy up to 2030; Monitor of Poland of 2010: Warsaw, Poland, 2009. [Google Scholar]
- Kadar, P. Pros and Cons of the renewable energy application. Acta Polytech. Hung. 2014, 11, 211–224. [Google Scholar]
- Lazzeroni, P.; Moretti, F.; Stirano, F. Economic potential of PV for Italian residential end-users. Energy 2020, 200, 117508. [Google Scholar] [CrossRef]
- Quansah, D.A.; Adaramola, M.S. Ageing and degradation in solar photovoltaic modules installed in northern Ghana. Sol. Energy 2018, 173, 834–847. [Google Scholar] [CrossRef]
- Ferrara, C.; Philipp, D. Why do PV modules fail? Energy Procedia 2012, 15, 379–387. [Google Scholar] [CrossRef]
- Bandou, F.; Arab, A.H.; Belkaid, M.S.; Logerais, P.O.; Riou, O.; Charki, A. Evaluation performance of photovoltaic modules after a long-time operation in Saharan environment. Int. J. Hydrog. Energy 2015, 40, 13839–13848. [Google Scholar] [CrossRef]
- Wohlgemuth, J.H.; Kurtz, S. Using accelerated testing to predict module reliability. In Proceedings of the 37th IEEE Photovoltaic Specialists Conference (PVSC 37), Seattle, Washington, DC, USA, 19–24 June 2011; pp. 1–5. [Google Scholar]
- Jordan, D.C.; Kurtz, S.R. Photovoltaic degradation rates-an analytical review: Photovoltaic degradation rates progress. Photovolt. Res. Appl. 2013, 21, 12–29. [Google Scholar] [CrossRef] [Green Version]
- Meydbray, J.; Dross, F. PV Module Reliability Scorecard Report; DNV GL: Oslo, Norway, 2016. [Google Scholar]
- Reis, A.M.; Coleman, N.T.; Marshall, M.W.; Lehman, P.A.; Chamberlin, C.E. Comparison of PV module performance before and after 11-years of field exposure. In Proceedings of the 29th PV Specialists Conference, New Orleans, LA, USA, 19–24 May 2002; pp. 1432–1435. [Google Scholar] [CrossRef]
- Osterwald, C.R.; Anderberg, A.; Rummel, S.; Ottoson, L. Degradation analysis of weathered crystalline-silicon PV modules. In Proceedings of the 29th PV Specialists Conference, New Orleans, LA, USA, 19–24 May 2002; pp. 1392–1395. [Google Scholar] [CrossRef]
- Belu, R. Energy storage for electric grid and renewable energy application. In Energy Storage, Grid Integration, Energy Economics, and the Environment; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2019; pp. 29–33. [Google Scholar]
- Wojciechowski, H. Technologie magazynowania energii cz. II. Instal 2017, 3, 16–27. [Google Scholar]
- Zuttel, A. Hydrogen storage methods. Naturwissenschaften 2004, 91, 157–172. [Google Scholar] [CrossRef] [PubMed]
- Kharel, S.; Shabani, B. Hydrogen as a long-term large-scale energy storage solution to support renewables. Energies 2018, 11, 2825. [Google Scholar] [CrossRef] [Green Version]
- Dawood, F.; Shafiullah, G.; Anda, M. Stand-Alone microgrid with 100% renewable energy: A case study with hybrid solar PV-battery-hydrogen. Sustainability 2020, 12, 2047. [Google Scholar] [CrossRef] [Green Version]
- International Renewable Energy Agency (IRENA). Hydrogen: A renewable energy perspective. In Proceedings of the 2nd Hydrogen Energy Ministerial Meeting, Tokyo, Japan, 25 September 2019. [Google Scholar]
- Bartosik, M. Magazynowanie energii elektrycznej i gospodarka wodorowa. Przegląd Elektrotechniczny 2016, 1, 334–342. [Google Scholar] [CrossRef]
- Jamrozik, A.; Głuszek, A.; Olejnik, A. Modern methods of energy storage. J. Civ. Eng. Environ. Archit. 2014, 61, 227–236. [Google Scholar] [CrossRef]
- Zhang, Y.; Lundblad, A.; Campana, P.E.; Yan, J. Comparative study of battery storage and hydrogen storage to increase photovoltaic self-sufficiency in a residential building of Sweden. Energy Procedia 2016, 103, 268–273. [Google Scholar] [CrossRef]
- Rakowski, J. Rynek bilansujący energii elektrycznej w Polsce—Geneza, zasady funkcjonowania, przyszłość. Biuletyn Miesięczny. PSE SA 2000, 3, 30. [Google Scholar]
- Niedoba, T. Application of kriging in approximations of grained materials characteristics distribution functions. In Proceedings of the XXV International Mineral Processing Congress, Brisbane, Australia, 6–10 September 2010; pp. 3321–3326. [Google Scholar]
- Sikorska, A. Rynek Ziemi Rolniczej. Analizy rynkowe 2018, 21, 79–80. [Google Scholar]
- Electricity Distributor TAURON. Tariff for Customers of Tariff Groups G11, G12, G12w, G13. Available online: https://www.tauron-dystrybucja.pl/ (accessed on 3 August 2020).
- NREL. Report Distributed Generation Renewable Energy Estimate of Costs; National Renewable Energy Laboratory: Golden, CO, USA, 2016.
- Laronde, R.; Charki, A.; Bigaud, D. Lifetime estimation of a photovoltaic module based on temperature measurement. In Proceedings of the 2nd IMEKO TC 11 International Symposium Metrological Infrastructure, Cavtat, Croatia, 15–17 June 2011. [Google Scholar]
- Sangwongwanich, A.; Yang, Y.; Sera, D.; Blaabjerg, F. Lifetime evaluation of PV inverters considering panel degradation rates and installation sites. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 2845–2852. [Google Scholar] [CrossRef]
- Haidl, B.; Bader, S. Lifetime analysis of energy storage systems for sustainable transportation. Sustainability 2019, 11, 6731. [Google Scholar] [CrossRef] [Green Version]
- Bareiß, K.; de la Rua, C.; Möckl, M.; Hamacher, T. Life cycle assessment of hydrogen from proton exchange membrane water electrolysis in future energy systems. Appl. Energy 2019, 237, 862–872. [Google Scholar] [CrossRef]
- Ramsden, T. An Evaluation of the Total Cost of Ownership of Fuel Cell-Powered Material Handling Equipment; NREL Technical Report: Golden, CO, USA, 2013. [Google Scholar]
- Datasheet of Q. PLUS BFR-G4.1 Solar Panel. Available online: https://archiwum.allegro.pl/oferta/panel-fotowoltaiczny-qcells-qplus-bfr-g4-1-275-285-i7898262517.html (accessed on 3 July 2020).
- Datasheet of SMA Sunny Tripower 9000tl Solar Inverter. Available online: https://www.solar-go.co.uk/sm.a-sunny-tripower-9000tl-20-solar-inverter.html (accessed on 3 July 2020).
- NACAA. NACAA’s Menu of Options Implementing EPA’s Clean Power Plan: A Menu of Options; National Association of Clean Air Agencies: Washington, DC, USA, 2015. [Google Scholar]
- Makibar, A.; Narvarte, L. Characterization and efficiency test of a Li-Ion energy storage system for PV systems. In Proceedings of the 31st European Photovoltaic Solar Energy Conference and Exhibition, Hamburg, Germany, 14–18 September 2015; pp. 1652–1658. [Google Scholar]
- Datasheet of Lithium Battery Tesvolt TS-System 48V. Available online: https://www.solaryours.com/produ.cts/lithium-storage-system-ts-the-commercial-all-rounder/ (accessed on 3 July 2020).
- Wanjiku, J.G.; Khan, M.A.; Barendse, P.S.; Sebitosi, A.B. Analytical sizing of an electrolyser for a small-scale wind electrolysis plant. In Proceedings of the 2010 IEEE International Energy Conference, Manama, Bahrain, 18–22 December 2010. [Google Scholar]
- Dale, N.V.; Mann, M.D.; Salehfar, H.; Han, T.; Dhirde, A.M. Modeling and analysis of electrochemical hydrogen compression. In Proceedings of the NHA Annual Hydrogen Conference, Sacramento Convention Center, Sacramento, CA, USA, 30 March–3 April 2008. [Google Scholar]
- Kaytara, S.; Iżykowski, J.; Staszewski, Ł.; Shaikh, F. Technical and economical evaluation of proton exchange membrane (PEM) fuel cell for commercial applications. Present Probl. Power Syst. Control. 2017, 8, 41–49. [Google Scholar]
- Basinska, M.; Koczyk, H.; Kosmowski, A. Assessment of thermo modernization using the global cost method. Energy Procedia 2015, 78, 2040–2045. [Google Scholar] [CrossRef] [Green Version]
- Zamfir, M.; Manea, M.D.; Ionescu, L. Return on investment—Indicator for measuring the profitability of invested capital. Valahian J. Econ. Stud. 2016, 7, 79–86. [Google Scholar] [CrossRef] [Green Version]
- Wunder, T. What is strategy? In Essentials of Strategic Management: Effective Formulation and Execution of Strategy; Schäffer-Poeschel Verlag: Stuttgart, Germany, 2016; pp. 1–38. [Google Scholar]
- Zizlavsky, O. Net present value approach: Method for economic assessment of innovation projects. Procedia Soc. Behav. Sci. 2014, 156, 506–512. [Google Scholar] [CrossRef]
- El Tahir, Y.; El Otaibi, D. Internal rate of return: A suggested alternative formula and its macro-economic implications. J. Am. Sci. 2014, 10, 216–221. [Google Scholar]
- Bhandari, S.B. Discounted payback period—A viable complement to net present value for projects with conventional cash flows. J. Cost Anal. 1989, 7, 43–53. [Google Scholar] [CrossRef]
- Photovoltaic Geographical Information System (PVGIS). Available online: https://ec.europa.eu/jrc/en/pvgis (accessed on 5 July 2020).
- Quirós, E.; Pozo, M.; Ceballos, J. Solar potential of rooftops in Cáceres city, Spain. J. Maps 2018, 14, 44–51. [Google Scholar] [CrossRef]
- Datasheet of Solar Charge Controller Smart Solar MPPT 100/20 48V. Available online: https://www.inutec-i nt.com/us/victron-energy-smartsolar-mppt-100-20-48v html (accessed on 3 July 2020).
- Ruth, M.; Mayyas, A.; Mann, M. Manufacturing competitiveness analysis for PEM and alkaline water electrolysis systems. In Proceedings of the 2017 Fuel Cell Seminar and Energy Expo, Long Beach Conferation Center, Long Beach, CA, USA, 5–7 September 2017. [Google Scholar]
- Zachmann, G.; Holtermann, M.; Radeke, J.; Tam, M.; Huberty, M.; Naumenko, D.; Faye, A.N. Rationale for supporting the transition to a new energy and transport system. In The Great Transformation: Decarbonising Europe’s Energy and Transport Systems; Bruegel Blueprint: Brussel, Belgium, 2012; Volume 16, pp. 6–38. [Google Scholar]
- Datasheet of Hydrogen Compressor. Available online: https://www.alibaba.com/product-detail/Small-hydrogen--R134A-CAR-REFRIGERATOR-compressor_60424079045.html?spm=a2700.7724857.normalList.212.2 (accessed on 3 July 2020).
- Datasheet of Hydrogen Tank. Available online: https://www.alibaba.com/product-detail/300bar-hydrogen-hydrogen-40L-gas-cylinder-air_60843543250.html?spm=a2700.7724857.normalList.89.2dee3f1ctnzKSW (accessed on 3 July 2020).







| Voivodeship | Voivodeship Capital | Angle, ° |
|---|---|---|
| Lower Silesia | Wroclaw | 36 |
| Kuyavia-Pomerania | Bydgoszcz | 37 |
| Lublin | Lublin | 35 |
| Lubusz | Gorzow Wlkp. | 37 |
| Lodzkie | Lodz | 36 |
| Lesser Poland | Cracow | 35 |
| Masovia | Warsaw | 36 |
| Opole | Opole | 36 |
| Subcarpathia | Rzeszow | 35 |
| Podlasie | Bialystok | 35 |
| Pomerania | Gdansk | 39 |
| Silesia | Katowice | 35 |
| Holy Cross | Kielce | 35 |
| Warmia-Masuria | Olsztyn | 38 |
| Greater Poland | Poznan | 37 |
| West Pomerania | Szczecin | 38 |
| Voivodeship | Voivodeship Capital | Horizontal | Hopt |
|---|---|---|---|
| kWh∙m−2∙yr−1 | kWh∙m−2∙yr−1 | ||
| Lower Silesia | Wroclaw | 1109.022 | 1281.485 |
| Kuyavia-Pomerania | Bydgoszcz | 1080.4 | 1259.25 |
| Lublin | Lublin | 1109.6 | 1266.55 |
| Lubusz | Gorzow Wlkp. | 1091.35 | 1270.2 |
| Lodzkie | Lodz | 1091.35 | 1251.95 |
| Lesser Poland | Cracow | 1102.3 | 1259.25 |
| Masovia | Warsaw | 1080.4 | 1241 |
| Opole | Opole | 1116.9 | 1284.8 |
| Subcarpathia | Rzeszow | 1109.6 | 1270.2 |
| Podlasie | Bialystok | 1062.15 | 1215.45 |
| Pomerania | Gdansk | 1120.55 | 1332.25 |
| Silesia | Katowice | 1098.65 | 1255.6 |
| Holy Cross | Kielce | 1098.65 | 1251.95 |
| Warmia-Masuria | Olsztyn | 1084.05 | 1262.9 |
| Greater Poland | Poznan | 1098.65 | 1273.85 |
| West Pomerania | Szczecin | 1076.75 | 1259.25 |
| Parameter | Scenario 1 | Scenario 2 | Scenario 3 |
|---|---|---|---|
| 0.1626 | 0.1626 | 0.1626 | |
| , pc | 364 | 364 | 364 |
| , kWh∙yr−1 | 113,770 | 113,770 | 113,770 |
| , kWh∙d−1 | 311.7 | 311.7 | 311.7 |
| , Ah | - | 6408 | - |
| , kWh∙d−1 | - | - | 280.53 |
| Nm3∙d−1 | - | - | 22.09 |
| kWh∙d−1 | - | - | 14.18 |
| kWh∙d−1 | - | - | 266.34 |
| , m3 | - | - | 0.252 |
| kW | - | - | 56.7 |
| kWh∙d−1 | - | - | 186.44 |
| Item | Unit | Amount | Unit Price, € | Cost, € |
|---|---|---|---|---|
| PV panel 0.275 kW | pc. | 364 | 128 | 46,592 |
| Land for construction | ha | 0.3 | 7000 | 2100 |
| Inverter 9 kW | pc. | 9 | 1420 | 12,780 |
| Total | - | - | - | 61,472 |
| Item | Unit | Amount | Unit Price, € | Cost, € |
|---|---|---|---|---|
| PV panel 0.275kW | pc. | 364 | 128 | 46,592 |
| Land for construction | ha | 0.3 | 7000 | 2100 |
| Inverter 9kW | pc. | 9 | 1420 | 12,780 |
| Li-Ion battery 940Ah | pc. | 7 | 27,000 | 189,000 |
| Charge regulator | pc. | 7 | 144 | 1152 |
| Total | - | - | - | 251,624 |
| Item | Unit | Amount | Unit Price, € | Cost, € |
|---|---|---|---|---|
| PV panels 0.275 kW | pc. | 364 | 128 | 46,592 |
| Land for construction | ha | 0.3 | 7000 | 2100 |
| Inverter 9 kW | pc. | 9 | 1420 | 12,780 |
| Electrolyzer | pc. | 1 | 1805 | 1805 |
| Compressor | pc | 1 | 225 | 225 |
| Hydrogen tank 0.04 cbm | pc. | 7 | 465 | 3255 |
| Fuel cell stack 63 kW | pc. | 1 | 3087 | 3087 |
| Total | - | - | - | 69,844 |
| No | Description | Unit | No Storage (Scenario 1) | With Batteries (Scenario 2) | With Storage in H2 (Scenario 3) |
|---|---|---|---|---|---|
| 1 | Annual electricity produced | kWh·yr−1 | 104,405 | 104,405 | 104,405 |
| 2 | Annual net electricity stored | kWh·yr−1 | 104,405 | 99,184 | 62,449 |
| 3 | Investment outlays | € | 61,472 | 251,624 | 69,844 |
| 4 | Average annual incomes | €·yr−1 | 8255 | 11,764 | 7407 |
| Scenario | No Storage (Scenario 1) | Batteries (Scenario 2) | Hydrogen Storage (Scenario 3) |
|---|---|---|---|
| Investment expenditures, € | 61,472 | 251,624 | 69,844 |
| Annual profits (average in 30 years), € | 8,255 | 11,764 | 7,407 |
| Annual O&M costs, € | 1800 | 1800 | 1,800 |
| SPBP, years | 8.8 | never | 14.74 |
| ROI (30 years), % | 73.45 | 66.48 | 92.48 |
| NPV (30 years), € | 54,896 | 183,428 | 22,639 |
| IRR (30 years), % | 9.34 | - | 5.28 |
| DPP, years | 10.21 | never | 17.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Knutel, B.; Pierzyńska, A.; Dębowski, M.; Bukowski, P.; Dyjakon, A. Assessment of Energy Storage from Photovoltaic Installations in Poland Using Batteries or Hydrogen. Energies 2020, 13, 4023. https://doi.org/10.3390/en13154023
Knutel B, Pierzyńska A, Dębowski M, Bukowski P, Dyjakon A. Assessment of Energy Storage from Photovoltaic Installations in Poland Using Batteries or Hydrogen. Energies. 2020; 13(15):4023. https://doi.org/10.3390/en13154023
Chicago/Turabian StyleKnutel, Bernard, Anna Pierzyńska, Marcin Dębowski, Przemysław Bukowski, and Arkadiusz Dyjakon. 2020. "Assessment of Energy Storage from Photovoltaic Installations in Poland Using Batteries or Hydrogen" Energies 13, no. 15: 4023. https://doi.org/10.3390/en13154023
APA StyleKnutel, B., Pierzyńska, A., Dębowski, M., Bukowski, P., & Dyjakon, A. (2020). Assessment of Energy Storage from Photovoltaic Installations in Poland Using Batteries or Hydrogen. Energies, 13(15), 4023. https://doi.org/10.3390/en13154023