RANS Simulation of the Effect of Pulse Form on Fluid Flow and Convective Heat Transfer in an Intermittent Round Jet Impingement
Abstract
:1. Introduction
2. Mathematical Model and Numerical Realization
3. Numerical Results and Its Discussion
3.1. Fluid Flow Characteristics
3.2. Heat Transfer
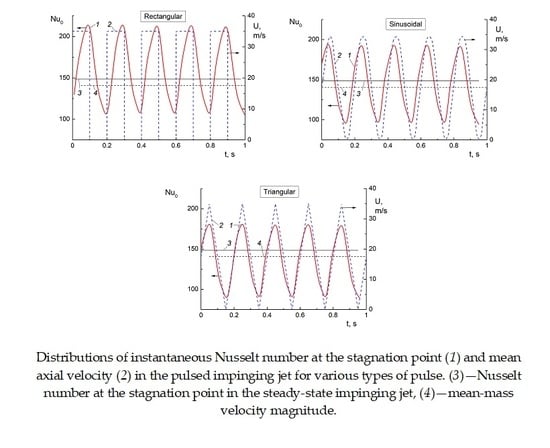
4. Comparison with the Experimental Results in the Pulsed Impinging Jet
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| CP | specific heat capacity, (J kg−1 K−1) |
| D | pipe I.D., (m) |
| DC | DC = ton/(ton+ toff) duty cycle |
| ER | heat transfer enhancement ratio |
| f | frequency of pulsation, (Hz) |
| H/D | normalized distance between pipe outlet and impinging flat plate |
| k | turbulent kinetic energy, (m2 s−2) |
| Nu | Nu = αD/λ Nusselt number |
| P | pressure, (Pa) |
| Pr | Pr =μCP/ λ Prandl number |
| specific gas constant, (J kg−1 K−1) | |
| Re | DUm1/ν Reynolds number |
| r | radial coordinate, (m) |
| St | St = fD/Um1 Strouhal number, based on pipe diameter |
| T | temperature, (K) |
| t | time, (s) |
| ton | flow-on time (the time of open state), (s) |
| toff | flow-off time (the time of closed state), (s) |
| Ui | axial and radial mean velocity components, (m s−1) |
| Um1 | mean-mass velocity in the initial cross-section, (m s−1) |
| U* | friction velocity, obtained for the flow in the pipe, (m s−1) |
| , | r.m.s. velocity fluctuation in axial and radial directions, (m2 s−2) |
| turbulent heat flux, (m K s−1) | |
| Reynolds stress, (m2 s−2) | |
| W | slot width (m) |
| x | axial coordinate, (m) |
| x/H | distance between the pipe outlet and impinging surface |
| y | distance normal to the wall, (m) |
| Greek letters | |
| α | heat transfer coefficient, (W m−2) |
| ε | dissipation of the turbulent kinetic energy, (m2 s−3) |
| λ | heat conductivity, (W K−1 m−1) |
| μ | dynamic viscosity, (kg m−1 s−1) |
| ν | kinematic viscosity, (m2 s−1) |
| ρ | density, (kg m−3) |
| Subscripts | |
| 0 | stagnation point |
| 1 | initial conditions |
| p | pulsed (non-steady-state impinging jet) |
| T | turbulent |
| W | wall |
| m | mean-mass |
| st | steady-state impinging jet |
Acronym
| HTER | heat transfer enhancement ratio |
| RANS | Reynolds averaged Navier-Stokes |
| RMS | root-mean-squire |
References
- Dyban, E.P.; Mazur, A.I. Convective Heat Transfer in Jet Flows around Bodies; Naukova Dumkova: Kiev, Ukraine, 1982. (In Russian) [Google Scholar]
- Mujumdar, A.S. Impingement drying. In Handbook of Industrial Drying, 3rd ed.; Mujumdar, A.S., Ed.; Taylor & Francis Group: New York, NY, USA, 2007; pp. 385–395. [Google Scholar]
- Martin, H. Heat and mass transfer between impinging gas jets and solid surface. Adv. Heat Transf. 1977, 13, 1–60. [Google Scholar]
- Jambunathan, K.; Lai, E.; Moss, M.A.; Button, B.L. A review of heat transfer data for single circular jet impingement. Int. J. Heat Fluid Flow 1992, 13, 106–115. [Google Scholar]
- Viskanta, R. Heat transfer to impinging isothermal gas and flame jets. Int. J. Exp. Therm. Fluid Sci. 1993, 6, 111–134. [Google Scholar]
- Webb, B.W.; Ma, C.F. Single-phase liquid jet impingement heat transfer. Adv. Heat Transfer. 1995, 26, 105–217. [Google Scholar]
- Zuckerman, N.; Lior, N. Jet impingement heat transfer: Physics, correlations, and numerical modeling. Adv. Heat Transf. 2006, 39, 565–631. [Google Scholar]
- Carlomagno, G.M.; Ianiro, A. Thermo-fluid-dynamics of submerged jets impinging at short nozzle-to-plate distance: A review. Int. J. Exp. Therm. Fluid Sci. 2014, 58, 15–35. [Google Scholar]
- Zumbrunnen, D.A.; Aziz, M. Convective heat transfer enhancement due to intermittency in an impinging jet. ASME J. Heat Transf. 1993, 115, 91–98. [Google Scholar]
- Sheriff, H.; Zumbrunnen, D. Effect of flow pulsations on the cooling effectiveness of an impinging jet. ASME J. Heat Transf. 1994, 116, 886–895. [Google Scholar]
- Azevedo, L.F.A.; Webb, B.W.; Queiroz, M. Pulsed air jet impingement heat transfer. Int. J. Exp. Therm. Fluid Sci. 1994, 8, 206–213. [Google Scholar]
- Sailor, D.J.; Rohli, D.J.; Fu, Q.L. Effect of variable duty cycle flow pulsations on heat transfer enhancement for an impinging air jet. Int. J. Heat Fluid Flow 1999, 20, 574–580. [Google Scholar]
- Herwig, H.; Mocikat, H.; Guertler, T.; Goeppert, S. Heat transfer due to unsteadily impinging jets. Int. J. Therm. Sci. 2004, 43, 733–741. [Google Scholar]
- Hofmann, H.M.; Movileanu, D.L.; Kind, M.; Martin, H. Influence of a pulsation on heat transfer and flow structure in submerged impinging jets. Int. J. Heat Mass Transf. 2007, 50, 3638–3648. [Google Scholar]
- Herwig, H.; Middelberg, G. The physics of unsteady jet impingement and its heat transfer performance. Acta Mech. 2008, 201, 171–184. [Google Scholar]
- Middelberg, G.; Herwig, H. Convective heat transfer under unsteady impinging jets: The effect of the shape of the unsteadiness. Heat Mass Transf. 2009, 45, 1519–1532. [Google Scholar]
- Zhou, J.W.; Wang, Y.G.; Middelberg, G.; Herwig, H. Unsteady jet impingement: Heat transfer on smooth and non-smooth surfaces. Int. Commun. Heat Mass Transf. 2009, 36, 103–110. [Google Scholar]
- Persoons, T.; Balgazin, K.; Brown, K.; Murray, D.B. Scaling of convective heat transfer enhancement due to flow pulsation in an axisymmetric impinging jet. ASME J. Heat Transf. 2013, 135, 111012. [Google Scholar]
- Geng, L.P.; Zheng, C.B.; Zhou, J.W. Heat transfer characteristics of impinging jets: The influence of unsteadiness with different waveforms. Int. Comm. Heat Mass Transf. 2015, 66, 105–113. [Google Scholar]
- Tang, C.; Zhang, J.Z.; Lyu, Y.W.; Tan, X.M. Convective heat transfer on a flat target surface impinged by pulsating jet with an additional transmission chamber. Heat Mass Transf. 2020, 56, 183–205. [Google Scholar]
- Liewkongsataporn, W.; Patterson, T.; Ahrens, F. Pulsating jet impingement heat transfer enhancement. Dry. Technol. 2008, 26, 433–442. [Google Scholar]
- Xu, P.; Yu, B.; Qiu, S.X.; Poh, H.J.; Mujumdar, A.S. Turbulent impinging jet heat transfer enhancement due to intermittent pulsation. Int. J. Therm. Sci. 2010, 49, 1247–1252. [Google Scholar]
- Pakhomov, M.A.; Terekhov, V.I. Effect of pulse frequency on heat transfer at the stagnation point of an impinging turbulent jet. High Temp. 2013, 51, 256–261. [Google Scholar]
- Mohammadpour, J.; Rajabi-Zargarabadi, M.; Mujumdar, A.S.; Ahmadi, H. Effect of intermittent and sinusoidal pulsed flows on impingement heat transfer from a concave surface. Int. J. Therm. Sci. 2014, 76, 118–127. [Google Scholar]
- Pakhomov, M.A.; Terekhov, V.I. Numerical study of fluid flow and heat transfer characteristics in an intermittent turbulent impinging round jet. Int. J. Therm. Sci. 2015, 87, 85–93. [Google Scholar]
- Craft, T.J.; Launder, B.E. New wall-reflection model applied to the turbulent impinging jet. AIAA J. 1992, 30, 2970–2972. [Google Scholar]
- Baughn, J.W.; Shimizu, S. Heat transfer measurements from a surface with uniform heat flux and an impinging jet. ASME J. Heat Transf. 1989, 111, 1096–1098. [Google Scholar]
- Baughn, J.W.; Hechanova, A.; Yan, X. An experimental study of entrainment effects on the heat transfer from a flat surface to a heated circular impinging jet. ASME J. Heat Transf. 1991, 113, 1023–1025. [Google Scholar]
- Behnia, M.; Parneix, S.; Durbin, P.A. Prediction of heat transfer in an axisymmetric turbulent jet impinging on a flat plate. Int. J. Heat Mass Transf. 1998, 41, 1845–1855. [Google Scholar]
- Merci, B.; Dick, E. Heat transfer predictions with a cubic k-ε model for axisymmetric turbulent jets impinging onto a flat plate. Int. J. Heat Mass Transf. 2003, 46, 469–480. [Google Scholar]
- Volkov, K.N. Unsteady-state heat transfer in the region of interaction between a turbulent jet and an obstacle. High Temp. 2007, 45, 818–825. [Google Scholar]













© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pakhomov, M.A.; Terekhov, V.I. RANS Simulation of the Effect of Pulse Form on Fluid Flow and Convective Heat Transfer in an Intermittent Round Jet Impingement. Energies 2020, 13, 4025. https://doi.org/10.3390/en13154025
Pakhomov MA, Terekhov VI. RANS Simulation of the Effect of Pulse Form on Fluid Flow and Convective Heat Transfer in an Intermittent Round Jet Impingement. Energies. 2020; 13(15):4025. https://doi.org/10.3390/en13154025
Chicago/Turabian StylePakhomov, M. A., and V. I. Terekhov. 2020. "RANS Simulation of the Effect of Pulse Form on Fluid Flow and Convective Heat Transfer in an Intermittent Round Jet Impingement" Energies 13, no. 15: 4025. https://doi.org/10.3390/en13154025
APA StylePakhomov, M. A., & Terekhov, V. I. (2020). RANS Simulation of the Effect of Pulse Form on Fluid Flow and Convective Heat Transfer in an Intermittent Round Jet Impingement. Energies, 13(15), 4025. https://doi.org/10.3390/en13154025