Selection of Temporal Lags for Predicting Riverflow Series from Hydroelectric Plants Using Variable Selection Methods
Abstract
:1. Introduction
- Li et al. [22]—to increase the estimation of growing stem volume of pine using optical images;
- Bonah et al. [23]—to quantitative tracking of foodborne pathogens;
- Xiong et al. [24]—to increase near-infrared spectroscopy quality;
- Speiser et al. [25]—an extensive investigation with 311 datasets to compare several random forest VS methods for classification;
- Rendall et al. [26]—extensive comparison of large scale data driven prediction methods based on VS and machine learning;
- Marcjasz et al. [27]—to electricity price forecasting;
- Santi et al. [28]—to predict mathematics scores of students;
- Karim et al. [29]—to predict post-operative outcomes of cardiac surgery patients;
- Kim and Kang [30]—to faulty wafer detection in semiconductor manufacturing;
- Furmańczyk and Rejchel [31]—to high-dimensional binary classification problems;
- Fouad and Loáiciga [5]—to predict percentile flows using inflow duration curve and regression models;
- Ata Tutkun and Kayhan Atilgan [32]—investigated VS models in Cox regression, a multivariate model;
- Mehmood et al. [33]—compared several VS approaches in partial least-squares regression tasks;
- McGee and Yaffee [34]—provided a study on short multivariate time series and many variations of Least Absolute Shrinkage and Selection Operator (LASSO) for VS;
- Seo [35]—discussed the VS problem together with outlier detection, due to each input affecting the regression task;
- Dong et al. [36]—to wind power generation prediction;
- Sigauke et al. [37]—presented a probabilistic hourly load forecasting framework based on additive quantile regression models;
- Wang et al. [38]—to short-term wind speed forecasting;
- Taormina and Chau [39]—to rainfall-runoff modeling;
- Taormina et al. [40]—to river flow forecasting;
- Cui and Jiang [41]—to chaotic time series prediction;
- Silva et al. [42]—to predict the price of sugarcane derivatives;
- Siqueira et al. [2]—use of VS methods, such as wrappers and filters to predict streamflow series; and
- Kachba et al. [46]—application of wrapper and non-linear filters to estimate the impact of air pollution on human health.
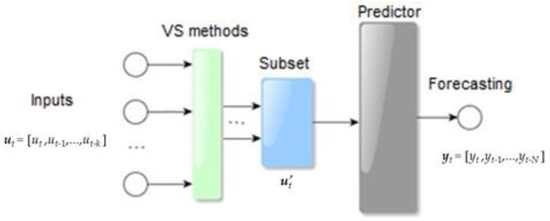
2. Variable Selection
- Relevance: the concept associated with the importance of a given variable may have to the problem, since the information it contains will be the basis of the selection process. The relevance is strong or weak depending on how much its removal degrades the performance of the predictor;
- Redundancy: two or more variables are redundant if their observed values are highly correlated or dependent. The level of this correlation reveals the degree of redundancy; and
- Optimality: a so-called optimal subset of input variables is when there is no other subset that produces better results.
Variable Selection in Streamflow Series Forecasting
3. Filters
3.1. Partial Autocorrelation Function
3.2. Mutual Information
3.3. Partial Mutual Information
3.4. Normalization of Maximum Relevance and Minimum Common Redundancy Mutual Information
4. Wrappers
4.1. Progressive Selection
4.2. Evaluation Functions
5. Bio-Inspired Metaheuristics
5.1. Genetic Algorithm
5.2. Particle Swarm Optimization
6. Case Study
- Training, from January 1st, 1931 to December 31st, 1995 (780 samples);
- Validation, from January 1st, 1996 to December 31st, 2005 (120 samples); and
- Test, from January 1st, 2006 to December 31st, 2015 (120 samples).
6.1. Predictors
6.2. Computational Results
6.3. Discussion
7. Conclusions
- Mean square error (MSE);
- Bayesian information criterion (BIC);
- Bayesian information criterion (AIC).
- The linear filters used were the:
- Partial autocorrelation function (PACF);
- PACF using the Stedinger [52] approach for hydrological series.
- The nonlinear filters addressed were:
- Mutual Information (MI);
- Partial mutual information (PMI); and
- Normalization of maximum relevance and minimum common redundancy mutual information (N-MRMCR-MI).
- Particle swarm optimization (PSO); and
- Genetic algorithm (GA).
- The selected lags were very diverse depending on the method, especially for the monthly case;
- For the annual approaches, some draws could be found;
- The linear models perform better with filters;
- The wrapper is the best choice for the neural network; and
- Regarding the forecasting methods, the monthly ELM achieved the best error values.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Month | BIC | AIC | W-MSE | PACF | PACF -Sted. | MI | PMI | N-MRMCR -MI | GA | PSO | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PAR | J | 1(1) | 1(1) | 5(1,3,4,5,6) | 1(1) | 1(1) | 1(1) | 1(1) | 3(1,5,6) | 5(1,3,4,5,6) | 5(12,3,4,6) |
| F | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 2(1,6) | 1(1) | 2(1,2) | 1(1) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 3(2,4,6) | |
| M | 1(1) | 2(1,2) | 6(1,2,3,4,5,6) | 2(1,6) | 1(1) | 2(1,2) | 1(1) | 5(1,2,3,4,5,5) | 6(1,2,3,4,5,6) | 2(1,5) | |
| A | 2(1,2) | 3(1,2,3) | 6(1,2,3,4,5,6) | 2(1,2) | 2(1,2) | 4(1,2,3,4) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 3(1,3,5) | |
| M | 4(1,2,3,4) | 4(1,2,3,4) | 6(1,2,3,4,5,6) | 3(1,2,3) | 3(1,2,3) | 5(1,2,3,4,5) | 2(1,3) | 4(1,3,4,6) | 6(1,2,3,4,5,6) | 3(1,2,3) | |
| J | 2(1,2) | 2(1,2) | 6(1,2,3,4,5,6) | 2(1,2) | 2(1,2) | 6(1,2,3,4,5,6) | 3(1,2,5) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 2(1,4) | |
| J | 2(1,2) | 2(1,2) | 6(1,2,3,4,5,6) | 2(1,2) | 2(1,2) | 6(1,2,3,4,5,6) | 4(1,2,4,5) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 5(1,2,4,5,6) | |
| A | 1(1) | 4(1,2,3,4) | 6(1,2,3,4,5,6) | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 4(1,3,5,6) | |
| S | 4(1,2,3,4) | 4(1,2,3,4) | 6(1,2,3,4,5,6) | 4(1,2,3,4) | 4(1,2,3,4) | 6(1,2,3,4,5,6) | 1(1) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 4(1,2,3,6) | |
| O | 2(3,4) | 3(3,4,6) | 6(1,2,3,4,5,6) | 4(1,2,3,4) | 4(1,2,3,4) | 6(1,2,3,4,5,6) | 1(2) | 6(1,2,3,4,5,6) | 5(1,2,3,4,6) | 4(1,3,4,6) | |
| N | 1(1) | 2(1,2) | 6(1,2,3,4,5,6) | 2(1,5) | 1(1) | 6(1,2,3,4,5,6) | 2(1,2) | 6(1,2,3,4,5,6) | 5(1,2,3,4,5) | 4(1,2,4,5) | |
| D | 2(1,2) | 2(1,2) | 6(1,2,3,4,5,6) | 3(1,2,6) | 2(1,2) | 4(1,2,3,4) | 1(1) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 2(4,5) | |
| ELM | J | 1(2) | 1(2) | 1(2) | 1(1) | 1(1) | 1(1) | 1(1) | 3(1,5,6) | 2(1,4) | 1(1) |
| F | 1(1) | 1(1) | 1(1) | 2(1,6) | 1(1) | 2(1,2) | 1(1) | 6(1,2,3,4,5,6) | 2(1,4) | 5(1,3,4,5,6) | |
| M | 1(1) | 1(1) | 2(3,6) | 2(1,6) | 1(1) | 2(1,2) | 1(1) | 5(1,2,3,4,5,5) | 5(1,2,3,4,5) | 3(1,3,4) | |
| A | 1(5) | 1(5) | 1(5) | 2(1,2) | 2(1,2) | 4(1,2,3,4) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 2(1,2) | 4(1,2,4,5) | |
| M | 1(2) | 1(2) | 1(2) | 3(1,2,3) | 3(1,2,3) | 5(1,2,3,4,5) | 2(1,3) | 4(1,3,4,6) | 2(2,3) | 3(1,2,3) | |
| J | 1(1) | 1(1) | 1(1) | 2(1,2) | 2(1,2) | 6(1,2,3,4,5,6) | 3(1,2,5) | 6(1,2,3,4,5,6) | 1(1) | 1(1) | |
| J | 1(1) | 1(1) | 1(1) | 2(1,2) | 2(1,2) | 6(1,2,3,4,5,6) | 4(1,2,4,5) | 6(1,2,3,4,5,6) | 2(1,6) | 1(1) | |
| A | 1(1) | 1(1) | 1(1) | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 4(1,2,3,5) | 1(3) | |
| S | 1(1) | 1(1) | 1(1) | 4(1,2,3,4) | 4(1,2,3,4) | 6(1,2,3,4,5,6) | 1(1) | 6(1,2,3,4,5,6) | 1(1) | 2(1,3) | |
| O | 1(1) | 1(1) | 1(1) | 4(1,2,3,4) | 4(1,2,3,4) | 6(1,2,3,4,5,6) | 1(2) | 6(1,2,3,4,5,6) | 1(1) | 3(1,2,6) | |
| N | 1(5) | 1(5) | 2(2,5) | 2(1,5) | 1(1) | 6(1,2,3,4,5,6) | 2(1,2) | 6(1,2,3,4,5,6) | 1(1) | 3(2,3,5) | |
| D | 1(2) | 1(2) | 1(2) | 3(1,2,6) | 2(1,2) | 4(1,2,3,4) | 1(1) | 6(1,2,3,4,5,6) | 1(2) | 2(2,6) | |
| AR | 2(1,2) | 2(1,2) | 4(1,2,3,5) | 3(1,2,3) | 3(1,2,3) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 4(1,2,3,5) | 4(1,2,3,5) | |
| ELM | 1(1) | 2(1,4) | 6(1,2,3,4,5,6) | 3(1,2,3) | 3(1,2,3) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 4(1,2,3,5) | 5(1,2,4,5,6) | |
| Month | BIC | AIC | W-MSE | PACF |
PACF -Sted. | MI | PMI |
N-MRMCR -MI | GA | PSO | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PAR | J | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 2(1,6) | 1(1) | 1(6) | 1(6) | 1(1) | 6(1,2,3,4,5,6) | 3(4,5,6) |
| F | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 1(1) | 1(1) | 1(1) | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 4(1,2,4,5) | |
| M | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 1(1) | 1(1) | 2(1,2) | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 2(3,4) | |
| A | 3(1,2,5) | 3(1,2,5) | 6(1,2,3,4,5,6) | 3(1,2,5) | 2(1,2) | 3(1,2,3) | 2(1,2) | 2(1,2) | 6(1,2,3,4,5,6) | 1(4) | |
| M | 4(1,2,3,5) | 4(1,2,3,5) | 6(1,2,3,4,5,6) | 2(1,3) | 1(1) | 5(1,2,3,4,5) | 6(1,2,3,4,5,6) | 3(1,2,3) | 6(1,2,3,4,5,6) | 2(5,6) | |
| J | 3(1,3,5) | 4(1,2,3,5) | 5(1,2,3,5,6) | 1(1) | 1(1) | 5(1,2,3,4,5) | 3(1,2,5) | 2(1,2) | 5(1,2,3,5,6) | 2(1,2) | |
| J | 3(1,2,6) | 3(1,2,6) | 3(1,2,6) | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 2(1,2) | 2(1,2) | 3(1,2,6) | 1(1) | |
| A | 1(1) | 1(1) | 1(1) | 2(1,3) | 1(1) | 6(1,2,3,4,5,6) | 2(1,2) | 1(1) | 1(1) | 2(1,2) | |
| S | 1(1) | 1(1) | 2(1,2) | 2(1,3) | 1(1) | 6(1,2,3,4,5,6) | 2(1,2) | 4(1,2,3,4) | 2(1,2) | 2(1,2) | |
| O | 1(1) | 1(1) | 3(1,2,3) | 4(1,3,4,6) | 1(1) | 6(1,2,3,4,5,6) | 1(1) | 4(1,2,3,4) | 3(1,2,3) | 1(2) | |
| N | 2(1,2) | 2(1,2) | 4(1,2,3,4) | 3(1,2,5) | 2(1,2) | 1(1) | 1(1) | 1(1) | 4(1,2,3,4) | 2(4,5) | |
| D | 1(1) | 1(1) | 5(1,2,3,4,5) | 3(1,5,6) | 1(1) | 2(1,2) | 2(1,6) | 2(1,2) | 5(1,2,3,4,5) | 3(1,2,3) | |
| ELM | J | 1(2) | 1(2) | 3(1,2,6) | 2(1,6) | 1(1) | 1(6) | 1(6) | 1(1) | 4(1,2,3,5) | 3(4,5,6) |
| F | 1(1) | 1(1) | 2(1,5) | 1(1) | 1(1) | 1(1) | 1(1) | 1(1) | 2(1,4) | 2(1,3) | |
| M | 1(1) | 1(1) | 2(2,3) | 1(1) | 1(1) | 2(1,2) | 1(1) | 1(1) | 1(2) | 5(1,2,4,5,6) | |
| A | 1(5) | 1(5) | 1(5) | 3(1,2,5) | 2(1,2) | 3(1,2,3) | 2(1,2) | 2(1,2) | 1(3) | 1(5) | |
| M | 1(2) | 1(2) | 1(2) | 2(1,3) | 1(1) | 5(1,2,3,4,5) | 6(1,2,3,4,5,6) | 3(1,2,3) | 2(1,4) | 2(1,5) | |
| J | 1(1) | 1(1) | 3(1,5,6) | 1(1) | 1(1) | 5(1,2,3,4,5) | 3(1,2,5) | 2(1,2) | 2(1,5) | 5(1,2,3,4,5) | |
| J | 1(1) | 1(1) | 2(1,2) | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 2(1,2) | 2(1,2) | 2(1,6) | 4(1,3,4,6) | |
| A | 1(1) | 1(1) | 3(1,4,5) | 2(1,3) | 1(1) | 6(1,2,3,4,5,6) | 2(1,2) | 1(1) | 2(1,6) | 4(1,2,3,5) | |
| S | 1(1) | 1(1) | 3(1,5,6) | 2(1,3) | 1(1) | 6(1,2,3,4,5,6) | 2(1,2) | 4(1,2,3,4) | 5(1,2,4,5,6) | 3(2,5,6) | |
| O | 1(1) | 1(1) | 3(1,3,4) | 4(1,3,4,6) | 1(1) | 6(1,2,3,4,5,6) | 1(1) | 4(1,2,3,4) | 5(1,2,3,4,5) | 4(1,2,4,6) | |
| N | 1(5) | 1(5) | 3(1,4,5) | 3(1,2,5) | 2(1,2) | 1(1) | 1(1) | 1(1) | 2(1,3) | 3(1,2,3) | |
| D | 1(2) | 1(2) | 2(2,5) | 3(1,5,6) | 1(1) | 2(1,2) | 2(1,6) | 2(1,2) | 3(1,2,5) | 4(2,4,5,6) | |
| AR | 2(1,2) | 2(1,2) | 2(1,2) | 4(1,2,3,4) | 4(1,2,3,4) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 2(1,2) | 2(1,2) | |
| ELM | 1(1) | 2(1,4) | 6(1,2,3,4,5,6) | 4(1,2,3,4) | 4(1,2,3,4) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 4(1,2,4,5,6) | |
| Month | BIC | AIC | W-MSE | PACF | PACF -Sted. | MI | PMI | N-MRMCR -MI | GA | PSO | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PAR | J | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 1(1) | 1(1) | 3(1,2,3) | 1(1) | 4(1,4,5,6) | 6(1,2,3,4,5,6) | 2(3,6) |
| F | 3(1,3,5) | 3(1,3,5) | 6(1,2,3,4,5,6) | 3(1,4,5) | 1(1) | 4(1,2,4,5) | 1(1) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 2(1,4) | |
| M | 1(1) | 1(1) | 5(1,2,3,4,6) | 1(1) | 1(1) | 2(1,2) | 1(1) | 6(1,2,3,4,5,6) | 5(1,2,3,4,6) | 3(1,2,5) | |
| A | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 1(1) | 1(1) | 5(1,2,3,4,6) | 1(5) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 3(2,4,6) | |
| M | 1(1) | 2(1,3) | 6(1,2,3,4,5,6) | 1(1) | 1(1) | 4(1,2,3,4) | 2(1,3) | 5(1,2,4,5,6) | 6(1,2,3,4,5,6) | 3(1,3,4) | |
| J | 5(1,2,3,5,6) | 5(1,2,3,5,6) | 6(1,2,3,4,5,6) | 3(1,2,3) | 3(1,2,3) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | |
| J | 5(1,2,3,4,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 2(1,2) | 6(1,2,3,4,5,6) | 5(1,2,3,5,6) | 2(1,3) | |
| A | 1(1) | 1(1) | 5(1,2,3,4,5) | 2(1,2) | 2(1,2) | 6(1,2,3,4,5,6) | 3(1,5,4) | 6(1,2,3,4,5,6) | 5(1,2,3,4,5) | 4(1,2,3,5) | |
| S | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 2(1,2) | 2(1,2) | 6(1,2,3,4,5,6) | 2(1,2) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 5(1,2,3,4,5) | |
| O | 1(1) | 1(1) | 4(1,2,3,4) | 2(1,2) | 2(1,2) | 6(1,2,3,4,5,6) | 3(1,2,6) | 6(1,2,3,4,5,6) | 4(1,2,3,4) | 6(1,2,3,4,5,6) | |
| N | 1(1) | 2(1,3) | 2(1,3) | 1(1) | 1(1) | 5(1,2,3,4,5) | 1(1) | 6(1,2,3,4,5,6) | 2(1,3) | 1(1) | |
| D | 1(1) | 1(1) | 5(1,2,3,4,5) | 2(1,6) | 1(1) | 2(1,2) | 1(1) | 6(1,2,3,4,5,6) | 5(1,2,3,4,5) | 1(6) | |
| ELM | J | 1(2) | 1(2) | 1(3) | 1(1) | 1(1) | 3(1,2,3) | 1(1) | 4(1,4,5,6) | 1(3) | 3(1,3,5) |
| F | 1(1) | 1(1) | 3(1,2,6) | 3(1,4,5) | 1(1) | 4(1,2,4,5) | 1(1) | 6(1,2,3,4,5,6) | 2(1,6) | 4(1,2,5,6) | |
| M | 1(1) | 1(1) | 2(1,3) | 1(1) | 1(1) | 2(1,2) | 1(1) | 6(1,2,3,4,5,6) | 3(1,5,6) | 3(1,4,6) | |
| A | 1(5) | 1(5) | 3(1,2,4) | 1(1) | 1(1) | 5(1,2,3,4,6) | 1(5) | 6(1,2,3,4,5,6) | 2(1,6) | 5(1,2,3,5,6) | |
| M | 1(2) | 1(2) | 1(1) | 1(1) | 1(1) | 4(1,2,3,4) | 2(1,3) | 5(1,2,4,5,6) | 2(1,3) | 1(1) | |
| J | 1(1) | 1(1) | 2(1,4) | 3(1,2,3) | 3(1,2,3) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 5(1,2,4,5,6) | 3(1,3,6) | |
| J | 1(1) | 1(1) | 1(1) | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 2(1,2) | 6(1,2,3,4,5,6) | 1(1) | 2(1,4) | |
| A | 1(1) | 1(1) | 1(1) | 2(1,2) | 2(1,2) | 6(1,2,3,4,5,6) | 3(1,5,4) | 6(1,2,3,4,5,6) | 1(1) | 2(1,2) | |
| S | 1(1) | 1(1) | 2(1,5) | 2(1,2) | 2(1,2) | 6(1,2,3,4,5,6) | 2(1,2) | 6(1,2,3,4,5,6) | 2(1,2) | 3(1,4,5) | |
| O | 1(1) | 1(1) | 5(1,2,4,5,6) | 2(1,2) | 2(1,2) | 6(1,2,3,4,5,6) | 3(1,2,6) | 6(1,2,3,4,5,6) | 1(3) | 4(1,4,5,6) | |
| N | 1(5) | 1(5) | 2(1,3) | 1(1) | 1(1) | 5(1,2,3,4,5) | 1(1) | 6(1,2,3,4,5,6) | 1(3) | 4(1,4,5,6) | |
| D | 1(2) | 1(2) | 4(2,3,5,6) | 2(1,6) | 1(1) | 2(1,2) | 1(1) | 6(1,2,3,4,5,6) | 1(2) | 5(1,2,3,4,5) | |
| AR | 2(1,3) | 2(1,3) | 2(1,3) | 2(1,3) | 3(1,3,4) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 2(1,3) | 2(1,3) | |
| ELM | 1(1) | 2(1,4) | 6(1,2,3,4,5,6) | 1(1) | 3(1,3,4) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 2(1,4) | |
| Month | BIC | AIC | W-MSE | PACF | PACF -Sted. | MI | PMI | N-MRMCR -MI | GA | PSO | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PAR | J | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 2(1,5) | 1(1) | 3(1,5,6) | 1(1) | 1(1) | 5(1,3,4,5,6) | 3(3,4,6) |
| F | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 2(1,6) | 1(1) | 1(1) | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 2(5,6) | |
| M | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 2(1,6) | 1(1) | 2(1,2) | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 3(3,5,6) | |
| A | 3(1,2,6) | 3(1,2,6) | 4(1,2,5,6) | 2(1,2) | 2(1,2) | 3(1,2,4) | 1(1) | 2(1,2) | 4(1,2,5,6) | 2(2,3) | |
| M | 4(1,2,3,5) | 4(1,2,3,5) | 5(1,2,3,4,5) | 3(1,2,3) | 3(1,2,3) | 5(1,2,3,4,5) | 2(1,2) | 3(1,2,3) | 5(1,2,3,4,5) | 3(2,5,6) | |
| J | 1(1) | 1(1) | 5(1,2,4,5,6) | 1(1) | 1(1) | 5(1,2,3,4,5) | 6(1,2,3,4,5,6) | 2(1,2) | 5(1,2,4,5,6) | 4(2,3,4,5) | |
| J | 3(1,2,3) | 3(1,2,3) | 6(1,2,3,4,5,6) | 2(1,2) | 2(1,2) | 6(1,2,3,4,5,6) | 2(1,2) | 2(1,2) | 6(1,2,3,4,5,6) | 1(3) | |
| A | 1(1) | 5(1,2,3,4,6) | 6(1,2,3,4,5,6) | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 1(1) | 6(1,2,3,4,5,6) | 5(2,3,4,5,6) | |
| S | 2(1,3) | 2(1,3) | 6(1,2,3,4,5,6) | 2(1,2) | 2(1,2) | 6(1,2,3,4,5,6) | 1(1) | 4(1,2,3,4) | 6(1,2,3,4,5,6) | 1(1) | |
| O | 2(1,3) | 3(1,3,6) | 6(1,2,3,4,5,6) | 3(1,2,3) | 3(1,2,3) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 4(1,2,3,4) | 6(1,2,3,4,5,6) | 1(1) | |
| N | 1(1) | 2(1,2) | 6(1,2,3,4,5,6) | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 4(1,2,5,6) | |
| D | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 1(1) | 1(1) | 5(1,2,3,4,5) | 1(1) | 2(1,2) | 6(1,2,3,4,5,6) | 1(4) | |
| ELM | J | 1(2) | 1(2) | 2(1,6) | 2(1,5) | 1(1) | 3(1,5,6) | 1(1) | 1(1) | 5(1,2,3,4,6) | 4(1,2,4,6) |
| F | 1(1) | 1(1) | 1(1) | 2(1,6) | 1(1) | 1(1) | 1(1) | 1(1) | 4(1,2,3,6) | 4(1,2,4,5) | |
| M | 1(1) | 1(1) | 2(1,2) | 2(1,6) | 1(1) | 2(1,2) | 1(1) | 1(1) | 2(1,2) | 6(1,2,3,4,5,6) | |
| A | 1(5) | 1(5) | 2(1,2) | 2(1,2) | 2(1,2) | 3(1,2,4) | 1(1) | 2(1,2) | 2(1,2) | 4(1,2,3,5) | |
| M | 1(2) | 1(2) | 1(1) | 3(1,2,3) | 3(1,2,3) | 5(1,2,3,4,5) | 2(1,2) | 3(1,2,3) | 4(1,2,4,6) | 4(2,3,5,6) | |
| J | 1(1) | 1(1) | 3(1,2,6) | 1(1) | 1(1) | 5(1,2,3,4,5) | 6(1,2,3,4,5,6) | 2(1,2) | 2(2,5) | 3(1,2,4) | |
| J | 1(1) | 1(1) | 2(1,2) | 2(1,2) | 2(1,2) | 6(1,2,3,4,5,6) | 2(1,2) | 2(1,2) | 2(1,2) | 3(1,2,5) | |
| A | 1(1) | 1(1) | 3(1,2,5) | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 1(1) | 5(1,2,3,4,5) | 2(1,2) | |
| S | 1(1) | 1(1) | 2(4,6) | 2(1,2) | 2(1,2) | 6(1,2,3,4,5,6) | 1(1) | 4(1,2,3,4) | 2(2,6) | 2(5,6) | |
| O | 1(1) | 1(1) | 2(1,6) | 3(1,2,3) | 3(1,2,3) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 4(1,2,3,4) | 3(1,3,4) | 3(1,2,5) | |
| N | 1(5) | 1(5) | 1(6) | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 1(1) | 1(1) | 2(2,5) | 4(2,3,5,6) | |
| D | 1(2) | 1(2) | 3(2,3,4) | 1(1) | 1(1) | 5(1,2,3,4,5) | 1(1) | 2(1,2) | 1(2) | 2(2,6) | |
| AR | 2(1,2) | 2(1,2) | 2(1,2) | 3(1,2,3) | 3(1,2,3) | 6(1,2,3,4,5,6) | 2(1,3) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | |
| ELM | 1(1) | 2(1,4) | 6(1,2,3,4,5,6) | 3(1,2,3) | 3(1,2,3) | 6(1,2,3,4,5,6) | 2(1,3) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 4(1,2,3,4) | |
| Month | BIC | AIC | W-MSE | PACF | PACF -Sted. | MI | PMI | N-MRMCR -MI | GA | PSO | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PAR | J | 2(1,2) | 2(1,2) | 6(1,2,3,4,5,6) | 3(1,5,6) | 1(1) | 3(1,2,4) | 1(1) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 5(1,2,4,5,6) |
| F | 2(1,3) | 3(1,3,5) | 5(1,3,4,5,6) | 1(1) | 1(1) | 3(1,2,3) | 1(1) | 6(1,2,3,4,5,6) | 5(1,3,4,5,6) | 3(2,5,6) | |
| M | 1(1) | 2(1,6) | 5(1,2,3,4,6) | 2(1,2) | 2(1,2) | 6(1,2,3,4,5,6) | 1(1) | 6(1,2,3,4,5,6) | 5(1,2,3,4,6) | 2(2,5) | |
| A | 1(2) | 1(2) | 6(1,2,3,4,5,6) | 3(1,2,4) | 2(1,2) | 5(1,2,3,4,5) | 3(1,2,3) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 3(1,5,6) | |
| M | 1(1) | 2(1,5) | 4(1,3,5,6) | 5(1,2,3,4,6) | 4(1,2,3,4) | 6(1,2,3,4,5,6) | 2(1,6) | 6(1,2,3,4,5,6) | 4(1,3,5,6) | 2(2,3) | |
| J | 1(1) | 2(1,2) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 4(1,2,3,5) | 3(1,2,5) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 3(1,3,5) | |
| J | 3(1,2,4) | 3(1,2,4) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 5(1,2,3,4,6) | 2(1,3) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 4(3,4,5,6) | |
| A | 1(1) | 3(1,2,5) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 5(1,2,3,4,5) | 2(1,5) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 3(2,3,6) | |
| S | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 2(1,3) | 2(1,3) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 3(2,4,5) | |
| O | 1(1) | 3(1,2,4) | 5(1,2,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 2(1,4) | 2(1,4) | 6(1,2,3,4,5,6) | 5(1,2,4,5,6) | 2(3,4) | |
| N | 3(1,2,3) | 4(1,2,3,5) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 2(1,3) | 2(1,3) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 2(5,6) | |
| D | 1(1) | 2(1,4) | 6(1,2,3,4,5,6) | 5(1,2,3,4,6) | 4(1,2,3,4) | 3(1,2,4) | 1(1) | 6(1,2,3,4,5,6) | 5(1,3,4,5,6) | 1(1) | |
| ELM | J | 1(2) | 1(2) | 1(2) | 3(1,5,6) | 1(1) | 3(1,2,4) | 1(1) | 6(1,2,3,4,5,6) | 2(1,4) | 3(1,3,4) |
| F | 1(1) | 1(1) | 1(1) | 1(1) | 1(1) | 3(1,2,3) | 1(1) | 6(1,2,3,4,5,6) | 2(1,2) | 5(1,2,3,4,6) | |
| M | 1(1) | 1(1) | 2(3,6) | 2(1,2) | 2(1,2) | 6(1,2,3,4,5,6) | 1(1) | 6(1,2,3,4,5,6) | 2(1,2) | 3(1,3,6) | |
| A | 1(5) | 1(5) | 1(5) | 3(1,2,4) | 2(1,2) | 5(1,2,3,4,5) | 3(1,2,3) | 6(1,2,3,4,5,6) | 2(1,2) | 3(1,3,4) | |
| M | 1(2) | 1(2) | 1(2) | 5(1,2,3,4,6) | 4(1,2,3,4) | 6(1,2,3,4,5,6) | 2(1,6) | 6(1,2,3,4,5,6) | 1(4) | 4(1,2,3,6) | |
| J | 1(1) | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 4(1,2,3,5) | 3(1,2,5) | 6(1,2,3,4,5,6) | 2(2,5) | 1(1) | |
| J | 1(1) | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 5(1,2,3,4,6) | 2(1,3) | 6(1,2,3,4,5,6) | 3(2,3,6) | 2(1,5) | |
| A | 1(1) | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 5(1,2,3,4,5) | 2(1,5) | 6(1,2,3,4,5,6) | 3(3,4,5) | 3(2,3,5) | |
| S | 1(1) | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 2(1,3) | 2(1,3) | 6(1,2,3,4,5,6) | 4(1,2,4,5) | 3(2,3,5) | |
| O | 1(1) | 1(1) | 1(1) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 2(1,4) | 2(1,4) | 6(1,2,3,4,5,6) | 3(1,4,5) | 3(2,4,6) | |
| N | 1(5) | 1(5) | 2(2,5) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 2(1,3) | 2(1,3) | 6(1,2,3,4,5,6) | 3(1,2,3) | 1(1) | |
| D | 1(2) | 1(2) | 1(2) | 5(1,2,3,4,6) | 4(1,2,3,4) | 3(1,2,4) | 1(1) | 6(1,2,3,4,5,6) | 3(1,4,5) | 2(1,3) | |
| AR | 2(1,2) | 2(1,2) | 2(1,2) | 3(1,2,3) | 3(1,2,3) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 2(1,2) | 2(1,2) | |
| ELM | 1(1) | 2(1,4) | 6(1,2,3,4,5,6) | 3(1,2,3) | 3(1,2,3) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 6(1,2,3,4,5,6) | 4(1,2,3,6) | |
References
- IHA—International Hydropower Association. Hydropower Status Report: Sector Trends and Insights. 2020. Available online: https://www.hydropower.org/publications/2020-hydropower-status-report (accessed on 15 May 2020).
- Siqueira, H.V.; Boccato, L.; Luna, I.; Attux, R.; Lyra, C. Performance analysis of unorganized machines in streamflow forecasting of Brazilian plants. Appl. Soft Comput. 2018, 68, 494–506. [Google Scholar] [CrossRef]
- Zhu, S.; Zhou, J.; Ye, L.; Meng, C. Streamflow estimation by support vector machine coupled with different methods of time series decomposition in the upper reaches of Yangtze River, China. Environ. Earth Sci. 2016, 75, 531. [Google Scholar] [CrossRef]
- Dilini, W.; Attygalle, D.; Hansen, L.L.; Nandalal, K.W. Ensemble Forecast for monthly Reservoir Inflow; A Dynamic Neural Network Approach. In Proceedings of the 4th Annual International Conference on Operations Research and Statistics (ORS 2016), Global Science and Technology Forum, Singapore, 18–19 January 2016; pp. 84–90. [Google Scholar]
- Fouad, G.; Loáiciga, H.A. Independent variable selection for regression modeling of the flow duration curve for ungauged basins in the United States. J. Hydrol. 2020, 587, 124975. [Google Scholar] [CrossRef]
- Arsenault, R.; Côté, P. Analysis of the effects of biases in ensemble streamflow prediction (ESP) forecasts on electricity production in hydropower reservoir management. Hydrol. Earth Syst. Sci. 2019, 23, 2735–2750. [Google Scholar] [CrossRef] [Green Version]
- Stojković, M.; Kostić, S.; Prohaska, S.; Plavsic, J.; Tripković, V. A new approach for trend assessment of annual streamflows: A case study of hydropower plants in Serbia. Water Resour. Manag. 2017, 31, 1089–1103. [Google Scholar] [CrossRef]
- Hailegeorgis, T.T.; Alfredsen, K. Regional statistical and precipitation-runoff modelling for ecological applications: prediction of hourly streamflow in regulated rivers and ungauged basins. River Res. Appl. 2016, 33, 233–248. [Google Scholar] [CrossRef] [Green Version]
- Hernandez-Ambato, J.; Asqui-Santillan, G.; Arellano, A.; Cunalata, C. Multistep-ahead Streamflow and Reservoir Level Prediction Using ANNs for Production Planning in Hydroelectric Stations. In Proceedings of the 16th IEEE International Conference on Machine Learning and Applications (ICMLA 2017), Institute of Electrical and Electronics Engineers (IEEE), Cancun, Mexico, 18–21 December 2017; pp. 479–484. [Google Scholar]
- Yaseen, Z.M.; Jaafar, O.; Deo, R.; Kisi, O.; Adamowski, J.; Quilty, J.; El-Shafie, A. Stream-flow forecasting using extreme learning machines: A case study in a semi-arid region in Iraq. J. Hydrol. 2016, 542, 603–614. [Google Scholar] [CrossRef]
- Maceira, M.E.P.; Damázio, J.M. Use of the PAR (p) model in the stochastic dual dynamic programming optimization scheme used in the operation planning of the brazilian hydropower system. Probab. Eng. Inf. Sci. 2005, 20, 143–156. [Google Scholar] [CrossRef]
- Siqueira, H.V.; Boccato, L.; Attux, R.; Lyra, C. Unorganized machines for seasonal streamflow series forecasting. Int. J. Neural Syst. 2014, 24, 1430009. [Google Scholar] [CrossRef] [PubMed]
- Munera, S.; Amigo, J.M.; Aleixos, N.; Talens, P.; Cubero, S.; Blasco, J. Potential of VIS-NIR hyperspectral imaging and chemometric methods to identify similar cultivars of nectarine. Food Control. 2018, 86, 1–10. [Google Scholar] [CrossRef]
- Yan, L.; Liu, C.; Qu, H.; Liu, W.; Zhang, Y.; Yang, J.; Zheng, L. Discrimination and measurements of three flavonols with similar structure using terahertz spectroscopy and chemometrics. J. Infrared Millim. Terahertz Waves 2018, 39, 492–504. [Google Scholar] [CrossRef]
- Moon, Y.I.; Rajagopalan, B.; Lallid, U. Estimation of mutual information using kernel density estimators. Phys. Rev. E 1995, 52, 2318–2321. [Google Scholar] [CrossRef] [PubMed]
- Crone, S.F.; Kourentzes, N. Feature selection for time series prediction—A combined filter and wrapper approach for neural networks. Neurocomputing 2010, 73, 1923–1936. [Google Scholar] [CrossRef] [Green Version]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar] [CrossRef] [Green Version]
- Wang, A.; Xie, L. Technology using near infrared spectroscopic and multivariate analysis to determine the soluble solids content of citrus fruit. J. Food Eng. 2014, 143, 17–24. [Google Scholar] [CrossRef]
- Yin, L.; Zhou, J.; Chen, D.; Han, T.; Zheng, B.; Younis, A.; Shao, Q. A review of the application of near-infrared spectroscopy to rare traditional Chinese medicine. Spectrochim. Acta Part. A Mol. Biomol. Spectrosc. 2019, 221, 117208. [Google Scholar] [CrossRef]
- Harrell, F.E. Regression Modeling Strategies; Springer Science and Business Media LLC: New York, NY, USA, 2001. [Google Scholar]
- Tsakiris, G.; Nalbantis, I.; Cavadias, G. Regionalization of low flows based on canonical correlation analysis. Adv. Water Resour. 2011, 34, 865–872. [Google Scholar] [CrossRef]
- Li, X.; Liu, Z.; Lin, H.; Wang, G.; Sun, H.; Long, J.; Zhang, M. Estimating the growing stem volume of chinese pine and larch plantations based on fused optical data using an improved variable screening method and stacking algorithm. Remote. Sens. 2020, 12, 871. [Google Scholar] [CrossRef] [Green Version]
- Bonah, E.; Huang, X.; Aheto, J.H.; Yi, R.; Yu, S.; Tu, H. Comparison of variable selection algorithms on vis-NIR hyperspectral imaging spectra for quantitative monitoring and visualization of bacterial foodborne pathogens in fresh pork muscles. Infrared Phys. Technol. 2020, 107, 103327. [Google Scholar] [CrossRef]
- Xiong, Y.; Zhang, R.; Zhang, F.; Yang, W.; Kang, Q.; Chen, W.; Du, Y. A spectra partition algorithm based on spectral clustering for interval variable selection. Infrared Phys. Technol. 2020, 105, 103259. [Google Scholar] [CrossRef]
- Speiser, J.L.; Miller, M.A.; Tooze, J.; Ip, E.H. A comparison of random forest variable selection methods for classification prediction modeling. Expert Syst. Appl. 2019, 134, 93–101. [Google Scholar] [CrossRef]
- Rendall, R.; Pereira, A.C.; Reis, M. An extended comparison study of large scale datadriven prediction methods based on variable selection, latent variables, penalized regression and machine learning. Comput. Aided Chem. Eng. 2016, 38, 1629–1634. [Google Scholar] [CrossRef]
- Marcjasz, G.; Uniejewski, B.; Weron, R. Beating the naïve—Combining LASSO with naïve intraday electricity price forecasts. Energies 2020, 13, 1667. [Google Scholar] [CrossRef] [Green Version]
- Santi, V.M.A.; Notodiputro, K.; Sartono, B. Variable selection methods applied to the mathematics scores of Indonesian students based on convex penalized likelihood. J. Phys. Conf. Ser. 2019, 1402, 077096. [Google Scholar] [CrossRef]
- Karim, N.; Reid, C.M.; Tran, L.; Cochrane, A.; Billah, B. Variable selection methods for multiple regressions influence the parsimony of risk prediction models for cardiac surgery. J. Thorac. Cardiovasc. Surg. 2017, 153, 1128–1135.e3. [Google Scholar] [CrossRef]
- Kim, D.; Kang, S. Effect of irrelevant variables on faulty wafer detection in semiconductor manufacturing. Energies 2019, 12, 2530. [Google Scholar] [CrossRef] [Green Version]
- Furmańczyk, K.; Rejchel, W. Prediction and variable selection in high-dimensional misspecified binary classification. Entropy 2020, 22, 543. [Google Scholar] [CrossRef]
- Tutkun, N.A.; Atilgan, Y.K. Visual research on the trustability of classical variable selection methods in Cox regression. Hacet. J. Math. Stat. 2020, 49, 1–18. [Google Scholar] [CrossRef]
- Mehmood, T.; Saebø, S.; Liland, K.H. Comparison of variable selection methods in partial least squares regression. J. Chemom. 2020, 34, e3226. [Google Scholar] [CrossRef] [Green Version]
- McGee, M.; Yaffee, R.A. Comparison of Variable Selection Methods for Forecasting from Short Time Series. In Proceedings of the 6th IEEE International Conference on Data Science and Advanced Analytics (DSAA 2019), Institute of Electrical and Electronics Engineers (IEEE), Washington, DC, USA, 5–8 October 2019; pp. 531–540. [Google Scholar]
- Seo, H.S. Unified methods for variable selection and outlier detection in a linear regression. Commun. Stat. Appl. Methods 2019, 26, 575–582. [Google Scholar] [CrossRef]
- Dong, W.; Yang, Q.; Fang, X. Multi-Step ahead wind power generation prediction based on hybrid machine learning techniques. Energies 2018, 11, 1975. [Google Scholar] [CrossRef] [Green Version]
- Sigauke, C.; Nemukula, M.M.; Maposa, D. Probabilistic hourly load forecasting using additive quantile regression models. Energies 2018, 11, 2208. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Sun, J.; Sun, J.; Wang, J. Using random forests to select optimal input variables for short-term wind speed forecasting models. Energies 2017, 10, 1522. [Google Scholar] [CrossRef] [Green Version]
- Taormina, R.; Ahmadi, M.H. Data-driven input variable selection for rainfall–runoff modeling using binary-coded particle swarm optimization and Extreme Learning Machines. J. Hydrol. 2015, 529, 1617–1632. [Google Scholar] [CrossRef]
- Taormina, R.; Ahmadi, M.H.; Sivakumar, B. Neural network river forecasting through baseflow separation and binary-coded swarm optimization. J. Hydrol. 2015, 529, 1788–1797. [Google Scholar] [CrossRef]
- Cui, X.; Jiang, M. Chaotic time series prediction based on binary particle swarm optimization. AASRI Proc. 2012, 1, 377–383. [Google Scholar] [CrossRef]
- Silva, N.; Siqueira, I.; Okida, S.; Stevan, S.L.; Siqueira, H.V. Neural networks for predicting prices of sugarcane derivatives. Sugar Tech. 2018, 21, 514–523. [Google Scholar] [CrossRef]
- Siqueira, H.V.; Boccato, L.; Attux, R.; Lyra, C. Echo state networks and extreme learning machines: A comparative study on seasonal streamflow series prediction. In Computer Vision; Springer Science and Business Media LLC: Heidelberg/Berlin, Germany, 2012; Volume 7664, pp. 491–500. [Google Scholar]
- Siqueira, H.V.; Boccato, L.; Attux, R.; Filho, C.L. Echo state networks for seasonal streamflow series forecasting. In Computer Vision; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2012; Volume 7435, pp. 226–236. [Google Scholar]
- Siqueira, H.V.; Boccato, L.; Attux, R.; Filho, C.L. Echo State networks in seasonal streamflow series prediction. Learn. Nonlinear Model 2012, 10, 181–191. [Google Scholar] [CrossRef] [Green Version]
- Kachba, Y.R.; Chiroli, D.M.D.G.; Belotti, J.T.; Alves, T.A.; Tadano, Y.D.S.; Siqueira, H.V. Artificial neural networks to estimate the influence of vehicular emission variables on morbidity and mortality in the largest metropolis in South America. Sustainability 2020, 12, 2621. [Google Scholar] [CrossRef] [Green Version]
- Puma-Villanueva, W.; Dos Santos, E.; Von Zuben, F. Data partition and variable selection for time series prediction using wrappers. In Proceedings of the 2006 IEEE International Joint Conference on Neural Network Proceedings, Institute of Electrical and Electronics Engineers (IEEE), Vancouver, BC, Canada, 16–21 July 2006; pp. 4740–4747. [Google Scholar]
- Yu, L.; Liu, H. Efficient feature selection via analysis of relevance and redundancy. J. Mach. Learn. Res. 2004, 5, 1205–1224. [Google Scholar]
- Hyvärinen, A.; Karhunen, J.; Oja, E. Independent Component Analysis; John Wiley and Sons: New York, NY, USA, 2001; ISBN 978-0-471-40540-5. [Google Scholar]
- Geurts, M.; Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control, 5th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2016; ISBN 978-1-118-67502-1. [Google Scholar]
- Quenouille, M.H. Approximate tests of correlation in time-series. J. R. Stat. Soc. Ser. B 1949, 11, 68–84. [Google Scholar] [CrossRef]
- Stedinger, J.R. Report on the Evaluation of CEPEL’s PAR Models, Technical Report; School of Civil and Environmental Engineering—Cornell University, Ithaca: New York, NY, USA, 2001. [Google Scholar]
- Bonnlander, V.; Weigend, A.S. Selecting Input Variables Using Mutual Information and Nonparametric Density Estimation. In Proceedings of the 1994 International Symposium on Artificial Neural Networks (ISANN’94), National Cheng Kung University, Taiwan, China, 28 June–2 July 1994; pp. 42–50. [Google Scholar]
- Luna, I.; Soares, S.; Ballini, R. Partial Mutual Information Criterion for Modelling Time Series Via Neural Networks. In Proceedings of the 11th Information Processing and Management of Uncertainty in Knowledge-Based System (IPMU 2006), Université Pierre et Marie Curie, Paris, France, 2–7 July 2006; pp. 2012–2019. [Google Scholar]
- Bowden, G.J.; Dandy, G.; Maier, H.R. Input determination for neural network models in water resources applications. Part 1—Background and methodology. J. Hydrol. 2005, 301, 75–92. [Google Scholar] [CrossRef]
- Akaho, S. Conditionally independent component analysis for supervised feature extraction. Neurocomputing 2002, 49, 139–150. [Google Scholar] [CrossRef]
- Luna, I.; Ballini, R. Top-down strategies based on adaptive fuzzy rule-based systems for daily time series forecasting. Int. J. Forecast. 2011, 27, 708–724. [Google Scholar] [CrossRef]
- Sharma, A. Seasonal to interannual rainfall probabilistic forecasts for improved water supply management: Part 1—A strategy for system predictor identification. J. Hydrol. 2000, 239, 232–239. [Google Scholar] [CrossRef]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [Green Version]
- Bowden, G.J. Forecasting Water Resources Variables Using Artificial Neural Networks. Ph.D. Thesis, University of Adelaide, Adelaide, Australia, February 2003. [Google Scholar]
- Scott, D.W. Multivariate Density Estimation: Theory, Practice, And Visualization; John Wiley and Sons: New York, NY, USA, 1992; ISBN 978-0-471-54770-9. [Google Scholar]
- Che, J.; Yang, Y.; Li, L.; Bai, X.; Zhang, S.; Deng, C.; Fowler, J.E. Maximum relevance minimum common redundancy feature selection for nonlinear data. Inf. Sci. 2017, 68–86. [Google Scholar] [CrossRef]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef] [Green Version]
- McLeod, A.I. Diagnostic checking of periodic autoregression models with application. J. Time Ser. Anal. 1994, 15, 221–233. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Institute of Electrical and Electronics Engineers (IEEE), Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Santana, C.J.; Macedo, M.; Siqueira, H.V.; Gokhale, A.A.; Bastos-Filho, C.J.A. A novel binary artificial bee colony algorithm. Futur. Gener. Comput. Syst. 2019, 98, 180–196. [Google Scholar] [CrossRef]
- Siqueira, H.; Santana, C.; Macedo, M.; Figueiredo, E.; Gokhale, A.; Bastos-Filho, C. Simplified binary cat swarm optimization. Integr. Comput. Eng. 2020, 1–15. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence, 1st ed.; MIT Press: Cambridge, MA, USA, 1992; ISBN 978-0-262-08213-6. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics, Computational Cybernetics and Simulation, Institute of Electrical and Electronics Engineers (IEEE), Orlando, FL, USA, 12–15 October 1997; Volume 5, pp. 4104–4108. [Google Scholar]
- EPE—Energy Research Company (in Portuguese: Empresa de Pesquisa Energética). 2019; Brazilian National Energy Balance 2019 (Base Year 2012). Available online: https://www.epe.gov.br/en/publications/publications/brazilian-energy-balance (accessed on 15 May 2020).
- Sacchi, R.; Ozturk, M.C.; Principe, J.C.; Carneiro, A.A.F.M.; Da Silva, I.N. Water Inflow Forecasting using the Echo State Network: A Brazilian Case Study. In Proceedings of the 2007 International Joint Conference on Neural Networks, Institute of Electrical and Electronics Engineers (IEEE), Orlando, FL, USA, 12–17 August 2007; pp. 2403–2408. [Google Scholar]
- ONS—Electric System Operator—Brazil (in Portuguese: Operador Nacional do Sistema Elétrico). 2020. Dados Hidrológicos/Vazões. Available online: http://www.ons.org.br/Paginas/resultados-da-operacao/historico-da-operacao/dados_hidrologicos_vazoes.aspx (accessed on 1 May 2020).
- Vecchia, A.V. Maximum likelihood estimation for periodic autoregressive moving average models. Technometrics 1985, 27, 375–384. [Google Scholar] [CrossRef]
- Hipel, K.W.; McLeod, A.I. Time Series Modelling of Water Resources and Environmental Systems, 1st ed.; Elsevier: New York, NY, USA, 1994; ISBN 978-0-444-89270-6. [Google Scholar]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Bartlett, P.L. The sample complexity of pattern classification with neural networks: The size of the weights is more important than the size of the network. IEEE Trans. Inf. Theory 1998, 44, 525–536. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.; Huang, G.B.; Song, S.; You, K. Trends in extreme learning machines: A review. Neural Netw. 2015, 61, 32–48. [Google Scholar] [CrossRef]
- Siqueira, H.; Luna, I. Performance comparison of feedforward neural networks applied to stream flow series forecasting. Math. Eng. Sci. Aerosp. 2019, 10, 41–53. [Google Scholar]
- Kowalczyk-Juśko, A.; Pochwatka, P.; Zaborowicz, M.; Czekała, W.; Mazurkiewicz, J.; Mazur, A.; Janczak, D.; Marczuk, A.; Dach, J. Energy value estimation of silages for substrate in biogas plants using an artificial neural network. Energy 2020, 202, 117729. [Google Scholar] [CrossRef]










| Subsets | Selected Inputs |
|---|---|
| 1 | v1 |
| 2 | v2 |
| 3 | v3 |
| 4 | v1,v2 |
| 5 | v1,v3 |
| 6 | v2,v3 |
| 7 | v1,v2,v3 |
| Complete Series | Test Set | |||
|---|---|---|---|---|
| Series | Mean (m³/s) | S. Deviation (m³/s) | Mean (m³/s) | S. Deviation (m³/s) |
| Furnas | 912.1225 | 613.5036 | 803.6833 | 611.6814 |
| Emborcação | 480.6578 | 360.3957 | 447.7333 | 355.7428 |
| Sobradinho | 2.6062 × 103 | 1.9412 × 103 | 1.9607 × 103 | 1.5001 × 103 |
| Agua Vermelha | 2.0773 × 103 | 1.2957 × 103 | 1.9635 × 103 | 1.2668 × 103 |
| Passo Real | 208.6216 | 169.7734 | 228.0083 | 167.1326 |
| Variable Selection | Test | Training | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MSE | MAE | MSEd | MAEd | MSE | MAE | MSEd | MAEd | |||
| FURNAS | WR | BIC | 109,014 | 210.77 | 0.4330 | 0.5078 | 96,033 | 196.58 | 0.4490 | 0.4907 |
| AIC | 109,014 | 210.77 | 0.4330 | 0.5078 | 96,033 | 196.58 | 0.4490 | 0.4907 | ||
| WRAPPER-MSE | 107,962 | 208.81 | 0.4224 | 0.4992 | 97,037 | 195.55 | 0.4459 | 0.4859 | ||
| Lf | FACPPe | 107,551 | 209.32 | 0.4259 | 0.5043 | 96,646 | 195.75 | 0.4464 | 0.4871 | |
| FACPPe-Sted. | 107,551 | 209.32 | 0.4259 | 0.5043 | 96,646 | 195.75 | 0.4464 | 0.4871 | ||
| Nf | MI | 108,083 | 209.65 | 0.4252 | 0.5015 | 96,702 | 195.43 | 0.4452 | 0.4856 | |
| PMI | 108,083 | 209.65 | 0.4252 | 0.5015 | 96,702 | 195.43 | 0.4452 | 0.4856 | ||
| N-MRMCR-MI | 108,083 | 209.65 | 0.4252 | 0.5015 | 96,702 | 195.43 | 0.4452 | 0.4856 | ||
| M | GA | 107,962 | 208.81 | 0.4224 | 0.4992 | 97,037 | 195.55 | 0.4459 | 0.4859 | |
| PSO | 107,962 | 208.81 | 0.4224 | 0.4992 | 97,037 | 195.55 | 0.4459 | 0.4859 | ||
| EMBORCAÇÃO | WR | BIC | 51,745 | 139.36 | 0.5487 | 0.5716 | 40,456 | 119.79 | 0.4838 | 0.5131 |
| AIC | 51,745 | 139.36 | 0.5487 | 0.5716 | 40,456 | 119.79 | 0.4838 | 0.5131 | ||
| WRAPPER-MSE | 51,745 | 139.36 | 0.5487 | 0.5716 | 40,456 | 119.79 | 0.4838 | 0.5131 | ||
| Lf | FACPPe | 50,408 | 138.01 | 0.5353 | 0.5613 | 39,953 | 119.40 | 0.4790 | 0.5102 | |
| FACPPe-Sted. | 50,408 | 138.01 | 0.5353 | 0.5613 | 39,953 | 119.40 | 0.4790 | 0.5102 | ||
| Nf | MI | 50,559 | 138.24 | 0.5397 | 0.5602 | 39,880 | 119.20 | 0.4768 | 0.5081 | |
| PMI | 50,559 | 138.24 | 0.5397 | 0.5602 | 39,880 | 119.20 | 0.4768 | 0.5081 | ||
| N-MRMCR-MI | 50,559 | 138.24 | 0.5397 | 0.5602 | 39,880 | 119.20 | 0.4768 | 0.5081 | ||
| M | GA | 51,745 | 139.36 | 0.5487 | 0.5716 | 40,456 | 119.79 | 0.4838 | 0.5131 | |
| PSO | 51,745 | 139.36 | 0.5487 | 0.5716 | 40,456 | 119.79 | 0.4838 | 0.5131 | ||
| SOBRADINHO | WR | BIC | 836,738 | 568.04 | 0.3071 | 0.4408 | 1,032,181 | 580.83 | 0.3895 | 0.4366 |
| AIC | 836,738 | 568.04 | 0.3071 | 0.4408 | 1,032,181 | 580.83 | 0.3895 | 0.4366 | ||
| WRAPPER-MSE | 836,738 | 568.04 | 0.3071 | 0.4408 | 1,032,181 | 580.83 | 0.3895 | 0.4366 | ||
| Lf | FACPPe | 836,738 | 568.04 | 0.3071 | 0.4408 | 1,032,181 | 580.83 | 0.3895 | 0.4366 | |
| FACPPe-Sted. | 863,796 | 577.30 | 0.3196 | 0.4515 | 1,020,492 | 578.13 | 0.3910 | 0.4403 | ||
| Nf | MI | 828,142 | 566.45 | 0.3043 | 0.4375 | 994,408 | 573.77 | 0.3837 | 0.4350 | |
| PMI | 828,142 | 566.45 | 0.3043 | 0.4375 | 994,408 | 573.77 | 0.3837 | 0.4350 | ||
| N-MRMCR-MI | 828,142 | 566.45 | 0.3043 | 0.4375 | 994,408 | 573.77 | 0.3837 | 0.4350 | ||
| M | GA | 836,738 | 568.04 | 0.3071 | 0.4408 | 1,032,181 | 580.83 | 0.3895 | 0.4366 | |
| PSO | 836,738 | 568.04 | 0.3071 | 0.4408 | 1,032,181 | 580.83 | 0.3895 | 0.4366 | ||
| AGUA VERMELHA | WR | BIC | 417,720 | 404.35 | 0.4097 | 0.4826 | 378,866 | 394.30 | 0.4095 | 0.4780 |
| AIC | 417,720 | 404.35 | 0.4097 | 0.4826 | 378,866 | 394.30 | 0.4095 | 0.4780 | ||
| WRAPPER-MSE | 417,720 | 404.35 | 0.4097 | 0.4826 | 378,866 | 394.30 | 0.4095 | 0.4780 | ||
| Lf | FACPPe | 409,613 | 401.00 | 0.4052 | 0.4803 | 379,329 | 392.98 | 0.4078 | 0.4752 | |
| FACPPe-Sted. | 409,613 | 401.00 | 0.4052 | 0.4803 | 379,329 | 392.98 | 0.4078 | 0.4752 | ||
| Nf | MI | 415,465 | 404.50 | 0.4062 | 0.4828 | 378,197 | 392.12 | 0.4065 | 0.4749 | |
| PMI | 413,991 | 403.40 | 0.4119 | 0.4886 | 369,658 | 393.50 | 0.4149 | 0.4819 | ||
| N-MRMCR-MI | 413,991 | 403.40 | 0.4119 | 0.4886 | 378,197 | 392.12 | 0.4065 | 0.4749 | ||
| M | GA | 415,465 | 404.50 | 0.4062 | 0.4828 | 378,197 | 392.12 | 0.4065 | 0.4749 | |
| PSO | 415,465 | 404.50 | 0.4062 | 0.4828 | 378,197 | 392.12 | 0.4065 | 0.4749 | ||
| PASSO REAL | WR | BIC | 14,996 | 88.65 | 0.6570 | 0.5969 | 16,637 | 86.70 | 0.6490 | 0.5718 |
| AIC | 14,996 | 88.65 | 0.6570 | 0.5969 | 16,637 | 86.70 | 0.6490 | 0.5718 | ||
| WRAPPER-MSE | 14,996 | 88.65 | 0.6570 | 0.5969 | 16,637 | 86.70 | 0.6490 | 0.5718 | ||
| Lf | FACPPe | 14,523 | 87.74 | 0.6397 | 0.5914 | 16,497 | 86.32 | 0.6415 | 0.5696 | |
| FACPPe-Sted. | 14,523 | 87.74 | 0.6397 | 0.5914 | 16,497 | 86.32 | 0.6415 | 0.5696 | ||
| Nf | MI | 14,632 | 88.16 | 0.6447 | 0.5956 | 16,478 | 86.08 | 0.6398 | 0.5676 | |
| PMI | 14,632 | 88.16 | 0.6447 | 0.5956 | 16,478 | 86.08 | 0.6398 | 0.5676 | ||
| N-MRMCR-MI | 14,632 | 88.16 | 0.6447 | 0.5956 | 16,478 | 86.08 | 0.6398 | 0.5676 | ||
| M | GA | 14,996 | 88.65 | 0.6570 | 0.5969 | 16,637 | 86.70 | 0.6490 | 0.5718 | |
| PSO | 14,996 | 88.65 | 0.6570 | 0.5969 | 16,637 | 86.70 | 0.6490 | 0.5718 | ||
| Variable Selection | Test | Training | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MSE | MAE | MSEd | MAEd | MSE | MAE | MSEd | MAEd | |||
| FURNAS | WR | BIC | 117,347 | 207.37 | 0.4096 | 0.4819 | 94,879 | 190.77 | 0.4124 | 0.4725 |
| AIC | 120,629 | 211.50 | 0.4343 | 0.4957 | 93,403 | 189.09 | 0.4041 | 0.4677 | ||
| WRAPPER-MSE | 128,415 | 215.49 | 0.4546 | 0.5046 | 87,842 | 183.45 | 0.3846 | 0.4556 | ||
| Lf | PACF | 118,744 | 211.52 | 0.4113 | 0.4882 | 102,317 | 198.26 | 0.4499 | 0.4899 | |
| PACF-Sted. | 117,144 | 206.70 | 0.4055 | 0.4788 | 94,824 | 190.41 | 0.4112 | 0.4709 | ||
| Nf | MI | 120,121 | 211.57 | 0.4302 | 0.4963 | 92,821 | 187.35 | 0.3973 | 0.4620 | |
| PMI | 122,682 | 215.72 | 0.4442 | 0.5055 | 96,930 | 193.12 | 0.4502 | 0.4822 | ||
| N-MRMCR-MI | 135,260 | 224.64 | 0.4811 | 0.5271 | 95,500 | 187.39 | 0.3999 | 0.4619 | ||
| M | GA | 128,680 | 216.09 | 0.4601 | 0.5073 | 87,837 | 183.33 | 0.3845 | 0.4550 | |
| PSO | 133,171 | 228.39 | 0.4794 | 0.5279 | 109,291 | 201.15 | 0.4856 | 0.5007 | ||
| EMBORCAÇÃO | WR | BIC | 46,356 | 128.98 | 0.5034 | 0.5350 | 35,421 | 112.66 | 0.4377 | 0.4817 |
| AIC | 46,356 | 129.00 | 0.5034 | 0.5352 | 35,415 | 112.57 | 0.4370 | 0.4806 | ||
| WRAPPER-MSE | 51,529 | 134.64 | 0.5460 | 0.5489 | 33,362 | 109.12 | 0.4188 | 0.4702 | ||
| Lf | PACF | 50,251 | 134.96 | 0.5526 | 0.5612 | 42,622 | 123.54 | 0.5596 | 0.5418 | |
| PACF-Sted. | 46,195 | 129.23 | 0.5093 | 0.5444 | 35,710 | 113.81 | 0.4535 | 0.4914 | ||
| Nf | MI | 47,918 | 130.25 | 0.5094 | 0.5353 | 39,096 | 115.99 | 0.4588 | 0.4851 | |
| PMI | 48,392 | 129.72 | 0.5183 | 0.5361 | 40,967 | 118.63 | 0.4913 | 0.5010 | ||
| N-MRMCR-MI | 46,088 | 128.22 | 0.4982 | 0.5343 | 35,593 | 113.05 | 0.4419 | 0.4836 | ||
| M | GA | 51,529 | 134.64 | 0.5460 | 0.5489 | 33,362 | 109.12 | 0.4188 | 0.4702 | |
| PSO | 58,768 | 153.16 | 0.9161 | 0.6795 | 48,079 | 136.61 | 0.8187 | 0.6266 | ||
| SOBRADINHO | WR | BIC | 650,374 | 507.00 | 0.2791 | 0.4097 | 850,140 | 530.47 | 0.3560 | 0.4133 |
| AIC | 642,631 | 496.61 | 0.2706 | 0.3972 | 847,763 | 528.97 | 0.3530 | 0.4118 | ||
| WRAPPER-MSE | 675,439 | 510.13 | 0.3071 | 0.4194 | 829,497 | 523.19 | 0.3450 | 0.4061 | ||
| Lf | PACF | 724,099 | 546.38 | 0.3361 | 0.4462 | 1,021,024 | 577.88 | 0.4665 | 0.4523 | |
| PACF-Sted. | 666,690 | 513.82 | 0.2896 | 0.4175 | 886,340 | 540.87 | 0.3671 | 0.4207 | ||
| Nf | MI | 628,672 | 495.94 | 0.2923 | 0.4124 | 847,892 | 530.37 | 0.3519 | 0.4104 | |
| PMI | 665,958 | 511.55 | 0.2948 | 0.4171 | 886,511 | 544.87 | 0.3852 | 0.4340 | ||
| N-MRMCR-MI | 682,074 | 513.84 | 0.3034 | 0.4180 | 824,000 | 519.21 | 0.3399 | 0.4010 | ||
| M | GA | 675,494 | 510.64 | 0.3074 | 0.4207 | 829,499 | 523.20 | 0.3450 | 0.4061 | |
| PSO | 755,372 | 564.36 | 0.3402 | 0.4509 | 1,181,095 | 632.30 | 0.5290 | 0.4889 | ||
| AGUA VERMELHA | WR | BIC | 438,074 | 401.41 | 0.4075 | 0.4729 | 357,604 | 380.46 | 0.3774 | 0.4614 |
| AIC | 439,586 | 402.88 | 0.4161 | 0.4769 | 356,951 | 379.09 | 0.3742 | 0.4587 | ||
| WRAPPER-MSE | 473,968 | 409.23 | 0.4437 | 0.4881 | 335,448 | 366.74 | 0.3564 | 0.4461 | ||
| Lf | PACF | 469,836 | 407.75 | 0.4179 | 0.4732 | 404,467 | 393.70 | 0.4056 | 0.4728 | |
| PACF-Sted. | 432,799 | 393.57 | 0.3960 | 0.4611 | 359,174 | 382.19 | 0.3817 | 0.4645 | ||
| Nf | MI | 459,970 | 408.37 | 0.4300 | 0.4836 | 379,638 | 380.90 | 0.3817 | 0.4566 | |
| PMI | 443,387 | 399.30 | 0.4188 | 0.4711 | 360,565 | 384.67 | 0.3838 | 0.4673 | ||
| N-MRMCR-MI | 436,274 | 395.68 | 0.4029 | 0.4664 | 357,410 | 380.80 | 0.3781 | 0.4618 | ||
| M | GA | 476,365 | 409.64 | 0.4450 | 0.4884 | 335,047 | 366.40 | 0.3561 | 0.4459 | |
| PSO | 775,418 | 560.05 | 0.7722 | 0.6972 | 627,743 | 500.78 | 0.7843 | 0.6385 | ||
| PASSO REAL | WR | BIC | 16,793 | 93.49 | 0.7945 | 0.6449 | 15,864 | 85.70 | 0.6228 | 0.5684 |
| AIC | 15,601 | 88.50 | 0.7664 | 0.6198 | 15,299 | 84.28 | 0.6022 | 0.5590 | ||
| WRAPPER-MSE | 15,584 | 91.70 | 0.7454 | 0.6395 | 14,770 | 82.82 | 0.5797 | 0.5474 | ||
| Lf | PACF | 15,924 | 90.39 | 0.8031 | 0.6296 | 15,012 | 84.05 | 0.6062 | 0.5605 | |
| PACF-Sted. | 15,522 | 89.04 | 0.7557 | 0.6151 | 14,976 | 83.78 | 0.6018 | 0.5576 | ||
| Nf | MI | 14,982 | 90.73 | 0.7152 | 0.6300 | 16,107 | 85.61 | 0.6336 | 0.5671 | |
| PMI | 15,282 | 87.41 | 0.7423 | 0.6038 | 16,013 | 85.63 | 0.6344 | 0.564 | ||
| N-MRMCR-MI | 15,474 | 90.55 | 0.7402 | 0.6306 | 14,638 | 82.25 | 0.5724 | 0.5428 | ||
| M | GA | 15,779 | 92.12 | 0.7551 | 0.6424 | 14,769 | 82.99 | 0.5796 | 0.5486 | |
| PSO | 17,895 | 101.47 | 0.8774 | 0.7130 | 22,018 | 103.18 | 0.8769 | 0.6816 | ||
| Variable Selection | Monthly Approach | Annual Approach | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MSE | MAE | MSEd | MAEd | MSE | MAE | MSEd | MAEd | |||
| FURNAS | WR | BIC | 124,391 | 212.47 | 0.4320 | 0.4943 | 123,754 | 220.19 | 0.4597 | 0.5307 |
| AIC | 123,550 | 210.02 | 0.4264 | 0.4878 | 126,426 | 219.67 | 0.4503 | 0.5195 | ||
| WRAPPER-MSE | 119,067 | 206.45 | 0.4060 | 0.4809 | 123,745 | 217.80 | 0.4455 | 0.5171 | ||
| Lf | PACF | 126,594 | 222.32 | 0.4623 | 0.5236 | 129,323 | 219.72 | 0.4451 | 0.5138 | |
| PACF-Sted. | 121,806 | 212.11 | 0.4433 | 0.4997 | 126,768 | 216.79 | 0.4509 | 0.5110 | ||
| Nf | MI | 130,637 | 230.24 | 0.5115 | 0.5656 | 124,105 | 220.33 | 0.4665 | 0.5279 | |
| PMI | 126,445 | 217.60 | 0.4769 | 0.5207 | 126,349 | 221.97 | 0.4611 | 0.5287 | ||
| N-MRMCR-MI | 140,451 | 238.15 | 0.5424 | 0.5842 | 126,507 | 222.67 | 0.4650 | 0.5330 | ||
| M | GA | 137,304 | 230.58 | 0.5063 | 0.5448 | 135,978 | 232.35 | 0.4963 | 0.5594 | |
| PSO | 132,599 | 228.87 | 0.4829 | 0.5377 | 131,426 | 226.52 | 0.4823 | 0.5435 | ||
| EMBORCAÇÃO | WR | BIC | 38,143 | 114.51 | 0.4495 | 0.4956 | 48,513 | 130.03 | 0.5333 | 0.5586 |
| AIC | 41,110 | 116.21 | 0.4657 | 0.4944 | 45,459 | 127.26 | 0.5158 | 0.5501 | ||
| WRAPPER-MSE | 37,551 | 118.56 | 0.4335 | 0.5001 | 44,936 | 129.15 | 0.5137 | 0.5557 | ||
| Lf | PACF | 44,227 | 124.36 | 0.5122 | 0.5355 | 45,994 | 130.15 | 0.5153 | 0.5563 | |
| PACF-Sted. | 48,543 | 130.42 | 0.5395 | 0.5526 | 44,690 | 129.01 | 0.5095 | 0.5556 | ||
| Nf | MI | 49,315 | 131.44 | 0.5641 | 0.5662 | 45,169 | 130.89 | 0.5126 | 0.5565 | |
| PMI | 52,571 | 132.20 | 0.5707 | 0.5564 | 44,094 | 128.54 | 0.5061 | 0.5511 | ||
| N-MRMCR-MI | 47,931 | 129.26 | 0.5398 | 0.5459 | 45,707 | 129.50 | 0.5169 | 0.5558 | ||
| M | GA | 54,659 | 142.88 | 0.6225 | 0.6017 | 45,434 | 128.47 | 0.5166 | 0.5515 | |
| PSO | 50,211 | 130.82 | 0.5667 | 0.5644 | 45,298 | 130.20 | 0.5170 | 0.5595 | ||
| SOBRADINHO | WR | BIC | 642,185 | 519.69 | 0.2954 | 0.4329 | 669,441 | 534.37 | 0.3209 | 0.4632 |
| AIC | 590,254 | 492.20 | 0.2979 | 0.4298 | 657,405 | 530.22 | 0.3166 | 0.4532 | ||
| WRAPPER-MSE | 587,680 | 495.73 | 0.2945 | 0.4250 | 672,783 | 531.90 | 0.3229 | 0.4567 | ||
| Lf | PACF | 696,480 | 530.92 | 0.3376 | 0.4506 | 718,719 | 549.40 | 0.3366 | 0.4676 | |
| PACF-Sted. | 747,932 | 550.63 | 0.3561 | 0.4591 | 690,307 | 549.76 | 0.3510 | 0.4872 | ||
| Nf | MI | 692,277 | 533.35 | 0.3526 | 0.4587 | 668,656 | 531.83 | 0.3187 | 0.4527 | |
| PMI | 746,916 | 546.82 | 0.3647 | 0.4621 | 694,596 | 540.00 | 0.3234 | 0.4549 | ||
| N-MRMCR-MI | 828,437 | 582.14 | 0.4819 | 0.3842 | 710,649 | 542.32 | 0.3316 | 0.4583 | ||
| M | GA | 728,468 | 563.81 | 0.3400 | 0.4674 | 698,381 | 555.96 | 0.3501 | 0.4869 | |
| PSO | 773,147 | 571.99 | 0.3657 | 0.4738 | 712,829 | 558.87 | 0.3655 | 0.4920 | ||
| AGUA VERMELHA | WR | BIC | 408,982 | 384.66 | 0.3646 | 0.4528 | 443,959 | 394.45 | 0.4055 | 0.4727 |
| AIC | 411,485 | 387.40 | 0.3701 | 0.4583 | 436,790 | 393.10 | 0.3946 | 0.4661 | ||
| WRAPPER-MSE | 374,264 | 375.43 | 0.3412 | 0.4429 | 436,981 | 394.69 | 0.3952 | 0.4664 | ||
| Lf | PACF | 436,494 | 412.25 | 0.4109 | 0.4864 | 439,692 | 401.17 | 0.4025 | 0.4759 | |
| PACF-Sted. | 419,472 | 401.62 | 0.4040 | 0.4813 | 458,381 | 406.68 | 0.4131 | 0.4813 | ||
| Nf | MI | 423,961 | 426.85 | 0.4565 | 0.5274 | 453,903 | 420.36 | 0.4288 | 0.5065 | |
| PMI | 434,519 | 410.82 | 0.4420 | 0.5026 | 432,417 | 394.64 | 0.3955 | 0.4687 | ||
| N-MRMCR-MI | 417,154 | 397.18 | 0.4020 | 0.4787 | 458,725 | 422.00 | 0.4344 | 0.5076 | ||
| M | GA | 502,689 | 437.62 | 0.4673 | 0.5201 | 449,919 | 405.97 | 0.4142 | 0.4874 | |
| PSO | 478,617 | 440.21 | 0.4526 | 0.5271 | 439,377 | 402.75 | 0.4022 | 0.4806 | ||
| PASSO REAL | WR | BIC | 12,768 | 79.70 | 0.6382 | 0.5549 | 15,859 | 89.78 | 0.7367 | 0.6079 |
| AIC | 12,964 | 78.81 | 0.6592 | 0.5490 | 15,866 | 89.78 | 0.7366 | 0.6078 | ||
| WRAPPER-MSE | 11,828 | 78.42 | 0.6033 | 0.5488 | 15,435 | 87.80 | 0.7277 | 0.5962 | ||
| Lf | PACF | 16,288 | 91.41 | 0.7772 | 0.6218 | 15,257 | 86.40 | 0.7278 | 0.5884 | |
| PACF-Sted. | 16,435 | 89.65 | 0.7850 | 0.6116 | 15,351 | 86.55 | 0.7320 | 0.5893 | ||
| Nf | MI | 15,059 | 86.49 | 0.7196 | 0.5944 | 16,074 | 89.96 | 0.7612 | 0.6170 | |
| PMI | 15,400 | 87.35 | 0.7517 | 0.5979 | 16,146 | 91.00 | 0.7584 | 0.6207 | ||
| N-MRMCR-MI | 16,635 | 91.48 | 0.7723 | 0.6274 | 16,208 | 90.10 | 0.7683 | 0.6168 | ||
| M | GA | 17,035 | 90.31 | 0.8134 | 0.6140 | 16,258 | 91.15 | 0.7626 | 0.6206 | |
| PSO | 15,589 | 86.86 | 0.7344 | 0.5964 | 16,270 | 91.04 | 0.7731 | 0.6217 | ||
| Models | ||||||
|---|---|---|---|---|---|---|
| VS Method | AR Train | AR Test | PAR Train | PAR Test | ELM Annual | ELM Monthly |
| BIC | 1(+1) | - | - | - | 1(+3) | - |
| AIC | 1(+1) | - | - | - | 2; 1(+8) | - |
| WRAPPER-MSE | - | - | 1(+1) | - | 1(+3); 1(+8) | 5 |
| PACF | - | 1(+1); 1(+1); 1(+1); 1(+1) | - | - | 1; 1(+8) | - |
| PACF-Sted. | - | 1(+1); 1(+1); 1(+1); 1(+1) | - | 2 | 1(+8) | - |
| MI | 1(+2); 1(+2); 1(+2) | 1(+2) | - | 2 | 1(+3); 1(+8) | - |
| PMI | 1; 1(+2); 1(+2); 1(+2) | 1(+2) | - | - | 1(+3); 1(+8) | - |
| N-MRMCR-MI | 1(+2); 1(+2); 1(+2) | 1(+2) | 1 | 1 | 1(+8) | - |
| GA | - | - | 3; 1(+1) | - | 1(+8) | - |
| PSO | - | - | - | - | 1(+8) | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siqueira, H.; Macedo, M.; Tadano, Y.d.S.; Alves, T.A.; Stevan, S.L., Jr.; Oliveira, D.S., Jr.; Marinho, M.H.N.; Neto, P.S.G.d.M.; Oliveira, .F.L.d.; Luna, I.; et al. Selection of Temporal Lags for Predicting Riverflow Series from Hydroelectric Plants Using Variable Selection Methods. Energies 2020, 13, 4236. https://doi.org/10.3390/en13164236
Siqueira H, Macedo M, Tadano YdS, Alves TA, Stevan SL Jr., Oliveira DS Jr., Marinho MHN, Neto PSGdM, Oliveira FLd, Luna I, et al. Selection of Temporal Lags for Predicting Riverflow Series from Hydroelectric Plants Using Variable Selection Methods. Energies. 2020; 13(16):4236. https://doi.org/10.3390/en13164236
Chicago/Turabian StyleSiqueira, Hugo, Mariana Macedo, Yara de Souza Tadano, Thiago Antonini Alves, Sergio L. Stevan, Jr., Domingos S. Oliveira, Jr., Manoel H.N. Marinho, Paulo S.G. de Mattos Neto, João F. L. de Oliveira, Ivette Luna, and et al. 2020. "Selection of Temporal Lags for Predicting Riverflow Series from Hydroelectric Plants Using Variable Selection Methods" Energies 13, no. 16: 4236. https://doi.org/10.3390/en13164236
APA StyleSiqueira, H., Macedo, M., Tadano, Y. d. S., Alves, T. A., Stevan, S. L., Jr., Oliveira, D. S., Jr., Marinho, M. H. N., Neto, P. S. G. d. M., Oliveira, . F. L. d., Luna, I., Filho, M. d. A. L., Sarubbo, L. A., & Converti, A. (2020). Selection of Temporal Lags for Predicting Riverflow Series from Hydroelectric Plants Using Variable Selection Methods. Energies, 13(16), 4236. https://doi.org/10.3390/en13164236