Energy Analyses of Serbian Buildings with Horizontal Overhangs: A Case Study

Abstract

It is well known that nowadays a significant part of the total energy consumption is related to buildings, so research for improving building energy efficiency is very important. This paper presents our investigations about the dimensioning of horizontal overhangs in order to determine the minimum annual consumption of building primary energy for heating, cooling and lighting. In this investigation, embodied energy for horizontal roof overhangs was taken into account. The annual simulation was carried out for a residential building located in the city of Belgrade (Serbia). Horizontal overhangs (roof and balcony) are positioned to provide shading of all exterior of the building. The building is simulated in the EnergyPlus software environment. The optimization of the overhang size was performed by using the Hooke Jeeves algorithm and plug-in GenOpt program. The objective function minimizes the annual consumption of primary energy for heating, cooling and lighting of the building and energy spent to build overhangs. The simulation results show that the building with optimally sized roof and balcony overhangs consumed 7.12% lessprimary energy for heating, cooling and lighting, compared to the house without overhangs. A 44.15% reduction in cooling energy consumption is also achieved.

1. Introduction

Reduction in energy consumption is globally of great importance as the combustion of fossil fuels emits significant amounts of greenhouse gases, primarily carbon dioxide. Fossil fuels are also a limited resource which isdecreasing in Nature and should be very cautiously used. In order to reduce the primary energy consumption, it is essential to focus on reducing energy consumption in buildings. Building energy consumption is related to the exploitation conditions, where the largest consumers are the heating, cooling and domestic hot water systems, appliances, etc. Reducing energy consumption can be achieved by the construction of energy efficient buildings which have lower total energy consumption and lower greenhouse gas emissions. It is very important to apply as many measures to design energy efficient buildings as possible, primarily in the passive design of buildings. An application of passive energy elements on buildings, which include elements of shading by horizontal roof overhangs improves thermal indoor comfort, reduces primary energy consumption and hence reduces greenhouse gas emissions. Sometimes, a building design strives to insulate the building from outside influences, and thus to reduce energy exchange. At the other hand, it is necessary to utilize energy from the environment in the best way in order to achieve even better results. The implementation of these principles at the building design stage is the most effective way to achieve good results in the reduction of the energy required for heating, cooling, and lighting.

Many studies were carried out to analyze the impact of shading elements to energy consumption and most authors found a reduction in energy consumption for cooling due to shadowing. Cooling load due to solar gain represents about half of the total cooling load of residential buildings [1]. Solar radiation through the building windows can be decreased with different shading devices installed on the exterior side of building windows [2]. Skias and Kolokotsa analyzed the office building energy consumption for cooling in Athens (Greece) and ways of reducing it during the summer period by placing shadowing elements [3]. Their investigation was carried out in TRNSYS 16, and the application of the horizontal roof overhangs on the south side of the building yielded building energy savingsthat ranged from 7.2% to 17.5%. Kim et al. studied energy saving for cooling with the IES_VE program for a shaded building located in South Korea [4]. They found that by building with horizontal overhangs on the south façade, it is possible to achieve energy savings for cooling of 11%. Raeissi and Taheri investigated the energy consumption for heating and cooling in a family home with horizontal roof overhangs located in Shiraz (Iran), at an altitude of 1491 m [5]. Analyses were performed for cooling and heating periods. The optimization of the primary energy consumption for building cooling and heating achieved a reduction in energy consumption for cooling by 12.7% and increased the energy consumption for heating by 0.63%. Bojic at al. in their paper [1] analyzed the primary energy consumption in residential building with overhangs during the summer season. The obtained results showed that in the case of a house without optimized overhangs, there is an increase in primary energy consumptionby 3.36% and in that case, the operative energy consumption is lower. Imessad at al. investigated a building with horizontal overhangs, located in Algiers, where there is a temperate Mediterranean climate [6]. This analysis was carried out in TRNSYS software, and results showed that horizontal overhangs in combination with natural ventilation can and improve thermal comfort and reduce cooling energy demand in the summer periodby 35%. Datta in his study [7] analyzed building with external fixed shading device for windows, in different cities in Italy (north to south). With a simulation model in the TRNSYS program, he optimized shading device size with the aim to minimize annual primary energy consumption in buildings. The results showed that with optimum shading a 70% solar gain can be avoided in Milan during the summer season. An air-conditioned office in England with fixed external overhang was investigated with simulations in the DOE-2 modeling program [8]. The obtained results showed that energy savings depend on latitude, so in Scotland it was between 1% and 9%. With moveable external shading the highest energy savings can be achieved. Yao [9] simulated a high residential building in Ningbo, China, which has movable solar shading devices in south-facing rooms, in the EnergyPlus software. The simulation results showed that movable solar shading devices can reduce building energy consumption by 30.87% and improve visual comfort for about 20%. Atzeri et al. [10] in their paper investigated an open-space office located in Rome (Italy). They used the EnergyPlus software, and compared the influence of indoor and outdoor shading devices on primary energy consumption, thermal and visual comfort. The main conclusion was that external shading devices can reduce cooling needs and increased heating load. Florides at al. [11] modeled and simulated a modern building with the aim to reduce its thermal load. They recommended a window overhang length of 1.5 m, with which it is possible to save 7% of annual cooling energy consumption for a building with single walls and without roof insulation, and 19% of annual cooling energy consumption for the buildings with walls and roof with 50 mm insulation [11]. Liu et al. [12] investigated shading devices on opaque facades of public buildings in Hong Kong and the possibilities for energy savings with them. They varied the length, the number and the tilt angle of the different configurations of shading devices and found optimal values for west-oriented overhangs, with an energy saving potential of up to 8%.

Aldawoud simulated the energy behavior of an office building with external shading devices and electrochromic glazed windows, located in Phoenix, a city in Arizona, USA, which has a very hot and dry climate. Simulations were carried out in the Design Builder software. Among the other energy performance factors, great attention was paid to the energy consumption for heating, cooling and interior lighting. The simulation results showed that electrochromic glazing provided the greatest reduction of solar heat gains during hot summer days. Also, well-designed overhangs allow a significant reduction in cooling load [13].

Mandalaki et al. [14] analyzed the energy needed for heating, cooling and lighting for office rooms with shading devices, located in the cities of Athens and Chania (Greece). The aim of the analyses was to determine the optimal size of shading devices with integrated south-facing PV panels, which generate electricity for lighting. The results showed that shading devices decrease the building energy consumption. Stamatakis et al. applied multi-criteria analyses of monocrystalline PV panels mounted on south-facing shading devices on office buildings in the Mediterranean region [15]. A novel design of energy-efficient shading devices with amorphous panels was investigated by parametric modeling [16]. Objective functions were the minimal value of total energy consumption and useful daylight illuminance. The achieved savings in total building energy consumption was 14%, with a daylight level above 50%.

Bellia et al. have provided an overview of lighting analysis, energy analysis, HVAC system energy requirements and comprehensive analyses of thermal, visual and energetic aspects for buildings with fixed, movable and others shading systems [17]. Also, a review of simulation modeling for different type of shading devices which are implemented in modern buildings today was given by Kirmtat et al. [18]. The effects of horizontal and vertical louver shading devices, applied to different building façades at different locations, on building energy consumption are analyzed in [19] using the TRNSYS software. Obtained results showed significant energy savings in comparison to a building without shading devices. Valladares-Rendón et al. investigated solar protection and building energy saving in buildings with balanced daylighting and visibility and optimal orientation for façade shading systems [20]. The investigated buildings were in the subtropical zone, at 59 different locations. The results showed that passive strategies can reduce energy consumption by 4.64% to 76.57%. Numerical simulations showed that 58.62% of the locations should apply east oriented, 24.13% northeast oriented, 12.06% west oriented and 5.17%southeast oriented optimal designs. Al-Masarni and Al-Obaidi theoretically and experimentally analyzed current applications and trends of dynamic shading systems [21]. Their outcomes give a classification of shading models and analysis of their performance, with some recommendations for improving dynamic shading systems’ performance, which can be very useful for architects. Tabadkani et al. reviewed studies with automatic shading control methods for balancing comfort and energy savings in buildings [22]. They concluded that existing studies investigated only automatic shading controls such as roller shades or venetian blinds, which can contribute to the reduction of energy consumption.

Serbia is among the countries that has the lowest level of energy efficiency in Europe and is therefore located at the bottom of the list of energy-efficient countries. This information is fully illustrated by the fact that in Serbia there are an estimated 300,000–400,000 energy-inefficient residential buildings (single family houses) which have no thermal insulation and with an annual final energy consumption of 220 kWh/m² [23], while the European annualenergy consumption ranges from 55 kWh/m² in Malta and 70 kWh/m² in Portugal, to 300 kWh/m² in Romania [24].

Energy consumption in buildings at the global level is 20–40% of total energy consumption, while in Serbia it is at the 35%level [25]. This energy consumption is related to the exploitation conditions of buildings. In the structures of total energy consumption of Serbian building, about 60% of the energy consumption is related to the space heating [23], or approximately 65 million MWh per annum [26]. About 76% of this consumption pertains to single family houses and 24% to multifamily houses [26].

Residential buildings represent the biggest part of national building stock of Serbia, and more than 90% of them are single family houses. Most of these residential buildings (58.78%) are older buildings that were built in the 1960s, 1970s and 1980s, and are characterized by excessive energy consumption, due to the absence or poor thermal insulation, whether due to inefficient doors and windows, etc. In accordance with the national residential buildings typology in Serbia, these buildings belong to the groups D1, E1 and F1 [26], and they are usually two-storey, free standing, single family buildings. In the last 20 years, some basic energy-saving measures have been implemented in these buildings in order to improve their energy efficiency—application of thermal insulation on the external walls, roof and floors, replacement the old inefficient windows, doors, etc. In that way, a certain energy savings is achieved, but, it is also necessary to implement some other measures and find other ways for minimizing building energy consumption, especially for heating and cooling.

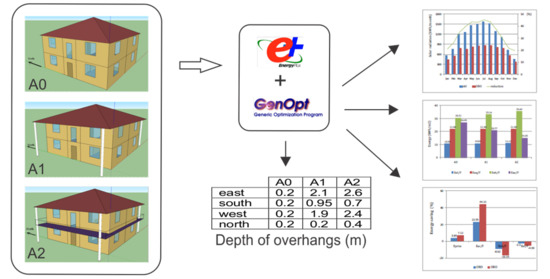
In the literature, there is almost no investigation of how the installation of overhangs influences the common consumption of energy for heating, cooling and lighting in Serbian buildings. This paper reports numerical investigations about how shading by horizontal roof and balcony overhangs influences the primary and final energy consumption for heating, cooling and lighting of residential buildings in Serbia through the year. Analyzed buildings are modeled in accordance with the national residential buildings typology in Serbia, and they represent typical buildings which were built in the period from 1960 until 1990, with thermal insulation on the external walls and energy-efficient windows. In this paper, optimal size of the horizontal roof overhangs, which are placed over east, west, north, and south wall, are obtained by simultaneous operation of the two programs EnergyPlus and GenOpt. The optimization is performed to minimize the primary energy consumption for heating, cooling and lighting. In these processes, the embodied energy of concrete horizontal roof overhangs was taken into account [27].

The primary energy saving and cooling energy consumption results obtained with numerical simulations and optimizations are within the frame of research results of the other authors who have conducted similar studies, but in some other regions of Europe. Serbia lies in the central part of the Balkan Peninsula, and has a moderate continental climate, characterized by cold winters, warm summers, and well-distributed rainfall, like in the other northern and central parts of the Balkans. The results of this study are not merely useful for the study of the methods for improving building energy efficiency aimed at optimizing overhangs and minimizing of Serbian building energy consumption, but above all, they could represent useful information for similar studies conducted in other parts of Europe that share the same or similar characteristics in terms of climate and topography.

2. Materials and Methods

2.1. Description of Modeled Buildings

In this research, the energy consumption is investigated for three buildings shown in Figure 1 as models in the EnergyPlus software [28]. These buildings are detached with two-floors. They have almost the same characteristics.

They only differ in their overhang characteristics such as type and dimensions. They were: (1) a basic building, (2) a building with optimized roof overhangs (ORO building), and (3) a building with optimized balcony overhangs (OBO building). Two types of overhangs were studied—roof and balcony. The roof overhangs were parts of roof that acted as overhangs for the second floor apartments. The balcony overhangs acted as overhangs for the first floor apartments and as the balconies for the second floor apartments. The basic building had roof overhangs with depths of 0.2 m. The ORO building had optimized roof overhangs. The OBO building had optimized balcony overhangs. The balcony overhangs were balconies of the second floor apartments that acted as overhangs for the first floor apartments. This building had also roof overhangs with the same depths as in the ORO building. All overhangs are thermally insulated with polystyrene (0.05 m) to avoid or minimize the appearance of thermal bridges. The cross-section of the building in Figure 1d shows the distribution of rooms on the first and second floor. Each floor has four rooms of identical size of 23 m²: kitchen, living room, bedroom 1 and bedroom 2. Each of them was air-conditioned and illuminated by an average brightness of 500 lux. Additionally, there were a toilet and corridor.

To study the impact of shadowing more in details, the influence of tenant activities in buildings is excluded, although in practice this is not situation. The overhang geometry is shown in Figure 2 for the ORO and OBO building.

Each investigated building had a total floor area of 234 m², of which F = 186 m² were cooled and heated. The constructions used in the envelope of each house are shown in

Table 1. Materials used in the envelope of the buildings.

Construction	Layers	Material	Thickness [m]	Conductivity [W/m·K]	Density [kg/m3]	Specific Heat [J/kg·K]
External wall	Outside Layer	Cementmortar	0.015	0.81	1600	1050
	Layer 2	Polystyrene	0.15	0.041	20	1260
	Layer 3	Clay block	0.19	0.52	1200	920
	Layer 4	Lime mortar	0.015	0.81	1600	1050
Inner wall	Outside Layer	Lime mortar	0.015	0.81	1600	1050
	Layer 2	Clay block	0.19	0.52	1200	920
	Layer 3	Lime mortar	0.015	0.81	1600	1050
Ceiling panel	Outside Layer	Cement screed	0.04	1.4	2100	1050
	Layer 2	Glass wool	0.08	0.04	50	840
	Layer 3	Monta block	0.16	0.6	1200	920
	Layer 4	Lime mortar	0.015	0.81	1600	1050
Floor (parquet)	Outside Layer	Sand	0.2	0.81	1700	840
	Layer 2	Concrete	0.15	0.93	1800	960
	Layer 3	PVC foil	0.00015	0.19	1460	1100
	Layer 4	Stirodure	0.05	0.03	33	1260
	Layer 5	Cement screed	0.04	1.4	2100	1050
	Layer 6	Parquet	0.02	0.21	700	1670
Floor (tiles)	Outside Layer	Sand	0.2	0.81	1700	840
	Layer 2	Concrete	0.15	0.93	1800	960
	Layer 3	PVC foil	0.00015	0.19	1460	1100
	Layer 4	Stirodure	0.05	0.03	33	1260
	Layer 5	Cement screed	0.04	1.4	2100	1050
	Layer 6	Ceramic tiles	0.015	0.87	1700	920
Roof	Outside Layer	Roof tiles	0.03	0.99	1900	880
	Layer 2	Air gap/wood	0.035	0.14	550	2090
	Layer 3	Glass wool/wood	0.08	0.04	50	840
	Layer 4	Gypsum board	0.012	0.19	800	1090

. These building materials and constructions are usual in Serbian buildings and correspond to typical Serbian construction materials. The windows were double glazed with the air gap of 15 mm, and the U-value of 2.72 W/(m²K). Inward opening side-hung windows are implemented in modeled buildings. The ratio of the areas of glass surface to that of the external wall surface was 13.96%. Then, the total area of the exterior walls was 224 m² (with the roof of 358 m²) and that of the windows was 32 m².

The installed windows and doors on the building envelope provide the infiltration of 0.5 ach. The infiltration parameter has been adopted for load calculations to ensure minimum outdoor fresh air for building zones without any forced ventilation. It was assumed that these rooms would have almost the same occupancy, lighting, and small power schedule (see Figure 3).

The heating and cooling are assumed to operate according to the schedules, during the entire year, to meet the temperature heating and cooling setpoints given in

Table 2. Setpoint Schedule.

Heating			Cooling
Period	15 October to 15 April		Period	15 May to 15 September
06.00–22.00	20 °C	22 °C	06.00–22.00	24 °C
22.00–06.00	18 °C	18 °C	22.00–06.00	30 °C
Zone	Kitchen, living room, bedroom 1, bedroom 2	Toilet	Zone	Kitchen, living room, bedroom 1, bedroom 2

.

2.2. Location and Climate

The investigated residential buildings were located in the city of Belgrade (Republic of Serbia). Its average height above sea level is about 117 m, its latitude is 44°82′ N and longitude 20°28′ E. The time zone for Belgrade is GMT+1 h. Belgrade has a moderate continental climate with four defined seasons (winter, spring, summer, autumn). In the city of Belgrade summers are very warm and humid, while the winters are cool and snowy. The EnergyPlus uses weather data from its own database file, which contains a large variety of parameters: dry bulb temperatures (minimum and maximum), relative humidity, air pressure etc. Figure 4 represents monthly averages weather data for Belgrade—maximum and minimum air temperature and relative air humidity [28].

The EnergyPlus software also calculates solar radiation for every day in the year. Daily average solar radiation for Serbia is different in different parts of country: it is about 1.1 kWh/m² at the north and 1.7 kWh/m² at the south in January; in July it is about 5.9 kWh/m² at the north and 6.6 kWh/m² at the south of Serbia. Annually average solar radiation in Serbia is from 1200 kWh/m² for north-west to 1800 kWh/m² at the south of Serbia [29]. Solar radiation is dependent on the time of day and the sun’s angle toward Earth. This angle varies by latitude and longitude, and season. Also, atmospheric conditions can affect radiation levels—clouds, air pollution and the hole in the ozone layer. These factors cause typical radiation levels to differ. Figure 5 presents average monthly values of solar radiation (direct, diffuse and global) for Belgrade, obtained from EnergyPlus’ own weather file [29]. In accordance with the EnergyPlus software, direct solar radiation is measured as beam normal solar irradiance, while global and diffuse solar radiation are measured at a horizontal plane. That’s the reason why global solar radiation is not equal to the sum of direct and diffuse solar radiation.

2.3. Software–Simulation and Optimization

In this research, two software packages were used: EnergyPlus [28] and GenOpt [30]. With these packages, energy research was performed for three buildings: the basic building, the ORO building and the OBO building, shown in Figure 1. For the basic building, energy simulations were done by using EnergyPlus. By using the EnergyPlus and Genopt software, energy optimizations were performed for the ORO building and the OBO building.

The basic house shown in Figure 1a and the ORO house shown in Figure 1b were modeled by using idf files of EnergyPlus. Then, an idf model template which was made included four variables: the depth of south roof overhang (s_r), the depth of north roof overhang (n_r), the depth of west roof overhang (w_r), and the depth of roof east overhang (e_r). These variables are simultaneously varied between their minimum (0.2 m) and maximum values (3 m). For variation, the GPS HookeJeeves algorithm was used. The objective function (the minimum of E_tot) was programmed by Genopt code.

The OBO house shown in Figure 1c was modeled also by using an idf file of EnergyPlus, which included also four variables: the depth of south balcony overhang (s_b), the depth of north balcony overhang (n_b), the depth of west balcony overhang (w_b), and the depth of east balcony overhang (e_b). The objective function (the minimum of E_tot) was also programmed by using Genopt with HookeJeeves algorithm. At this idf model template, the values of (s_r), (n_r), (w_r), and (e_r) were put constant with the optimal values obtained for the ORO house. The simulation resultsare obtainedin the output file: theoptimumhorizontal roof overhangssize, power consumptionof heating, air conditioning, lighting and total primaryenergy consumption.

To simulate the energy performance of a building, the EnergyPlus software was used, in which the architecture and all system parameters that correspond to its physical condition are set. To ensure adequate thermal comfort in winter, electric heaters are used. This is not a typical heating system used in Serbian buildings. The most significant advantageous of using electric heaters are that they have the ability to fine-tune the temperature in the room and maintain a minimum temperature (as protection against freezing). In the space that is used periodically, it can be used for heating one room or the whole house.

Heating thermostats are set to the appropriate temperature during winter. In summer to maintain proper thermal comfort in rooms air conditioners are used with the appropriate thermostats. The room air conditioners are operated by electricity. To maintain an appropriate light level, the combined impact of daylight and electric lighting is investigated by entering the appropriate parameters in a given time interval (using the DayLightingControls function implemented in EnergyPlus) [28].

Finding the optimal size of the horizontal roof overhangs was done with the Hooke Jeeves optimization method [31] with the help of GenOpt [30]. The objective function minimizes the consumption of primary energy for heating, cooling and lighting of the building and energy spent to build a horizontal roof overhangs. The program GenOpt operates with fixed parameters, and with variable parameters in which the optimization is performed. Its Ini file defines the objective function and all necessary parameters and variables that are required for optimization. The command file is given as the pattern of the traits that are necessary for the execution of the optimization algorithm.

2.4. Energy Analyses of Modeled Buildings

In these investigations, energy analyses were performed with the aim to minimize primary energy consumption of modeled buildings with optimized size of overhangs. Also there were calculated some environmental performances of the buildings, like energy payback time and greenhouse substitution time.

2.4.1. Primary Operating Energy Consumption

The annual primary operating energy consumption of a house was calculated by equation:

E_p = (E_ac +E_eh +E_eq +E_el)K_ec/F,

(1)

Here, E_ac is annual electricity consumption by the air conditioners, E_eh is annual electricity consumption by the electric heaters, E_eq is annual electricity consumption for the electric equipment, E_el is annual electricity consumption for lighting, K_ec is primary energy factor and F is total conditioned floor area. The K_ec is defined as the ratio of the total primary energy consumption by energy sources and the total supplied electricity, and for Serbia K_ec = 3.04 [32].

2.4.2. Annualized Embodied Energy

The annualized embodied energy (AEE) for horizontal roof overhangsdepends on the overhang size (width, depth, and thickness) and material.

For the geometry of roof and its overhangs (see Figure 6), AEE_r (annualized embodied energy for ORO building) is calculated as

AEE_r (f_n F) = ρ_c δ_c s_ec A_c + ρ_ct δ_ct s_et (A_ct − A₀),

(2)

Here, ρ stands for the material density for roof overhangs (concrete, ρ_c = 2150 kg/m³ [1,2]; clay tile, ρ_ct = 1900 kg/m³ [1,2]), δ_c = 0.18 m stands for the thickness of the roof overhangs, δ_ct = 0.014 m stands for the thickness of the roof clay tile, s_e stands for the roof overhangs specific embodied energy (concrete, s_ec = 1.924 MJ/kg; clay tile, s_et = 6.5 MJ/kg) [33], and f_n stands for the roof overhangs lifecycle(20 years, [1,34]). Variable A_c stands for the area of the roof overhangs made by using concrete.

From Figure 6, this surface is obtained when the rectangle area (CNW CNE CSE CSW CNW) is subtracted from square area (BNW BNE BSW BSE BNW). Variable A₀ stands for the area of the tile roof surface without overhangs. This surface represents a sum of four roofs triangular surfaces of the same size A (“O CNW CNE O”, “O CNE, CSE O”, “O CSC, CSW O”, “O CSW, CNW O”). Variable A_ct stands for the areas of the tile roof surface with overhangs (optimization). This surface represents a sum of four roofs triangular surfaces A_n “O BNW BNE O”, A_e “O BNE, BSE O”, A_s “O BSC, BSW O”, A_w “O BSW, BNW O”.

When (A_ct − A₀) is multiplied by δ_ct, the volume of tiles is obtained because of increase in the roof area with established overhangs. The area of the roof overhangs made by using concrete (see Figure 6b) is given as:

A_c = L (e_r + w_r + n_r + s_r) + e_rn_r + e_rs_r + w_rs_r + w_rn_r,

(3)

In Figure 6b, e_r stands for the depth of roof overhang at the east building side, w_r stands for the depth of roof overhang at the west building side, n_r stands for the depth of roof overhang at the north building side and s_r stands for the depth of roof overhang at the south building side, L = 10.8 m stands for length of the buildings wall.

The difference between the areas of the tile roof surface with and without overhangs is given as:

(A_ct − A₀) = [(A_e,r − A) + (A_w,r − A) + (A_n,r − A) + (A_s,r − A)],

(4)

When the equations from (3) and (4) are substituted into (2), the following equation which describes the annualized embodied energy for ORO building is obtained:

AEE_r(f_nF) = {ρ_cδ_cs_sc[L(e_r + w_r + n_r + s_r) + e_rn_r + e_rs_r + w_rs_r + w_rn_r] + ρ_ctδ_cts_sct[(A_e,r − A) + (A_w,r − A) + (A_n,r − A) + (A_s,r − A)]},

(5)

The variable A (area) is calculated as:

A = Lh/2,  h = [(L/2)² + H²]^1/2,  A = L [(L/2)² + H²]^1/2/2,

(6)

Here, h_r = ((L/2)² + H²)^1/2 = 5.99 m = const., H = 2.6 m stands for the height of the roofand the values of x_e,r, x_w,rx_n,rx_s,r in A_i,r, A_w,r, A_n,r, and A_s,r are the following:

x_e,r = [(L/2 + e _r)² + H²]^1/2, x_w,r = [(L/2 + w_r)² + H²]^1/2
x_n,r = [(L/2 + n _r)² + H²]^1/2, x_s,r = [(L/2 + s_r)² + H²]^1/2,

(7)

Finally, the areas A_e,r, A_w,r, A_,r, and A_s,r are the following:

A_e,r = x_e,r (L+ s_r + n_r)/2 = (L + s_r+ n_r)[(L/2 + e_r)² + H²]^1/2/2
A_w,r = x_w,r (L + s_r + n_r)/2 =(L + s_r + n_r) [(L/2 + w_r)² + H²]^1/2/2
A_n,r = x_n,r (L + e_r + w_r)/2 =(L + e_r + w_r)[(L/2 + n_r)² + H²]^1/2/2
A_s,r = x_s,r (L + e_r + w_r)/2 =(L + e_r + w_r)[(L/2 + s_r)² + H²]^1/2/2,

(8)

When these values are substituted in (5) then:

AEE_r (f_nF) = {ρ_cδ_cs_sc[L (e_r + w_r + n_r + s_r) + e_rn_r + e_rs_r + w_rs_r + w_rn_r] + ρ_ctδ_cts_sct 1/2((L + s_r+n_r) [(L/2 + e_r)² + H²]^1/2 +(L + s_r + n_r) [(L/2 + w_r)² + H²]^1/2 +(L + e_r + w_r)[(L/2 + n_r)² + H²]^1/2 +(L + e_r + w_r) [(L/2 + s_r)² + H²]^1/2−4L [(L/2)² + H²]^1/2},

(9)

The annualized embodied energy (AEE_b) for horizontal balcony overhangs (Figure 6c) depends on overhang size (width, depth, and thickness) and material. AEE_b is calculated as:

AEE_b (f_b F) = ρ_c δ_b A_b s_ec,

(10)

where δ_b = 0.18 m stands for the thickness of the balcony overhangs, s_ec = 1.924 MJ/kg stands for the balcony overhangs embodied energy [8], f_b stands for the roof overhangs lifecycle (20 years). L = 10.8 m stands for the length of the buildings wall, h_b stands for the depth of the balcony overhangs.

The area of the roof overhangs made by using concrete (see Figure 6b) is given as:

A_b = L (e_b + w_b + n_b + s_b) + e_bn_b + e_bs_b + w_bs_b + w_bn_b,

(11)

In Figure 6c, e_b stands for the depth of balcony overhang at the east building side, w_b stands for the depth of balcony overhang at the west building side, n_b stands for the depth of balcony overhang at the north building side and s_b stands for the depth of balcony overhang at the south building side, L = 10.8 m stands for the length of the buildings wall.

2.4.3. Partial Annualized Primary Energy Consumption

The partial annualized primary energy consumption is equal to the sum of the primary operating energy consumption E_p and annualized embodied energy (AEE_r, AEE_b):

E_tot = E_p + AEE_r + AEE_b,

(12)

This equation is the objective function for the optimization routine. For the ORO building, the optimization is performed in respect to the four depths of the roof overhangs e, w, n, and s (when AEE_b = 0). For the OBO building, the optimization is performed in respect to the four depths of the balcony overhangs e_b, w_b, n_b, and s_b (when AEE_r = 0).

2.4.4. Primary Operating Energy Savings

When the optimized overhangs are installed, the achieved primary operating energy savings for heating, cooling and lighting in buildings (in percents) is given as:

e_psav = 100 (E_p,0 − E_p,opt)/E_p,0,

(13)

Here, E_p,opt stands for primary operating energy consumption after installation of optimized overhangs, E_p,0 stands for primary operating energy consumption without roof overhangs.

2.4.5. Energy Payback Time

Energy payback time (EPBT) is time, in years, required to primary energy savings disannul the primary energy spent to overhangs building, and it is given in next equation [35]:

EPBT = (AEE (f_n))/(E_p,0 − E_p,opt),

(14)

The energy recovery (ER) is defined as number of time cycles due to primary energy saving (generated during whole lifecycle) is more than the primary energy which is needed for overhangs building. The energy recovery (ER) is given by:

ER = (E_p,0 − E_p,opt)/AEE,

(15)

2.4.6. Greenhouse Substitution Time for Horizontal Overhangs

Greenhouse substitution time for horizontal overhangs (GHGST) is defined as the time period (in years) required for substituting the entire amount of CO₂ emitted during the construction of horizontal overhangs due to the effect of emission reductions from the operation of the same horizontal overhangs. The amount of CO₂ emitted in a process of production, transportation, building and installation of a horizontal roof overhangs (in t CO₂) [1,2] is:

G_CO2 = AEE_r(f_n) GHG_c,

(16)

where GHG_c stands for CO₂ emissions intensity of the production of concrete in tCO₂/t concrete. The annual decrease of the emission of CO₂ due to the application of horizontal roof overhangs is:

S_CO2 = (E_p,0 − E_p,opt) k_CO2,ec,

(17)

where k_CO2,ec stands for the equivalent to CO₂ emissions for an energy mix for electricity production. Then, CO₂ substitution time is given as:

GHGST = ρ δ l (h_E + h_S + h_W + h_N) GHG_c/[(E_p,0 − E_p,opt) k_CO2,ec],

(18)

3. Results and Discussion

Obtained optimal depths of the roof overhangs are listed in

Table 3. Results with implemented cooling, heating and lighting control.

	Depth of Overhangs (m)
	East	South	West	North
A0	0.2	0.2	0.2	0.2
A1	2.1	0.95	1.9	0.2
A2	2.6	0.7	2.4	0.4

. A0 represents the results for the basic building, A1 represent the results for the ORO building (with the optimized roof overhangs) and A2 represents the results for the OBO building (with optimized depths of balconies used as overhangs, the depths of roof overhangs are the same as that for the ORO building).

Basic building A0 has no overhangs, so the values of 0.2 m represent only roof protrusions on the second floor. For ORO building, with optimization routine it was obtained the maximum value of east roof overhang (2.1 m) and west roof overhang (1.9 m), while the south roof overhang was 0.95 m. For the OBO building (with optimal values for roof overhangs), a maximum value of the east balcony overhang of 2.6 m and a west balcony overhang of 2.4 m were obtained, while the south balcony overhang was 0.7 m and north balcony overhang was 0.4 m. These values can be explained by the small angle of incidence of the Sun in the morning and in the afternoon during the summer period, so solar gains during that period can be significant. With implementation of overhangs overheating can be avoided through the summer months, with a reduction of solar gains.

Values of solar radiation through the windows and its reduction, in the basic and OBO buildings (monthly) are presented in Figure 7. It is not difficult to conclude that solar gains through the windows at the OBO building are significantly lower than the solar gains through the windows of the basic building. Optimized horizontal overhangs provide great protection from the solar radiation (especially during the March–October period), preventing overheating and thus reducing cooling energy consumption, i.e., the total building energy consumption.

The total value of the annual solar radiation through the windows in the basic building is 13,404.7 kWh (57.29 kWh/m²), and in the OBO building with optimized overhangs it is 8451.11 kWh (36.12 kWh/m²). The annual difference in solar radiation of these two analyzed buildings is 4953.59 kWh (21.17 kWh/m²) and solar radiation is reduced by 36.95% (annually). The monthly reduction of solar radiation through the windows is lower in winter months, while it has a greater value during spring, summer and autumn months.

The specific final energy consumption for lighting, electric equipment, heating and air-conditioners for cooling (in kWh/m²) for all analyzed buildings is presented in Figure 8. With the implementation of overhangs, a small increase in annual lighting energy was observed for the ORO and OBO buildings compared to the basic building (0.23 kWh/m² and 0.53 kWh/m², respectively). Due to overhangs, a smaller amount of daylight enters these buildings, so electric lighting is used more during some time intervals (according to the software’s DayLightingControls function). In the winter period there are small solar gains through the windows of the ORO and OBO buildings, so the specific final heating energy consumption increases; for ORO building the increase of heating energy consumption is 2.63 kWh/m²; for OBO building the increase of heating energy consumption is 4.98 kWh/m². During the summer period, overhangs prevent building overheating, so the amount of cooling energy is significantly reduced. For the ORO building the decrease of annual cooling energy consumption is 6.18 kWh/m²; for the OBO building the decrease of annual cooling energy consumption is 11.9 kWh/m². The specific final energy consumption for electric equipment is the same for all the buildings, 21.98 kWh/m².

The total final and primary energy consumption for the analyzed buildings are shown in

Table 4. Final and primary energy consumption in analyzed buildings.

	Efinal	Eprim
A0	90.02	273.7
A1	86.70	263.6
A2	83.63	254.2

. The highest annual energy consumption corresponds to the basic building, case A0, (90.02 kWh/m² of final energy and 273.7 kWh/m² of primary energy), then the ORO building, case A1, (86.07 kWh/m² of final energy and 263.5 kWh/m² of primary energy), while the lowest energy consumption corresponds to the OBO building, case A2, (83.63 kWh/m² of final energy and 254.2 kWh/m² of primary energy). Annual energy savings are 3.69% for the ORO building, and 7.12% for the OBO building, compared to the basic building without horizontal overhangs.

The percentages of primary energy reduction and specific final energy reduction for the ORO and OBO buildings, compared to a basic house, are shown in Figure 9. Total primary energy consumption in the ORO building with the optimized roof overhangs (A1), was 3.69% lower, compared to the basic building without overhangs. Cooling energy consumption was 22.95% lower, while heating energy increased by 8.62%, in the form of energy consumption for lighting (2.1%). Significantly greater energy saving is achieved in OBO buildings with the optimized roof overhangs and optimized depths of balconies used as overhangs (A2)—total primary energy consumption in the OBO building is 7.12% lower, compared to the basic building. A greater cooling energy saving is also obtained (44.15%), while the primary heating energy was increased by 16.33%, mainly as energy consumption for lighting (4.98%). These values represent very significant energy savings.

The duration required for any primary energy savings to compensate for the primary energy needed to build overhangs, in accordance with Equation (14) is EPBT = 6.44 years for the ORO house, and EPBT = 6.60 years for the OBO house. The number of time primary energy savings (Equation (14)) are generated during the lifecycle by using the optimal overhangs more than the primary energy needed to build overhangs is ER= 3.11 for the ORO, and 3.03 for the OBO house (

Table 5. Embodied energy, AEEr, EPBT and ER.

	Embodied Energy			EPBT Years	ERTimes
	AEEr (kWh/m2)	AEErConcrete (kWh/m2)	AEErClay Tile (kWh/m2)
A0	/	/	/	/	/
A1	3.28	2.66	0.62	6.44	3.11
A2	6.44	5.82	0.62	6.60	3.03

).

The CO₂ substitution time (GHGST) is the time required to substitute the entire amount of CO₂ emitted during the construction of a technical system due to the effect of emission reductions resulting from operation of the system. The amount of CO₂ emitted during the construction of concrete horizontal roof overhangs is GCO₂ = 3.03 t CO₂. Then, the CO₂ emissions intensity of the concrete production is taken as GHGc = 0.13 t CO₂/t concrete from [35,36]. The CO₂ emission reductions resulting from the application of horizontal roof overhangs is annually S_CO2 = 2.07 t CO₂ where equivalent CO₂ emissions for EPS kCO_2,ec = 3.1, taken from [32]. Finally, the CO₂ substitution time is GHGST = 1.47 years.

Validation of the Results

The average annual specific primary energy consumption for the buildings which belong to the groups D1, E1 and F1, according to the national residential buildings typology in Serbia [26] (with applied thermal insulation, replaced old inefficient windows and no overhangs), is 281 kWh/m² [37]. This value is near the annual specific primary energy consumption for the basic building without overhangs, analyzed in these investigations (273.7 kWh/m²). The investigated basic building, like the ORO and OBO buildings, represents typical buildings from the D1, E1 and F1 groups, with thermal insulation on external walls and energy efficient windows. Having in mind these facts, it can be said that the data obtained by simulations and optimizations are valid.

4. Sensitivity to the Accuracy of the Input Data

In these investigations, optimization is performed for the horizontal roof overhangs. The overhangs are made by using concrete of the specific embedded energy (due its production process of materials, construction process, manufacture and installation) s_ec = 1.924 MJ/kg. As there are different conditions of concrete production and construction, specific embedded energy of concrete as input data may be different. An analysis, which presents how these changes influence to the output simulation results, for ORO and OBO building, is given below (

Table 6. Sensitivity to the accuracy of the specific embodied energy for ORO house.

ORO Building
	Depth of Horizontal Roof Overhangs				Energy
	EAST (hE)	SOUTH (hS)	WEST (hW)	NORTH (hN)	Eprim	Eac	Eeh	Eeq	Eel	ep%
	m	m	m	m	kWh/m2	kWh/m2	kWh/m2	kWh/m2	kWh/m2	%
Sec	0.2	0.2	0.2	0.2	273.7	26.95	30.51	21.98	10.58	/
Sec+20%	1.9	0.95	1.8	0.2	263.7	21.02	33.03	21.98	10.80	0.08
Secref	2.1	0.95	1.9	0.2	263.5	20.77	33.14	21.98	10.81	ref.
Sec-20%	2.1	0.95	2.2	0.51	262.8	20.50	33.24	21.98	10.81	−0.27

and

Table 7. Sensitivity to the accuracy of the specific embodied energy for OBO house.

OBO Building
	Depth of Horizontal Balcony Overhangs				Energy
	EAST (hE)	SOUTH (hS)	WEST (hW)	NORTH (hN)	Eprim	Eac	Eeh	Eeq	Eel	ep%
	m	m	m	m	kWh/m2	kWh/m2	kWh/m2	kWh/m2	kWh/m2	%
Sec	0.2	0.2	0.2	0.2	273.66	26.95	30.51	21.98	10.58	/
Sec+20%	2.2	0.7	2.1	0.2	254.64	15.43	35.32	21.98	11.04	0.16
Secref	2.6	0.7	2.4	0.4	254.24	15.05	35.49	21.98	11.11	ref.
Sec-20%	2.6	0.7	2.4	0.5	254.16	15.00	35.51	21.98	11.11	−0.03

):

e_p% = 100 (E_{prim +/−20%} − E_primref)/E_primref,

(19)

During optimization for ORO building, if the specific embodied energy s_ec increases by 20%, the depth of east and west roof overhangs decreases, increasing the primary energy consumption by 0.08%. In this case cooling energy increases, while heating energy decreases. If the specific embodied energy s_ec decreases by 20%, depth of west and north roof overhang increases, with a decreasing of the primary energy consumption by 0.27%. The amount of cooling energy decreases in this case, while heating energy increases.

During optimization for the OBO building, if the specific embodied energy s_ec increases by 20%, the depth of east, west and north roof overhangs decreases, increasing the primary energy consumption by 0.16%. In these simulations, cooling energy has a small increase, while heating energy has a small decrease. If the specific embodied energy s_ec decreases by 20%, depth of north roof overhang increases, decreasing the primary energy consumption by 0.03%. In this case, the amount of cooling energy has a small decrease, while amount of heating energy has a very small increase. The obtained results show a very small deviation (in the range of −0.03–0.16%) from the main results obtained by simulations and optimization process.

5. Conclusions

This paper represents a numerical investigation about how shading by horizontal roofs and balcony overhangs influences the annual primary and final energy consumption for heating, cooling and lighting in residential building in Serbia. Energy consumption is investigated for three buildings modeled in the EnergyPlus software in accordance with national residential buildings typology in Serbia. These buildings were detached with two-floors and they had almost the same characteristics. They only differed in their overhang characteristics such as type and dimensions. They were: (1) a basic building, (2) a building with optimized roof overhangs (ORO building), and (3) a building with optimized balcony overhangs (OBO building). The basic building had roof overhangs with depths of 0.2 m, the ORO building had optimized roof overhangs and the OBO building had optimized balcony overhangs (besides the roof overhangs with the depths as in the ORO building).

The optimal sizes of the horizontal overhangs, which are placed over the east, west, north, and south walls, are obtained by simultaneous operation of the two programs EnergyPlus and GenOpt. The aim of the optimization was to minimize the primary energy consumption for heating, cooling and lighting (embodied energy of concrete horizontal roof overhangs was taken into account).

Simulation results performed in this paper showed that horizontal overhangs on the analyzed buildings can reduce annual solar radiation through the windows by 36.95%. The reduction of the solar radiation through windows is less through the winter months than in summer months, so there is the possibility of optimizing the size of overhangs separately, for each side. This optimization process can achieve even greater energy savings and reduced primary energy consumption.

For the ORO building, the optimal dimensions of roof overhang depths are 2.1 m facing east, 0.95 m facing south, 1.9 m facing west and 0.2 m facing north. The reduction of heat gains due to solar radiation decreases the energy consumption for cooling by 22.95%, while the energy consumption for heating and lighting increases by 8.62 and 2.1%, respectively. Total primary energy consumption is reduced by 3.69%.

For the OBO building, the optimal dimensions of the depths of balconies used as overhangs, (the depths of roof overhangs are the same as that for the ORO house) are 2.6 m facing east, 0.7 m facing south, 2.4 m facing west and 0.4 m facing north. The reduction of heat gains due to solar radiation decreases the energy consumption for cooling by 44.15%, while the energy consumption for heating, and lighting are increased by 16.33% and 4.98%, respectively. The total primary energy consumption is reduced by 7.12%.

The time needed for the primary energy savings to compensate for the primary energy needed to build overhangs is 6.44 years for the ORO house and 6.60 years for the OBO house. The number of time cycles of primary energy savings generated during the lifecycle by using the optimal overhangs more than the primary energy needed to build overhangs is ER = 3.11 for the ORO and 3.03 for the OBO building. The CO₂ substitution time GHGST is 1.47 years.

In the sensitivity analyses, we investigated how changes of the specific embedded energy of concrete, as input data, influence to the output simulation results for the ORO and OBO buildings. The obtained results show a very small deviation from the main results obtained by simulations and optimization process (in the range of −0.03–0.16%). Energy Plus is a software package which is intensively validated and has been tested using the IEA HVAC BESTEST E100–E200 series of tests [25,32]. Regardless of the high accuracy of the obtained results, all software tools, no matter how good and powerful they may be, can give a certain deviation in terms of the accuracy of the results.

Implementation of the roof overhangs on the existing building involves nailing rafter extensions onto existing rafters. When the rafter extensions are installed, then sheathing and roofing is started. If the roof is near the end of its life cycle, it is a good time to reroof the entire house. In that case, the overhangs will be built together with the roof. The case of implementation of balcony overhangs on an existing building can be very difficult job. First, concrete pillars must be added at the building construction, after that connection elements between the building and pillars have to be installed, and finally the balconies can be built. This process is more complex than implementation of roof overhangs.

Our future research may deal with analyses of different types of roof (flat and sloped), different roof construction types used in Serbia and different kinds of shading elements. Then, the optimization results may be compared if the roof is built using concrete, steal, laminated wood, or classic wood. In addition, the economics should be analyzed to show how these solutions are acceptable in practice and what any eventual energy penalty of this acceptance is.