Minimizing the Standard Deviation of the Thermal Load in the Spent Nuclear Fuel Cask Loading Problem

Abstract

The paper assumes that, at the end of the operational period of a Spanish nuclear power plant, an Independent Spent Fuel Storage Installation will be used for long-term storage. Spent fuel assemblies are selected and transferred to casks for dry storage, with a series of imposed restrictions (e.g., limiting the thermal load). In this context, we present a variant of the problem of spent nuclear fuel cask loading in one stage (i.e., the fuel is completely transferred from the spent fuel pool to the casks at once), offering a multi-start metaheuristic of three phases. (1) A mixed integer linear programming (MILP-1) model is used to minimize the cost of the casks required. (2) A deterministic algorithm (A1) assigns the spent fuel assemblies to a specific region of a specific cask based on an MILP-1 solution. (3) Starting from the A1 solutions, a local search algorithm (A2) minimizes the standard deviation of the thermal load among casks. Instances with 1200 fuel assemblies (and six intervals for the decay heat) are optimally solved by MILP-1 plus A1 in less than one second. Additionally, A2 gets a Pearson’s coefficient of variation lower than 0.75% in less than 260s CPU (1000 iterations).

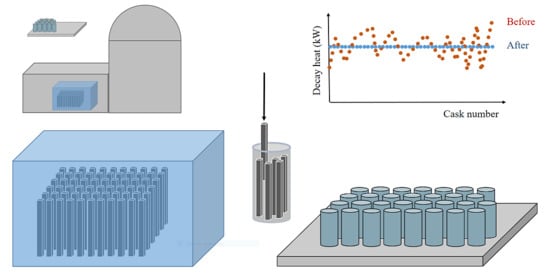
1. Introduction

Optimization problems are found at different levels in electric power systems, from both technological and operations management standpoints. In transport and distribution, not intending to make an exhaustive list, there are studies related to classical modeling and problem solving for electric energy distribution static planning [1,2,3]; other works, also on planning, propose a flexible distribution attending to the emerging variability of demand [4]. There are also many examples of optimization problems at the source point, from renewable generation (see for instance [5] for wind) to nuclear power.

A nuclear power plant is a complex system in which many optimization processes take place. The balance between safety requirements, competition in a liberalized electricity market, and access to limited human and material resources is resolved in nuclear power plants through an approach that prioritizes safety (see, for instance, INSAG-4 [6] and IAEA-TECDOC-1329 [7]).

Nuclear Power Plants (NPP) produce electricity from the heat released in a fission chain reaction; the so-called “nuclear fuel” is actually fissionable material. In Light Water Reactors (LWR), the type of reactor that constitutes the majority of the world’s nuclear fleet and the total of the Spanish fleet [8], nuclear fuel is made of uranium (slightly enriched in the ²³⁵U isotope), in the form of ceramic pellets of UO₂ protected and waterproofed by a metallic cladding (zirconium alloy) and grouped together, forming the so-called fuel assemblies (FA) [9]. The fuel used in the two units of Ascó NPP (the plant that has inspired the present study) is manufactured by ENUSA under a license agreement with Westinghouse, the owner of the technology [10].

Presently, the two Ascó units have fuel burn-up cycles of one and a half year. Each 18 months, some 60 FA (out of the 157 contained in the core of the reactor) are replaced (each one containing about 500 kg of uranium). Up to the end of its service, each Spent Fuel Assembly (SFA) has produced around 50 GWd/t of heat.

In the fission process, uranium atoms are transformed into radioactive fission products. Roughly speaking, in an SFA, some 5% of the initial uranium mass has undergone fission. A smaller part of the uranium is also transformed, through neutron capture nuclear reactions, into transuranic elements, which are also radioactive. The hazard of spent fuel is due to the potentially harmful effects of ionizing radiation. Thus, it is necessary to isolate the spent fuel for a long time to avoid the dispersion of the radioactive substances. An ultimate storage solution is proposed in repositories excavated in deep geological formations [11], in a way similar to that followed with chemical contaminants such as mercury [12].

The decay of radioactive substances in the spent fuel causes the so-called “decay heat”, which decreases as the activity of those substances declines, but which requires careful management of SFAs to prevent them from being damaged by excess temperature. After being removed from the core of the reactor, spent fuel is temporarily stored in the fuel pool of each power unit. Pool water provides shielding and cooling. Only when the power of the SFA has been sufficiently reduced can it be considered for dry storage in appropriate containers (either temporarily or permanently in a deep geological repository). The lack of political consensus for a definitive solution in Spain made it necessary to propose a Central Interim Storage Facility (CISF) [13], which was never built (now, it is proposed for 2028 [14]).

Over time, the spent fuel pools of the Spanish NPP have been reaching the limit of their capacity. In the case of the two units of Ascó, the pool in each of them can house 1421 FA, which is a figure that includes the 157 positions needed to discharge the entire reactor core if necessary. At the end of 2018, there were 1160 FAs in the Ascó 1 pool and 1104 in the Ascó 2 pool. The plant has 608 SFAs in an Independent Spent Fuel Storage Installation (ISFSI) in 19 HI-STORM containers [15], each hosting 32 SFAs [16].

In Spain, ENRESA (a state-owned company) is responsible for the decommissioning of the nuclear installations, as well as for the ultimate disposal of nuclear and radioactive wastes [17]. At the end of the exploitation period, it is in the interest of the plant operator to be able to transfer ownership of the installation to ENRESA in the shortest possible time. In order to do it, previously, all the fuel must be completely removed from the spent fuel pool [18]. At this moment, the ISFSI can be used as a logistics storage, housing spent fuel containers prior to transportation to the CISF. If the CISF is not yet available, the ISFSI should be usable as a full-scope storage (perhaps even in the long-term).

Thus, an optimization problem arises: it is necessary to remove all of the SFA from the pool within the minimum time and at the minimum cost [19]? Indeed, optimization problems can be found in a wide variety of operations in NPPs. For instance, in the spent fuel pool, where the SFAs are stored in racks, problems arise in optimizing the reliability of the design of the racks and the arrangement of the assemblies in the event of their possible displacement [20], and, as the capacity of the pool is limited to a specific number of assemblies, other management problems of spent nuclear fuel storage arise linked to this limitation [21]. At the right time, SFAs are removed from the pool and relocated in casks, often for long-term storage. The optimization here ranges from determining the SNF removal allocation strategy for a fleet of plants [22], to the design of the containers (e.g., what capacity, how much cooling time needed, etc.) [23], to the strategies to be followed in the loading of the casks.

As for the latter, Zerovnik et al. [24] propose combinatorial methods to optimize the cask loading, aiming at final geological repository. Considering as well the final deposition, Ranta and Cameron [25] used a two-phase heuristic method in order to minimize the thermal load of the canister with the largest load. Gomes et al. [26] propose a methodology, using genetic algorithms, to determine the optimal time to load the casks for dry interim storage, taking into account several cost factors. Spencer et al. [27] have develop a method (embedding greedy randomized adaptive search procedures in a memetic algorithm) to optimize the cask loading in a multi-objective search of configurations that minimize the number of casks, the thermal load, and the time when the transportation requirements are met.

In the present work, the cask loading problem is solved with two hierarchical optimization criteria: (i) minimize the cost of the regionalized casks necessary to relocate the spent fuel located in the pool at a given moment [28] using mixed integer linear programming [29]; and (ii) minimize the standard deviation of the thermal load in the set of casks using a multi-start metaheuristic with local search procedures [30].

In Section 2, we describe some dry storage systems for spent nuclear fuel. Section 3 is devoted to the description, modeling, and resolution of the spent nuclear fuel cask loading problem. Section 4 illustrates the procedure proposed in a case study inspired in Ascó NPP. Finally, Section 5 provides the conclusions derived from this work and a brief description of future research lines.

2. Dry Storage Systems for Spent Nuclear Fuel

Different solutions exist for the interim dry storage of spent nuclear fuel; as a comparison, the 14 closed sites in the USA use 11 different storage systems from four different suppliers [31].

In Spain, ENRESA has adopted different solutions. Some plants are using dual-purpose containers (transport and storage) whose structure provides shielding, confinement, and heat dissipation. Ascó’s two units are using the multi-purpose HI-STORM system, which is described below [15,16].

The spent fuel storage and transport system in Ascó is made up of different elements: the multi-purpose canister (MPC-32), the storage module (HI-STORM), the transport overpack (HI-STAR), and the transfer cask (HI-TRAC), which allows the MPC to be transferred to HI-STORM and HI-STAR [15] (see Figure 1).

The time required to completely remove the spent fuel from the pool depends on the minimum cooling time necessary for the last SFA to be loaded into a cask. This cooling period (that is, the time elapsed since the unload of the SFA from the reactor core) depends, in turn, on the type of container used and the technical specifications approved by the regulator for it.

To guarantee the integrity of the SFAs, the temperature of the metal cladding that surrounds the UO₂ pellets must be limited. This fact imposes requirements of sufficient heat dissipation in the cask design. However, also, it imposes a limit to the thermal power that the SFAs can generate inside the cask. For instance, in the HI-STORM system, under uniform charging conditions, each of the positions of the MPC-32 can house an SFA with a maximum power of 0.9375 kW at the time of loading (i.e., the total thermal power dissipated by the canister will be limited to 30 kW) [32]. The system allows regionalized loads; so, SFAs with higher decay heat can be located in the central region of the canister (region $R_a$, formed by 12 positions), at the cost of limiting the maximum power per position in the peripheral region (region $R_b$, 20 positions) and also limiting the total thermal load to a value less than 30 kW [33]. Figure 2 represents the positions assigned to each region.

In fact, the loading of a cask is constrained by the technical specifications in a more complex way, since they take into account, in addition to the cooling time, multiple fuel characteristics such as decay heat, burn-up, initial enrichment, the possibility that the assembly has some damage, or the possible presence of elements such as neutron sources, control rods, burnable poisons, etc. These conditions vary according to the type of cask, its use (storage or transport), and other specific limitations.

In what follows, it is assumed that at the end of the operational life of the plant, an ISFSI will exist that allows transfering all of the SFAs to it using the HI-STORM system (without imposing the present transport requirements, which are more restrictive than storage requirements). It is considered here that the storage requirements apply only to the decay heat of each SFA (calculated in turn from the burn-up, cooling time, and initial enrichment). The minimum time for the complete removal of all of the SFA from the pool is bounded by the moment when the hottest SFA fits into the requirements. The cost will depend on the number of containers to be used. So, the number of containers needed to remove all the SFA from the spent fuel pool needs to be minimized: this is the optimization problem addressed in the present study.

3. The Spent Nuclear Fuel Cask Loading Problem

In this section, we describe and formalize the spent nuclear fuel cask loading problem, and we propose a hybrid metaheuristic to solve it. Our method works in three phases using mixed integer linear programming (MILP), a deterministic algorithm, and local search heuristics.

3.1. Description of the Problem

At a given instant $T$, corresponding to the planned date for transferring in one go the contents of the spent fuel pool to the ISFSI, there are $n$ SFAs, forming a set $I$ $(i=1,\dots ,n$ ($n\equiv \left|I\right|$)).

At the time of removal, T, each fuel assembly $i\in I$ is characterized by a thermal power (decay heat), $q_i\left(T\right)$.

On the other end, there is an ISFSI ready to host all of the casks needed. Casks are regionalized, i.e., they are compartmentalized into regions with attributes of capacity and decay heat. Thus, there is a set of virtual regions $J$ ($j=0,1,\dots ,m$ ($\left|J\right|\equiv m+1))$, in which each type of region $\left(j\in J\right)$ is characterized by the upper and lower bounds on the decay heat a single SFA may have $\left[q_j^{-},q_j^{+}\right]$, and the number of SFAs in that region that can be held by a single cask, $h_j$. $j=0$ symbolizes the type of universal region capable of housing any fuel assembly without restrictions.

There is a set $K$ ($k=0,1,\dots ,l$ ($\left|K\right|\equiv l+1))$ of cask classes; $k=0$ symbolizes the universal class, which is capable of accommodating any fuel assembly without restrictions at an arbitrary high cost ${\gamma }_0\to \infty$. Each class is defined in relation to the maximum thermal load allowed in each region of the cask.

An adversity coefficient ${\gamma }_k$ is associated to each class of cask $\left(k\in K\right)$, corresponding to the arbitrary cost of selecting a cask of class $k\in K$ to house at least one SFA. We also assume for the class $k\in K$ a maximum number of units available, $d_k \left(\forall k\right)$. The total number of available casks is $D={{\displaystyle \sum }}_{\forall k}{d}_k$.

The relationship between a virtual region type $\left(j\in J\right)$ and a cask class $\left(k\in K\right)$ is given by matrix $B$, whose coefficients $b_{j,k} \left(\forall j\forall k\right)$ take the value 1 when the region of type $j\in J$ is associated to the cask of class $k\in K$, and 0 otherwise.

On the other hand, the relationship between the fuel assembly $i\in I$ and the type of region $j\in J$ is given by matrix $A\left(T\right)$, whose coefficients, $a_{i,j}\left(T\right) \left(\forall i\forall j\right)$, are equal to 1 when the fuel assembly $i\in I$ can be located in the region $j\in J$ at time $T$, and 0 in any other case; i.e., $a_{i,j}\left(T\right)=1\iff$ $q_i\left(T\right)\in \left[q_j^{-},q_j^{+}\right]$. It follows from it that the relationship between the fuel assembly $i\in I$ and the class of cask $k\in K$ is given by matrix $C\left(T\right)$ resulting from the boolean product of matrices $A\left(T\right)$ and $B$; that is, $C\left(T\right)=A\left(T\right)\otimes B$, thus fulfilling the following property: $(a_{i,j}\left(T\right)=1⋏b_{j,k}=1)\Rightarrow c_{i,k}\left(T\right)=1$.

Under such conditions [28], the spent nuclear fuel cask loading problem consists of transferring the maximum number of the fuel assemblies, which are located in the pool of a nuclear power plant on a date $T$ and expressed as time after the end of operation, into a set of regionalized casks of different classes, meeting the restrictions and minimizing costs (i.e., minimizing the total adversity).

3.2. Solving the Problem

As discussed above, our proposal solves the problem in three phases. The first phase uses MILP to allocate fuel assemblies to virtual regions with minimum cost (i.e., a minimum number of casks or minimum total adversity) [28]. In the second phase, a family of deterministic algorithms has been designed to assign each SFA to a specific cask actual region. Finally, in the third phase, a local search heuristic is proposed to minimize the standard deviation of the thermal load of the casks set.

3.2.1. Phase 1: MILP Model to Minimize the Cask Loading Cost

To formalize the proposed resolution methods, we use the following nomenclature.

Parameters:

$T$	Time or expected date to remove in one go the SFA from the pool in the nuclear power plant, expressed as time after the end of operation.
$I$	Set of SFA located in the pool of the nuclear power plant at time $T$. Let the elements be $i=1,\dots ,n$ ($n\equiv \left|I\right|$).
$J$	Set of virtual region types according to the upper and lower bounds on the decay heat of the SFAs. Let the regions be $j=0,1,\dots ,m$ with $\left|J\right|\equiv m+1$. The universal region, $j=0$, does not impose any limit; for practical purposes, the assigned elements to the universal region will remain in the pool.
$K$	Set of classes of casks: $k=0,1,\dots ,l$ with $\left|K\right|\equiv l+1$. The type of cask considered here corresponds to MPC-32 described above. We will assume that there is a type of universal container, $k=0$, associated with the universal region $j=0$; for practical purpose, the elements assigned to the universal container will remain in the pool.
$q_i\left(T\right)$	Decay heat of the fuel assembly $i\in I$ at the time $T$.
$q_j^{+}$	Upper limit of a single SFA’s decay heat in the virtual region $j\in J$.
$q_j^{-}$	Lower limit of a single SFA’s decay heat in the virtual region type $j\in J$. Here, we will assume $q_j^{-}=0 \forall j\in J$.
$A\left(T\right),a_{i,j}\left(T\right)$	Element–region compatibility matrix; technological coefficients $a_{i,j}$ equal to 1 if the fuel assembly $i\in I$ can be located in the virtual region $j\in J$ at time $T$, and 0 otherwise. Formally: $a_{i,j}\equiv a_{i,j}\left(T\right)=\left\{\begin{array}{cc}0,& if q_i\left(T\right)>q_j^{+}\\ 1,& \mathit{otherwise}\end{array}\right\}$.
$B,b_{j,k}$	Region-cask compatibility matrix; technological coefficients $b_{j,k}$ equal to 1 if the region of type $j\in J$ is associated with the cask class $k\in K$, and 0 otherwise.
$C\left(T\right),c_{i,k}\left(T\right)$	Element–cask compatibility matrix, which is defined as $C\left(T\right)=A\left(T\right)\otimes B$; technological coefficients $c_{i,k}\left(T\right)$ are equal to 1 when the element $i\in I$ can be placed in a cask of class $k\in K$ at time $T$, and 0 otherwise. Therefore, it is true that: $c_{i,k}\equiv c_{i,k}\left(T\right)=\left\{\begin{array}{cc}1,& if{{\displaystyle \sum }}_{\forall j\in J}{a}_{i,j}\left(T\right)\otimes b_{j,k}=1\\ 0,& \mathit{otherwise}\end{array}\right\}$.
$h_j$	Storage capacity of a region of type $j\in J$ measured by the number of SFAs a single cask can hold in that region at most.
$H_k$	Maximum storage capacity of a cask of class $k\in K$ measured by the number of fuel assemblies. The relationship $H_k={{\displaystyle \sum }}_{\forall j}{b}_{j,k}\times h_j$ is fulfilled.
$d_k,D$	Number of available casks of the class $k\in K$ at time $T$. The expected total cask availability is $D={{\displaystyle \sum }}_{\forall k}{d}_k$.
${\gamma }_k$	Adversity coefficient for a cask of class $k\in K$. The value ${\gamma }_k$ symbolizes the arbitrary cost if a cask of class $k\in K$ is selected to hold SFAs.

Variables:

$x_{i,j}$	Binary variable that equals 1 if the fuel assembly $i\in I$ is assigned to the virtual region $j\in J$, and 0 otherwise.
$y_j$	Number of fuel assemblies assigned to the virtual region $j\in J$.
$z_k$	Number of casks of class $k\in K$.
$\mathsf{\Gamma }\left(T\right)$	Total adversity function. It represents the overall cost of the casks used to hold the spent nuclear fuel on the scheduled date, $T$, after the pool of the nuclear power plant is emptied.

Using these parameters and variables, we formulate the following mathematical model.

MILP-1: Model for the assignment of fuel assemblies to types of virtual region

$$\mathit{min}\mathsf{\Gamma }\left(T\right)={\displaystyle \sum }_{k=0}^l{\gamma }_k{z}_k$$

(1)

Subject to:

$${\displaystyle \sum }_{i=1}^n{\displaystyle \sum }_{j=0}^m{x}_{i,j}=n$$

(2)

$${\displaystyle \sum }_{j=0}^m{a}_{i,j}{x}_{i,j}=1 \forall i=1,\dots ,n$$

(3)

$$y_j={\displaystyle \sum }_{i=1}^n{a}_{i,j}{x}_{i,j} \forall j=0,1,\dots ,m$$

(4)

$$z_k\ge \frac{b_{j,k}}{h_j}{y}_j\forall j=0,1,\dots ,m; \forall k=0,1,\dots ,l$$

(5)

$$z_k\le d_k \forall k=0,1,\dots ,l$$

(6)

$$x_{i,j}\in \left\{0,1\right\}\forall i=1,\dots ,n \forall j=0,1,\dots ,m$$

(7)

$$y_j\in {\mathbb{Z}}^{+}{{\displaystyle \cup }}^{\hspace{1em}}\left\{0\right\} \forall j=0,1,\dots ,m$$

(8)

$$z_k\in {\mathbb{Z}}^{+}{{\displaystyle \cup }}^{\hspace{1em}}\left\{0\right\} \forall k=0,1,\dots ,l$$

(9)

In the MILP-1 model, the objective Function (1) represents the minimization of the cask loading cost or total adversity, whose value coincides with the total number of casks when all the fuel assemblies are removed from the pool $\left(z_0=0\right)$ and the adversity coefficients are unitary for any class of cask $({\gamma }_k=1 \forall k=1,\dots ,l)$. Equalities (2) and (3) guarantee the assignment of all the fuel assemblies to any region, including the universal region $j=0$. Equality (4) determines the number of fuel assemblies that must be assigned to each type of region $j\in J$. Constraint (5) lower bounds the number of casks of each class $k\in K$, while Constraint (6) upper bounds that value according to their availability. Condition (7) imposes that the decision variables $(x_{i,j})$ are binary and, finally, the non-negativity and integrity of the auxiliary variables $y_j$ and $z_k$ are given by (8) and (9), respectively.

Running the MILP-1 model offers three types of results: (i) an optimal assignment of the fuel assemblies to the various virtual regions $(x_{i,j}^{*}\in \left\{0,1\right\}$ $\forall i\forall j)$, (ii) the optimal number of SFA assigned to each region $(y_j^{*}$ $\forall j)$, and (iii) the optimal number of casks of each class $(z_k^{*}$ $\forall k)$ corresponding to the minimum cost.

Although the previous results are interesting, the location of the fuel assemblies in the real regions of the casks remains to be determined.

3.2.2. Phase 2: Assignment of the Fuel Assemblies to the Real Cask Regions

Any sequence of objects corresponding to the triplet of sets $\left(I,J,K\right)$ can lead to a different solution. For example, if the sequence is built on the set $I$ of fuel assemblies, then the number of different ways to assign is $n!$ This can lead to an astronomical number of potentially different solutions for instances of realistic dimensions (e.g., $1164!$ in our case study). Based on this idea, we propose a family of constructive algorithms, $A1[\pi \left(n\right)$], which depends on the regulatory sequence $\pi \left(n\right)$ of the assignment of fuel assemblies to virtual regions.

Starting from an optimal solution given by MILP-1$(x_{i,j}^{*} \forall i\forall j, y_j^{*} \forall j, z_k^{*} \forall k)$, the procedure $A1\left[\pi \left(n\right)\right]$ creates a sequence $\pi \left(n\right)$ of fuel assemblies (Statement 5 in $A1\left[\pi \left(n\right)\right]$) to establish the sequence of assignment of SFAs to casks. Once the procedure determines the class of the cask $k_t^{*}$ that corresponds to the current element ${\pi }_t$, the element is recorded in the matrix $MPC32[·]$ (Statement 13 in $A1\left[\pi \left(n\right)\right]$), whose rows correspond to casks and whose columns correspond to positions within the cask. Subsequently, the heat loads $Q_{mpc32}[·]$in the casks are determined (Statement 16 in $A1\left[\pi \left(n\right)\right]$), and the elements are sequenced in the casks according to such loads (Statement 17 in $A1\left[\pi \left(n\right)\right]$). Finally, the results of the algorithm are returned (Statement 18 in $A1\left[\pi \left(n\right)\right]$).

Algorithm 1.$A1\left[\pi \left(n\right)\right]$: Algorithms to assign fuel assemblies to regions according to $\pi \left(n\right)$

// Initialization Input$I,\left(n,m,l\right),B\left[b_{j,k}\right],\left(q_i \forall i\right), (x_{i,j}^{*} \forall i\forall j), (y_j^{*}$$\forall j), (z_k^{*}$$\forall k),{\mathsf{{\rm P}}}^{\kappa }$ Initialize$t=0,MPC32\left[z_k^{*},32\right]=\{\varnothing \}$ // Create assignment sequence of SFAs $\pi \left(n\right)=\left({\pi }_1,{\pi }_2,\dots ,{\pi }_n\right)\leftarrow Generate\_sequence\left(I,n,{\mathsf{{\rm P}}}^{\kappa }\right)$ While ($t\le n)$ do Set$t=t+1$ // Find the virtual region assigned to element ${\mathsf{\pi }}_{\mathrm{t}}.$ Let $j_t^{*}$ Set$j_t^{*}=argma{x}_{\forall j}(x_{{\pi }_t,j}^{*})$ // Find cask class associated with region $j_t^{*}$. Let $k_t^{*}$ Set$k_t^{*}=argma{x}_{\forall k}\left(b_{j_t^{*},k}\right)$ // Record the SFA in the matrix MPC32 $MPC32[·]$$\leftarrow Record\_element\left(I,{\pi }_t,j_t^{*},k_t^{*}\right)$ End while // Calculate residual heat loads and order elements in matrix MPC32 $Q_{mpc32}[·]\leftarrow Calculate\_loads$($I,q_i,MPC32[·])$ $MPC32[·]\leftarrow Order\_elements\left(I,Q_{mpc32}[·],MPC32[·]\right)$ Return$Q_{mpc32}[·], MPC32[·]$ // End Algorithm $A1\left[\pi \left(n\right)\right]$

Note that Algorithm 1 $A1\left[\pi \left(n\right)\right]$ can generate many solutions thanks to the fact that the starting point is a permutation $\pi \left(n\right)$of the fuel assemblies of the set $I$ (Statement 5 in $A1\left[\pi \left(n\right)\right]$). Such permutations can be created using a family of rules ${\mathsf{{\rm P}}}^{\kappa }$ applied on the set $I$, which is initially ordered according to the SFA’s identifier ($i\in I$). The family of rules ${\mathsf{{\rm P}}}^{\kappa }$ can be of diverse nature; they may consist of the same initial sequence (lexicographic order) or the simple sequence of the elements according to the decay heat or in more complex rules used for the generation of neighborhoods (exchange and insertion) in algorithms based on trajectories through the search domain.

Obviously, all the solutions generated by $A1\left[\pi \left(n\right)\right]$ are optimal when the function objective is the minimization of the cost of the casks [28], as happens in Phases 1 and 2 of this work; however, when the objective function corresponds to another optimization criterion, such as the balancing of the heat load in the set of casks, $A1\left[\pi \left(n\right)\right]$ can be used in, at least, two ways:

(1)

In the construction phase (or phases) of multi-start algorithms, v.gr. greedy randomized adaptive search procedure (GRASP) algorithms, to build initial solutions to be used as seeds for the next phase of trajectory-based improvement in the search domain.

(2)

In the systematic generation of solutions, to assist metaheuristics based on populations (v.gr. genetic and memetic algorithms).

In this work, Algorithm 1 $A1\left[\pi \left(n\right)\right]$ constitutes one of the fundamental pillars for the construction of initial solutions, and the chosen way is (1).

3.2.3. Phase 3: Reduction of the Dispersion of the Thermal Load of the Casks

Phase 3 of the proposed procedure aims to reduce, by a predetermined number of iterations, the dispersion of the thermal load (measured in kW) in the set of casks. The dispersion metric to minimize chosen here is the standard deviation $\sigma \left(Q,T\right)$; this is:

$$\mathit{min}\sigma \left(Q,T\right)=\sqrt{\frac{1}{z_{tot}^{*}}{\displaystyle \sum }_{k=1}^l{\displaystyle \sum }_{{\delta }_k=1}^{z_k^{*}}{\left(Q_{{\delta }_k}-Q_{avg}\right)}^2}$$

(10)

where:

$z_{tot}^{*}$	Total optimal number of casks: $z_{tot}^{*}={{\displaystyle \sum }}_{\forall k}{z}_k^{*}$. It is obtained by applying the MILP-1 procedure by setting values to the adversity coefficient ${\gamma }_k$ $(\forall k\in K$).
$Q_{{\delta }_k}$	Total thermal load due to the SFA loaded on date $T$ in the ${\delta }_k$-th cask of class $k$: ${\delta }_k=1,\dots ,z_k^{*} \left(\forall k\in K\right)$. These values are obtained after applying the Algorithm 1 $A1\left[\pi \left(n\right)\right]$ by fixing a permutation $\pi \left(n\right)$ of the elements of set $I$.
$Q_{avg}$	Average value of the thermal load in the set of casks on date $T$: $Q_{avg}=\frac{{{\displaystyle \sum }}_{i\in I}{q}_i\left(T\right)}{z_{tot}^{*}}$
$\sigma \left(Q,T\right)$	Standard deviation of the thermal load in the set of casks on date $T$.

In order to carry out Phase 3, the non-exhaustive descent Algorithm 2 $A2\left[\pi \left(n\right)\right]$ is applied, based on local search optimization (see Algorithm 2 $A2\left[\pi \left(n\right)\right]$ below). Its main characteristics are as follows.

Phase 3.1: Initialization of Algorithm 2 $A2\left[\pi \left(n\right)\right]$

• An initial solution $X^0$ is obtained, applying the mathematical program MILP-1, after prefixing the values of the vector $\overrightarrow{\gamma }=({\gamma }_1,\dots ,{\gamma }_l$) of adversity coefficients; this solution is characterized by the triple of sets of values $(x_{ij}^{*} \forall i\forall j, y_j^{*} \forall j, z_k^{*} \forall k)$.
• The Algorithm 1 $A1\left[\pi \left(n\right)\right]$ is applied to the solution $X^0$, considering the arbitrary sequence $\pi \left(n\right)$, which initially corresponds to ${\pi }^0\left(n\right)$: the lexicographic order of the SFA’s identifiers ($i\in I$). Thus, the extended solution $X_{mpc}^0=\left\{X^0,\pi \left(n\right),MPC32\left[z_k^{*},32\right]\right\}$ is obtained, which contains detailed information on the location of each element inside the casks $z_k^{*} \left(\forall k\right)$ in the matrix $MPC32\left[z_k^{*},32\right]$.
• Solution $X_{mpc}^0$ is fixed as the incumbent solution of the local search iterative procedure $(X_{mpc}^{\mathrm{c}}\leftarrow X_{mpc}^0)$. In addition, $X_{mpc}^0$ is fixed as the best solution $(X_{mpc}^{*}\leftarrow X_{mpc}^0)$, and the standard deviation of this solution $\sigma \left(X_{mpc}^{*}\right)$ is determined.

Phase 3.2: Improvement of the initial solution with $A2\left[\pi \left(n\right)\right]$

• A tentative solution ${\widehat{X}}_{mpc}^{\mathrm{c}}$ belonging to the restricted neighborhood of the incumbent solution $X_{mpc}^{\mathrm{c}}$ is generated—that is, ${\widehat{X}}_{mpc}^{\mathrm{c}}\in \mathcal{N}\left(X_{mpc}^{\mathrm{c}},{\mathsf{{\rm P}}}^{LS},S_F\right)$—where ${{\rm P}}^{LS}$ is the rule for generating neighboring solutions and $S_F$ is the set of possible solutions. Specifically, given the incumbent solution $X_{mpc}^{\mathrm{c}}$, the generation rule ${{\rm P}}^{LS}$ operates as follows: for all pairs of different casks $({\delta }_k,{\delta }_{k^{\prime }})$ and all pairs of positions in these casks $\left(pos({\delta }_k\right),pos\left({\delta }_{k^{\prime }}\right))$, the tentative neighboring solutions $\left({\widehat{X}}_{mpc}^{\mathrm{c}}\right)$ exchange the elements between these positions, within the set of possible solutions $S_F$ that is regulated by the SFA–cask compatibility matrix $C\left(T\right)$.
• If the tentative solution ${\widehat{X}}_{mpc}^{\mathrm{c}}$ is a possible solution (${\widehat{X}}_{mpc}^{\mathrm{c}}\in S_F)$ and $\sigma \left({\widehat{X}}_{mpc}^{\mathrm{c}}\right)<\sigma \left(X_{mpc}^{*}\right)$, then the solution ${\widehat{X}}_{mpc}^{\mathrm{c}}$ becomes the best solution $\left(X_{mpc}^{*}\leftarrow {\widehat{X}}_{mpc}^{\mathrm{c}}\right)$ and also the new incumbent solution $\left(X_{mpc}^{\mathrm{c}}\leftarrow {\widehat{X}}_{mpc}^{\mathrm{c}}\right)$.
• The above steps are repeated within Phase 3.2 as long as there is an improvement to the incumbent solution or the number of tentative solutions generated does not reach the preset value ${\widehat{it}}^{\infty }$ (v.gr. ${\widehat{it}}^{\infty }=1000$ tentative solutions).

Algorithm 2.$A2\left[\pi \left(n\right)\right]$: Non-exhaustive local search descent algorithm based on $\pi \left(n\right)$

// Initialization Input$I,\left(n,m,l\right),C\left[c_{i,k}\right],\left(q_i \forall i\right), X^0,\pi \left(n\right),{\mathsf{{\rm P}}}^{LS},{\widehat{it}}^{\infty }$ $X_{mpc}^0\leftarrow Generate\_solution(X^0,A1\left[\pi \left(n\right)\right]$ $X_{mpc}^{\mathrm{c}}\leftarrow X_{mpc}^0; X_{mpc}^{*}\leftarrow X_{mpc}^0; iter=0$ // Solution improvement by local search Repeat ${\widehat{X}}_{mpc}^{\mathrm{c}}\leftarrow X_{mpc}^{\mathrm{c}}$; $exit=true; iter=iter+1$ $\mathcal{N}\left(X^c,{\mathsf{{\rm P}}}^{\kappa },S_F\right)\leftarrow Operator\_Neighbourhood\left(X_{mpc}^{\mathrm{c}},{\mathsf{{\rm P}}}^{LS},S_F\right)$ Repeat for all$X\in \mathcal{N}\left(X_{mpc}^{\mathrm{c}},{\mathsf{{\rm P}}}^{LS},S_F\right)$ If$\left[\sigma \left(X\right)<\sigma \left({\widehat{X}}_{mpc}^{\mathrm{c}}\right)\right]=true$then${\widehat{X}}_{mpc}^{\mathrm{c}}\leftarrow X$ Until ($\left[\sigma \left({\widehat{X}}_{mpc}^{\mathrm{c}}\right)<\sigma \left(X_{mpc}^{\mathrm{c}}\right)\right]=true)$ If$\left[\sigma \left({\widehat{X}}_{mpc}^{\mathrm{c}}\right)<\sigma \left(X_{mpc}^{\mathrm{c}}\right)\right]=true$then$X_{mpc}^{*}\leftarrow {\widehat{X}}_{mpc}^{\mathrm{c}}⋏X_{mpc}^{\mathrm{c}}\leftarrow {\widehat{X}}_{mpc}^{\mathrm{c}}⋏exit=false$ Until$\left(exit=true ⋎ iter\ge {\widehat{it}}^{\infty }\right)$ Return$\left\{X_{mpc}^{*}, \sigma \left(X_{mpc}^{*}\right)\right\}$ // End Algorithm $A2\left[\pi \left(n\right)\right]$

3.2.4. Multi-Start Metaheuristics Assisted by Assignment Sequences

The proposed metaheuristic integrates the procedures of the three phases described above (see Schema $MS\left[X^0,\pi \left(n\right)\right])$. This metaheuristic can be classified within the category of multi-start algorithms, since it uses a multitude of initial solutions generated by the algorithm $A1\left[\pi \left(n\right)\right]$ of Phase 2. In the generation of solutions, $A1\left[\pi \left(n\right)\right]$ uses a current sequence string $({\pi }^{\mathrm{c}}\left(n\right))$; this chain is progressively constructed by moderately altering the current sequence giving rise to the next ongoing permutation. The main characteristics of $MS[·]$ are the following:

• The Algorithm 3 metaheuristic $MS\left[X^0,\pi \left(n\right)\right])$ is initialized by executing Phase 3.1, starting with an initial solution $X^0$ offered by MILP-1 (Phase 1) and registering the sequence $\pi \left(n\right)$ as an assignment current sequence; that is: ${\pi }^{\mathrm{c}}\left(n\right)\leftarrow \pi \left(n\right)$.
• In a specific iteration, given an arbitrary current sequence, which we will denote as ${\pi }^{\mathrm{c}}\left(n\right)$, the algorithms $A1\left[\pi \left(n\right)\right]$ and $A2\left[\pi \left(n\right)\right]$ are cascaded, making ${\pi }^{\mathrm{c}}\left(n\right)\leftarrow \pi \left(n\right)$, and thus obtaining a solution $X_{mpc}^{*}\left({\pi }^{\mathrm{c}}\left(n\right)\right)$ that is locally optimal.
• In an iteration, to go from an ongoing assignment current sequence $({\pi }^{\mathrm{c}}\left(n\right))$ to the next current sequence $\left({\pi }^{ {\mathrm{c}}^{\prime }}\left(n\right)\right)$, there are many alternatives. Specifically, in this work, we have chosen to apply a slight mutation on the first sequence ${\pi }^{\mathrm{c}}\left(n\right)$. This mutation, characterized by the $P^m$ rule, consists of exchanging, in pairs, the fuel elements located in four positions of the current sequence chosen at random.
• Thus, for each $X^0$, the number of initial solutions locally optimized by $MS\left[X^0,\pi \left(n\right)\right]$ is equal to the number of sequences generated with the $P^m$ mutation rule. The $MS[·]$ procedure ends when the number of mutated sequences reaches a maximum value equal to $i{t}^{\pi \infty }$ (v.gr. $i{t}^{\pi \infty }=1000$ mutate sequences).

Algorithm 3.Metaheuristic$MS\left[X^0,\pi \left(n\right)\right]$: Three-Phase Hybrid Metaheuristics Based on $X^0$ and $\pi \left(n\right)$

// Initialization from a solution $X^0$ found by MILP-1 // (Phase 1) Input$X^0,\pi \left(n\right),{\mathsf{{\rm P}}}^{LS},{ \mathsf{{\rm P}}}^m,i{t}^{\pi \infty }$ ${\pi }^{\mathrm{c}}\left(n\right)\leftarrow \pi \left(n\right);iter=1$ $X_{mpc}^{\mathrm{c}}\leftarrow Generate\_solution\left(X^0,A1\left[\pi \left(n\right)\right]\right)$           // Initial solution from $A1\left[\pi \left(n\right)\right]$. $X_{mpc}^{*}\leftarrow Improve\_solution\left(X_{mpc}^{\mathrm{c}},A2\left[\pi \left(n\right)\right],{\mathsf{{\rm P}}}^{LS}\right)$ // Improved solution from $A2\left[\pi \left(n\right)\right]$. Repeat $\pi \left(n\right)\leftarrow Mutate\_sequence\left({\pi }^{\mathrm{c}}\left(n\right),{\mathsf{{\rm P}}}^m\right)$ ${\pi }^{\mathrm{c}}\left(n\right)\leftarrow \pi \left(n\right)$ $X_{mpc}^{\mathrm{c}}\leftarrow Generate\_solution\left(X^0,A1\left[{\pi }^{\mathrm{c}}\left(n\right)\right]\right)$        // Phase 2: Initial solution (iter). $X\leftarrow Improve\_solution\left(X_{mpc}^{\mathrm{c}},A2\left[{\pi }^{\mathrm{c}}\left(n\right)\right],{\mathsf{{\rm P}}}^{LS}\right)$   // Phase 3: Improved solution (iter). If$\left[\sigma \left(X\right)<\sigma \left(X_{mpc}^{*}\right)\right]=true$then$X_{mpc}^{*}\leftarrow X$ $iter=iter+1$ Until$\left(iter\ge i{t}^{\pi \infty }\right)$ Return$\left\{X_{mpc}^{*}, \sigma \left(X_{mpc}^{*}\right)\right\}$ // End Metaheuristic $MS\left[X^0,\pi \left(n\right)\right]$

4. Case Study

This section is dedicated to a case study inspired in the spent fuel pools of Ascó NPP (Tarragona, Spain). It contains the following points: (i) the model assumptions, (ii) the requirements for spent fuel cask loading, (iii) the procedures used, (iv) the data used, and (v) the results achieved.

4.1. Hypothesis for the Case

The following hypotheses are assumed for the case at hand:

Hypothesis 1 (H1). 

Fuel assemblies are characterized by their type, burn-up ($MWd/t$), initial enrichment (% by mass), and the time elapsed since they are unloaded from the core (in years). From these data, the decay heat of each element can be determined at the time it is transferred from the pool to the cask.

Hypothesis 2 (H2). 

There are no fuel assemblies damaged or affected by other additional constraints.

Hypothesis 3 (H3). 

The elements associated with the fuel, such as neutron sources, control rods, consumable poisons, and others, are not considered in the model.

Hypothesis 4 (H4). 

It is assumed that only one type of cask is available in terms of physical dimensions and number of positions for fuel assemblies, the MPC-32.

Hypothesis 5 (H5). 

The fuel assemblies are loaded into the casks taking into account the requirements for storage in module-type HI-STORM storage containers. It is assumed that there is no capacity limit in the ISFSI.

Hypothesis 6 (H6). 

The contents of the spent fuel pool at the end of the operation of the plant (T = 0) are assumed to be known. To carry out the case study, the real content of the spent fuel pool of NPP Ascó 1 is used here. The decay heat of each of the SFA at any given time T can be computed from their cooling time (this is T plus the time each SFA has previously spent in the pool) and the SFA’s burn-up and initial enrichment.

Hypothesis 7 (H7). 

The pool should be emptied using the minimum possible number of casks on the earliest possible date. The date has been chosen as T = 6 years in order to guarantee that even the hottest SFA meets the requirements.

Hypothesis 8 (H8). 

It may be interesting that the thermal load of the casks is balanced. Therefore, we aim at minimizing the standard deviation of the thermal load of the set of casks.

4.2. Requirements for the Storage of Fuel Assemblies

The requirements to take into account for emptying the pool are as follows:

R1.

Casks are of the MPC-32 type, which are compartmentalized in 32 positions, each one containing a single fuel assembly (see Figure 2).

R2.

The positions of a MPC-32 are grouped into two regions: ($R_a$) a permissive region with a high limit for the decay heat formed by $h_a=12$ positions and ($R_b$) a restrictive region with a low limit for the decay heat formed by $h_b=20$ positions.

R3.

A fuel encapsulation position (concept for which we will use the Latin noun locus–loci) can house an SFA whose cooling time is greater than 5 years (in our case, with T = 6 years, this does not constitute any limitation).

R4.

The contents of each locus in any cask must have a decay heat less than or equal to the maximum allowed in the locus: $q_a^{+}$ in region $R_a$ and $q_b^{+}$ in region $R_b$.

R5.

The maximum heat load allowed in a cask is equal to $Q_{MPC}^{+}=30 \mathrm{kW}$.

R6.

The maximum values for decay heat at loci are determined according to the case:

-

Case of uniform loading: the maximum decay heat allowed per locus in the MPC-32 equals $q_a^{+}=q_b^{+}=0.9375 \mathrm{kW}$ (30 $\mathrm{kW}/32$). Therefore, if all SFAs have a decay heat $q_i\left(T\right)\le 0.9375 \mathrm{kW} \forall i\in I$, then only one class of container is needed, and the problem has a trivial solution (in what concerns the minimization of the number of casks)

-

Case of regionalized loading: if any SFA has a decay heat $q_i\left(T\right)>0.9375 \mathrm{kW}$, then some casks allowing regionalized load are needed. In this case, the maximum values of decay heat per locus ($q_a^{+}$ or $q_b^{+}$) according to the region to which it belongs ($R_a$ o $R_b$) are determined as follows:

(1)

Set a value of the ratio of the maximum values of decay heat per locus $\rho =q_a^{+}/q_b^{+}$, such that$1\le \rho \le 3$ ($\rho =1$ corresponts to the uniform loading, $\rho =3$ is the maximum value allowed by the regulator for this ratio).

(2)

Determine the maximum allowed thermal load per locus,$q_b^{+}=q_b^{+}\left(\rho ,h_a,h_b\right)$ for the restrictive region $R_b$, from the expression:

$$(h_a\times \rho +h_b)\times q_b^{+}\left(\rho ,h_a,h_b\right)=f\left(\rho ,h_a,h_b\right)\times Q_{MPC}^{+}$$

(11)

where $f\left(\rho ,h_a,h_b\right)$ is a function bounded to 1 for $\rho =1$ and decreasing with $\rho$. The function $f\left(\rho ,h_a,h_b\right)$ for the MPC-32 is:

$$f\left(\rho ,h_a,h_b\right)=\frac{2}{\left(1+{\rho }^{\left(0.23/{\rho }^{0.1}\right)}\right)}.$$

(12)

(3)

Determine the maximum allowed thermal load per locus, $q_a^{+}\left(\rho ,h_a,h_b\right),$ for the permissive region $R_a$:

$$q_a^{+}\left(\rho ,h_a,h_b\right)=q_b^{+}\left(\rho ,h_a,h_b\right)\times \rho$$

(13)

4.3. Data and Other Characteristics of the Case

Obviously, the dimensions of the MILP-1 model are a function of the instances used. In this work, we use the ASCÓ#01_6.0 instance (see

Table A1. Set of SFAs corresponding to the Ascó instance #01_6.0. The characteristics are as follows: identifier $i \left(i=x+y\right)$ of the element, corresponding to row x and column y. The values in the table correspond to the decay heat $q_i\left(T\right)$ (in kW) for $T=6$ years.

x\y	1	2	3	4	5	6	7	8	9	10
0	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189
10	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189
20	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189
30	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189
40	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189	0.4189
50	0.4189	0.4189	0.4189	0.5979	0.5841	0.5789	0.5789	0.5962	0.5818	0.6080
60	0.5384	0.6084	0.5310	0.5766	0.5732	0.5784	0.6014	0.5801	0.5562	0.5721
70	0.5766	0.5477	0.5704	0.5477	0.5835	0.5302	0.5484	0.5318	0.5749	0.6098
80	0.6098	0.6098	0.5789	0.6010	0.5772	0.5236	0.5302	0.5302	0.5772	0.6049
90	0.5962	0.6101	0.5302	0.4772	0.4820	0.4756	0.4836	0.4740	0.4836	0.4756
100	0.4756	0.5335	0.6350	0.5979	0.6296	0.5962	0.6385	0.5997	0.5962	0.5979
110	0.5335	0.5997	0.5979	0.5962	0.6860	0.5351	0.5962	0.5940	0.6347	0.6010
120	0.6296	0.6332	0.6296	0.5927	0.5335	0.6917	0.6898	0.6165	0.6147	0.7068
130	0.4942	0.6183	0.6917	0.4925	0.6363	0.4942	0.4909	0.4958	0.4974	0.7105
140	0.4925	0.7442	0.6112	0.6898	0.4974	0.5875	0.5451	0.5853	0.5343	0.5401
150	0.5335	0.5451	0.5858	0.5444	0.5318	0.5418	0.5434	0.5910	0.5905	0.5841
160	0.5789	0.5302	0.5858	0.5335	0.5351	0.5327	0.5434	0.5418	0.5302	0.6955
170	0.7052	0.5055	0.5039	0.5813	0.5088	0.5270	0.5844	0.5064	0.5253	0.5031
180	0.5072	0.5270	0.6917	0.5831	0.6973	0.5023	0.5253	0.5848	0.5990	0.5467
190	0.5973	0.5533	0.5973	0.5500	0.6571	0.6571	0.5417	0.5417	0.6535	0.6094
200	0.5533	0.5973	0.6553	0.5939	0.5500	0.6025	0.5533	0.5550	0.6007	0.5384
210	0.6172	0.5351	0.6154	0.5360	0.6154	0.5394	0.5477	0.5236	0.6101	0.7112
220	0.5484	0.6119	0.5360	0.6154	0.5236	0.5494	0.5351	0.5477	0.5368	0.5410
230	0.5351	0.6137	0.6101	0.6442	0.6303	0.6512	0.6165	0.6355	0.6407	0.6233
240	0.6460	0.6442	0.6442	0.7673	0.6028	0.7593	0.6285	0.6079	0.6199	0.6407
250	0.5977	0.6233	0.6216	0.6407	0.7813	0.6199	0.6062	0.6477	0.6495	0.6079
260	0.6425	0.6390	0.6477	0.6045	0.6045	0.6407	0.6045	0.6285	0.6390	0.6320
270	0.6320	0.6355	0.6320	0.6355	0.6337	0.6372	0.6355	0.6407	0.6251	0.6372
280	0.6320	0.6337	0.6372	0.6442	0.6512	0.6460	0.7199	0.7180	0.6543	0.7238
290	0.6507	0.6490	0.6525	0.6525	0.6472	0.6490	0.6507	0.6454	0.6454	0.6578
300	0.6543	0.6525	0.7753	0.7793	0.7117	0.7117	0.7733	0.7713	0.7097	0.7203
310	0.7184	0.7165	0.7241	0.6923	0.7184	0.6923	0.6904	0.7260	0.7165	0.7203
320	0.7184	0.7203	0.6904	0.7184	0.7146	0.7071	0.7128	0.7071	0.7109	0.7090
330	0.7071	0.7109	0.7034	0.7222	0.7165	0.7146	0.7128	0.6757	0.6794	0.6775
340	0.6794	0.6757	0.6775	0.6775	0.6757	0.6218	0.4535	0.6261	0.6261	0.4566
350	0.6244	0.6279	0.4520	0.6289	0.6244	0.4489	0.6307	0.6783	0.6915	0.6839
360	0.6802	0.6972	0.6839	0.6991	0.6915	0.8315	0.8274	0.8336	0.8315	0.8212
370	0.8336	0.8233	0.8482	0.9784	0.9710	0.9759	0.9858	0.9735	0.9784	0.9759
380	0.9883	0.7239	0.7182	0.7258	0.7239	0.8357	0.8357	0.7599	0.7638	0.7677
390	0.8315	0.7658	0.7638	0.7638	0.7638	0.7284	0.7717	0.7638	0.7343	0.7323
400	0.8441	0.7304	0.7677	0.7677	0.7658	0.7658	0.7483	0.7386	0.7638	0.7463
410	0.7483	0.7483	0.7521	0.7502	0.7560	0.7463	0.7463	0.7502	0.7502	0.7463
420	0.7406	0.7776	0.7736	0.7795	0.7677	0.7680	0.7720	0.7620	0.7560	0.7640
430	0.7540	0.7640	0.7640	0.8666	0.8558	0.8623	0.8623	0.8558	0.8710	0.8688
440	0.8820	0.8952	0.8864	0.8886	0.8908	0.8842	0.8908	0.8886	0.9063	0.7704
450	0.7644	0.7724	0.7704	0.7882	0.7700	0.7720	0.7781	0.7744	0.7781	0.7680
460	0.7943	0.7923	0.7882	0.7842	0.7903	0.7842	0.7903	0.7882	0.7903	0.8579
470	0.7680	0.7720	0.8601	0.8514	0.7700	0.7761	0.8492	0.7903	0.7923	0.7943
480	0.7903	0.8128	0.7801	0.8086	0.8066	0.8046	0.8256	0.8128	0.8107	0.7882
490	0.8213	0.8046	0.7903	0.8149	0.8087	0.8192	0.7882	1.0027	0.9203	0.9955
500	0.9955	0.9249	1.0027	0.9180	0.9111	0.9180	0.9295	0.9931	0.9907	0.9835
510	0.9157	0.9157	0.9835	1.1306	1.1223	1.1278	1.1389	0.8030	0.8997	0.8907
520	0.8030	0.7968	0.9134	0.8974	0.8134	0.8303	0.8345	0.8367	0.8345	0.8303
530	0.8113	0.8134	0.8197	0.8093	0.8155	0.8218	0.8218	0.8303	0.8093	0.8155
540	0.8239	0.8261	0.8197	0.8134	0.8218	0.8439	0.8218	0.8527	0.8351	0.8197
550	0.8395	0.8197	0.8155	0.8218	0.8218	0.8483	0.8460	0.8373	0.8197	0.8218
560	0.8460	1.0201	0.7901	1.0176	1.0126	0.7989	1.0226	0.7814	0.7836	0.7923
570	0.7879	1.0126	1.0151	1.0076	0.7901	0.7749	1.0201	1.0076	1.0026	1.0026
580	1.0026	0.8483	0.8329	0.8329	0.8417	0.8395	0.8505	0.8329	0.8549	0.8615
590	0.8483	0.8527	0.8571	0.8460	0.8505	0.8571	0.8571	0.8929	0.8816	0.8839
600	0.8839	0.8285	0.8929	0.8861	0.8460	0.8351	0.8351	0.8839	0.8907	0.8771
610	0.8549	0.8727	0.8727	0.9916	0.8771	0.8549	0.8549	0.8615	0.9890	0.8749
620	0.8794	0.8704	0.9994	0.9890	0.8749	1.1196	1.1168	1.1306	1.1141	1.0868
630	1.0439	1.0814	1.0652	1.0519	1.0733	1.0281	1.0412	1.0439	1.0333	1.0733
640	1.0679	1.0652	1.0412	1.0254	1.0733	1.1196	1.1278	1.1168	1.1278	0.8965
650	0.8872	0.8895	0.8942	0.8895	0.8918	0.8965	0.8918	0.9036	0.8965	0.8918
660	1.0679	1.2543	1.0706	1.0679	1.2575	0.9106	1.2381	0.9083	1.0599	1.0760
670	0.9083	1.0706	1.0572	1.0652	0.8965	1.2543	0.9059	0.9036	0.9012	0.9059
680	0.9130	1.0603	0.9036	0.9177	0.9130	0.9059	0.9201	0.9012	0.8989	1.2510
690	1.2543	0.9012	1.2380	1.1614	1.2502	1.2336	1.1614	1.2367	1.1526	1.1496
700	1.1555	1.2428	1.2367	1.2306	1.2306	1.1585	1.1485	1.2367	0.9433	0.9408
710	0.9383	0.9408	0.9584	1.1233	1.1175	0.9534	0.9458	1.1146	1.1204	0.9508
720	0.9762	0.9609	0.9660	0.9762	1.0716	0.9788	0.9559	1.0859	1.0802	1.0830
730	0.9635	0.9813	1.0631	0.9839	1.0631	1.0575	0.9788	1.0547	0.9813	0.9762
740	0.9762	0.9813	1.0547	1.0660	1.0547	0.9890	0.9788	1.0603	0.9640	1.3368
750	1.3740	1.3638	1.3234	0.9775	1.3335	1.3436	1.3301	1.3503	1.3672	0.9721
760	1.3706	1.3436	1.3368	0.9667	1.0631	1.0547	1.0491	1.0575	1.0830	1.0688
770	1.0660	1.0745	1.0716	1.0745	1.0603	1.0716	1.0859	1.2543	1.2510	1.0773
780	1.0688	1.2575	1.2510	1.0745	1.0973	1.0887	1.0973	1.0944	1.2543	1.0916
790	1.0916	1.2608	1.2608	1.2608	1.0944	1.0887	0.8749	1.1093	0.8724	0.8698
800	1.1093	0.8826	1.1124	1.1185	1.1154	1.1185	0.8673	0.8749	0.8673	1.1124
810	1.1093	0.8749	1.1556	1.1494	1.1556	1.1587	0.5207	1.2124	1.2284	0.5186
820	0.5123	1.2252	1.2220	0.5207	1.2349	1.2510	1.2575	1.2317	1.0519	1.2349
830	1.2641	1.0609	1.0639	1.0639	1.2575	1.2349	1.2543	1.2092	1.2478	0.5375
840	1.2124	1.2478	1.2060	1.1997	1.2156	1.2029	1.2124	1.2446	1.2510	1.2060
850	1.2092	1.2381	0.5923	0.5947	0.5947	0.5923	0.4069	0.3913	0.5159	0.3975
860	0.4292	0.3975	0.3975	0.3975	0.4038	0.4785	0.4022	0.4651	0.3975	0.5133
870	0.5234	0.4372	0.4836	0.4325	0.5477	0.4635	0.5223	0.4524	0.5426	0.5375
880	0.4651	0.4603	0.5223	0.4571	0.4651	0.5156	0.5426	0.5273	0.5240	0.4492
890	0.4196	0.5206	0.4555	0.5223	0.4667	0.4603	0.4571	0.4135	0.5477	0.5140
900	0.5409	0.4196	0.5173	0.5460	0.5206	0.4619	0.5140	0.5190	0.4539	0.4587
910	0.4603	0.4089	0.5240	0.5140	0.4594	0.4820	0.4820	0.4787	0.4562	0.5455
920	0.4902	0.4934	0.5558	0.5507	0.4885	0.5167	0.4546	0.4771	0.4755	0.5576
930	0.5167	0.4117	0.4656	0.5015	0.4312	0.6366	0.6114	0.6120	0.4651	0.5190
940	0.4731	0.5257	0.4635	0.4476	0.5477	0.4683	0.5210	0.5012	0.4354	0.4700
950	0.5012	0.4656	0.4744	0.4554	0.4298	0.4554	0.4656	0.4729	0.4368	0.4714
960	0.5179	0.4312	0.5148	0.5179	0.4439	0.4397	0.4213	0.5256	0.4368	0.4326
970	0.4656	0.5148	0.4641	0.5133	0.5027	0.5012	0.4354	0.4583	0.4354	0.4598
980	0.5240	0.4368	0.4326	0.4997	0.5256	0.5287	0.5012	0.4997	0.5318	0.5302
990	0.5042	0.5019	0.5925	0.5033	0.4945	0.5957	0.4931	0.5019	0.4901	0.4887
1000	0.4960	0.5033	0.4901	0.5048	0.4989	0.6005	0.4960	0.6021	0.5989	0.4887
1010	0.5989	0.4975	0.5973	0.6053	0.5470	0.5078	0.5122	0.5063	0.5348	0.5424
1020	0.5394	0.4613	0.4628	0.4585	0.5394	0.4628	0.4599	0.5078	0.5152	0.5078
1030	0.5122	0.4599	0.4599	0.5409	0.4585	0.5152	0.5363	0.5048	0.5409	0.5237
1040	0.5713	0.5713	0.4706	0.4691	0.4576	0.5681	0.4547	0.4590	0.5713	0.4706
1050	0.4750	0.4735	0.4720	0.4532	0.4794	0.4750	0.5382	0.5305	0.4662	0.4504
1060	0.4518	0.4490	0.5382	0.4576	0.4633	0.4619	0.4619	0.4490	0.5539	0.4561
1070	0.4648	0.5602	0.5336	0.5351	0.4490	0.5554	0.5618	0.5336	0.4490	0.4677
1080	0.4518	0.5336	0.4561	0.5321	0.4604	0.5290	0.5290	0.4764	0.4750	0.5649
1090	0.5539	0.5398	0.5554	0.4604	0.4706	0.4720	0.4547	0.5602	0.4677	0.4461
1100	0.4677	0.4518	0.5336	0.4677	0.6512	0.6460	0.6407	0.6372	0.6407	0.6390
1110	0.6477	0.6390	0.6337	0.6530	0.6565	0.6601	0.6548	0.6495	0.6548	0.6601
1120	0.6905	0.6924	0.6924	0.6924	0.6690	0.6654	0.6672	0.6690	0.6708	0.6672
1130	0.6690	0.6708	0.7097	0.6407	0.7146	0.7184	0.7222	0.7146	0.7203	0.6794
1140	0.6739	0.6720	0.7146	0.6789	0.7203	0.7165	0.7165	0.6739	0.6720	0.7053
1150	0.7260	0.6684	0.7203	0.7184	0.6734	0.7146	0.7090	0.7260	0.7593	0.7494
1160	0.7475	0.7279	0.7534	0.7713

in Appendix A) as data for decay heat. The main characteristics of the experiment are as follows:

(1)

The number of spent fuel assemblies is equal to $n=1164$. The elements are identified with the indices $i\in I$ corresponding to the $n$ first natural numbers.

(2)

The expected date for the removal of elements from the pool is $T=6$ years after the end of operation. The decay heat values $q_i\left(T\right) \forall i\in I$ listed in Table A1 of Appendix A correspond to $T=6$ years.

(3)

The number of virtual regions of decay heat is equal to $m=6$. Let $r_j=\left\{q\in ℝ:q\in \left[q_j^{-}, q_j^{+}\right]\right\} \left(\forall j=0,1,\dots ,5\right)$ be those regions that are defined with closed intervals of decay heat per locus. The regions are specified from three values of the ratio of maximum thermal loads: $\rho =1,2,3$. Let:

$$r_0=\left\{q\in ℝ:q\in \left[0.00, 30 \mathrm{kW}\right]\right\}$$

$$r_1=\left\{q\in ℝ:q\in \left[0.00, 1.4250 \mathrm{kW}\right]\right\}$$

$$r_3=\left\{q\in ℝ:q\in \left[0.00, 0.9375 \mathrm{kW}\right]\right\}$$

$$r_4=\left\{q\in ℝ:q\in \left[0.00, 0.6310 \mathrm{kW}\right]\right\}$$

$$r_5=\left\{q\in ℝ:q\in \left[0.00, 0.4750 \mathrm{kW}\right]\right\}.$$

For convenience, virtual regions have been numbered in descending order of the upper limit $q_j^{+}$ $\forall j$ of each interval.

(1)

The definition of virtual regions ($r_0$ to $r_5$) allows establishing the element–region compatibility matrix $A\left(T\right)$, whose technological coefficients adopt the value 1 if the fuel assembly $i\in I$ can be assigned to a virtual region of type $j\in J$ at the time $T$, and 0 otherwise. Formally:

$$a_{i,j}\equiv a_{i,j}\left(T=6\right)=\left\{\begin{array}{cc}0,& if q_i\left(T=6\right)>q_j^{+}\\ 1,& \mathit{otherwise}\end{array}\right\} \forall i=1,\dots ,1164; \forall j=0,1,\dots ,5$$

(2)

The number of cask classes is $l=3$ if we omit the neutral virtual region r₀, which corresponds to the pool. The correspondence between the virtual regions ($r_1$ to $r_5$) and the real classes of the regionalized cask ($C{R}_1$ a C$R_3$) is established through the region-cask compatibility matrix $B$, whose coefficients $b_{j,k}$ are equal to 1 when the region $r_j$ $\left(j=1,\dots ,5\right)$ is associated with cask $C{R}_{\mathrm{k}}$ $\left(k=1,\dots ,3\right)$, and they are 0 otherwise. In our case, matrix $B$ is as follows:

$$B_{m\times l}=B_{5\times 3}=\left(\begin{array}{c}\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\\ \begin{array}{ccc} 0 & 1 & 0 \\ 1 & 0 & 0 \end{array}\end{array}\right)$$

Thus, a cask $C{R}_1$ is compartmentalized in a permissive region with the characteristics of $r_1$ and a restrictive region associated with $r_5;$ a cask $C{R}_2$ is associated with a permissive region $r_2$ and another restrictive $r_4$; and finally, a cask $C{R}_3$ has only one region with the qualities of the intermediate region r₃.

(1)

From a technological point of view, all the containers in this study correspond to MPC-32, with 12 positions in the permissive region and 20 positions in the restrictive regions. Obviously, an MPC-32 of class $C{R}_3$ has 32 positions in the unique region.

(2)

Taking into account that the number of cask classes is $l=3$, it remains to define the unit cost per each class. In order to measure the impact of the adversity coefficients ${\gamma }_k \left(\forall k\right)$ on the solutions offered by MILP-1, different values are given to the arbitrary costs $\overrightarrow{\gamma }=({\gamma }_1,{\gamma }_2,{\gamma }_3$).

(3)

Taking into account the values and characteristics exposed in the previous points, the dimensions of the MILP-1 model for the Ascó # 01_6.0 instance are the following: (i) 6984 binary decision variables $(x_{i,j})$ corresponding to the assignment of fuel assemblies to virtual regions; (ii) 6 integer variables $(y_j)$ associated with the number of fuel assemblies hosted by each virtual region; (iii) 4 representative integer variables ($z_k$) for the number of casks of each class; and (iv) 1195 constraints (1199 if the availability of casks is bounded).

4.4. Procedures

All compiled codes corresponding to the procedures used have been executed on a DELL Inspiron-13 (Intel(R) Core(TM) i7-7500U @ 2.70 GHz CPU 2.90 GHz, 16 GB de RAM, x64 Windows 10 Pro). The models and tools used to find the optimal solutions for this case study are the following:

(1)

Model MILP-1 [28] based on MILP that allows minimizing the cost $({\mathsf{\Gamma }}^{*}\left(T\right))$ of the containers required $(z_k^{*}$ $\forall k)$ to transfer all the SNF from the NPP pool. MILP-1 also offers the number of SFAs assigned to each region $(y_j^{*}$ $\forall j),$ as well as an optimal assignment $(x_{i,j}^{*} \forall i\forall j)$ of each SFA to a virtual region. For the exploitation of MILP-1, we use the IBM ILOG CPLEX solver (Optimization Studio v.12.2, win-x86-64).

(2)

Deterministic method $A1\left[\pi \left(n\right)\right]$ that starts from the result of MILP-1 and offers an assignment of SFAs to the permissive and restrictive regions of the casks based on the sequence of assignment of SFAs to casks $\pi \left(n\right)$. Here, 1000 consecutive allocation sequences are considered, which are generated by slightly mutating one of them to obtain the next, following the neighborhood transition rule $P^{LS}$. MILP-1 plus $A1\left[\pi \left(n\right)\right]$ (with lexicographic order of the fuel assembly codes) constitute the deterministic procedure $DP\left[\pi \left(n\right)\right]$ proposed in [28].

(3)

Local search heuristic $A2\left[\pi \left(n\right)\right]$ that starts from a solution generated by $A1\left[\pi \left(n\right)\right]$ and explores neighborhoods non-exhaustively until reaching a local optimum. The procedures MILP-1 plus $A1\left[\pi \left(n\right)\right]$ plus $A2\left[\pi \left(n\right)\right]$ (with the mutation rule $P^m$ applied to the $\pi \left(n\right)$ sequence in $i{t}^{\pi \infty }$ iterations) constitute the metaheuristic $MS\left[X^0,\pi \left(n\right)\right]$ proposed in this work.

In short, metaheuristic $MS\left[X^0,\pi \left(n\right)\right]$ works in this manner: from an optimal solution found by MILP-1, which is characterized by the triple of sets of values $[(x_{i,j}^{*} \forall i\forall j), (y_j^{*}$ $\forall j), (z_k^{*}$ $\forall k)]$, the algorithm $A1\left[\pi \left(n\right)\right]$ is applied $i{t}^{\pi \infty }$ times, transferring one by one and following $i{t}^{\pi \infty }$ sequences $\pi \left(n\right)$, the SFAs assigned to the virtual regions $r_j$ ($\forall j)$ toward the physical regions (permissive and restrictive) of the casks $C{R}_k$ $\left(\forall k\right)$, using the region-cask compatibility matrix $B$. Afterwards, the local optimization corresponding to heuristics $A2\left[\pi \left(n\right)\right]$ is applied to all $\left(i{t}^{\pi \infty }\right)$ solutions generated by algorithm $A1\left[\pi \left(n\right)\right]$.

4.5. Results

In addition to considering the solution from MILP-1 with the triplet ${\overrightarrow{\gamma }}_0=\left(1,1,1\right)$, which corresponds to minimizing the total number of casks, and in order to assess the impact of the adversity coefficients ${\gamma }_k \left(\forall k\right)$ on the solutions offered by MILP-1, 24 other optimal solutions are also analyzed, fixing the list of arbitrary costs $\overrightarrow{\gamma }=({\gamma }_1,{\gamma }_2,{\gamma }_3$) to the following values:

$${\overrightarrow{\gamma }}_1=\left(3,2,1\right), {\overrightarrow{\gamma }}_2=\left(3,1,2\right), {\overrightarrow{\gamma }}_3=\left(2,3,1\right),{\overrightarrow{\gamma }}_4=\left(2,1,3\right), {\overrightarrow{\gamma }}_5=\left(1,3,2\right),{\overrightarrow{\gamma }}_6=\left(1,2,3\right)$$

$${\overrightarrow{\gamma }}_7=\left(3,3,2\right),{\overrightarrow{\gamma }}_8=\left(3,3,1\right),{\overrightarrow{\gamma }}_9=\left(3,2,3\right),{\overrightarrow{\gamma }}_{10}=\left(3,2,2\right),{\overrightarrow{\gamma }}_{11}=\left(3,1,3\right),{\overrightarrow{\gamma }}_{12}=\left(3,1,1\right)$$

$${\overrightarrow{\gamma }}_{13}=\left(2,3,3\right),{\overrightarrow{\gamma }}_{14}=\left(2,3,2\right),{\overrightarrow{\gamma }}_{15}=\left(2,2,3\right),{\overrightarrow{\gamma }}_{16}=\left(2,2,1\right),{\overrightarrow{\gamma }}_{17}=\left(2,1,2\right),{\overrightarrow{\gamma }}_{18}=\left(2,1,1\right)$$

$${\overrightarrow{\gamma }}_{19}=\left(1,3,3\right),{\overrightarrow{\gamma }}_{20}=\left(1,3,1\right),{\overrightarrow{\gamma }}_{21}=\left(1,2,2\right),{\overrightarrow{\gamma }}_{22}=\left(1,2,1\right),{\overrightarrow{\gamma }}_{23}=\left(1,1,3\right),{\overrightarrow{\gamma }}_{24}=\left(1,1,2\right).$$

Using the deterministic procedure $DP\left[\pi \left(n\right)\right]$ proposed in [28], after obtaining an optimal solution with MILP-1 $[(x_{i,j}^{*} \forall i\forall j), (y_j^{*}$ $\forall j), (z_k^{*}$ $\forall k)]$, the algorithm $A1\left[\pi \left(n\right)\right]$ is applied following the sequence $\pi \left(n\right)$ corresponding to the lexicographic order of the fuel assembly identifiers. The global results of the 25 solutions are shown in

Table 1. Summary of results of the 25 optimal initial solutions (#0 to #24) provided by procedure $DP\left[\pi \left(n\right)\right]$ proposed in [28] for the Ascó #01_06 instance with the following technical characteristics: (i) 1164 Spent Fuel Assemblies (SFAs), (ii) T = 6 years, (iii) 6 virtual regions (including the neutral region) defined by three values of the ratio $\rho$ (1, 2, and 3), and (iv) 4 cask classes (including the neutral container).

Solution #	${\mathit{\gamma }}_1$	${\mathit{\gamma }}_2$	${\mathit{\gamma }}_3$	${\mathit{z}}_1^{*}$	${\mathit{z}}_2^{*}$	${\mathit{z}}_3^{*}$	${\mathit{z}}_{\mathit{t}\mathit{o}\mathit{t}}^{*}$	${\mathbf{\Gamma }}^{*} \left(\mathit{T}\right)$	${\mathit{Q}}_{\mathit{a}\mathit{v}\mathit{g}} \left[\mathbf{kW}\right]$	$\mathit{\sigma }\left(\mathit{Q}\right) \left[\mathbf{k}\mathbf{W}\right]$
#0	1	1	1	4	17	16	37	37	22.77	3.35
#1	3	2	1	2	17	18	37	58	22.77	3.29
#2	3	1	2	2	23	12	37	53	22.77	3.00
#3	2	3	1	19	0	24	43	62	19.59	4.42
#4	2	1	3	2	54	0	56	58	15.04	4.55
#5	1	3	2	19	0	24	43	67	19.59	4.61
#6	1	2	3	40	16	0	56	72	15.04	4.10
#7	3	3	2	6	13	18	37	93	22.77	3.20
#8	3	3	1	6	13	18	37	75	22.77	3.20
#9	3	2	3	2	23	12	37	88	22.77	2.90
#10	3	2	2	2	19	16	37	76	22.77	3.52
#11	3	1	3	2	54	0	56	60	15.04	4.49
#12	3	1	1	2	19	16	37	41	22.77	3.52
#13	2	3	3	9	13	15	37	102	22.77	3.11
#14	2	3	2	9	10	18	37	84	22.77	2.91
#15	2	2	3	4	21	12	37	86	22.77	3.37
#16	2	2	1	7	12	18	37	56	22.77	3.27
#17	2	1	2	2	23	12	37	51	22.77	2.93
#18	2	1	1	2	19	16	37	39	22.77	3.52
#19	1	3	3	83	0	0	83	83	10.15	2.97
#20	1	3	1	19	0	24	43	43	19.59	4.62
#21	1	2	2	9	13	15	37	65	22.77	3.13
#22	1	2	1	19	0	24	43	43	19.59	4.45
#23	1	1	3	33	23	0	56	56	15.04	4.30
#24	1	1	2	4	21	12	37	49	22.77	3.51

.

Specifically, in Table 1, the following data are collected for each solution (#0 to #24):

(1)

The cost $\overrightarrow{\gamma }=({\gamma }_1,{\gamma }_2,{\gamma }_3$) imputed to each cask class.

(2)

The optimal number of casks of each class $(z_k^{*}$ $\forall k)$ and the total number $(z_{tot}^{*}$) of casks required by each solution.

(3)

The optimal values of the objective cost function $({\mathsf{\Gamma }}^{*}\left(T\right)$ for the MILP-1 model.

(4)

The average thermal load corresponding to the configuration of each solution $(Q_{avg})$.

(5)

The standard deviation of the thermal load in the set of casks: $\sigma \left(Q\right)$.

Table 1 shows 16 optimal solutions that require 37 MPC-32, which is a number that also coincides with the minimum number of casks, according to the lower bound ($\lceil 1164/32\rceil$). However, these solutions show different values of the standard deviation of the thermal load, depending on the configuration of the 37 casks.

As an example, initial solution #9, one with the lowest thermal load dispersions between the casks: $\sigma \left(Q\right)=2.90$, corresponds to the triplet of costs ${\overrightarrow{\gamma }}_9=\left(3,2,3\right)$, in which it is considered that the adversity to the use of casks of classes $C{R}_1$ and $C{R}_3$ is 1.5 times higher that of class $C{R}_2$ casks.

Based on solution #9, the FAs column in Figure 3 shows the number of SFAs assigned to each virtual region, i.e., $y_1^{*}=24, y_2^{*}=274, y_3^{*}=369,y_4^{*}=457,y_5^{*}=40$. This is translated into a total requirement of 37 casks (see the MPC[z_k, h_j] column in Figure 3), $z_1^{*}=2, z_2^{*}=23$ and $z_3^{*}=12$ regionalized casks of classes $C{R}_1$, $C{R}_2$, and $C{R}_3$, respectively.

On the other hand, Figure 4 shows the detailed loads of the containers MPC-32 number n.1 (class $C{R}_1$), number n.3 (class $C{R}_2$) and number n.26 (class $C{R}_3$) of the initial solution #9. These loads are characterized by the identifiers and decay heat of the fuel assemblies located in each MPC-32.

In view of Figure 4, the following can be stated:

• Cask n.1 of initial solution #9 is class $C{R}_1$ with a permissive region $R_a\leftarrow r_1$ of 12 positions and a restrictive region $R_b\leftarrow r_5$ of 20. The 12 hottest assemblies in this cask are located in region $R_a$, so locus-1 is occupied by the fuel assembly 751 with a decay heat of 1.3740 kW, while the fuel assembly 753 (the last in $R_a$) is located in locus-12 with 1.3234 kW. Complementarily, 20 “cold” elements are located in positions 13 to 32 of the restrictive region $R_b$ of MPC-32 n.1, assembly 23 in locus-13, and assembly 21 in locus-32, whose decay heats are 0.4189 kW, coinciding with the decay heat of all the elements located in this region.
• Casks n.3 (initial solution #9) is class $C{R}_2$, with its permissive region $R_a\leftarrow r_2$ and its restrictive region $R_b\leftarrow r_4$. In region $R_a$, the 12 hottest elements of this cask are located with element 255 occupying locus-1 and element 281 located in locus-12 with residual heats equal to 0.7813 kW and 0.6320 kW, respectively. In addition, all the SFAs located in the restrictive region $R_b$ are considered to have a decay heat of 0.4189 kW.
• Finally, cask n.26 of initial solution #9 is class 3 with a uniform region consisting of 32 positions: $(R_a,R_b)\leftarrow r_3$. The loci-{1,12,13,32} are occupied by the elements 244, 126, 144, and 122, their respective decay heats being as follows: 0.7673, 0.6917, 0.6898, and 0.6332 kW.

Other interesting results shown in Figure 4 are as follows: (i) the total thermal load casks n.1, n.3, and n.26, which are 24.55, 16.39, and 21.59 kW, respectively; (ii) the thermal loads in the permissive and restrictive $(R_a,R_b)$ regions of these casks (v.gr. in MPC-32 n.26: 8.57 and 13.01 kW); (iii) the average thermal load, equal to 22.77 kW, corresponding to the load of the 1164 SFAs in the 37 casks that constitute initial solution #9; and, finally, (iv) the standard deviation of the thermal load associated with initial solution # 9, $\sigma \left(Q\right)=2.90 \mathrm{kW}$.

On the other end, to illustrate the performance of the $MS\left[X^0,\pi \left(n\right)\right]$ metaheuristic in terms of improving the standard deviation of the thermal load in the set of casks, nine solutions have been selected from the 25 solutions presented in Table 1. The solution selection criterion meets the following conditions:

(1)

Have a total number of $z_{tot}^{*}$ containers that is minimal; that is: $z_{tot}^{*}=37$.

(2)

If two or more solutions with $z_{tot}^{*}=37$, have the same configuration of containers by type $(z_1^{*},z_2^{*},z_3^{*})$, the one that presents smaller standard deviation $\sigma \left(Q\right)$ is chosen; for example, between solutions #2 and #9, we select solution #9.

The final solutions selected to apply Phase 3 to improve $\sigma \left(Q\right)$ using metaheuristic $MS\left[X^0,\pi \left(n\right)\right]$ are shown in

Table 2. Summary of results of the solutions selected to apply Phase 2 plus Phase 3 of the proposed procedure $MS\left[X^0,\pi \left(n\right)\right]$. The table shows the values: ${\sigma }_{A1}\left(Q\right)$, ${\sigma }_{A2}\left(Q\right)$, $i{t}^{*}$, $CP{U}_{i{t}^{*}}$, and $CP{U}_{100}$.

Solution #	${\mathit{z}}_1^{*}$	${\mathit{z}}_2^{*}$	${\mathit{z}}_3^{*}$	${\mathit{z}}_{\mathit{t}\mathit{o}\mathit{t}}^{*}$	${\mathbf{\Gamma }}^{*}\left(\mathit{T}\right)$	${\mathit{\sigma }}_{\mathit{A}1}\left(\mathit{Q}\right) \left[\mathbf{kW}\right]$	${\mathit{\sigma }}_{\mathit{A}2}\left(\mathit{Q}\right)$  $\left[\mathbf{k}\mathbf{W}\right]$	$\mathit{i}{\mathit{t}}^{*}$	$\mathit{C}\mathit{P}{\mathit{U}}_{\mathit{i}{\mathit{t}}^{*}}$ [s]	$\mathit{C}\mathit{P}{\mathit{U}}_{1000}$$\left[\mathbf{s}\right]$
#0	4	17	16	37	37	3.35	0.0001	998	652.3	654
#1	2	17	18	37	58	3.29	0.1059	127	97.5	608
#7	6	13	18	37	93	3.20	0.0008	107	80.7	583
#9	2	23	12	37	88	2.90	0.2240	73	56.2	635
#10	2	19	16	37	76	3.52	0.0001	535	422.8	729
#13	9	13	15	37	102	3.11	0.5464	647	421.7	605
#14	9	10	18	37	84	2.91	0.3364	10	7.9	511
#15	4	21	12	37	86	3.37	0.2772	662	487.5	717
#16	7	12	18	37	56	3.27	0.0008	83	62.8	643
Avg.	-	-	-	-	-	3.21	0.1658	360.2	254.4	632
Max	-	-	-	-	-	3.52	0.5464	998	652.3	729
Min	-	-	-	-	-	2.90	0.0001	10	7.9	511

. The indicators selected to compare these solutions are as follows: (i) the standard deviations ${\sigma }_{A1}\left(Q\right)$ and ${\sigma }_{A2}\left(Q\right)$ corresponding to the initial solutions provided by $A1\left[\pi \left(n\right)\right]$ and the improved solutions provided by $A2\left[\pi \left(n\right)\right]$, (ii) the iteration $i{t}^{*}$ corresponding to the best solution with $MS\left[X^0,\pi \left(n\right)\right]$; (iii) the computing time in seconds, $CP{U}_{i{t}^{*}}$, corresponding to the iteration $i{t}^{*}$; and (iv) the computing time in seconds, $CP{U}_{1000}$, given to $MS\left[X^0,\pi \left(n\right)\right]$ to improve 1000 initial solutions provided by $A1\left[\pi \left(n\right)\right]$ from a solution $X^0$ provided by MILP-1.

In view of Table 2, we can draw the following conclusions:

(1)

Metaheuristic $MS\left[X^0,\pi \left(n\right)\right]$ uses on average 632 s of CPU time to reach the best local optimum of 1000 initial solutions from algorithm $A1\left[\pi \left(n\right)\right]$. This average is included in the range of values [511, 729] in seconds.

(2)

Metaheuristic $MS\left[X^0,\pi \left(n\right)\right]$ takes on average 254.4 s of CPU time to obtain the best solution (locally optimized) from 1000 initial solutions generated by $A1\left[\pi \left(n\right)\right]$. This average is included in the range of values [7.9, 652.3] in seconds.

(3)

On average, the iteration $i{t}^{*}$ (best solution using $MS\left[X^0,\pi \left(n\right)\right]$) is $i{t}^{*}\approx 361$ (over 1000 iterations). This average is included in the range of values [10, 998] in iterations.

(4)

The procedure $DP\left[\pi \left(n\right)\right]$ proposed in [28] obtains, on average, solutions with a standard deviation of the thermal load equal to ${\sigma }_{A1}\left(Q\right)=3.21$. The range of values for ${\sigma }_{A1}\left(Q\right)$ is [2.90, 3.52].

(5)

On average, the metaheuristic $MS\left[X^0,\pi \left(n\right)\right]$ proposed in this work obtains solutions with a standard deviation of the thermal load of the set of casks equal to ${\sigma }_{A2}\left(Q\right)=0.1658$, from the solutions generated by $A1\left[\pi \left(n\right)\right]$ and the rule ${\mathsf{{\rm P}}}^{LS}.$ The range of values for ${\sigma }_{A2}\left(Q\right)$ is [0.0001, 0.5464].

(6)

On average, the standard deviation $\sigma \left(Q\right)$ is reduced approximately 20 times by applying the metaheuristic $MS\left[X^0,\pi \left(n\right)\right]$ versus procedure $DP\left[\pi \left(n\right)\right]$ proposed in [28].

To illustrate the reduction in the dispersion of the thermal load in the set of casks, Figure 5 shows the detailed loads of the containers MPC-32 number n.1 (type $C{R}_1$), number n.3 (type $C{R}_2$), and number n.22 (type $C{R}_3$) from solution #10 provided by metaheuristic $MS\left[X^0,\pi \left(n\right)\right]$.

Figure 6 and Figure 7 show graphically the thermal loads corresponding to the solutions provided by procedure $DP\left[\pi \left(n\right)\right]$ proposed in [28] (see Figure 6) versus metaheuristic $MS\left[X^0,\pi \left(n\right)\right]$ proposed in this work (see Figure 7) for each region (permissive and restrictive) and for each of the 37 casks. Note the significant differences that exist between the thermal loads of the 37 used MPC-32 in both figures, despite the fact that the containers present the same thermal limitation characteristics number by number (1 to 37).

In addition, Appendix B contains the detailed configurations of the 37 containers corresponding to solution #10 provided by metaheuristic $MS\left[X^0,\pi \left(n\right)\right]$.

5. Conclusions

A hybrid multi-start procedure assisted by mixed integer linear programming and local search optimization algorithms, that we have called here metaheuristic $MS\left[X^0,\pi \left(n\right)\right]$, has proven to be competitive in solving the spent fuel cask loading problem with minimal storage cost and a minimum standard deviation of thermal load. This is confirmed through the experiments carried out with the database of Ascó NPP. It allows generating instances with industrial dimensions (e.g., 1200 fuel assemblies and from 1 to 30 classes of regionalized casks, which translates into a number of decay heat virtual regions between 2 and 60).

The method proposed here, $MS\left[X^0,\pi \left(n\right)\right]$, to solve the single-stage cask loading of spent nuclear fuel is computationally competitive in its three phases: MILP-1 mathematical program, deterministic algorithm $A1\left[\pi \left(n\right)\right]$, and local search heuristic algorithm $A2\left[\pi \left(n\right)\right]$.

(i) The MILP-1 model is used to minimize the cost of casks required to host the nuclear fuel; it offers, as a solution, an optimal assignment of fuel assemblies to virtual thermal regions, in less than 0.5 CPU seconds, using instances with 1200 fuel assemblies, 6 types of regions, and 4 classes of casks. (ii) Algorithm $A1\left[\pi \left(n\right)\right]$, which starts from an MILP-1 solution, can assign the SFAs to the real regions of the casks in less than 0.25 s for the tested instances. (iii) The local search algorithm $A2\left[\pi \left(n\right)\right],$ based on 1000 initial solutions generated by $A1\left[\pi \left(n\right)\right]$ by slight mutations of the $\pi \left(n\right)$ sequences, is capable of reducing the initial values of the standard deviation $\sigma \left(Q\right)$ 20 times compared to the solutions provided by $\mathrm{procedure} DP[\pi \left(n\right)] \mathrm{proposed} \mathrm{in}$ [28], in an average CPU time equal to 4.24 min.

In other words, metaheuristic $MS\left[X^0,\pi \left(n\right)\right]$ (made up MILP-1 plus $A1\left[\pi \left(n\right)\right]$ plus $A2\left[\pi \left(n\right)\right]$) is capable of obtaining, on average, a solution with a Pearson’s coefficient of variation lower than 0.75% in less than 260s CPU (1000 iterations). In the slowest approximation, $MS\left[X^0,\pi \left(n\right)\right]$ obtains a solution with a Pearson’s coefficient of variation lower than 2.4%, starting from around 15.5% in little more than 12 min CPU (1000 iterations).

Future working lines taking advantage of these results include the following: (1) the formulation and exploitation of other models based on MILP for the regionalized cask loading according to several optimization criteria, and (2) the extension of the above models and procedures to the multi-stage load case.