Pore-Scale Lattice Boltzmann Simulation of Gas Diffusion–Adsorption Kinetics Considering Adsorption-Induced Diffusivity Change
Abstract
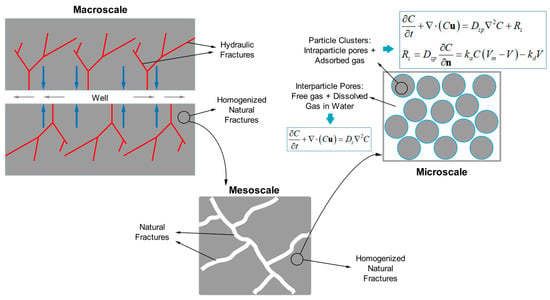
:1. Introduction
2. Lattice Boltzmann Method
2.1. The LB Equation for Fluid Flow
2.2. The LB Equation for Gas Diffusion–Reaction
2.3. Langmuir Adsorption Kinetic Equation
3. Physical Model and Verification
4. Results and Discussion
4.1. Diffusion –Adsorption of Gases in Simple Porous Media
4.2. Diffusion–Adsorption of Gas in 2D Reconstituted Porous Media
5. Conclusions
- (1)
- The influence of fluid velocity on the diffusion–adsorption process of coalbed methane at the pore-scale is very small and can be ignored; the magnitude of the FDC affects the spread range of gas diffusion and the process of adsorption and determines the position where adsorption takes place preferentially.
- (2)
- The magnitude of the adsorption constant controls the strength/rate of gas adsorption. A larger FDC or greater adsorption constant can effectively enhance the adsorption rate, and the trend of gas concentration- adsorption is closer to the Langmuir isotherm adsorption curve.
- (3)
- The gas diffusion–adsorption–desorption process is affected by the adsorption properties of coal. The specific performance is that the greater the pL or Vm, the slower the GDC decay. This is because the pL is related to the ability of gas–solid adsorption and desorption, the greater the pL means the faster the increment of the desorption rate than the adsorption rate, and the greater the Vm, the greater the adsorption capacity.
- (4)
- The effect of the gas molecular adsorption layer has a great impact on the kinetic process of gas diffusion–adsorption–desorption. For a coal matrix with a fixed space size, due to the limited gas adsorption amount, the results obtained by the kinetic diffusion–adsorption–desorption model will eventually return to the analytical solution of the static isotherm adsorption equation with sufficient time; however, coal is usually tight and has low permeability, so it is difficult to ensure that the gas diffusion and adsorption are sufficient, the direct use of static isotherm adsorption equation may be incorrect.
Author Contributions
Funding
Conflicts of Interest
Data Availability
References
- Rezaee, R. Fundamentals of Gas Shale Reservoirs; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Moore, T.A. Coalbed methane: A review. Int. J. Coal Geol. 2012, 101, 36–81. [Google Scholar] [CrossRef]
- Fathi, E.; Akkutlu, I.Y. Matrix Heterogeneity Effects on Gas Transport and Adsorption in Coalbed and Shale Gas Reservoirs. Transp. Porous Med. 2009, 80, 281. [Google Scholar] [CrossRef]
- Fu, X.; Qin, Y.; Wei, Z. Coalbed Methane Geology; China University of Mining and Technology Press: Xuzhou, China, 2007. [Google Scholar]
- Meng, Z.; Tian, Y.; Li, G. Theory and Method of Coalbed Methane Development Geology; Science Press: Beijing, China, 2010. [Google Scholar]
- Liu, K.; Ostadhassan, M.; Zhou, J.; Gentzis, T.; Rezaee, R. Nanoscale pore structure characterization of the Bakken shale in the USA. Fuel 2017, 209, 567–578. [Google Scholar] [CrossRef]
- Yuan, W.; Pan, Z.; Li, X.; Yang, Y.; Zhao, C.; Connell, L.D.; Li, S.; He, J. Experimental study and modelling of methane adsorption and diffusion in shale. Fuel 2014, 117, 509–519. [Google Scholar] [CrossRef]
- Feng, Y.-Y.; Yang, W.; Chu, W. Coalbed methane adsorption and desorption characteristics related to coal particle size. Chinese Phys. B 2016, 25, 068102. [Google Scholar] [CrossRef]
- Sing, K.S. Reporting physisorption data for gas/solid systems with special reference to the determination of surface area and porosity (Recommendations 1984). Pure Appl. Chem. 1985, 57, 603–619. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, Y.; Liu, S.; Chen, Z.; Yuan, L. Pore structure characterization of coal by synchrotron radiation nano-CT. Fuel 2018, 215, 102–110. [Google Scholar] [CrossRef]
- Zhang, D.; Kang, Q. Pore Scale Simulation of Solute Transport In Fractured Porous Media. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- Zhao, L.; Li, H. Stochastic Modeling of the Permeability of Randomly Generated Porous Media via the Lattice Boltzmann Method and Probabilistic Collocation Method. Transp. Porous. Med. 2019, 128, 613–631. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Z. Prediction of apparent permeability of porous media based on a modified lattice Boltzmann method. J. Pet. Sci. Eng. 2019, 174, 1261–1268. [Google Scholar] [CrossRef]
- Yu, B.; Li, J. Some Fractal Characters of Porous Media. Fractals 2001, 9, 8. [Google Scholar] [CrossRef]
- Ruckenstein, E.; Vaidyanathan, A.S.; Youngquist, G.R. Sorption by solids with bidisperse pore structures. Chem. Eng. Sci. 1971, 26, 1305–1318. [Google Scholar] [CrossRef]
- Karbownik, M.; Krawczyk, J.; Schlieter, T. The Unipore and Bidisperse Diffusion Models for Methane in Hard Coal Solid Structures Related to the Conditions in the Upper Silesian Coal Basin. Arch. Min. Sci. 2020, 65, 605–625. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, S.; Elsworth, D.; Jiang, Y.; Zhu, J. Pore Structure Characterization of Coal by Synchrotron Small-Angle X-ray Scattering and Transmission Electron Microscopy. Energy Fuels 2014, 28, 3704–3711. [Google Scholar] [CrossRef]
- Beaucage, G.; Kammler, H.K.; Pratsinis, S.E. Particle size distributions from small-angle scattering using global scattering functions. J. Appl. Cryst. J. Appl. Crystallogr. 2004, 37, 523–535. [Google Scholar] [CrossRef]
- Wang, K.; Wang, G.; Ren, T.; Cheng, Y. Methane and CO2 sorption hysteresis on coal: A critical review. Int. J. Coal Geol. 2014, 132, 60–80. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Bustin, R.M. The effect of pore structure and gas pressure upon the transport properties of coal: A laboratory and modeling study. 2. Adsorption rate modeling. Fuel 1999, 78, 1345–1362. [Google Scholar] [CrossRef]
- Do, D.D.; Wang, K. A new model for the description of adsorption kinetics in heterogeneous activated carbon. Carbon 1998, 36, 1539–1554. [Google Scholar] [CrossRef]
- Do, D.D.; Wang, K. Dual diffusion and finite mass exchange model for adsorption kinetics in activated carbon. AIChE J. 1998, 44, 68–82. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, W.; Dong, M.; Wang, J.; Li, Y.; Gong, H.; Sang, Q. A model of dynamic adsorption–diffusion for modeling gas transport and storage in shale. Fuel 2016, 173, 115–128. [Google Scholar] [CrossRef]
- Guo, Z.; Shu, C. Lattice Boltzmann Method and Its Applications in Engineering; Advances in Computational Fluid Dynamics; World Scientific: Singapore, 2013; Volume 3, ISBN 978-981-4508-29-2. [Google Scholar]
- He, Y.; Wang, Y.; Li, Q. Lattice Boltzmann Method: Theory and Applications; Science Press: Beijing, China, 2009. [Google Scholar]
- Kang, Q.; Wang, M.; Mukherjee, P.P.; Lichtner, P.C. Mesoscopic Modeling of Multiphysicochemical Transport Phenomena in Porous Media. Adv. Mech. Eng. 2010, 2, 142879. [Google Scholar] [CrossRef] [Green Version]
- Tian, Z.; Xing, H.; Tan, Y.; Gao, J. A coupled lattice Boltzmann model for simulating reactive transport in CO2 injection. Phys. A Stat. Mech. Its Appl. 2014, 403, 155–164. [Google Scholar] [CrossRef]
- Tian, Z.; Xing, H.; Tan, Y.; Gu, S.; Golding, S.D. Reactive transport LBM model for CO2 injection in fractured reservoirs. Comput. Geosci. 2016, 86, 15–22. [Google Scholar] [CrossRef] [Green Version]
- Kang, Q.; Lichtner, P.C.; Zhang, D. Lattice Boltzmann Pore-Scale Model For Multicomponent Reactive Transport In Porous Media. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Gan, Y.; Xu, A.; Zhang, G.; Succi, S. Discrete Boltzmann modeling of multiphase flows: Hydrodynamic and thermodynamic non-equilibrium effects. Soft Matter 2015, 11, 5336–5345. [Google Scholar] [CrossRef] [Green Version]
- Peng, Z.; Liu, S.; Li, Y.; Yao, Q. Apparent Permeability Prediction of Coal Matrix with Generalized Lattice Boltzmann Model considering Non-Darcy Effect. Geofluids 2020, 2020, 8830831. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann Method for Fluid Flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.; Cheng, Y.; Pan, Z.; Wang, K.; Liu, S. Gas diffusion in coal particles: A review of mathematical models and their applications. Fuel 2019, 252, 77–100. [Google Scholar] [CrossRef]
- Welty, J.; Wicks, C.E.; Rorrer, G.L.; Wilson, R.E. Fundamentals of Momentum, Heat and Mass Transfer, 6th ed.; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Xiong, X.; Devegowda, D.; Michel Villazon, G.G.; Sigal, R.F.; Civan, F. A Fully-Coupled Free and Adsorptive Phase Transport Model for Shale Gas Reservoirs Including Non-Darcy Flow Effects. In Proceedings of the SPE Annual Technical Conference and Exhibition; Society of Petroleum Engineers, San Antonio, TX, USA, 8–10 October 2012. [Google Scholar]
- Clarkson, C.R.; Bustin, R.M. Binary gas adsorption/desorption isotherms: Effect of moisture and coal composition upon carbon dioxide selectivity over methane. Int. J. Coal Geol. 2000, 42, 241–271. [Google Scholar] [CrossRef]
- Bustin, R.M.; Clarkson, C.R. Geological controls on coalbed methane reservoir capacity and gas content. Int. J. Coal Geol. 1998, 38, 3–26. [Google Scholar] [CrossRef]
- He, X.Y.; Li, N.; Goldstein, B. Lattice Boltzmann simulation of diffusion-convection systems with surface chemical reaction. Mol. Simulat. 2000, 25, 145–156. [Google Scholar] [CrossRef]
- Du, Z.; Zhang, X.; Huang, Q.; Zhang, S.; Wang, C. Investigation of coal pore and fracture distributions and their contributions to coal reservoir permeability in the Changzhi block, middle-southern Qinshui Basin, North China. Arab J. Geosci. 2019, 12, 505. [Google Scholar] [CrossRef]
- Montessori, A.; Prestininzi, P.; La Rocca, M.; Falcucci, G.; Succi, S.; Kaxiras, E. Effects of Knudsen diffusivity on the effective reactivity of nanoporous catalyst media. J. Comput. Sci. 2016, 17, 377–383. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Qu, Z.G.; Chen, L.; Tao, W.Q. Lattice Boltzmann simulation of gas–solid adsorption processes at pore scale level. J. Comput. Phys. 2015, 300, 800–813. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, K.; Liu, S.; Cheng, Y. Gas transport through coal particles: Matrix-flux controlled or fracture-flux controlled? J. Nat. Gas Sci. Eng. 2020, 76, 103216. [Google Scholar] [CrossRef]
- Su, X.; Lin, X.; Liu, S.; Zhao, M.; Song, Y. Geology of coalbed methane reservoirs in the Southeast Qinshui Basin of China. Int. J. Coal Geol. 2005, 62, 197–210. [Google Scholar] [CrossRef]
- Bohn, C.D.; Scott, S.A.; Dennis, J.S.; Müller, C.R. Validation of a lattice Boltzmann model for gas–solid reactions with experiments. J. Comput. Phys. 2012, 231, 5334–5350. [Google Scholar] [CrossRef]
- Peng, Z.; Liu, S.; Tang, S.; Zhao, Y.; Li, Y. Multicomponent Lattice Boltzmann Simulations of Gas Transport in a Coal Reservoir with Dynamic Adsorption. Geofluids 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, J.; Kabir, A.; Wang, J.; Pan, Z. Impact of Various Parameters on the Production of Coalbed Methane. SPE J. 2013, 18, 910–923. [Google Scholar] [CrossRef]











| Simulation area L × L (um × um) | 2 × 2 |
| Gas density ρg (kg/m3) | 0.7 |
| Gas viscosity (Pa·s) | 1.12 × 10−5 |
| Coal density ρc (kg/m3) | 1400 |
| Pressure gradient p (MPa/m) | 0.46 |
| Input concentration C0 (m3/t) | 1.6 × 10−2 |
| Gas diffusion coefficient in micro-fracture Ds (m2/s) | 7.84 × 10−5 |
| Langmuir volume Vm (m3/t) | 20 |
| Gas desorption constant kd (/s) | 2.94 × 106 |
| Langmuir pressure PL (MPa) | 2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Z.; Liu, S.; Li, Y.; Deng, Z.; Feng, H. Pore-Scale Lattice Boltzmann Simulation of Gas Diffusion–Adsorption Kinetics Considering Adsorption-Induced Diffusivity Change. Energies 2020, 13, 4927. https://doi.org/10.3390/en13184927
Peng Z, Liu S, Li Y, Deng Z, Feng H. Pore-Scale Lattice Boltzmann Simulation of Gas Diffusion–Adsorption Kinetics Considering Adsorption-Induced Diffusivity Change. Energies. 2020; 13(18):4927. https://doi.org/10.3390/en13184927
Chicago/Turabian StylePeng, Zhigao, Shenggui Liu, Yingjun Li, Zongwei Deng, and Haoxiong Feng. 2020. "Pore-Scale Lattice Boltzmann Simulation of Gas Diffusion–Adsorption Kinetics Considering Adsorption-Induced Diffusivity Change" Energies 13, no. 18: 4927. https://doi.org/10.3390/en13184927
APA StylePeng, Z., Liu, S., Li, Y., Deng, Z., & Feng, H. (2020). Pore-Scale Lattice Boltzmann Simulation of Gas Diffusion–Adsorption Kinetics Considering Adsorption-Induced Diffusivity Change. Energies, 13(18), 4927. https://doi.org/10.3390/en13184927