Comparative Analysis on Load Characteristic of Intermittently Conditioned Buildings for Different Wall Insulation Forms
Abstract
:1. Introduction
2. Method
2.1. Climate Conditions
2.2. Building Model
2.3. HVAC System
2.4. Internal Loads
2.5. Mathematical Formulation and Calculation Procedure
- (1)
- (2)
- (3)
- There exists thermal radiation between the room surfaces due to temperature difference. However, temperature difference will be reduced by adding insulation layer on the external walls, and hence some studies neglected this thermal radiation [4,15,22]. For simplicity, this thermal radiation is also ignored in the present study.
2.5.1. Heat Balance Equations of External Walls
2.5.2. Heat Balance Equations of Indoor Air
2.5.3. Heat Balance Equations of Internal Walls
2.6. Model Validation
3. Results and Discussion
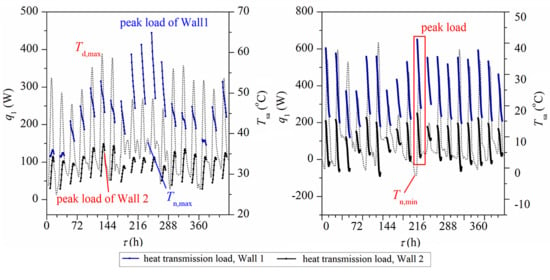
3.1. Effects of Insulation form on the Hourly Transmission Loads
3.2. Effects of Insulation form on Peak Loads
3.3. Effect of Insulation form on Daily Peak-Valley Load Difference
3.4. Effects of Insulation form on ACS Energy Consumption
3.5. Study Limitations
4. Conclusions
- (1)
- In the cooling season, when the wall insulated externally and internally, cooling transmission loads peaked in the day with the maximum mean outdoor temperature during the last ACS non-working period and with maximum mean sol-air temperature during ACS working time, respectively. Contrary to the cooling season, the heating transmission loads for the wall with external and internal insulation both peaked in the day with lowest mean outdoor temperature during the last ACS off period.
- (2)
- Compared with outside insulation, inside insulation gives lower peak loads. The peak cooling and heating loads of the room with interior insulation are at least 15% and 25% lower than that of the room with exterior insulation.
- (3)
- The steady running of ACS in winter is more difficult to realize in winter than in summer, meaning that decreasing peak-valley load difference of winter is more essential. When the insulation placed on the indoor surface, the peak-valley load difference is reduced greatly in winter. Thus, inside insulation can be considered a better way to maintain the ACS running steady.
- (4)
- A more significant energy saving can be achieved when insulation placed towards the inside, and this advantage of inside insulation is more significant in winter.
Author Contributions
Funding
Conflicts of Interest
References
- Wang, S.; Kang, Y.; Yang, Z.; Yu, J.; Zhong, K. Numerical study on dynamic thermal characteristics and optimum configuration of internal walls for intermittently heated rooms with different heating durations. Appl. Therm. Eng. 2019, 155, 437–448. [Google Scholar] [CrossRef]
- Zheng, X.; Lin, Z.; Xu, B.Y. Thermal conductivity and sorption performance of nano-silver powder/FAPO-34 composite fin. Appl. Therm. Eng. 2019, 160, 114–120. [Google Scholar] [CrossRef]
- Ozel, M.; Pihtili, K. Investigation of the most suitable location of insulation applying on building roof from maximum load levelling point of view. Build. Environ. 2007, 42, 2360–2368. [Google Scholar] [CrossRef]
- Al-Sanea, S.A.; Zedan, M.F. Improving thermal performance of building walls by optimizing insulation layer distribution and thickness for same thermal mass. Appl. Energy 2011, 88, 3113–3124. [Google Scholar] [CrossRef]
- Ozel, M. Effect of insulation location on dynamic heat-transfer characteristics of building external walls and optimization of insulation thickness. Energy Build. 2014, 72, 288–295. [Google Scholar] [CrossRef]
- Al-Sanea, S.A.; Zedan, M.F. Effect of insulation location on thermal performance of building walls under steady periodic conditions. Int. J. Ambient. Energy 2001, 22, 59–72. [Google Scholar] [CrossRef]
- Daouas, N. A study on optimum insulation thickness in walls and energy savings in Tunisian buildings based on analytical calculation of cooling and heating transmission loads. Appl. Energy 2011, 88, 156–164. [Google Scholar] [CrossRef]
- Kaynakli, A review of the economical and optimum thermal insulation thickness for building applications. Renew. Sustain. Energy Rev. 2015, 16, 415–425.
- Sadineni, S.B.; Madala, S.; Boehm, R.F. Passive building energy savings: A review of building envelope components. Renew. Sustain. Energy Rev. 2011, 15, 3617–3631. [Google Scholar] [CrossRef]
- Shekarchian, M.; Moghavvemi, M.; Rismanchi, B.; Mahlia, T.M.I.; Olofsson, T. The cost benefit analysis and potential emission reduction evaluation of applying wall insulation for buildings in Malaysia. Renew. Sustain. Energy Rev. 2012, 16, 4708–4718. [Google Scholar] [CrossRef]
- Barrios, G.; Huelsz, G.; Rojas, J. Thermal performance of envelope wall/roofs of intermittent air-conditioned rooms. Appl. Therm. Eng. 2012, 40, 1–7. [Google Scholar] [CrossRef]
- Tsilingiris, P.T. Wall heat loss from intermittently conditioned spaces—The dynamic influence of structural and operational parameters. Energy Build. 2006, 38, 1022–1031. [Google Scholar] [CrossRef]
- Zhang, R.; Nie, Y.; Lam, K.P.L.; Biegler, T. Dynamic optimization based integrated operation strategy design for passive cooling ventilation and active building air conditioning. Energy Build. 2014, 85, 126–135. [Google Scholar] [CrossRef]
- Yang, L.; Li, Y. Cooling load reduction by using thermal mass and night ventilation. Energy Build. 2008, 40, 2052–2058. [Google Scholar] [CrossRef]
- Yuan, L.; Kang, Y.; Wang, S.; Zhong, K. Effects of thermal insulation characteristics on energy consumption of buildings with intermittently operated air-conditioning systems under real time varying climate conditions. Energy Build. 2017, 155, 559–570. [Google Scholar] [CrossRef]
- China Academy of Building Research. The People’s Republic of China National Standard GB50189-2015, Design Standard for Energy Efficiency of Public Buildings (in Chinese); China Architecture and Building Press: Beijing, China, 2015. [Google Scholar]
- Yu, J.; Yang, C.; Tian, L.; Liao, D. A study on optimum insulation thicknesses of external walls in hot summer and cold winter zone of China. Appl. Energy 2009, 86, 2520–2529. [Google Scholar] [CrossRef]
- Raftery, P.; Lee, E.; Webster, T.; Hoyt, T.; Bauman, F. Effects of furniture and contents on peak cooling load. Energy Build. 2014, 85, 445–457. [Google Scholar] [CrossRef] [Green Version]
- Friess, W.A.; Rakhshan, K.; Hendawi, T.A.; Tajerzadeh, S. Wall insulation measures for residential villas in Dubai: A case study in energy efficiency. Energy Build. 2012, 44, 26–32. [Google Scholar] [CrossRef]
- Al-Sanea, S.A. Thermal performance of building roof elements. Build. Environ. 2002, 37, 665–675. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, K.; Zhang, Q.; Di, H. Ideal thermophysical properties for free-cooling (or heating) buildings with constant thermal physical property material. Energy Build. 2006, 38, 1164–1170. [Google Scholar] [CrossRef]
- Yam, J.; Li, Y.; Zheng, Z. Nonlinear coupling between thermal mass and natural ventilation in buildings. Int. J. Heat Mass Transf. 2003, 46, 1251–1264. [Google Scholar] [CrossRef]
- China Academy of Building Research. Code for Thermal Design of Civil Building GB 50176-2016, Ministry of Housing and Urban-Rural Development of the People’s Republic of China (in Chinese); China Architecture and Building Press: Beijing, China, 2016. [Google Scholar]
- Royapoor, M.; Roskilly, T. Building model calibration using energy and environmental data. Energy Build. 2015, 94, 109–120. [Google Scholar] [CrossRef] [Green Version]














© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, L.; Wang, Z.; Huang, Y.; Wang, X. Comparative Analysis on Load Characteristic of Intermittently Conditioned Buildings for Different Wall Insulation Forms. Energies 2020, 13, 4974. https://doi.org/10.3390/en13184974
Yuan L, Wang Z, Huang Y, Wang X. Comparative Analysis on Load Characteristic of Intermittently Conditioned Buildings for Different Wall Insulation Forms. Energies. 2020; 13(18):4974. https://doi.org/10.3390/en13184974
Chicago/Turabian StyleYuan, Liting, Zhiyi Wang, Yanyan Huang, and Xiaolong Wang. 2020. "Comparative Analysis on Load Characteristic of Intermittently Conditioned Buildings for Different Wall Insulation Forms" Energies 13, no. 18: 4974. https://doi.org/10.3390/en13184974
APA StyleYuan, L., Wang, Z., Huang, Y., & Wang, X. (2020). Comparative Analysis on Load Characteristic of Intermittently Conditioned Buildings for Different Wall Insulation Forms. Energies, 13(18), 4974. https://doi.org/10.3390/en13184974