Dynamic Response of an Inverted Pendulum System in Water under Parametric Excitations for Energy Harvesting: A Conceptual Approach
Abstract
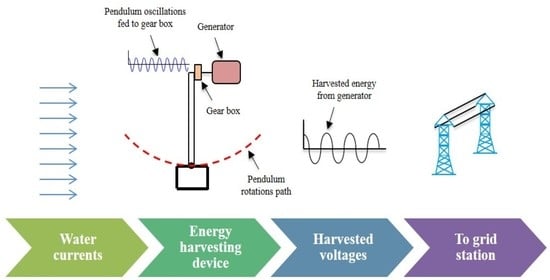
:1. Introduction
2. Statement of Problem Formulation
2.1. Pendulum System in Vacuum
2.2. Pendulum System in Water
3. Parametric Excitation Control
3.1. Parametric Excitation Control of an Inverted Pendulum in Vacuum
3.2. Parametric Excitation Control of Inverted Pendulum in Water
4. Numerical Simulation Results
Maximum Energy Harvesting
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shah, U.H.; Hong, K.-S. Input shaping control of a nuclear power plant’s fuel transport system. Nonlinear Dyn. 2014, 77, 1737–1748. [Google Scholar] [CrossRef]
- Martins, D.; Silveira-Neto, A.; Steffen, V., Jr. A Pendulim-based model for fluid structure interaction analysis. Rev. Eng. Térmica 2007, 6, 76–83. [Google Scholar] [CrossRef]
- Chatjigeorgiou, I. On the parametric excitation of vertical elastic slender structures and the effect of damping in marine applications. Appl. Ocean Res. 2004, 26, 23–33. [Google Scholar] [CrossRef]
- Lee, G.H.; Lee, H.J.; Choi, H.J.; Jeon, H.J.; Jung, S. Application of mobile inverted pendulum systems to Boxingbots for a boxing game. In Proceedings of the 2009 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Singapore, 14–17 July 2009; pp. 963–968. [Google Scholar]
- Lenci, S.; Brocchini, M.; Lorenzoni, C. Experimental rotations of a pendulum on water waves. J. Comput. Nonlin. Dyn. 2012, 7, 011007. [Google Scholar] [CrossRef]
- Kopman, V.; Laut, J.; Acquaviva, F.; Rizzo, A.; Porfiri, M. Dynamic modeling of a robotic fish propelled by a compliant tail. IEEE J. Ocean Eng. 2014, 40, 209–221. [Google Scholar] [CrossRef]
- Pathak, K.; Franch, J.; Agrawal, S.K. Velocity and position control of a wheeled inverted pendulum by partial feedback linearization. IEEE Trans. Robot. 2005, 21, 505–513. [Google Scholar] [CrossRef]
- Gordillo, F.; Aracil, J. A new controller for the inverted pendulum on a cart. Int. J. Robust Nonlin. 2008, 18, 1607–1621. [Google Scholar] [CrossRef] [Green Version]
- Spong, M.W. The swing up control problem for the acrobot. IEEE Control Syst. Mag. 1995, 15, 49–55. [Google Scholar]
- Spong, M.W.; Corke, P.; Lozano, R. Nonlinear control of the reaction wheel pendulum. Automatica 2001, 37, 1845–1851. [Google Scholar] [CrossRef]
- Jung, S.; Cho, H.-T.; Hsia, T.C. Neural network control for position tracking of a two-axis inverted pendulum system: Experimental studies. IEEE Trans. Neural Networ. 2007, 18, 1042–1048. [Google Scholar] [CrossRef]
- Chu, T.-D.; Chen, C.-K. Design and implementation of model predictive control for a gyroscopic inverted pendulum. Appl. Sci. 2017, 7, 1272. [Google Scholar] [CrossRef] [Green Version]
- Jin, S.; Ou, Y. A wheeled inverted pendulum learning stable and accurate control from demonstrations. Appl. Sci. 2019, 9, 5279. [Google Scholar] [CrossRef] [Green Version]
- Llama, M.; Flores, A.; Garcia-Hernandez, R.; Santibañez, V. Heuristic global optimization of an adaptive fuzzy controller for the inverted pendulum system: Experimental comparison. Appl. Sci. 2020, 10, 6158. [Google Scholar] [CrossRef]
- Lin, C.-J.; Lin, X.-Y.; Jhang, J.-Y. Unstable system control using an improved particle swarm optimization-based neural n etwork controller. Electronics 2019, 8, 1302. [Google Scholar] [CrossRef] [Green Version]
- Meerkov, S. Principle of vibrational control: Theory and applications. IEEE Trans. Autom. Contr. 1980, 25, 755–762. [Google Scholar] [CrossRef]
- Meerkov, S. Condition of vibrational stabilizability for a class of nonlinear systems. IEEE Trans. Autom. Contr. 1982, 27, 485–487. [Google Scholar] [CrossRef]
- Bellman, R.; Bentsman, J.; Meerkov, S.M. Vibrational control of systems with Arrhenius dynamics. J. Math. Anal. Appl. 1983, 91, 152–191. [Google Scholar] [CrossRef] [Green Version]
- Bellman, R.; Bentsman, J.; Meerkov, S. On vibrational stabilizability of nonlinear systems. J. Optim. Theory App. 1985, 46, 421–430. [Google Scholar] [CrossRef] [Green Version]
- Bellman, R.; Bentsman, J.; Meerkov, S. Vibrational control of nonlinear systems: Vibrational stabilizability. IEEE Trans. Autom. Contr. 1986, 31, 710–716. [Google Scholar] [CrossRef]
- Bellman, R.; Bentsman, J.; Meerkov, S. Vibrational control of nonlinear systems: Vibrational controllability and transient behavior. IEEE Trans. Autom. Contr. 1986, 31, 717–724. [Google Scholar] [CrossRef]
- Berg, J.M.; Wickramasinghe, I.M. Vibrational control without averaging. Automatica 2015, 58, 72–81. [Google Scholar] [CrossRef]
- Brockett, R.W. On the rectification of vibratory motion. Sens. Actuat. 1989, 20, 91–96. [Google Scholar] [CrossRef]
- Blackburn, J.A.; Smith, H.; Grønbech-Jensen, N. Stability and Hopf bifurcations in an inverted pendulum. Am. J. Phys. 1992, 60, 903–908. [Google Scholar] [CrossRef]
- Levi, M.; Weckesser, W. Stabilization of the inverted linearized pendulum by high frequency vibrations. SIAM Rev. 1995, 37, 219–223. [Google Scholar] [CrossRef]
- Bullo, F. Averaging and vibrational control of mechanical systems. SIAM J. Control. Optim. 2002, 41, 542–562. [Google Scholar] [CrossRef] [Green Version]
- Seyranian, A.; Seyranian, A. The stability of an inverted pendulum with a vibrating suspension point. J. Appl. Math. Mech. 2006, 70, 754–761. [Google Scholar] [CrossRef]
- Horton, B.; Wiercigroch, M.; Xu, X. Transient tumbling chaos and damping identification for parametric pendulum. Phil. Trans. R. Soc. A 2008, 366, 767–784. [Google Scholar] [CrossRef]
- Nandakumar, K.; Wiercigroch, M.; Chatterjee, A. Optimum energy extraction from rotational motion in a parametrically excited pendulum. Mech. Res. Commun. 2012, 43, 7–14. [Google Scholar] [CrossRef]
- Yurchenko, D.; Alevras, P. Dynamics of the N-pendulum and its application to a wave energy converter concept. Int. J. Dyn. Contr. 2013, 1, 290–299. [Google Scholar] [CrossRef] [Green Version]
- Reguera, F.; Dotti, F.E.; Machado, S.P. Rotation control of a parametrically excited pendulum by adjusting its length. Mech. Res. Commun. 2016, 72, 74–80. [Google Scholar] [CrossRef]
- Landu, L.D.; Lifshitz, E.M. Mechanics; Pergamon Press: Oxford, UK, 1960; Volume 8. [Google Scholar]
- Capecchi, D.; Bishop, S.R. Periodic oscillations and attracting basins for a parametrically excited pendulum. Int. J. Dyn. Stab. Syst. 1994, 9, 123–143. [Google Scholar] [CrossRef]
- Erdos, G.; Singh, T. Stability of a parametrically excited damped inverted pendulum. J. Sound Vib. 1996, 198, 643–650. [Google Scholar] [CrossRef]
- Sudor, D.J.; Bishop, S.R. Inverted dynamics of a tilted parametric pendulum. Eur. J. Mech. A Solids 1999, 18, 517–526. [Google Scholar] [CrossRef]
- Hsu, C. The response of a parametrically excited hanging string in fluid. J. Sound Vib. 1975, 39, 305–316. [Google Scholar] [CrossRef]
- Park, H.-I.; Jung, D.-H. A finite element method for dynamic analysis of long slender marine structures under combined parametric and forcing excitations. Ocean Eng. 2002, 29, 1313–1325. [Google Scholar] [CrossRef]
- Prado, F.S.; Sakamoto, F.Y.; Mazzilli, C.E. An analysis of parametric instability of risers. Lat. Am. J. Solids Struct. 2014, 11, 348–368. [Google Scholar] [CrossRef] [Green Version]
- Lou, M.; Hu, P.; Qi, X.; Li, H. Stability analysis of deepwater compliant vertical access riser about parametric excitation. Int. J. Nav. 2019, 11, 688–698. [Google Scholar] [CrossRef]
- McLain, T.W. Modeling of Underwater Manipulator Hydrodynamics with Application to the Coordinated Control of an Arm/Vehicle System. Ph.D. Thesis, Department of Mechanical Engineering, Stanford University, Stanford, CA, USA, 1996. [Google Scholar]
- Rahman, M.; Bhatta, D. Evaluation of added mass and damping coefficient of an oscillating circular cylinder. Appl. Math. Model. 1993, 17, 70–79. [Google Scholar] [CrossRef]
- Lin, C.C.; Chen, R.C.; Li, T.L. Experimental determination of the hydrodynamic coefficients of an underwater manipulator. J. Robot. Syst. 1999, 16, 329–338. [Google Scholar] [CrossRef]








| No. | Quantities | Values |
|---|---|---|
| 1 | Mass, mr (Kg) | 0.165 |
| 2 | Length, l (m) | 1 |
| 3 | Diameter, d (m) | 0.01 |
| 4 | Gravitational force, g (m/s2) | 9.81 |
| 5 | Coefficient of drag force, CD | 1.28 |
| 6 | Coefficient of added mass, Ca | 2.0 |
| 7 | Water density ρw, (Kg/m3) | 1000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasnain, S.; Kallu, K.D.; Nawaz, M.H.; Abbas, N.; Pruncu, C.I. Dynamic Response of an Inverted Pendulum System in Water under Parametric Excitations for Energy Harvesting: A Conceptual Approach. Energies 2020, 13, 5215. https://doi.org/10.3390/en13195215
Hasnain S, Kallu KD, Nawaz MH, Abbas N, Pruncu CI. Dynamic Response of an Inverted Pendulum System in Water under Parametric Excitations for Energy Harvesting: A Conceptual Approach. Energies. 2020; 13(19):5215. https://doi.org/10.3390/en13195215
Chicago/Turabian StyleHasnain, Saqib, Karam Dad Kallu, Muhammad Haq Nawaz, Naseem Abbas, and Catalin Iulin Pruncu. 2020. "Dynamic Response of an Inverted Pendulum System in Water under Parametric Excitations for Energy Harvesting: A Conceptual Approach" Energies 13, no. 19: 5215. https://doi.org/10.3390/en13195215
APA StyleHasnain, S., Kallu, K. D., Nawaz, M. H., Abbas, N., & Pruncu, C. I. (2020). Dynamic Response of an Inverted Pendulum System in Water under Parametric Excitations for Energy Harvesting: A Conceptual Approach. Energies, 13(19), 5215. https://doi.org/10.3390/en13195215