Neural Network-Based Supplementary Frequency Controller for a DFIG Wind Farm
Abstract
:1. Introduction
- The effects of load disturbance, percentage of wind penetration, and wind speed on the optimal droop gain are investigated.
- The designed ANN-based frequency controller can yield the desired droop gain in a very efficient manner. Thus, it is suitable for real-time applications.
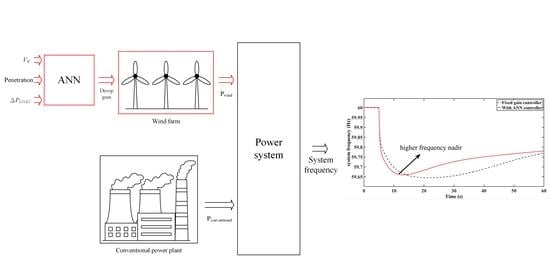
- The proposed ANN-based frequency controller can give a better frequency response than the fixed-gain controller. In addition, the ANN can yield controller gains that are very close to the optimal gains, even when the input variables such as wind speed, wind penetration, and load disturbance are not included in the training patterns of the ANN.
2. System Model
3. Effect of Load Disturbance, Wind Power Penetration, and Wind Speed on the Optimal Controller Gain
3.1. Effect of Load Disturbance ΔPLoad on the Optimal Gain KPD
3.2. Effect of the Percentage of Wind Penetration on the Optimal Gain KPD
3.3. Effect of the Percentage of Wind Speed on the Optimal Gain KPD
4. ANN-Based Frequency Controller
- Step 1
- Set the , wind power penetration, and that are considered in this work and the minimum value of the .
- Step 2
- Solve the dynamic frequency response of the system using the nonlinear model in Figure 1.
- Step 3
- If the dynamic response satisfies the requirements defined in Equation (3), record the and the frequency nadir.
- Step 4
- Find the that gives the highest frequency nadir under different scenarios and record the , wind power penetration, , and .
5. Case Studies
5.1. Comparison of ANN-Based Controller and Fixed-Gain Controller under Different Load Disturbances
5.2. Comparison of the ANN-Based Controller and Fixed-Gain Controller under Different Wind Power Penetrations
5.3. Comparison of the ANN-Based Controller and Fixed-Gain Controller under Different Wind Speeds
5.4. ANN Performance Test for Untrained Cases
5.5. Feasible Operating Regions for the ANN-Based Controller
6. Conclusions
- The droop gain decreases with the increasing magnitude of the load disturbances.
- The droop gain should be increased when the wind power penetration is increased.
- The droop gain increases with the increasing wind speed.
- The ANN-based controller yields essentially the same droop gain as the optimal controller using the exhaustive search method. However, the ANN-based method is more efficient than the exhaustive search method, since time-consuming simulations can be avoided after the ANN is trained. Therefore, the ANN-based controller can be used in online applications, and the optimal controller using the exhaustive search method cannot be employed for real-time applications.
- A major feature of the ANN-based controller is that it can be employed to provide the desired droop gain without the need to perform additional simulations, even when the load disturbance, wind penetration, and wind speed are not within the set of training patterns.
- By using the ANN-based controller with different gains under different operating conditions, the feasible operating regions under different wind speeds and different wind penetrations can be expanded.
- In practical applications, the load disturbance can be estimated from the rate of change of frequency (). The wind penetration is computed using the rated capacities of online units. The wind speed is assumed to be available at the local wind farm.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| D | load damping |
| equivalent inertia time constants of synchronous machine and DFIG | |
| nominal frequency and system frequency | |
| power fractions of the high, intermediate, and low-pressure turbines | |
| maximum power point tracking constant | |
| DFIG supplementary proportional controller gain | |
| synchronous machine droop and integral controller gains | |
| control signal, speed relay output signal, and steam valve position of the synchronous machine | |
| mechanical output power of the high, intermediate, and low-pressure turbines | |
| Load demand | |
| electromagnetic power of DFIG | |
| mechanical power of synchronous machine | |
| speed relay and servo-motor time constants of the synchronous machine | |
| steam chest, reheater, and crossover time constants of the synchronous machine | |
| mechanical torque and electromagnetic torque of DFIG | |
| electromagnetic torque command of DFIG for MPPT operation | |
| DFIG torque command | |
| DFIG speed | |
| wind speed | |
| wind turbine power coefficient | |
| area swept by the wind turbine blades | |
| air density | |
| wind turbine tip speed ratio and blade pitch angle | |
| incremental quantity |
Appendix A
References
- Bureau of Energy, Ministry of Economic Affairs, Wind Power Generation Four Years Project. Taiwan, August 2017. Available online: https://www.moeaboe.gov.tw/ECW/populace/content/ContentDesc.aspx?menu_id=5493 (accessed on 12 October 2020).
- Shahabi, M.; Haghifam, M.R.; Mohamadian, M.; Nabavi-Niaki, S.A. Microgrid dynamic performance improvement using a doubly fed induction wind generator. IEEE Trans. Energy Convers. 2009, 24, 137–145. [Google Scholar] [CrossRef]
- Lee, J.; Jang, G.; Muljadi, E.; Blaabjerg, F.; Chen, Z.; Kang, Y.C. Stable short-term frequency support using adaptive gains for a DFIG-based wind power plant. IEEE Trans. Energy Convers. 2016, 31, 1068–1079. [Google Scholar] [CrossRef]
- Arani, M.F.M.; Mohamed, Y.A.I. Analysis and impacts of implementing droop control in DFIG-based wind turbines on microgrid/weak-grid stability. IEEE Trans. Power Syst. 2015, 30, 385–396. [Google Scholar] [CrossRef]
- Arani, M.F.M.; Mohamed, Y.A.I. Dynamic droop control for wind turbines participating in primary frequency regulation in microgrids. IEEE Trans. Smart Grid 2018, 9, 5742–5751. [Google Scholar] [CrossRef]
- Yang, J.; Chen, Y.; Hsu, Y. Small-signal stability analysis and particle swarm optimisation self-tuning frequency control for an islanding system with DFIG wind farm. IET Gener. Transm. Distrib. 2019, 13, 563–574. [Google Scholar] [CrossRef]
- Hwang, M.; Muljadi, E.; Park, J.; Sørensen, P.; Kang, Y.C. Dynamic droop-based inertial control of a doubly-fed induction generator. IEEE Trans. Sustain. Energy 2016, 7, 924–933. [Google Scholar] [CrossRef]
- Vidyanandan, K.V.; Senroy, N. Primary frequency regulation by deloaded wind turbines using variable droop. IEEE Trans. Power Syst. 2013, 28, 837–846. [Google Scholar] [CrossRef]
- Ramtharan, G.; Ekanayake, J.B.; Jenkins, N. Frequency support from doubly fed induction generator wind turbines. IET Renew. Power Gener. 2007, 1, 3–9. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Z.; Zhang, J.; Wong, K.P. Variable gain control scheme of DFIG-based wind farm for over-frequency support. Renew. Energy 2018, 120, 379–391. [Google Scholar] [CrossRef]
- Pradhan, C.; Bhende, C.N.; Samanta, A.K. Adaptive virtual inertia-based frequency regulation in wind power systems. Renew. Energy 2018, 115, 558–574. [Google Scholar] [CrossRef]
- Ochoa, D.; Martinez, S. Frequency dependent strategy for mitigating wind power fluctuations of a doubly-fed induction generator wind turbine based on virtual inertia control and blade pitch angle regulation. Renew. Energy 2018, 128, 108–124. [Google Scholar]
- Camblong, H.; Vechiu, I.; Guillaud, X.; Etxeberria, A.; Kreckelbergh, S. Wind turbine controller comparison on an island grid in terms of frequency control and mechanical stress. Renew. Energy 2014, 63, 37–45. [Google Scholar] [CrossRef]
- Papaefthymiou, S.V.; Lakiotis, V.G.; Margaris, I.D.; Papathanassiou, S.A. Dynamic analysis of island systems with wind-pumped-storage hybrid power stations. Renew. Energy 2015, 74, 544–554. [Google Scholar] [CrossRef]
- Mauricio, J.M.; Marano, A.; Gomez-Exposito, A.; Ramos, J.L.M. Frequency regulation contribution through variable-speed wind energy conversion systems. IEEE Trans. Power Syst. 2009, 24, 173–180. [Google Scholar] [CrossRef]
- Kayikci, M.; Milanovic, J.V. Dynamic contribution of DFIG-based wind plants to system frequency disturbances. IEEE Trans. Power Syst. 2009, 24, 859–867. [Google Scholar] [CrossRef]
- Margaris, I.D.; Papathanassiou, S.A.; Hatziargyriou, N.D.; Hansen, A.D.; Sorensen, P. Frequency control in autonomous power systems with high wind power penetration. IEEE Trans. Sustain. Energy 2012, 3, 189–199. [Google Scholar]
- Vyver, J.V.D.; Kooning, J.D.M.D.; Meersman, B.; Vandevelde, L.; Vandoorn, T.L. Droop control as an alternative inertial response strategy for the synthetic inertia on wind turbines. IEEE Trans. Power Syst. 2016, 31, 1129–1138. [Google Scholar] [CrossRef]
- Wilches-Bernal, F.; Chow, J.H.; Sanchez-Gasca, J.J. A fundamental study of applying wind turbines for power system frequency control. IEEE Trans. Power Syst. 2016, 31, 1496–1505. [Google Scholar] [CrossRef]
- Hafiz, F.; Abdennour, A. An adaptive neuro-fuzzy inertia controller for variable-speed wind turbines. Renew. Energy 2016, 92, 136–146. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines, 3rd ed.; Pearson: Upper Saddle River City, NJ, USA, 2008. [Google Scholar]
- Taiwan Power Company. Power System Operation Guide; Taiwan Power Company: Taipei City, Taiwan, 2020. [Google Scholar]
- Zhang, Z.; Sun, Y.; Lin, J.; Li, G. Coordinated frequency regulation by doubly fed induction generator-based wind power plants. IET Renew. Power Gener. 2012, 6, 38–47. [Google Scholar] [CrossRef]
















© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chien, T.-H.; Huang, Y.-C.; Hsu, Y.-Y. Neural Network-Based Supplementary Frequency Controller for a DFIG Wind Farm. Energies 2020, 13, 5320. https://doi.org/10.3390/en13205320
Chien T-H, Huang Y-C, Hsu Y-Y. Neural Network-Based Supplementary Frequency Controller for a DFIG Wind Farm. Energies. 2020; 13(20):5320. https://doi.org/10.3390/en13205320
Chicago/Turabian StyleChien, Ting-Hsuan, Yu-Chuan Huang, and Yuan-Yih Hsu. 2020. "Neural Network-Based Supplementary Frequency Controller for a DFIG Wind Farm" Energies 13, no. 20: 5320. https://doi.org/10.3390/en13205320
APA StyleChien, T.-H., Huang, Y.-C., & Hsu, Y.-Y. (2020). Neural Network-Based Supplementary Frequency Controller for a DFIG Wind Farm. Energies, 13(20), 5320. https://doi.org/10.3390/en13205320