Self-Reinforcing Electricity Price Dynamics under the Variable Market Premium Scheme
Abstract
:1. Introduction
2. Methods
2.1. Plain Mathematical Model
2.2. Agent-Based Simulation
3. Results
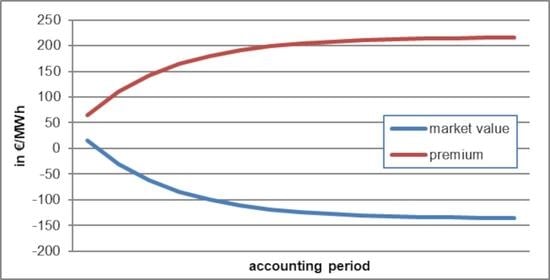
3.1. Results from Plain Mathematical Modeling
3.1.1. Case 1: No Market Impact
3.1.2. Case 2: Moderate Market Influence
3.1.3. Case 3: Significant Market Distortion
3.2. Results from the Agent-Based Simulation
3.2.1. Results for the Simple Scenario
3.2.2. Results for the Extended Scenario
4. Discussion
- … is an artefact of the simulation itself (Objection A);
- … is attenuated by other influences (Objection B);
- … is already addressed by current regulations (Objection C).
4.1. Objection A—Is the Effect a Model Artefact?
4.2. Objection B—Is the Effect Attenuated by Other Influences?
4.3. Objection C—Is the Effect Addressed by Current Regulations?
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Details on AMIRIS

Appendix A.2. Scenario with High Wind Capacities
| Technology | Capacity/GW |
|---|---|
| Photovoltaics | 100 |
| Wind Onshore | 180 |
| Wind Offshore | 40 |
| Gas CC | 35 |
| Gas Turbine | 20 |
| Hard Coal | 15 |
| Lignite | 10 |
| Storage 1 | 20 |



Appendix A.3. Scenario with High Storage Capacities
| Technology | Capacity/GW |
|---|---|
| Photovoltaics | 200 |
| Wind Onshore | 80 |
| Wind Offshore | 20 |
| Gas CC | 35 |
| Gas Turbine | 20 |
| Hard Coal | 15 |
| Lignite | 10 |
| Storage 1 | 40 |



References
- BMWi. Zeitreihen zur Entwicklung der Erneuerbaren Energien in Deutschland 1990–2018; Bundesministerium für Wirtschaft und Energie: Berlin, Germany, 2019. [Google Scholar]
- IEA. World Energy Outlook 2019. 2019. Available online: https://www.iea.org/reports/world-energy-outlook-2019 (accessed on 8 October 2020).
- Eurostat. Eurostat European Statistics Database; Eurostat: London, UK, 2018. [Google Scholar]
- Teske, S. Achieving the Paris Climate Agreement Goals: Global and Regional 100% Renewable Energy Scenarios to Achieve the Paris Agreement Goals with Non-Energy GHG Pathways for +1.5 °C and +2 °C; Springer: Cham, Germany, 2019. [Google Scholar]
- Jacobson, M.Z.; Delucci, M.A.; Bauer, Z.A.F.; Goodman, S.C.; Erwin, J.R.; Fobi, S.N.; Liu, J.; Lo, J.; Meyer, C.B.; Morris, S.B.; et al. 100% Clean and Renewable Wind, Water, and Sunlight All-Sector Energy Roadmaps for 139 Countries in the World. Joule 2017, 1, 108–121. [Google Scholar] [CrossRef] [Green Version]
- Brown, T.W.; Blok, K.; Breyer, C.; Lund, H.; Mathiesen, B.V. Response to ‘Burden of proof: A comprehensive review of the feasibility of 100% renewable-electricity systems’. Renew. Sustain. Energy Rev. 2018, 92, 834–847. [Google Scholar] [CrossRef]
- Winkler, J.; Giao, A.; Pfluger, B.; Ragwitz, M. Impact of renewables on electricity markets—Do support schemes matter? Energy Policy 2016, 93, 157–167. [Google Scholar] [CrossRef]
- Purkus, A.; Gawel, E.; Deissenroth, M.; Nienhaus, K.; Wassermann, S. Market integration of renewable energies through direct marketing—Lessons learned from the German market premium scheme. Energy Sustain. Soc. 2015, 5. [Google Scholar] [CrossRef] [Green Version]
- Alberici, S.; Boeve, S.; Deng, Y.; Wouters, K.; Winkei, T. Subsidies and Costs of EU Energy: Final Report. 2014. Available online: https://ec.europa.eu/energy/sites/ener/files/documents/ECOFYS%202014%20Subsidies%20and%20costs%20of%20EU%20energy_11_Nov.pdf (accessed on 8 October 2020).
- Mora, D. Auctions for Renewable Energy Support—Taming the Beast of Competitive Bidding: Final Report of the AURES Project. 2017. Available online: http://auresproject.eu/sites/aures.eu/files/media/documents/aures-finalreport.pdf (accessed on 8 October 2020).
- RESLEGAL. RES LEGAL Europe Comparison Tool. 2020. Available online: http://www.res-legal.eu/ (accessed on 8 October 2020).
- REN. Renewables 2017 Global Status Report. 2017. Available online: http://www.ren21.net/status-of-renewables/global-status-report/ (accessed on 8 October 2020).
- Klobasa, M.; Ragwitz, M. Market Integration of Renewable Electricity Generation—The German Market. Premium Model. Energy Environ. 2013, 24, 127–146. [Google Scholar] [CrossRef]
- Kitzing, L.; Weber, C. Support. mechanisms for renewables: How risk exposure influences investment incentives. Int. J. Sustain. Energy Plan. Manag. 2015, 7. [Google Scholar] [CrossRef] [Green Version]
- Pollitt, M.G.; Anaya, K.L. Can current electricity markets cope with high shares of renewables? A comparison of approaches in Germany, the UK and the State of New York. Energy J. 2016, 37. [Google Scholar] [CrossRef] [Green Version]
- Neuhoff, K.; May, N.; Richstein, J.C. Renewable Energy Policy in the Age of Falling Technology Costs. 2018. Available online: http://hdl.handle.net/10419/181032 (accessed on 8 October 2020).
- Visser, E.; Held, A. Methodologies for Estimating Levelised Cost of Electricity (LCOE); Ecofys: Utrecht, The Netherlands, 2014. [Google Scholar]
- Newbery, D.; Pollitt, M.G.; Ritz, R.A.; Strielkowski, W. Market design for a high-renewables European electricity system. Renew. Sustain. Energy Rev. 2018, 91, 695–707. [Google Scholar] [CrossRef] [Green Version]
- Cramton, P.; Stoft, S. Why We Need to Stick with Uniform-Price Auctions in Electricity Markets. Electr. J. 2007, 20, 26–37. [Google Scholar] [CrossRef] [Green Version]
- Blume-Werry, E.; Faber, T.; Hirth, L.; Huber, C.; Everts, M. Eyes on the Price: Which Power Generation Technologies Set the Market Price? Price Setting in European Electricity Markets: An Application to the Proposed Dutch Carbon Price Floor. 2019. Available online: https://EconPapers.repec.org/RePEc:ags:feemes:281287 (accessed on 8 October 2020).
- Torralba-Díaz, L.; Schimeczek, C.; Reeg, M.; Savvidis, G.; Deissenroth-Uhrig, M.; Guthoff, F.; Fleischer, B.; Hufendiek, K. Identification of the Efficiency Gap by Coupling a Fundamental Electricity Market Model and an Agent-Based Simulation Model. Energies 2020, 13, 3920. [Google Scholar] [CrossRef]
- Reeg, M. AMIRIS—Ein Agentenbasiertes Simulations-Modell zur Akteursspezifischen Analyse Techno-Ökonomischer und Soziotechnischer Effekte bei der Strommarktintegration und Refinanzierung Erneuerbarer Energien; Technische Universität Dresden: Dresden, Germany, 2019. [Google Scholar]
- Deissenroth, M.; Klein, M.; Reeg, M. Assessing the Plurality of Actors and Policy Interactions: Agent-Based Modelling of Renewable Energy Market Integration; John Wiley & Sons: New York, NY, USA, 2017. [Google Scholar]
- Reeg, M.; Nienhaus, K. AMIRIS—Weiterentwicklung Eines Agentenbasierten Simulationsmodells zur Untersuchung des Akteursverhaltens bei der Marktintegration von Strom aus Erneuerbaren Energien unter Verschiedenen Fördermechanismen; DLR: Stuttgart, Germany, 2013. [Google Scholar]
- Klein, M.; Frey, U.J.; Reeg, M. Models Within Models—Agent-Based Modelling and Simulation in Energy Systems Analysis. J. Artif. Soc. Soc. Simul. 2019, 22, 6. [Google Scholar] [CrossRef]
- Reeg, M. AMIRIS—An Agent-Based Simulation Model for the Actor-Specific Analysis of Techno-Economic and Socio-Technical Effects in Electricity Market Integration and Refinancing of Renewable Energies; DLR: Stuttgart, Germany, 2019; Available online: https://nbn-resolving.org/urn:nbn:de:bsz:14-qucosa2-347643 (accessed on 8 October 2020).
- OPSD. Load, Wind and Solar, Prices in Hourly Resolution. 2020. Available online: https://data.open-power-system-data.org/time_series/2019-06-05 (accessed on 8 October 2020).
- Schill, W.-P. Residual load, renewable surplus generation and storage requirements in Germany. Energy Policy 2014, 73, 65–79. [Google Scholar] [CrossRef] [Green Version]
- Sensfuß, F.; Ragwitz, M.; Genoese, M. The merit-order effect: A detailed analysis of the price effect of renewable electricity generation on spot market prices in Germany. Energy Policy 2008, 36, 3086–3094. [Google Scholar] [CrossRef] [Green Version]
- Fischer, C. How can Renewable Portfolio Standards Lower Electricity Prices; Resources for the Future Discussion; RFF DP: Washington, DC, USA, 2006; pp. 6–20. [Google Scholar]
- Coase, R.H. The Economics of Uniform Pricing Systems. Manch. Sch. 1947, 15, 139–156. [Google Scholar] [CrossRef]
- Müsgens, F.; Ockenfels, A.; Peek, M. Economics and design of balancing power markets in Germany. Int. J. Electr. Power Energy Syst. 2014, 55, 392–401. [Google Scholar] [CrossRef]
- López Prol, J.; Steininger, K.W.; Zilberman, D. The cannibalization effect of wind and solar in the California wholesale electricity market. Energy Econ. 2020, 85. [Google Scholar] [CrossRef]
- Axelrod, R.; Hamilton, W.D. The evolution of cooperation. Science 1981, 211, 1390–1396. [Google Scholar] [CrossRef] [PubMed]
- Pahle, M.; Schill, W.P.; Gambardella, C. Renewable Energy Support. Negative Prices, and Real-time Pricing. Energy J. 2016, 37. [Google Scholar] [CrossRef]
- Brunner, C.; Möst, D. The impact of different flexibility options on future electricity spot prices in Germany. In Proceedings of the 12th International Conference on the European Energy Market (EEM), Lisbon, Portugal, 19–22 May 2015. [Google Scholar]
- EEG. Gesetz für den Ausbau Erneuerbarer Energien (Erneuerbare-Energien-Gesetz (EEG) Bundesanzeiger des Bundesministeriums für Justiz; BMVJ: Rostock, Germany, 2014. [Google Scholar]
- Knight, S. Six-Hour Negative Pricing Rule Damaging Offshore Wind Revenues; Windpower Monthly: London, UK, 2020. [Google Scholar]
- InnAusV. Verordnung zu den Innovationsausschreibungen (Innovationsausschreibungsverordnung—InnAusV); BMVJ: Rostock, Germany, 2020. [Google Scholar]
- Noothout, P.; de Jager, D.; Tesnière, L.; van Rooijen, S.; Karypidis, N.; Brückmann, R.; Jirouš, F.; Breitschopf, B.; Angelopoulos, D.; Doukas, H. The Impact of Risks in Renewable Energy Investments and the Role of Smart Policies; DiaCore: Athens, Greece, 2016. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |





| Technology | Capacity in GW |
|---|---|
| Photovoltaics | 200 |
| Gas Power Plant | 120 |
| Technology | Capacity/GW |
|---|---|
| Photovoltaics | 200 |
| Wind Onshore | 80 |
| Wind Offshore | 20 |
| Gas CC | 35 |
| Gas Turbine | 20 |
| Hard Coal | 15 |
| Lignite | 10 |
| Storage 1 | 20 |
| Month | PV | WindOn | WindOff |
|---|---|---|---|
| 1 | 14% | 17% | 10% |
| 2 | 24% | 43% | 23% |
| 3 | 20% | 24% | 21% |
| 4 | 54% | 18% | 6% |
| 5 | 62% | 28% | 19% |
| 6 | 46% | 11% | 3% |
| 7 | 59% | 31% | 14% |
| 8 | 65% | 15% | 7% |
| 9 | 52% | 7% | 13% |
| 10 | 15% | 3% | 3% |
| 11 | 7% | 15% | 6% |
| 12 | 4% | 35% | 11% |
| (a) | (b) | ||||||
|---|---|---|---|---|---|---|---|
| Month | PV | WindOn | WindOff | Month | PV | WindOn | WindOff |
| 5% | 3% | 2% | 1 | 5% | 7% | 4% | |
| 2 | 9% | 3% | 0% | 2 | 0% | 1% | 0% |
| 3 | 20% | 13% | 12% | 3 | 0% | 0% | 0% |
| 4 | 19% | 0% | 0% | 4 | 21% | 9% | 0% |
| 5 | 33% | 0% | 0% | 5 | 15% | 7% | 0% |
| 6 | 25% | 0% | 0% | 6 | 15% | 6% | 0% |
| 7 | 27% | 0% | 0% | 7 | 20% | 10% | 0% |
| 8 | 35% | 0% | 0% | 8 | 18% | 6% | 0% |
| 9 | 33% | 0% | 0% | 9 | 11% | 7% | 10% |
| 10 | 1% | 0% | 0% | 10 | 12% | 3% | 3% |
| 11 | 0% | 0% | 0% | 11 | 4% | 4% | 0% |
| 12 | 4% | 3% | 3% | 12 | 0% | 17% | 0% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frey, U.J.; Klein, M.; Nienhaus, K.; Schimeczek, C. Self-Reinforcing Electricity Price Dynamics under the Variable Market Premium Scheme. Energies 2020, 13, 5350. https://doi.org/10.3390/en13205350
Frey UJ, Klein M, Nienhaus K, Schimeczek C. Self-Reinforcing Electricity Price Dynamics under the Variable Market Premium Scheme. Energies. 2020; 13(20):5350. https://doi.org/10.3390/en13205350
Chicago/Turabian StyleFrey, Ulrich J., Martin Klein, Kristina Nienhaus, and Christoph Schimeczek. 2020. "Self-Reinforcing Electricity Price Dynamics under the Variable Market Premium Scheme" Energies 13, no. 20: 5350. https://doi.org/10.3390/en13205350
APA StyleFrey, U. J., Klein, M., Nienhaus, K., & Schimeczek, C. (2020). Self-Reinforcing Electricity Price Dynamics under the Variable Market Premium Scheme. Energies, 13(20), 5350. https://doi.org/10.3390/en13205350