Neural Methods Comparison for Prediction of Heating Energy Based on Few Hundreds Enhanced Buildings in Four Season’s Climate
Abstract
:1. Introduction
1.1. Scientific Context and Recent Trends in through Data-Driven Modeling
1.2. Habitat Thermal Comfort Versus Cognitive and Emotional Dissonance
2. Critical Bibliographical Analysis of Estimation Methods for Building’s Energy Demand
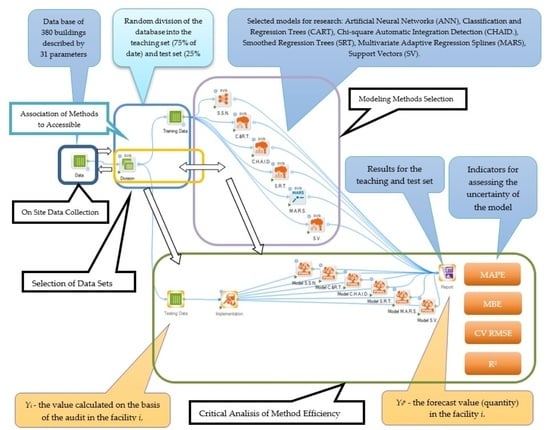
3. Proposed Methodology of Investigations—Experimental Sites and Structure Model
- the “construction technology”,
- the “geometry” of the building”,
- the “meteorological” environmental conditions, and
- the “preferences” of their inhabitants.
4. Description of Research Methodology and Application
5. Results and Discussion
6. Conclusions and Perspectives
- When assessing the quality of individual methods solely on the basis of the MAPE index (the index most frequently used for assessment) determined for the test set, it can be said that the best quality energy consumption forecasts after thermal rehabilitation were obtained by SRT and ANN methods, for which it was necessary to use the data from the V set as input variables. The error value was 12.1% and 12.5% respectively. Slightly worse quality forecasts, because they were burdened with a MAPE error of 14%, were obtained for the IV set of input variables and methods ANN, MARS, and SRT.
- When evaluating the methods according to the indicators proposed by ASHARE, the SV model together with IV and V sets of input variables should be considered the best in terms of MBE error. Slightly worse results, at the error level of about 4%, were obtained for the two best methods in terms of MAPE error, i.e., ANN and SRT and CHID and MARS methods. Unfortunately, CHID and SV methods were characterized by twice as high RMSE CV error as the other indicated methods. Also, the correlation coefficient for them did not meet the assumed assumptions, as it was only 0.3–0.6.
- Taking into account all quality assessment indicators, the ANN models should be indicated as preferred, together with an IV or V set of independent variables. For these sets of variables, the use of SRT models, followed by MARS, can also be considered. These models were in most cases burdened with only slightly larger errors.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| ANN | Artificial Neural Network |
| CART | Classification and Regression Tree |
| CHAID | Chi-square Automatic Interaction Detector |
| CV RSME | Coefficient of Variance of the Root Mean Square Error, [%] |
| MAPE | Mean Absolute Percentage Error, [%] |
| MARS | Multivariate Adaptive Regression Splines |
| MBE | Mean Bias Error, [%] |
| R2 | Coefficient of determination |
| SRT | Support Regression Trees |
| SV | Support Vectors |
| Af | calculated surface of heated floors from interior measurements, [m2] |
| Afl | calculated surface of floor from interior measurements (floor over basement or floor on the ground), [m2] |
| Ain | calculated from interior measurements total (net internal area), [m2] |
| Ar | calculated from exterior measurements surface of roof projection area (net), [m2] |
| Atw | calculated from exterior measurements total windows area, [m2] |
| Aw | calculated from exterior measurements total walls’ surface (net) area, [m2] |
| CA | construction year of a building, [year] |
| FE0 | final energy demand for heating and domestic hot water before modernization, [kWh∙m−2·year−1] |
| FE1 | final energy demand for heating and domestic hot water after modernization, [kWh∙m−2·year−1] |
| m | number of objects |
| Nop | number of residential flats, premises, [pc.] |
| Nopb | number of living persons per building, [Nb] |
| Nos | number of stores, [pc.] |
| Qh | measured, consumed annual energy for heating, [GJ∙year−1] |
| Qr,h+ww | measured, annual heat consumption for building heating converted to the conditions of the standard heating season + energy for hot water provision, [GJ∙year−1] |
| Qww | measured, consumed annual energy for hot water provision, [GJ∙year−1] |
| S/Ve | shape coefficient of buildings (the ratio surface to volume), [m2∙m−3], [m−1] |
| Uf | calculated thermal transmittance of floors components (floor over basement), [W∙m2·K−1] |
| Ug | calculated thermal transmittance of floor components on the ground, [W∙m−2·K−1] |
| Upw | calculated thermal transmittance of peak walls components, [W∙m−2·K−1] |
| Ur | calculated thermal transmittance of roof projections components, [W∙m−2·K−1] |
| Uw | calculated thermal transmittance of walls components, [W∙m−2·K−1] |
| Uwin | ansmittance of windows (commercial data), [W∙m−2·K−1] |
| Ve | calculated from exterior measurements the heated volume of building, [m3] |
| yi | the actual quantity in the facility i |
| ypi | the forecast quantity in the facility i |
| Φh | calculated heating consumed power, [kW] |
References
- Reckel, P. Effet de Serres Sur le €O2. 2040 Quel Climat en France Métropolitaine; Amazon: Paris, France, 2019. [Google Scholar]
- Frezal, B.; Leininger-Frezal, C.; Mathia, T.G.; Mory, B. Influence et Systèmes–Introduction Provisoire à la Théorie de L’Influence et de la Manipulation; L’Interdisciplinaire: Québec, QC, Canada, 2011. [Google Scholar]
- Bourdeau, M.; Zhai, X.-Q.; Nefzaoui, E.; Guo, X.; Chatellier, P. Modelling and forecasting building energy consumption: A review of data-driven techniques. Sustain. Cities Soc. 2019, 48, 101533. [Google Scholar] [CrossRef]
- Dong, B.; Li, Z.; Rahman, S.M.M.; Vega, R. A hybrid model approach for forecasting future residential electricity consumption. Energy Build. 2016, 117, 341–351. [Google Scholar] [CrossRef]
- ASHRAE. ASHRAE Handbook–Fundamentals—Energy Estimation and Modeling Methods, 6th ed.; American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc. (ASHRAE): Atlanta, GA, USA, 2009; ISBN 978-1-61583-170-8. Available online: https://app.knovel.com/web/toc.v/cid:kpASHRAE37/viewerType:toc/ (accessed on 5 November 2019).
- Zhao, H.; Magoulès, F. A review on the prediction of building energy consumption. Renew. Sustain. Energy Rev. 2012, 16, 3586–3592. [Google Scholar] [CrossRef]
- Szul, T.; Kokoszka, S. Application of Rough Set Theory (RST) to forecast energy consumption in buildings undergoing thermal modernization. Energies 2020, 13, 1309. [Google Scholar] [CrossRef] [Green Version]
- CEN. Energy Performance of Buildings. Ventilation for Buildings. Indoor Environmental Input Parameters for Design and Assessment of Energy Performance of Buildings Addressing Indoor Air Quality, Thermal Environment, Lighting and Acoustics. Module M1-6; ISO 16798-1:2019-06. Available online: https://standards.globalspec.com/std/14317955/bs-en-16798-1-tc (accessed on 23 September 2020).
- Costanzoa, V.; Fabbrib, K.; Piraccini, S. Stressing the passive behavior of a Passivhaus: An evidence-based scenario analysis for a Mediterranean case study. Build. Environ. 2018, 142, 265–277. [Google Scholar] [CrossRef]
- Djamila, H. Indoor thermal comfort predictions: Selected issues and trends. Renew. Sustain. Energy Rev. 2017, 74, 569–580. [Google Scholar] [CrossRef]
- Wang, Y.; Kuckelkorn, J.; Zhao, F.-Y.; Spliethoff, H.; Lang, W. A state of art of review on interactions between energy performance and indoor environment quality in Passive House buildings. Renew. Sustain. Energy Rev. 2017, 72, 1303–1319. [Google Scholar] [CrossRef]
- CEN. European Standard: Energy Performance of Buildings-Calculation of Energy Use for Space Heating and Cooling; ISO 13790:2008. 2008. Available online: https://www.iso.org/standard/41974.html (accessed on 5 November 2019).
- CEN. European Standard: Heating Systems in Buildings; ISO 12831-1:2017-08. 2017. Available online: https://sklep.pkn.pl/pn-en-12831-3-2017-08e.html (accessed on 17 November 2019).
- Ballarini, I.; Corrado, V. Application of energy rating methods to the existing building stock. Analysis of some residential buildings in Turin. Energy Build. 2009, 4, 790–800. [Google Scholar] [CrossRef]
- Crawley, D.B.; Lawrie, L.K.; Winkelmann, F.C.; Buhl, W.F.; Huang, Y.J.; Pedersen, C.O.; Strand, R.K.; Liesen, R.J.; Fisher, D.E.; Witte, M.J.; et al. Energyplus: Creating a new-generation building energy simulation program. Energy Build. 2001, 33, 319–331. [Google Scholar] [CrossRef]
- Rivers, N.; Jaccard, M. Combining top-down and bottom-up approaches to energy–economy modeling using discrete choice methods. Energy J. 2005, 26, 83–106. [Google Scholar] [CrossRef] [Green Version]
- Allard, I.; Olofsson, T.; Hassan, O.A.B. Methods for energy analysis of residential buildings in Nordic countries. Renew. Sustain. Energy Rev. 2013, 22, 306–318. [Google Scholar] [CrossRef]
- Asadi, S.; Amiri, S.S.; Mottahedi, M. On the development of multi-linear regression analysis to assess energy consumption in the early stages of building design. Energy Build. 2014, 85, 246–255. [Google Scholar] [CrossRef]
- Asadi, S.; Marwa, H.; Beheshti, A. Development and validation of a simple estimating tool to predict heating and cooling energy demand for attics of residential buildings. Energy Build. 2012, 54, 12–21. [Google Scholar] [CrossRef]
- Caldera, M.; Corgnati, S.P.; Filippi, M. Energy demand for space heating through a statistical approach: Application to residential buildings. Energy Build. 2008, 40, 1972–1983. [Google Scholar] [CrossRef]
- Chou, J.S.; Bui, D.K. Modeling heating and cooling loads by artificial intelligence for energy-efficient building design. Energy Build. 2014, 82, 437–446. [Google Scholar] [CrossRef]
- Fumo, N.; Biswas, R. Regression analysis for prediction of residential energy consumption. Renew. Sustain. Energy Rev. 2015, 47, 332–343. [Google Scholar] [CrossRef]
- Lü, X.; Lu, T.; Kibert, C.J.; Viljanen, M. Modeling and forecasting energy consumption for heterogeneous buildings using a physical–statistical approach. Appl. Energy 2015, 144, 261–275. [Google Scholar] [CrossRef]
- Ma, Z.; Li, H.; Sun, Q.; Wang, C.; Yan, A.; Starfelt, F. Statistical analysis of energy consumption patterns on the heat demand of buildings in district heating systems. Energy Build. 2014, 85, 464–472. [Google Scholar] [CrossRef]
- Praznik, M.; Butala, V.; Zbašnik-Senegačnik, M. Simplified evaluation method for energy efficiency in single-family houses using key quality parameters. Energy Build. 2013, 67, 489–499. [Google Scholar] [CrossRef]
- Sekhar-Roy, S.; Roy, R.; Balas, V.E. Estimating heating load in buildings using multivariate adaptive regression splines, extreme learning machine, a hybrid model of mars and elm. Renew. Sustain. Energy Rev. 2018, 82, 4256–4268. [Google Scholar] [CrossRef]
- Tiberiu, C.; Virgone, J.; Blanco, E. Development and validation of regression models to predict monthly heating demand for residential buildings. Energy Build. 2008, 40, 1825–1832. [Google Scholar] [CrossRef]
- Tsanas, A.; Xifara, A. Accurate quantitative estimation of energy performance of residential buildings using statistical machine learning to OLS. Energy Build. 2012, 49, 560–567. [Google Scholar] [CrossRef]
- Biswas, M.; Robinson, M.D.; Fumo, N. Prediction of residential building energy consumption: A neural network approach. Energy 2016, 117, 84–92. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Wadsworth & Brooks/Cole Advanced Books & Software: Monterey, CA, USA, 1984. [Google Scholar]
- Ekici, B.B.; Aksoy, U.T. Prediction of building energy consumption by using artificial neural networks. Adv. Eng. Softw. 2009, 40, 356–362. [Google Scholar] [CrossRef]
- Li, K.; Sua, H.; Chua, J. Forecasting building energy consumption using neural networks and hybrid neuro-fuzzy system: A comparative study. Energy Build. 2011, 43, 2893–2899. [Google Scholar] [CrossRef]
- Kumar, R.; Aggarwal, R.K.; Sharma, J.D. Energy analysis of a building using artificial neural network: A review. Energy Build. 2013, 65, 352–358. [Google Scholar] [CrossRef]
- Seyedzadeh, S.; Rahimian, F.; Glesk, I.; Roper, M. Machine learning for estimation of building energy consumption and performance: A review. Vis. Eng. 2018, 6, 5. [Google Scholar] [CrossRef]
- Ripley, B.D. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, UK, 1996; ISBN 0-521-46086-7. [Google Scholar]
- Kass, G.V. An exploratory technique for investigating large quantities of categorical data. Appl. Stat. 1980, 29, 119–127. [Google Scholar] [CrossRef]
- Friedman, J. Multivariate adaptive regression splines (with discussion). Ann. Stat. 1991, 19, 1–141. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2001. [Google Scholar]
- CEN. Performance in Construction-Determination and Calculation of Surface and Volume Indicators. ISO 9836:1997. Available online: https://www.iso.org/standard/73149.html (accessed on 7 November 2019).
- CEN. Building Components and Building Elements—Thermal Resistance and Thermal Transmittance—Calculation Methods. ISO 6946:2017-10. Available online: https://www.iso.org/standard/65708.html (accessed on 9 November 2019).
- American Society of Heating, Ventilating, and Air Conditioning Engineers (ASHRAE). Guideline 14-2014, Measurement of Energy and Demand Savings; Technical Report; American Society of Heating, Ventilating, and Air Conditioning Engineers: Atlanta, GA, USA, 2014. [Google Scholar]
- Ruiz, G.R.; Bandera, C.R. Validation of Calibrated Energy Models: Common Errors. Energies 2017, 10, 1587. [Google Scholar] [CrossRef] [Green Version]
- Webster, L.; Bradford, J.; Sartor, D.; Shonder, J.; Atkin, E.; Dunnivant, S.; Frank, D.; Franconi, E.; Jump, D.; Schiller, S.; et al. M&V Guidelines: Measurement and Verification for Performance-Based Contracts; Version 4.0, Technical Report; U.S. Department of Energy Federal Energy Management Program: Washington, DC, USA, 2015.






| No. | Parameter | Abbreviation | Average | Median |
|---|---|---|---|---|
| 1 | construction year of a building, [year] | CA | 1970 | 1971 |
| 2 | calculated from exterior measurements the heated volume of building, [m3] | Ve | 6393.1 | 5409.4 |
| 3 | calculated from interior measurements total (net internal area), [m2] | Ain | 1764.0 | 1565.8 |
| 4 | calculated surface of heated floors from interior measurements, [m2] | Af | 1568.5 | 1523.8 |
| 5 | calculated from exterior measurements surface of roof projection area (net), [m2] | Ar | 467.0 | 382.2 |
| 6 | calculated from exterior measurements total walls’ surface (net) area, [m2] | Aw | 1096.8 | 979.4 |
| 7 | calculated surface of floor from interior measurements (floor over basement or floor on the ground), [m2] | Afl | 395.4 | 360 |
| 8 | calculated from exterior measurements total windows area, [m2] | Atw | 290.7 | 254.9 |
| 9 | number of stores, [pc.] | NOs | 4.3 | 4 |
| 10 | number of residential flats, premises [pc.] | NOp | 32.4 | 29 |
| 11 | number of living persons per building [Nb] | NOpb | 73.9 | 64 |
| 12 | shape coefficient of buildings (the ratio surface to volume), [m2∙m−3], [m−1] | S/Ve | 0.46 | 0.42 |
| 13 | calculated thermal transmittance of walls components, [W∙m−2·K−1] | Uw | 1.1 | 1.16 |
| 14 | calculated thermal transmittance of peak walls components, [W∙m−2·K−1] | Upw | 1.0 | 0.94 |
| 15 | calculated thermal transmittance of roof projections components, [W∙m−2·K−1] | Ur | 1.25 | 0.72 |
| 16 | calculated thermal transmittance of floor components on the ground, [W∙m−2·K−1] | Ug | 1.61 | 1.41 |
| 17 | calculated thermal transmittance of floors components (floor over basement), [W∙m−2·K−1] | Uf | 1.17 | 1.1 |
| 18 | thermal transmittance of windows (commercial data), [W∙m−2·K−1] | Uwin | 1.88 | 1.6 |
| 19 | calculated heating consumed power, [kW] | Φh | 189.9 | 168.8 |
| 20 | measured, annual energy consumption for heating, [GJ∙year−1] | Qh | 1524.4 | 1316.9 |
| 21 | measured, annual energy consumption for hot water provision, [GJ∙year−1] | Qw,w | 364.1 | 276.47 |
| 22 | measured, the annual heat consumption for building heating converted to the conditions of the standard heating season + energy for hot water provision, [GJ∙year−1] | Qr,h+w,w | 1824.1 | 1710.5 |
| 23 | index of final energy demand for heating and domestic hot water preparation before modernization, [kWh∙m−2·year−1] | FE0 | 253.54 | 222.41 |
| 24 | index of final energy demand for heating and domestic hot water preparation after modernization, [kWh∙m−2·year−1] | FE1 | 143.6 | 121.6 |
| Set: | Parameter: | Standard [13,39,40] |
|---|---|---|
| I | Qh—measured, consumed annual energy for heating [GJ∙year−1], Qww—measured, consumed annual energy for hot water provision [GJ∙year−1] | |
| II | Φh—calculated heating consumed power [kW], | ISO 12831-1:2017-08 |
| Qr,h+ww—measured, the annual heat consumption for building heating converted to the conditions of the standard heating season + energy for hot water provision [GJ∙year−1] | ||
| III | Ve—calculated from exterior measurements the heated volume of building [m3], | ISO 12831-1:2017-08 |
| Af—calculated surface of heated floors from interior measurements [m2] | ISO 12831-1:2017-08 | |
| Aw—calculated from exterior measurements total walls’ surface (net) area [m2] | ISO 9836:1997 | |
| Ar—calculated from exterior measurements surface of roof projection area (net) [m2] | ISO 12831-1:2017-08 | |
| Atw—calculated from exterior measurements total windows area [m2] | ISO 12831-1:2017-08 | |
| Ain—calculated from interior measurements total (net internal area) [m2] | ISO 12831-1:2017-08 | |
| Nopb—number of living persons per building [Nb] | ||
| Nop—number of residential flats, premises [pcs.] | ||
| S/Ve—shape coefficient of buildings (the ratio surface to volume) [m2∙m−3], [m−1] | ISO 9836:1997 | |
| IV | Uw—calculated thermal transmittance of walls components [W∙m−2·K−1] | ISO 6946:2017-10 |
| Upw—calculated thermal transmittance of peak walls components [W∙m−2·K−1] | ISO 6946:2017-10 | |
| Ur—calculated thermal transmittance of roof projections components [W∙m−2·K−1] | ISO 6946:2017-10 | |
| Uf—calculated thermal transmittance of floors components (floor over basement) [W∙m−2·K−1] | ISO 6946:2017-10 | |
| Uwin—thermal transmittance of windows (commercial data) [W∙m−2·K−1] | ISO 6946:2017-10 | |
| Ug—calculated thermal transmittance of floor components on the ground [W∙m−2·K−1] | ISO 6946:2017-10 | |
| Ve—calculated from exterior measurements the heated volume of building [m3] | ISO 9836:1997 | |
| S/Ve—shape coefficient of buildings (the ratio surface to volume) [m2∙m−3], [m−1] | ISO 9836:1997 | |
| Af—calculated surface of heated floors from interior measurements [m2] | ISO 12831-1:2017-08 | |
| Aw—calculated from exterior measurements total walls’ surface (net) area [m2] | ISO 9836:1997 | |
| Ar—calculated from exterior measurements surface of roof projection area (net) [m2] | ISO 12831-1:2017-08 | |
| Atw—calculated from exterior measurements total windows area [m2] | ISO 12831-1:2017-08 | |
| Ain—calculated from interior measurements total (net internal area) [m2] | ISO 12831-1:2017-08 | |
| Nopb—number of living persons per building [Nb] | ||
| Nop—number of residential flats, premises [pc.] | ||
| V | Uw—calculated thermal transmittance of walls components [W∙m−2·K−1] | ISO 6946:2017-10 |
| Upw—calculated thermal transmittance of peak walls components [W∙m−2·K−1] | ISO 6946:2017-10 | |
| Ur—calculated thermal transmittance of roof projections components [W∙m−2·K−1] | ISO 6946:2017-10 | |
| Uf—calculated thermal transmittance of floors components (floor over basement) [W∙m−2·K−1] | ISO 6946:2017-10 | |
| Uwin—thermal transmittance of windows (commercial data) [W∙m−2·K−1] | ISO 6946:2017-10 | |
| Ug—calculated thermal transmittance of floor components on the ground [W∙m−2·K−1] | ISO 6946:2017-10 | |
| Af—calculated surface of heated floors from interior measurements [m2] | ISO 12831-1:2017-08 | |
| Aw—calculated from exterior measurements total walls’ surface (net) area [m2] | ISO 9836:1997 | |
| Ar—calculated from exterior measurements surface of roof projection area (net) [m2] | ISO 12831-1:2017-08 | |
| Atw—calculated from exterior measurements total windows area [m2] | ISO 12831-1:2017-08 | |
| Sets of variables (before thermomodernization) (Recorded in the form of 0–1 information whether the peak wall, external wall, floors, ground floors, windows and flat roof to be thermomodernized). | ||
| Index | Set | Method Estimating | |||||
|---|---|---|---|---|---|---|---|
| ANN | CART | CHAID | MARS | SRT | SV | ||
| MBE [%] | I | 12.9 | 8.7 | 8.7 | 14.3 | 9.9 | 8.6 |
| II | 9.5 | 8.7 | 8.7 | 8.7 | 5.6 | 7.9 | |
| III | 8.8 | 8.7 | 8.7 | 18.4 | 12.2 | 14.0 | |
| IV | 4.0 | 9.5 | 4.0 | 4.0 | 4.7 | 2.8 | |
| V | 4.0 | 9.5 | 4.0 | 6.0 | 6.0 | 1.7 | |
| CV RMSE [%] | I | 23.8 | 28.1 | 28.1 | 29.7 | 27.5 | 26.1 |
| II | 23.8 | 28.1 | 28.1 | 33.9 | 25.7 | 26.8 | |
| III | 20.5 | 28.1 | 28.1 | 37.4 | 27.0 | 39.4 | |
| IV | 13.7 | 20.7 | 24.6 | 14.8 | 13.9 | 28.4 | |
| V | 13.7 | 20.7 | 24.6 | 17.8 | 16.4 | 20.7 | |
| R2 | I | 0.6 | 0.3 | 0.3 | 0.4 | 0.4 | 0.4 |
| II | 0.6 | 0.3 | 0.3 | 0.3 | 0.4 | 0.3 | |
| III | 0.7 | 0.3 | 0.3 | 0.3 | 0.4 | 0.1 | |
| IV | 0.8 | 0.7 | 0.4 | 0.8 | 0.8 | 0.3 | |
| V | 0.8 | 0.7 | 0.4 | 0.7 | 0.8 | 0.6 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szul, T.; Nęcka, K.; Mathia, T.G. Neural Methods Comparison for Prediction of Heating Energy Based on Few Hundreds Enhanced Buildings in Four Season’s Climate. Energies 2020, 13, 5453. https://doi.org/10.3390/en13205453
Szul T, Nęcka K, Mathia TG. Neural Methods Comparison for Prediction of Heating Energy Based on Few Hundreds Enhanced Buildings in Four Season’s Climate. Energies. 2020; 13(20):5453. https://doi.org/10.3390/en13205453
Chicago/Turabian StyleSzul, Tomasz, Krzysztof Nęcka, and Thomas G. Mathia. 2020. "Neural Methods Comparison for Prediction of Heating Energy Based on Few Hundreds Enhanced Buildings in Four Season’s Climate" Energies 13, no. 20: 5453. https://doi.org/10.3390/en13205453
APA StyleSzul, T., Nęcka, K., & Mathia, T. G. (2020). Neural Methods Comparison for Prediction of Heating Energy Based on Few Hundreds Enhanced Buildings in Four Season’s Climate. Energies, 13(20), 5453. https://doi.org/10.3390/en13205453