Analysis of Random Forest Modeling Strategies for Multi-Step Wind Speed Forecasting
Abstract
:1. Introduction
- Does RF provide better results as a standalone model or as an error-correction mechanism for a naive model?
- What is the effect of making a multi-step prediction based on a recursive (step-by-step) vs. a direct (single jump) methodology?
- How much training data is required for model performance to show asymptotic behavior (i.e., reach a stable optimum even as more training data is added)?
2. Materials and Methods
2.1. Random Forest Regression
2.2. Testing Sites
2.3. Data Preprocessing
2.4. Testing
3. Results and Discussion
3.1. FINO1
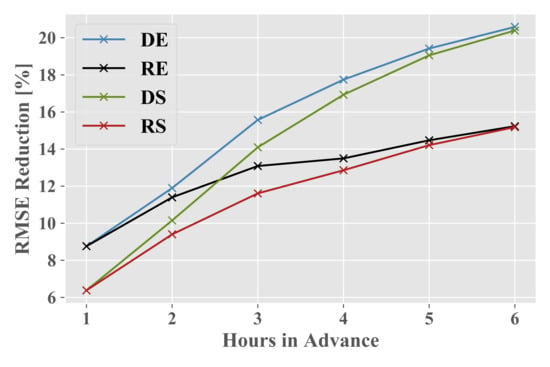
3.1.1. Modeling Strategy Comparison
3.1.2. Training Data Availability
3.2. SGP C1
3.2.1. Modeling Strategy Comparison
3.2.2. Training Data Availability
4. Conclusions
- Quantification of the effect of endogenous models vs. models which utilize exogenous variables
- Which exogenous variables are most beneficial for multi-step wind speed forecasting
- Which ML models, when used both individually and within an ensemble framework, are best suited for wind speed forecasting
- Whether the optimal ML modeling methodology changes with the forecasting timescale (e.g., are certain models and modeling strategies better suited for very short-term forecasting while others are better suited for medium/long term forecasting?)
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ML | Machine learning |
| ARM | Atmospheric Radiation Measurement |
| SGP | Southern Great Plains |
| SGP C1 | Southern Great Plains central facility site |
| NWP | Numerical Weather Prediction |
| RF | Random forest |
| MSE | Mean squared error |
| MSL | Above mean sea level |
| THWAPS | Temperature, humidity, wind, and pressure sensors |
| RS | Recursive standalone RF model |
| RE | Recursive RF model predicting persistence modeling error |
| DS | Direct standalone RF model |
| DE | Direct RF model predicting persistence modeling error |
| RMSE | Root mean squared error |
| IAV | Inter-annual variability |
| LLJ | Low-level jet |
| Probability density function |
Appendix A. Data Availability
| Samples | ||||
|---|---|---|---|---|
| FINO1 | SGP C1 | |||
| Hours in Advance | Training | Testing | Training | Testing |
| 1 | 60,984 | 6777 | 73,012 | 8113 |
| 2 | 59,402 | 6601 | 65,280 | 7254 |
| 3 | 58,918 | 6547 | 63,046 | 7006 |
| 4 | 58,536 | 6505 | 62,427 | 6937 |
| 5 | 58,203 | 6468 | 61,996 | 6889 |
| 6 | 57,904 | 6434 | 61,635 | 6849 |

Appendix B. Testing Results
| FINO1 | ||||||
|---|---|---|---|---|---|---|
| Hours in Advance | ||||||
| Model | 1 | 2 | 3 | 4 | 5 | 6 |
| Persistence | 0.853 | 1.279 | 1.592 | 1.839 | 2.065 | 2.247 |
| DE | 0.822 | 1.222 | 1.506 | 1.735 | 1.932 | 2.094 |
| RE | 0.822 | 1.224 | 1.511 | 1.743 | 1.946 | 2.111 |
| DS | 0.838 | 1.246 | 1.533 | 1.765 | 1.964 | 2.127 |
| RS | 0.838 | 1.244 | 1.533 | 1.768 | 1.970 | 2.137 |
| SGP C1 | ||||||
| Hours in Advance | ||||||
| Model | 1 | 2 | 3 | 4 | 5 | 6 |
| Persistence | 0.799 | 1.202 | 1.490 | 1.719 | 1.900 | 2.055 |
| DE | 0.729 | 1.059 | 1.258 | 1.414 | 1.531 | 1.632 |
| RE | 0.729 | 1.065 | 1.295 | 1.487 | 1.625 | 1.742 |
| DS | 0.748 | 1.080 | 1.280 | 1.428 | 1.538 | 1.636 |
| RS | 0.748 | 1.089 | 1.317 | 1.498 | 1.630 | 1.743 |
| FINO1 | |||||||
|---|---|---|---|---|---|---|---|
| Years of Data | |||||||
| Hours in Advance | 1 | 2 | 3 | 4 | 5 | 6 | All |
| 1 | 0.848 | 0.837 | 0.831 | 0.824 | 0.824 | 0.822 | 0.822 |
| 2 | 1.262 | 1.249 | 1.238 | 1.224 | 1.224 | 1.222 | 1.222 |
| 3 | 1.555 | 1.541 | 1.521 | 1.506 | 1.504 | 1.506 | 1.506 |
| 4 | 1.782 | 1.773 | 1.747 | 1.740 | 1.734 | 1.736 | 1.735 |
| 5 | 1.982 | 1.969 | 1.949 | 1.944 | 1.930 | 1.933 | 1.932 |
| 6 | 2.153 | 2.133 | 2.117 | 2.109 | 2.091 | 2.097 | 2.094 |
| SGP C1 | |||||||
| Years of Data | |||||||
| Hours in Advance | 1 | 2 | 3 | 4 | 5 | 6 | All |
| 1 | 0.749 | 0.742 | 0.739 | 0.735 | 0.734 | 0.733 | 0.729 |
| 2 | 1.096 | 1.083 | 1.076 | 1.072 | 1.067 | 1.064 | 1.059 |
| 3 | 1.311 | 1.292 | 1.285 | 1.277 | 1.268 | 1.265 | 1.258 |
| 4 | 1.478 | 1.453 | 1.442 | 1.434 | 1.423 | 1.420 | 1.414 |
| 5 | 1.601 | 1.574 | 1.560 | 1.549 | 1.537 | 1.535 | 1.531 |
| 6 | 1.703 | 1.676 | 1.663 | 1.650 | 1.640 | 1.636 | 1.632 |
References
- Feng, J. Artificial Intelligence for Wind Energy (AI4Wind): A State of the Art Report; Technical Report; Technical University of Denmark, Department of Wind Energy: Lyngby, Denmark, 2019. [Google Scholar]
- Dupré, A.; Drobinski, P.; Alonzo, B.; Badosa, J.; Briard, C.; Plougonven, R. Sub-hourly forecasting of wind speed and wind Energy. Renew. Energy 2020, 145, 2373–2379. [Google Scholar] [CrossRef]
- Soman, S.S.; Zareipour, H.; Malik, O.; Mandal, P. A review of wind power and wind speed forecasting methods with different time horizons. In Proceedings of the North American Power Symposium 2010, Arlington, TX, USA, 26–28 September 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–8. [Google Scholar]
- Lahouar, A.; Slama, J.B.H. Hour-ahead wind power forecast based on random forests. Renew. Energy 2017, 109, 529–541. [Google Scholar] [CrossRef]
- Feng, C.; Cui, M.; Hodge, B.M.; Zhang, J. A data-driven multi-model methodology with deep feature selection for short-term wind forecasting. Appl. Energy 2017, 190, 1245–1257. [Google Scholar] [CrossRef] [Green Version]
- Niu, D.; Pu, D.; Dai, S. Ultra-short-term wind-power forecasting based on the weighted random forest optimized by the niche immune lion algorithm. Energies 2018, 11, 1098. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.; Sun, H.; Zhang, J. Multistep wind speed and wind power prediction based on a predictive deep belief network and an optimized random forest. Math. Probl. Eng. 2018, 2018. [Google Scholar] [CrossRef] [Green Version]
- Shi, K.; Qiao, Y.; Zhao, W.; Wang, Q.; Liu, M.; Lu, Z. An improved random forest model of short-term wind-power forecasting to enhance accuracy, efficiency, and robustness. Wind. Energy 2018, 21, 1383–1394. [Google Scholar] [CrossRef]
- Vassallo, D.; Krishnamurthy, R.; Fernando, H.J.S. Utilizing Physics-Based Input Features within a Machine Learning Model to Predict Wind Speed Forecasting Error. Wind. Energy Sci. Discuss. 2020, 1–18. [Google Scholar] [CrossRef]
- Haupt, S.E.; Mahoney, W.P.; Parks, K. Wind power forecasting. In Weather Matters for Energy; Springer: Berlin/Heidelberg, Germany, 2014; pp. 295–318. [Google Scholar]
- Wang, J.; Song, Y.; Liu, F.; Hou, R. Analysis and application of forecasting models in wind power integration: A review of multi-step-ahead wind speed forecasting models. Renew. Sustain. Energy Rev. 2016, 60, 960–981. [Google Scholar] [CrossRef]
- Ahmed, A.; Khalid, M. An intelligent framework for short-term multi-step wind speed forecasting based on Functional Networks. Appl. Energy 2018, 225, 902–911. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Loh, W.Y. Classification and regression tree methods. Wiley Statsref. Stat. Ref. Online 2014. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- Neumann, T.; Nolopp, K. Three years operation of far offshore measurements at FINO1. DEWI Mag. 2007, 30, 42–46. [Google Scholar]
- Westerhellweg, A.; Neumann, T.; Riedel, V. Fino1 mast correction. Dewi Mag. 2012, 40, 60–66. [Google Scholar]
- Sisterson, D.; Peppler, R.; Cress, T.; Lamb, P.; Turner, D. The ARM southern great plains (SGP) site. Meteorol. Monogr. 2016, 57, 6.1–6.14. [Google Scholar] [CrossRef]
- Atmospheric Radiation Measurement (ARM) user facility. Temperature, Humidity, Wind, and Pressure Sensors (THWAPS). In 2003-01-01 to 2014-12-31, Southern Great Plains (SGP) Central Facility, Lamont, OK (C1); Kyrouac, J., Ermold, B., Eds.; ARM Data Center: Cambridge, UK, 1999. [Google Scholar] [CrossRef]
- Ritsche, M. Temperature, Humidity, Wind and Pressure Sensors (THWAPS) Handbook; Technical report; DOE Office of Science Atmospheric Radiation Measurement (ARM) Program: Cambridge, UK, 2011. [Google Scholar]
- Chatfield, C.; Prothero, D. Box-Jenkins seasonal forecasting: Problems in a case-study. J. R. Stat. Soc. Ser. 1973, 136, 295–315. [Google Scholar] [CrossRef]
- Dickey, D.A.; Pantula, S.G. Determining the order of differencing in autoregressive processes. J. Bus. Econ. Stat. 1987, 5, 455–461. [Google Scholar]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2018. [Google Scholar]
- Bontempi, G.; Taieb, S.B.; Le Borgne, Y.A. Machine learning strategies for time series forecasting. In European Business Intelligence Summer School; Springer: Berlin, Heidelberg, Germany, 2012; pp. 62–77. [Google Scholar]
- Pryor, S.C.; Shepherd, T.J.; Barthelmie, R.J. Interannual variability of wind climates and wind turbine annual energy production. Wind. Energy Sci. 2018, 3, 651. [Google Scholar] [CrossRef] [Green Version]
- Brower, M. Wind Resource Assessment: A Practical Guide to Developing a Wind Project; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- McGaughey, G.; Walters, W.P.; Goldman, B. Understanding covariate shift in model performance. F1000Research 2016, 5, 6. [Google Scholar] [CrossRef]
- Fruehmann, R.K.; Neumann, T. Wake effects at FINO 1–new observations since the construction of Trianel Borkum & Borkum Riffgrund I wind farms. In Proceedings of the WindEurope Summit 2016, Hamburg, Germany, 27–30 September 2016; EWEA: Brussels, Belgium, 2016. [Google Scholar]
- Westerhellweg, A.; Cañadillas, B.; Kinder, F.; Neumann, T. Wake measurements at Alpha Ventus–dependency on stability and turbulence intensity. J. Phys. Conf. Ser. Iop Publ. 2014, 555, 012106. [Google Scholar] [CrossRef] [Green Version]
- Taieb, S.B.; Bontempi, G.; Atiya, A.F.; Sorjamaa, A. A review and comparison of strategies for multi-step ahead time series forecasting based on the NN5 forecasting competition. Expert Syst. Appl. 2012, 39, 7067–7083. [Google Scholar] [CrossRef] [Green Version]
- Whiteman, C.D.; Bian, X.; Zhong, S. Low-level jet climatology from enhanced rawinsonde observations at a site in the southern Great Plains. J. Appl. Meteorol. 1997, 36, 1363–1376. [Google Scholar] [CrossRef]
- Song, J.; Liao, K.; Coulter, R.L.; Lesht, B.M. Climatology of the low-level jet at the southern Great Plains atmospheric boundary layer experiments site. J. Appl. Meteorol. 2005, 44, 1593–1606. [Google Scholar] [CrossRef]
- Wimhurst, J.J.; Greene, J.S. Oklahoma’s future wind energy resources and their relationship with the Central Plains low-level jet. Renew. Sustain. Energy Rev. 2019, 115, 109374. [Google Scholar] [CrossRef]
- Berg, L.K.; Riihimaki, L.D.; Qian, Y.; Yan, H.; Huang, M. The low-level jet over the southern Great Plains determined from observations and reanalyses and its impact on moisture transport. J. Clim. 2015, 28, 6682–6706. [Google Scholar] [CrossRef]
- Opitz, D.; Maclin, R. Popular ensemble methods: An empirical study. J. Artif. Intell. Res. 1999, 11, 169–198. [Google Scholar] [CrossRef]
- Bokde, N.; Feijóo, A.; Villanueva, D.; Kulat, K. A review on hybrid empirical mode decomposition models for wind speed and wind power prediction. Energies 2019, 12, 254. [Google Scholar] [CrossRef] [Green Version]









| FINO1 | |||||
|---|---|---|---|---|---|
| [m s] | [C] | ||||
| Mean | 8.99 | 0.09 | −0.22 | −0.28 | 11.31 |
| St. Dev. | 4.37 | 0.05 | 0.63 | 0.69 | 5.81 |
| Max | 31.48 | 0.50 | 1.00 | 1.00 | 41.92 |
| Min | 0.24 | 0.00 | −1.00 | −1.00 | −6.67 |
| SGP C1 | |||||
| [m s] | [C] | ||||
| Mean | 6.20 | 0.19 | −0.23 | 0.13 | 19.79 |
| St. Dev. | 2.95 | 0.14 | 0.78 | 0.57 | 8.39 |
| Max | 20.34 | 0.98 | 1.00 | 1.00 | 44.17 |
| Min | 0.24 | 0.00 | −1.00 | −1.00 | −8.11 |
Sample Availability: Samples of the data and code may be found at https://github.com/dvassall/WS_Forecasting_Strategies_Sample. | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vassallo, D.; Krishnamurthy, R.; Sherman, T.; Fernando, H.J.S. Analysis of Random Forest Modeling Strategies for Multi-Step Wind Speed Forecasting. Energies 2020, 13, 5488. https://doi.org/10.3390/en13205488
Vassallo D, Krishnamurthy R, Sherman T, Fernando HJS. Analysis of Random Forest Modeling Strategies for Multi-Step Wind Speed Forecasting. Energies. 2020; 13(20):5488. https://doi.org/10.3390/en13205488
Chicago/Turabian StyleVassallo, Daniel, Raghavendra Krishnamurthy, Thomas Sherman, and Harindra J. S. Fernando. 2020. "Analysis of Random Forest Modeling Strategies for Multi-Step Wind Speed Forecasting" Energies 13, no. 20: 5488. https://doi.org/10.3390/en13205488
APA StyleVassallo, D., Krishnamurthy, R., Sherman, T., & Fernando, H. J. S. (2020). Analysis of Random Forest Modeling Strategies for Multi-Step Wind Speed Forecasting. Energies, 13(20), 5488. https://doi.org/10.3390/en13205488