Cellulose Ester Insulation of Power Transformers: Researching the Influence of Moisture on the Phase Shift Angle and Admittance

Abstract

This study investigates the frequency–temperature relations between the phase angle φ and admittance Y for composites of cellulose, synthetic ester, and water nanoparticles. We determined the activation energy value for the relaxation time of a phase shift angle ΔW_φ ≈ (0.783 ± 0.0744) eV, which was related to the shift of φ(f) waveforms in higher frequency area with increasing temperature. We found that the position of admittance frequency waveforms in double logarithmic coordinates was simultaneously influenced by the temperature dependence of admittance and its relaxation time. Activation energy values for the relaxation time of admittance ΔW_τ ≈ (0.796 ± 0.0139) eV and the activation energy value of admittance ∆W_Y ≈ (0.800 ± 0.0162) eV were determined. It was found that all three activation energy values were identical and their average was ΔW ≈ (0.793 ± 0.0453) eV. Impregnation with synthetic ester resulted in a decrease of activation energy by 0.26 eV compared to the impregnation with insulating oil. This was related to higher dielectric permittivity of the synthetic ester.

1. Introduction

Power transformers use the so-called liquid–solid insulation. The solid component is cellulose materials, i.e., paper and electrotechnical pressboards. The most commonly used insulating fluids found in power transformers is mineral oil [1]. Its versatility, high availability, and positive electrical insulating properties show that mineral oil can be used as a basic insulating liquid for many years.

Alternative fluids (i.e., natural and synthetic ester oils) are required to mitigate the impact of insulation materials on the natural environment. Compared to mineral oils, these types of liquids have a high biodegradability of 97% for natural esters and over 89% for synthetic esters [2]. Ester oils are classified as non-toxic (natural esters) and low-toxic (synthetic esters) [3]. Compared to mineral oil, synthetic esters are characterized by a significantly higher flash point and fire point [4,5,6].

In order to enable long, failure-free operation of a transformer, the insulating liquid must have high oxidative stability. Compared to mineral oil, low oxidation resistance is the main disadvantage of natural ester oils. Synthetic ester oils show markedly higher oxidation stability compared to mineral oils [7]. An important aspect is the ability of an insulating liquid to dissolve water molecules [8]. The higher it is, the more water molecules become trapped in the insulating liquid, thus preventing them from reaching the solid cellulose insulation. The solubility of water in the insulating liquid is closely related to temperature and increases exponentially as it increases [9].

An analysis [3] of the approximate maximum amount of water dissolved in the insulating fluid at 23 °C indicates that mineral oil (55 ppm) and silicone oil (220 ppm) are characterized by the lowest ability of water accumulation, which is contrary to natural esters (1100 ppm) and synthetic esters (2600 ppm). Prior research has shown that an increase in moisture causes an acceleration of cellulose degradation [3].

Moisture deteriorates the parameters of the liquid–solid insulation in power transformers, as moisture penetrates from the outside. During precipitation, the upper part of the transformer and air below cools down. This reduces the pressure of the air inside the transformer compared to the air outside. Under the influence of the pressure difference, moisture enters the transformer through capillaries in the seals. The water is then transported by oil into the cellulose and is absorbed by it. It is related to the fact that water solubility in cellulose is over a thousand times higher than in transformer oil [10]. During many years of exploitation, the moisture content in cellulose composites and mineral oil gradually increases from the initial level of about 0.8% to over 5% by weight, lowering the quality of paper-oil insulation and power transformer reliability.

The methods determining the moisture content level in the solid component that insulates the power transformer are non-destructive electrical methods, which include measurement methods in the frequency domain (i.e., frequency domain spectroscopy (FDS) [11,12,13]) and measurements in the time domain with the use of DC voltage (i.e., the return voltage measurement (RVM) method [14,15] and the polarization depolarization current (PDC) method [16,17]). Generally, analyzing dielectric relaxation processes in the time and frequency domains have been based on a number of models, each of which has a reliable physical justification [18,19,20,21].

In [22], on the basis of an experimental results analysis, it was found that the dependence of DC conductivity on moisture content was much stronger than linear. DC conductivity took place through a quantum effect of electron tunneling between potential wells produced by water molecules.

In [23,24,25,26,27], the quantum mechanical phenomenon of electron tunneling between potential wells produced by water nanoparticles was used to analyze the dependence of AC conductivity, dielectric permittivity, and the loss tangent of cellulose composites, insulating oil and water nanoparticles on temperature, frequency, and moisture content. The results obtained during the analysis made it possible to develop methods that converted the above-mentioned parameters obtained at any temperature that ranged from 10–80 °C.

The mechanisms that increase moisture in the cellulose insulation of energy transformers contains mineral oil or synthetic esters, i.e., water precipitate during cellulose degradation and its penetration from the outside and cellulose supply. In [23,26,28], the DC and AC conductivity for damp pressboards impregnated with insulating oil was investigated. It was found that the conductivity was carried out via electron tunneling between water droplets placed in cellulose fibers. The average dimensions of the nanodrop were about 2.24 nm. On average, the nanodrop consisted of about 200 water molecules. The synthetic ester used in this work was, in many respects, similar to insulating oil. In ester, as well as in oil, the content of dissolved water is much lower than in cellulose. The way samples were prepared was identical to the way samples impregnated with insulating oil were made. In [29,30], processes of electrotechnical pressboard oil impregnation, in particular oil impregnation speed, are discussed. This means the electrotechnical pressboard was impregnated with synthetic ester, while water also occurred in cellulose fibers as nanodrops. Thus, damp cellulose impregnated with synthetic esters should be treated as cellulose composites, synthetic esters, and water nanoparticles.

It follows that the same test methods should be used to determine the moisture content in the liquid–solid insulation of hermetic energy transformers filled with synthetic esters, i.e., transformers filled with mineral oil. Since the electrical properties of the synthetic ester differed from those of the mineral oil, a laboratory test of cellulose composites, synthetic esters, and water nanoparticles should be conducted.

The basic parameters determined using the FDS method are the phase shift angle and the admittance. On their basis, the capacity and resistance of the insulation and material parameters, as well as their conductivity and permeability, are calculated. The phase shift angle and the admittance significantly depend on insulation temperature. The temperature dependencies are described via activation energy. Two activation energies must be distinguished. The activation energy for relaxation time causes curves to shift into higher frequency areas, such as when the temperature increases. On the other hand, such a parameter as admittance also has a second activation energy, which causes the curves to shift along the vertical axis as the temperature increases. The temperature dependence of admittance is simultaneously influenced by the two above-mentioned activation energies. As the temperature increases, the activation energy of relaxation time causes frequency dependence to shift along the frequency axis. On the other hand, activation energy of admittance causes curves to shift along the vertical axis with increasing temperature. Thus far, the literature on the subject does not disclose any papers examining the influence of temperature on frequency dependencies for the phase shift angle and the admittance of damp electrotechnical pressboards impregnated with synthetic esters.

A sample pressboard with 5% water content was selected for measurements. Reaching or exceeding this moisture content may result in catastrophic failure of the power transformer.

2. Materials and Methods

This research used a brand new synthetic ester, MIDEL 7131. A sample of Weidman’s 1 mm thick electrotechnical pressboard, designed for the construction of power transformers, was dried in a vacuum at 353.15 K for two days. After drying the sample, its mass was determined and obtained using the sample after being moistened. Then, its preset value was calculated. Moreover, it was moistened in atmospheric air until it reached a moisture content of 5%. After reaching the set moisture level, the sample was immersed in the MIDEL 7131 synthetic ester. For impregnation, we used a factory new ester dedicated to power transformers with a moisture content of 50 ppm. In order to establish thermodynamic balance between the pressboard, synthetic esters, and moisture, the sample was seasoned in the ester in a hermetic container for over 6 months at room temperature. This was confirmed by [30]. The atmospheric pressure impregnation process established the thermodynamic equilibrium between cellulose, oil, and moisture, and it should be carried for over 6 months.

A three-electrode measuring system was used, the diagram of which is shown in Figure 1. In the measuring capacitor between electrodes, we used a sample of moistened pressboard impregnated with synthetic ester. The three-electrode measuring system combined with the sample was placed in a hermetic vessel and flooded with a small amount of ester. The whole system was placed in a climatic chamber with temperature maintenance accuracy of ±0.1 K. The system took about 5 h to reach the set temperature. Such a long time was related to the high weight of the system (about 12 kg). After reaching the set temperature, the climate chamber maintained the temperature for many hours. The uncertainty of maintaining the temperature over a long period of time was ±0.1 K. The temperature of the measuring capacitor was controlled using the PT 1000 sensor and the Agilent meter. The tests were carried out using an Omikron FDS Dirana type meter. A Dirana meter has a measuring frequency range of 0.0001 Hz to 5000 Hz. The test determined the impedance frequency dependence and the pressboard’s phase shift angle when impregnated with synthetic esters at measurement temperatures of 253.15 K, 273.15 K, 283.15 K, 293.15 K, 303.15 K, 314.15 K, and 323.15 K.

Based on the measured values of admittance Y and φ, the FDS meter used its own software to calculate parameters such as conductance (G_p), capacitance (C_p), loss (ε”), and loss angle tangent (tan δ) used in the analysis of the transformer insulation condition. On the basis of the conductance G_p and the capacitance C_p, using the geometrical dimensions of the dielectric material, such as thickness d and voltage electrode surface area S, it is possible to calculate material parameters, conductivity σ, and the relative dielectric permittivity ε of the tested material.

Conductance (G_p), capacitance (C_p), loss (ε”), loss angle tangent (tan δ), conductivity (σ), and dielectric permittivity (ε) are complex functions of the admittance and phase shift angle. The geometrical dimensions of the material are also included in the conductivity and permittivity formulas.

Therefore, we performed an analysis of the basic AC parameters for cellulose composites, i.e., synthetic esters, water nanoparticles, admittance, and phase shift angle.

3. Results and Discussion

3.1. Effect of Temperature on the Phase Angle Values

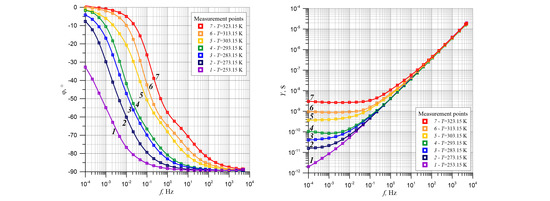
Figure 2 shows the frequency dependence of the phase shift angle of the cellulose composite, synthetic ester, and water nanoparticles measured at measurement temperatures of 253.15 K, 273.15 K, 283.15 K, 293.15 K, 303.15 K, 314.15 K, and 323.15 K.

As can be seen from the picture, measuring points were relatively rarely located, i.e., three per decade. This was because the need to perform time-consuming measurements in the ultra-low frequency area. Indeed, at a measuring frequency of 0.0001 Hz, a single alternating voltage change interval was 10,000 s, i.e., about 2.77 h. In order to perform an accurate analysis of the waveforms shown in Figure 2, the values of the phase shift angles between measuring points were necessary. In order to obtain intermediate values between measuring points, polynomial approximation of experimental courses was performed (Figure 2). The approximation was performed using method proposed in a previous study [27]. The use of polynomial approximation is often associated with the appearance of oscillations between the approximation nodes at the end of an approximation range. To avoid their manifestation, the measurement data was extrapolated using a linear function below and above the range of measurement points. The use of measurement data extrapolation made it possible to shift approximation oscillations into a range of added extrapolation points. Thanks to this procedure, oscillations did not occur in the range of measurement data, thus enabling precise data analysis.

The results of the approximation are presented in Figure 2 in the form of continuous lines. Each of these lines consists of 200 points per decade, which was obtained by approximation. The following two arguments prove the high quality of approximation. First, values of determination coefficients R² were presented in

Table 1. Values of the coefficient of determination R² for approximations of the phase shift angle and admittance.

	253.15 K	273.15 K	283.15 K	293.15 K	303.15 K	313.15 K	323.15 K
φ, °	0.999996	0.999998	0.999997	0.999997	0.999998	0.999998	0.999998
Y, S	0.99999988	0.99999999	0.99999997	0.99999995	0.99840959	0.99663465	0.99601914

. As Table 1 shows, the values of determination coefficients R² for runs, obtained for all measurement temperatures, were close to unity. The lowest value, obtained for the measurement temperature T = 303 K, was R² = 0.999996, proving a very high quality of polynomial approximation performed with a method proposed in a previous paper [27].

The second argument is the differences between experimental values and approximation results, expressed in percent and shown in Figure 3. The figure shows that the biggest differences are observed in the range of lowest frequencies and highest temperatures, as well as that their values do not exceed 1.5%. This is a highly satisfactory result.

Figure 2 shows that the phase shift angle for the lowest measurement frequency 10⁻⁴ Hz was close to zero. This means that conductivity at low frequencies for these temperatures (i.e. 283.15 K, 293.15 K, 303.15 K, 314.15 K and 323.15 K) is mostly resistive. Only when the measurement temperature was 253.15 K did the phase shift angle at 10⁻⁴ Hz become greater than -32°. In this case, there was also the capacitive component of the complex conductivity.

As the frequency increases, especially at temperatures of 283.15 K and above, the module value of the phase shift angle increased more rapidly. At a certain frequency, the value depends on the measuring temperature. This process can undergo certain refraction; for example, for measuring a temperature of 323.15 K at a frequency of about 0.3 Hz. At this point, the curve clearly changed its slope and slowly began moving to a value of −90°, which is characteristic of this type of capacitive conductivity. In order to show such a trend, the values of dφ(f)/d(logf) were calculated on the basis of approximations of dφ(f)/d(logf) derivatives, which are shown in Figure 4.

We analyze the waveforms of the derivative dφ(f)/d(logf), shown in Figure 4, using the example of a waveform at a measurement temperature of 323.15 K. The first derivation of the function allowed us to determine the places of fastest change for the function. For the decreasing function, which was the dependence of the phase shift angle on the frequency, it was the minimum position. At this point, the rate of change of the angle of the phase shift was obtained by the maximum value. For the point with the slowest function change, there was a maximum value of the derivative. Figure 4 shows that the frequency dependence of the phase angle of shift was based on two distinct minima at frequencies of about 0.1 Hz and 10 Hz. They were separated from each other by a clear maximum, which was about 2 Hz. Changes in the phase angle with frequency took place in two stages. The low-frequency stage was characterized by a faster phase shift angle change than the high-frequency stage 2. This was due to the fact that the depth of the first minimum was more than twice as fast than the second minimum. The waveforms obtained for the remaining measurement temperatures showed two minima and one maximum separating them, the positions of which moved into the area of lower frequencies with a temperature decrease. The lower the temperature, the less the minimum was visible at a higher frequency. As shown in the Figure 2, at 253.15 K the downward path differs significantly from the other temperatures. On this waveform (Figure 4, curve 1), in the low frequency region, there are two closely spaced minima of almost equal values with much smaller depths compared to the minima for temperatures of 273.15 K and above. In our opinion, at this temperature the water was solid, which changed the electrical parameters of ice compared to liquid water. During the transition from liquid to solid, the dielectric permittivity and conductivity of water decreased. This undoubtedly impacted the phase shift angle, which can be seen in the phase shift angle (Figure 2) and its derivative of the frequency logarithm (Figure 4). After water transitioned to liquid at 253.15 K, the phase shift angle curves and its derivative significantly differed from water in a liquid state. We did not consider the curves obtained at 253.15 K.

Slope change in the frequency range of 0.3 Hz is clearly visible in Figure 5, where the dependence of the phase shift angle module, measured at the temperature 323.15 K, on the frequency in double logarithmic coordinates is shown. For the frequencies below 0.3 Hz, the smallest squares of the course is given by the following formula:

$$\log \phi =874.4\times f^{0.58}$$

(1)

The factor R² = 0.9855 indicates high quality approximation. The second part, above 0.3 Hz, is described by the formula:

$$\log \phi =92.3\times f^{0.135}$$

(2)

The R² coefficient in this case is 0.9638. Similar results were obtained for the remaining measurement temperatures.

The refraction and slowing down of φ(f) in the higher frequency areas, as shown in Figure 2, Figure 4, and Figure 5, indicate that there are two mechanisms of dielectric relaxation in cellulose composites: synthetic ester and water nanoparticles. The first is characteristic for low and ultra-low frequency areas. The second is found in higher frequency areas.

An increase in temperature causes a shift in high frequency areas (Figure 2). This is related to a decrease in activation energy for the relaxation time of the phase shift angle [31,32]:

$${\tau }_{\phi }(T)={\tau }_0\exp \left(\frac{\Delta W_{\phi }}{kT}\right),$$

(3)

where ΔW_φ is the activation energy for the relaxation time of the phase shift angle and τ₀ is the numerical factor.

The FDS meter does not directly measure relaxation times. On the basis of FDS testing, the value of the relaxation time can be determined with the numerical factor τ₀ by analyzing the phase shift angle after temperatures rise into higher frequency areas (Figure 2). For this purpose, we selected a specific value of the phase shift angle and read the frequencies, at which this value occurred at different temperatures. The relaxation time value, to the nearest unspecified constant value, was identical for all temperatures (see Formula (4)) and determined by the following formula:

$${\tau }_i\left(T,{\phi }_i\right)=\frac{\tau (T)}{{\tau }_0}=\frac{1}{2\cdot \pi \cdot f\left(T,{\phi }_i\right)},$$

(4)

where τ(T) is actual relaxation time, φ_i is the selected value of the phase shift angle, τ₀ is a more or less undefined constant value equal for all temperatures, and f(T, φ_i) is the frequency at which the selected value of the phase shift angle occurs.

In order to precisely determine the activation energy for the relaxation time of the phase shift angle φ(f), 15 values of the phase shift angle from −10° to −80° with a step of 5° were selected. Selecting such a large number of displacement angles allows for the determination of activation energy in a wide frequency range, as well as for high accuracy calculation of mean value and measurement uncertainty. Figure 6 shows Arrhenius’ diagrams for the frequency f(T, φ_i) with 15 selected values of φ_i as a function of inverse 1000/T temperature and the results of their linear approximation using the least squares method. The approximation waveforms are almost parallel for different values of phase shift angles. This means that the corresponding values of activation energy for relaxation times are close to each other. The determination coefficients R² obtained for the approximation waveforms are shown in

Table 2. Activation energy values for relaxation time in the phase shift angle; activation energy values for relaxation time in admittance; and activation energy values for relaxation time in determination factors R².

No.	Activation Energy for Relaxation Time in the Phase Shift Angle			Activation Energy for Relaxation Time in Admittance			Activation Energy in Admittance
	φ, °	ΔWφ, eV	R2, a.u.	Y, S	ΔWτ, eV	R2, a.u.	f, Hz	ΔWY, eV	R2, a.u.
1	−10	0.776	0.988	1.00 × 10−9	0.760	0.988	0.006	0.799	0.992
2	−15	0.761	0.989	1.58 × 10−9	0.773	0.989	0.013	0.809	0.992
3	−20	0.756	0.990	2.51 × 10−9	0.781	0.990	0.026	0.820	0.993
4	−25	0.747	0.990	3.98 × 10−9	0.788	0.990	0.055	0.828	0.994
5	−30	0.742	0.991	6.31 × 10−9	0.795	0.991	0.114	0.826	0.995
6	−35	0.735	0.991	1.00 × 10−8	0.796	0.991	0.238	0.817	0.995
7	−40	0.726	0.990	1.58 × 10−8	0.801	0.990	0.496	0.806	0.995
8	−45	0.720	0.992	2.51 × 10−8	0.803	0.992	1.035	0.797	0.994
9	−50	0.715	0.992	3.98 × 10−8	0.803	0.992	2.159	0.791	0.994
10	−55	0.720	0.991	6.31 × 10−8	0.805	0.991	4.504	0.788	0.994
11	−60	0.754	0.991	1.00 × 10−7	0.806	0.991	9.394	0.785	0.994
12	−65	0.830	0.991	1.58 × 10−7	0.805	0.991	19.595	0.784	0.994
13	−70	0.893	0.991	2.51 × 10−7	0.809	0.991	40.872	0.783	0.994
14	−75	0.926	0.991	3.98 × 10−7	0.806	0.991	85.254	0.782	0.994
15	−80	0.941	0.991	6.31 × 10−7	0.805	0.991	177.828	0.782	0.994
Mean		0.783	0.994		0.796	0.990		0.800	0.994
Standard deviation		0.0744	0.0042		0.0139	0.0009		0.0162	0.0009
ΔW ≈ (0.793 ± 0.0453) eV/R2 ≈ (0.993 ± 0.0031)

. As can be seen, the values of R² range from 0.9499 to 0.9794. These results are close to unity, which indicates a high quality of linear approximation. On the basis of approximation formulae, activation energy values for relaxation times were determined for all values of phase shift angles from −10° to −80°. The activation energy values for relaxation times in the phase shift angle are shown in Table 2 and Figure 7. The mean values of activation energy, determination factors R², and standard deviation were calculated from 15 residual values, as presented in Table 2.

As can be seen from Table 2, the average value of the activation energy for the relaxation time of the phase shift angle is ΔW_φ ≈ (0.783 ± 0.0744) eV. Figure 7 shows that only in the area of the highest values of the phase angle module the activation energy slightly exceeds the mean value plus standard deviation. This may be due to the fact that starting from the value phase shift angle of −70°, the slope of the φ(f) curves decreases (Figure 2). This lowers the accuracy of determining the frequency values at which the phase shift angles selected for the activation energy calculation can occur. These inaccuracies can be seen in Figure 6 for large values of φ.

3.2. Effect of Temperature on the Admittance Value

Figure 8 shows, in the form of cellulose composite admittance values, synthetic ester and water nanoparticles measured at temperatures between 253.15 K to 323.15 K. As can be seen from Figure 8, in the ultra-low frequency area for each temperature, except 253.15 K, the admittance value did not depend on the frequency. In this frequency area, the admittance value only depended on the temperature and not relaxation time. As the frequency increased further, the admittance value increased. As the temperature increased, it moved to a higher frequency area. This was due to the change in relaxation time as temperature increased. The analysis of the experimental results shown in Figure 8 show that the conductance value in the ultra-low frequency area depend on temperature. In the high frequency area, there was an influence of temperature on the relaxation time changes. However, the curve for 253.15 K behaved differently than the others. This may be due to the fact that 253.15 K was 20 K lower than the freezing point. Therefore, in a further analysis of the results, this curve was not considered.

Similar to the phase shift angle value, the experimental results were approximated using the polynomial method and are presented in Figure 8 with continuous lines [27]. The values of determination factor R² for the processes approximated by admittance are presented in Table 1. As can be seen, these values are close to unity. This proves a high approximation quality.

Figure 9 shows the percentage differences between the approximation and experimental results. As shown in Figure 9, these differences in the ultra-low frequency area did not exceed 0.45% and decreased with increasing frequency. This indicates a very high quality of polynomial approximation.

Figure 10 shows the values of d(logY)/d(logf) derivatives, obtained after differentiating the approximation, as shown in Figure 8.

The curve for the temperature 253.15 K differed significantly from others. There was a clear minimum around 8 × 10⁻⁴ Hz. On the remaining runs, only slowdowns were visible. Therefore, similarly to the analysis of the phase shift angle, the curve for the temperature 253.15 K was not considered when calculating the activation energy.

The position of the admittance waveforms in the double logarithmic coordinates was simultaneously influenced by the temperature dependence of the admittance value and admittance relaxation time. In the ultra-low frequency region, DC conductivity occurred. This was evidenced by Figure 2, from which it can be seen that for temperatures of 273 K and above, the phase shift angle was close to zero degrees. It follows that in this frequency region the admittance was determined by the resistance and its values did not depend on relaxation time. Its value depended only on the temperature through DC conductivity activation energy, given by the formula [33,34]:

$$\sigma (T)={\sigma }_0\exp \left(-\frac{\Delta W}{k\cdot T}\right),$$

(5)

where σ(T) is DC conductivity, σ₀ is constant value, ΔW is DC conductivity activation energy, k is Boltzmann constant, and T is temperature

The influence of the temperature dependence on the admittance value is clearly visible in the lowest frequency area of Figure 8. In this frequency range, for temperatures of 273.15 K and higher, the values of admittance did not depend on the frequency. This means that, in this frequency area, the admittance value did not depend on relaxation time. On the other hand, the increase of the admittance value with the increase in temperature was a result of the activation energy’s influence on admittance. In the ultra-low frequency area, including the frequency of 10⁻⁴ Hz, the admittance value depends on the temperature through the activation energy of admittance value. This eliminates the influence of the activation energy on admittance over the course of the admittance. Therefore, the Y(f) runs at 273.15–323.15 K were shifted to 293.15 K. The reference temperature in electrical engineering were 10⁻⁴ Hz and had equal admittance values (Figure 11). After such a shift, only the temperature dependence of the relaxation time had an effect on the waveforms shown in Figure 11.

For admittance analysis, the quantum phenomenon of electron tunneling between water droplets was used in this study. In [23], a relaxation time formula for electron tunneling was derived:

$$\tau \left(Y\right)={\tau }_0\exp \left(\frac{\beta \cdot r}{R_B}\right)\cdot \exp \left(\frac{\Delta W_Y}{kT}\right),$$

(6)

where β is numerical coefficient (the value of which, according to [35] was β ≈ (1.75 ± 0.05)), r is the distance between the wells of potentials produced by the nanodrops of water, R_B is the Bohr radius for the hopping electron, ∆W_Y is the activation energy of admittance, and r₀ is the numerical coefficient.

The measurement results, shown in Figure 11, were made for a sample containing 5% of moisture. This means that the average distance between the water nanoparticles was a constant value. Taking this fact into account, Formula (6) can be converted into:

$$\tau \left(Y\right)=C\left(\tau \right)\cdot \exp \left(\frac{\Delta W_{\tau Y}}{kT}\right),$$

(7)

where:

$$C\left(\tau \right)={\tau }_0\exp \left(\frac{\beta \cdot r}{R_B}\right)=const.$$

(8)

Formulas (7) and (8) show that in the tested sample, due to the constant concentration of potential wells—i.e., nanodrops of water—the relaxation time reduced to the known Formula (3) and depended only on temperature.

On the basis of FDS admittance measurements, we determined the relaxation time value with the accuracy of the numerical factor τ₀. For this purpose, the temperature shift of the admittance flows into a higher frequency area were analyzed. To determine the relaxation time value, we selected a specific value of admittance Y_i (Figure 11) and then read the frequency values at which this value occurred at different temperatures. The value of the relaxation time, to the nearest unspecified constant value, were identical for all temperatures (see Formulas (7) and (8)), which were determined by the formula:

$$\tau \left(Y_i\right)=\frac{\tau \left(T\right)}{{\tau }_0}=\frac{1}{2\cdot \pi \cdot f\left(Y_i\right)},$$

(9)

where f(Y_i) is the frequency at which the value of admittance Y_i at different temperatures occurs, τ(T) is the actual relaxation time, and τ₀ is an unspecified constant value equal for all temperatures.

In Figure 11, the area of changes in conductivity was marked with horizontal dashed lines, in which the growth segments of shifted annotations for measurement temperatures 273.15–323.15 K were located. On the basis of the results presented in Figure 11, frequency values were determined for 15 values of annotations from 10⁻⁹ S to 6.31 × 10⁻⁷ S, marked with dashed horizontal lines. Similarly to the case described above, for the phase shift angle, a large number of shift angle values were selected in order to determine with high accuracy the mean activation energies for relaxation time in the admittance and the uncertainty of its measurements. The obtained frequency values were used to prepare Arrhenius’ diagrams, presented in Figure 12. The linear approximation of Arrhenius’ diagrams, determined using the least squares method, proved their high accuracy since the determination coefficients R², calculated and presented in Table 2, ranged from 0.988 and above. and their mean value was R² ≈ (0.990 ± 0.0009). On the basis of approximation formulas for each run in Figure 12, the values of the activation energy for relaxation time in the admittance were determined, presented in Table 2. The mean value of the activation energy for relaxation time in the admittance was ΔWτ ≈ (0.796 ± 0.0139) eV.

Figure 13 shows 15 values of the activation energy for relaxation time in the admittance for values between 10⁻⁹ S and 6.31 × 10⁻⁷ S. As can be seen, the activation energy for relaxation time in the admittance was a constant value over a wide range of admittance changes.

3.3. Determination of the Activation Energy of Admittance

Once the activation energy for relaxation time in the admittance was obtained, its value was used to eliminate the effect of relaxation time on the frequency dependence of the admittance by shifting admittance curves along the X axis, as shown in Figure 8. For this purpose, the waveforms for 273.15 K, 283.15 K, 303.15 K, 313.15 K, and 323.15 K have been converted to the reference temperature of 293.15 K using ΔW_Y. The curves for 273.15 K and 283.15 K were shifted to a higher frequency area and for 303.15 K, 313.15 K, and 323.15 K to the lower frequency area (Figure 14). The curves for frequencies above 5 × 10⁻³ Hz were practically parallel. The values of all 6 shifted waveforms were in the frequency area from about 0.006 Hz to about 200 Hz, marked in Figure 14 with dashed vertical lines.

As was described in the cases above, 15 points on the frequency axis were selected to calculate the activation energy for the relaxation time of the phase shift angle and the admittance in the frequency range 5 × 10⁻³ Hz–200 Hz. This allowed for the accurate determination of the average value of activation energy in admittance and the uncertainty of its measurement. For each of these points, the admittance values occurring at different temperatures were determined. In total, 15 Arrhenius’ diagrams, shown in Figure 15, were drawn up. For the experimental points, we performed a linear approximation of the functions by the least square’s method, shown in Figure 15 as straight lines.

The quality of approximation was very high. The values of determination coefficients R², presented in Table 2, were within 0.992 to 0.995, and their mean value was 0.994 ± 0.0009. Regarding the obtained approximation formulas, the values of activation energy in admittance (Table 2) were determined for particular courses from Figure 15. The average activation energy value of admittance obtained on this basis was ∆W_Y ≈ (0.800 ± 0.0162) eV.

Figure 16 shows the frequency dependence of activation energy in admittance and the mean value ± standard deviation. The value of the activation energy in admittance was a constant value in a wide frequency range.

In total, 15 values for activation energy for relaxation time in the phase shift angle ΔW_φ, activation energy for relaxation time in the admittance ΔW_τ, and activation energy in admittance ∆W_Y are specified above (Table 2). A comparison of these values is shown in Figure 17.

The mean value of activation energy for relaxation time in the phase shift angle was ΔW_φ ≈ (0.783 ± 0.0744) eV, the activation energy for relaxation time in the admittance was ΔW_τ ≈ (0.796 ± 0.0139) eV, and the activation energy of admittance was ∆W_Y ≈ (0.800 ± 0.0162) eV. As can be seen, these values are close. The difference between the highest and lowest values was 0.017 eV. This was less than the standard deviation value (uncertainty of determination). This means that all three energy values describe different processes in cellulose composites, synthetic esters, and water nanoparticles, and are equal within the error limits. The mean value and standard deviation for the 45 residual activation energy values shown in Table 2 was ΔW ≈ (0.793 ± 0.0453) eV. From the comparison of this value with the activation energy value for alternating current conductivity (ΔW ≈ 1.0582 eV [27]) of the pressboard containing nanodrops of water and impregnated with transformer oil, it can be seen that the use of ester impregnation decreased activation energy by 0.26 eV. This was related to increased permittivity of esters compared to insulating oil.

The precise determination of activation energy opens up the possibility of converting the insulation parameters of transformers, which can be obtained at any operating temperature, into values at a reference temperature of 293.15 K (20 °C). This allows for the elimination of temperature influence on insulation parameters of transformers, as well as the separation of aging factors and other operating factors that may lead to deterioration.

4. Conclusions

The aim of this study was to investigate the phase shift angle and admittance of cellulose composites, synthetic esters, and water nanoparticles using FDS. The FDS method is widely used to diagnose insulation in power transformers and determine moisture content. Admittance and phase shift angle are the basic parameters of insulation, as determined by the FDS method. On the basis of the admittance value and the phase shift angle, it is possible to calculate the capacity and resistance of insulation in a parallel substitution scheme. Further, we calculated the material parameters of cellulose composites, synthetic esters, and water nanoparticles using the insulations geometrical dimensions.

The measurements were made in a frequency range of 10⁻⁴ Hz–5 × 10³ Hz with temperatures between 253.15 K and 323.15 K. A pressboard sample with 5% water content was selected for testing. Such a high water content was chosen because achieving it could have resulted in catastrophic failure of the power transformer. The model of step conductivity (electron tunneling) on direct and alternating currents was used to analyze the obtained results. It proved to be perfect for the analysis of the constant and alternating current results of the conductivity of cellulose composites, mineral oil, and water nanoparticles.

It was found that changes of the phase shift angle with frequency took place in two stages. The low-frequency stage was characterized by a faster phase shift angle change than the second, high-frequency stage. The activation energy values of relaxation times were determined for 15 values of phase shift angles, from −10° to −80°. The mean value of activation energy for relaxation time in the phase shift angle was ΔW_φ ≈ (0.783 ± 0.0744) eV.

Based on the analysis of admittance frequency waveforms obtained at different temperatures, we determined the activation energy for relaxation time in the admittance for 15 annotation values in the range 10⁻⁹ S to 6.31 × 10⁻⁷ S. Its mean value was ΔW_τ ≈ (0.796 ± 0.0139) eV. For 15 frequency values from the range 5×10⁻³ Hz to 200 Hz, the values of admittance activation energy were determined. The average value of activation energy in admittance was ∆W_Y ≈ (0.800 ± 0.0162) eV. It was found that all three activation energy values described different processes in cellulose composites, synthetic esters, and water nanoparticles, which were all equal within error limits. The mean value and standard deviation for 45 residual activation energy values was ΔW ≈ (0.793 ± 0.0453) eV.

Comparing this value with the value of activation energy for alternating conductivity in a pressboard containing nanodrops of water and impregnated with insulating oil shows that the use of ester impregnation results in a decrease of activation energy by 0.26 eV. This was due to the increased dielectric permittivity of the ester compared with insulating oil.