1. Introduction
Engineering applications with high heat flux generally involve boiling heat transfer. The high heat transfer coefficient reached by boiling flows makes boiling heat transfer relevant for research where thermal performance enhancement is needed. Although boiling heat transfer can improve the cooling performance of a system, the underlying physics are not fully understood yet. Therefore, it remains a major challenge to model the boiling heat transfer behavior for a boiling system.
Among other methods, the two-fluid model-based computational fluid dynamics (CFD) has shown a good capability of dealing with boiling flow heat transfer problems. In such an approach, information of the interface between vapor and liquid is taken as an average using closure equations, resulting in lower computational power requirements. Two-fluid models represent a promising solution to develop high fidelity representations, where all the concerned fields can be predicted with good accuracy. One of the most known two-fluid approach based CFD models to simulate boiling flows is the Rensselaer Polytechnic Institute (RPI) model, proposed by Kurul et al. [
1]. The RPI model proposes to decompose the total applied heat flux on the wall on three components to take into account the evaporation, forced convection, and the quenching. Many authors adopted this approach to model the boiling flows in different geometries and for multiple operating conditions [
2,
3,
4,
5]. When comparing their results to the available experimental data, fair agreements were obtained only for few fields, while bad estimations were obtained for many others. The fields of interest here are the vapor void fraction, the different phases velocities and temperatures, and the heated surface temperature. These failed estimations are related principally to the use of several closure models representing phenomenons occurring at different length scales, as the momentum and mass transfer at the interface, bubbles interaction in the bulk flow, and more importantly mechanical and thermal interactions on the heated surface, leading to nucleation, evaporation, bubble growth and departure, etc. These closure equations are developed based on empirical or mechanistic treatments. The first is based on experimental data that are valid only for reduced ranges of operating conditions, and when they are extrapolated, accurate results are no longer guaranteed. Mechanistic treatments are based on several assumptions that generally neglect the complicated interactions between bubbles, interactions between the heated surface and fluids, and they represent a hard linking between the occurring phenomenons time and space scales.
The field of fluid dynamics is closely linked to massive amounts of data from experiments and high-fidelity simulations. Big data in fluid mechanics has become a reality [
6] due to advancements in experimental techniques and high-performance computing (HPC). Machine learning (ML) algorithms are rapidly advancing within the fluid mechanics domain, and ML algorithms can be an additional tool for shaping, speeding up, and understanding complex problems that are yet to be fully solved. They provide a flexible framework that can be tailored for a particular problem, such as reduced-order modeling (ROM), optimization, turbulence closure modeling, heat transfer, or experimental data processing. For example, proper orthogonal decomposition (POD) has been successfully implemented to obtain a low-dimensional set of ordinary differential equations, from the Navier–Stokes equation, via Galerkin projection [
7,
8]. POD technique has been used to investigate the flow structures in the near-wall region based on measurements and information from the upper buffer layer at different Reynolds number for a turbulent channel [
9]. However, it has been reported that the POD method lacks in handling huge amount of data when the size of the computational domain increases [
10]. On the other hand, artificial neural networks (ANN) are capable of handling huge data size and nonlinear problems of near-wall turbulent flow [
11]. ANNs have been used to learn from large eddy simulation (LES) channel flow data, and it is capable of identifying and reproducing highly nonlinear behavior of the turbulent flows [
12]. In the last few years, there have been multiple studies related to the use of ANNs for estimating the subgrid-scale in turbulence modeling [
13,
14,
15]. Among other neural networks, convolution neural networks (CNNs) have been widely used for image processing due to their unique feature of capturing the spatial structure of input data [
16]. This feature is an advantage when dealing with fluid mechanics problems since CNN allows us to capture spatial and temporal information of the flows. Multiple CNN structure [
17] has been proposed to predict the lift coefficient of airfoils with different shapes at different Mach numbers, Reynolds number, and angle of attack. A combination of CNN with multi-layer perceptron (MLP) [
18] has been used to generate a time-dependent turbulent inflow generator for a fully developed turbulent channel flow. The data used for that work have been obtained from direct numerical simulation (DNS), and the model was able to predict the turbulent flow long enough to accumulate turbulent statistics.
Machine learning techniques are rapidly making inroads within heat transfer and multiphase problems too. These ML methods consist of a series of data-driven algorithms that can detect a pattern in large datasets and build predictive models. They are specially designed to deal with large, high-dimensional datasets, and have the potential to transform, quantify, and address the uncertainties of the model. ANN-based on the back-propagation model has been used to predict convective heat transfer coefficients in a tube with good accuracy [
19]. Experimental data from impingement jet with varying nozzle diameter and Reynolds number have been used to build an ANN model. This model was then used to predict the heat transfer (Nusselt number) with an error bellow 4.5% [
20]. More recently, researchers have used ANN for modeling boiling flow heat transfer of pure fluids [
21]. Neural networks have been used to fit DNS data to develop closure model relation for the average two-fluid equations of vertical bubble channel [
22]. The model trained on DNS data was then used for different initial velocities and void fraction, to predict the main aspects of DNS results. Different ML algorithms [
23] have been examined to study pool boiling heat transfer coefficient of aluminum water-based nanofluids, and their result showed that the MLP network gave the best result. In the past, CNNs model has been used even as an image processing technique for two-phase bubbly flow, and it has been shown that they can determine the overlapping of bubbles: blurred and nonspherical [
24].
Although there is research related to boiling heat transfer and machine learning algorithms, according to the authors’ knowledge all the above-mentioned models focus on deterministic ANN models. When working with a reduced order model or black-box model such as deep learning models for physical applications, it becomes of prime importance to know the model confidence and capability. If these models are to be used for a new set of operating conditions, the first thing to consider is how reliable this model is and how accurate the predicted value is. Therefore, it is crucial to know the uncertainty present in the predictions made.
The aforementioned ML techniques applied to heat transfer and fluid mechanics are mostly deterministic approaches that lack in providing predictive uncertainty information. At the same time, deterministic ANN models tend to produce overconfident predictions, which may lead to unpredictable situations when used in real-life industrial applications. Therefore, it is essential to quantify the uncertainty present in the model for any practical applications. Uncertainty models provide the user with the confidence level, and they allow them to make better decisions based on engineering judgment.
In Bayesian learning, a priori distribution is defined upon the parameters of a NNs, then given the training data, the posterior distribution over the parameter is computed, which is used to estimate the predictive uncertainty [
25]. The fundamental concern in Bayesian learning while analyzing data or making decisions is to be able to tell whether the model is certain about its output. Bayesian-based models offer a mathematically grounded framework to reason about model uncertainty, but the computational cost rapidly increases as the data size increases. Due to computational constraints in performing exact Bayesian inference, several approximation methods have been proposed such as; Markov chain Monte Carlo (MCMC) [
26] method, variational Bayesian methods [
27,
28], Laplace approximation [
29], probabilistic backpropagation (PBP) [
30]. The nature of predictive quality using Bayesian NNs depends on correct priori distribution and degree of approximation of Bayesian inference due to high computational cost [
31]. However, Bayesian models are harder to implement, they make it harder to define the correct priori properties, and they are computationally slower compared to traditional neural networks. Another approach to quantify the uncertainty of an ANN model is the Deep Ensemble method [
32], which is inspired by the bootstrap technique [
33]. In this method, it is assumed that the data has a parametrized distribution where the parameters depend on the input. Finding these parameters is the aim of the training process, i.e., the prediction network will not output a single value but instead will output the distributional parameters of the given input.
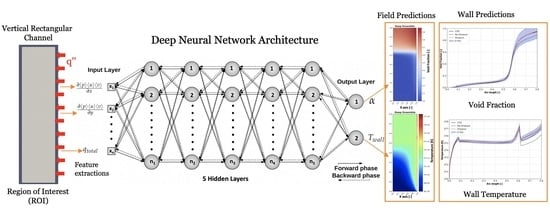
It is worth mentioning that this work presents one of the first attempts to implement deep learning techniques and quantify the model uncertainty of a data-driven subcooled boiling model. In this work, three data-driven models using deep learning techniques have been investigated to study the heat transfer behavior of a subcooled boiling in a minichannel with varying inflow velocity and heat fluxes. The first model focuses on the prediction of the deterministic value of the void fraction and wall temperature of the minichannel which are quantities of interest (QoIs). The second and third model focuses on probabilistic deep learning techniques to derive the uncertainty in the models when predicting the QoIs. The two methods used are Deep Ensemble, which is representative of the Maximum Likelihood approach, and Monte Carlo Dropout, which is representative of Bayesian inference. These two models are capable of capturing the nonlinear behavior that exists in the subcooled boiling data and is capable of reproducing the physics of unseen data for both interpolation and extrapolation datasets.
4. Conclusions
The objective of this study is twofold: firstly, to measure the accuracy of the predictions of the deep learning models compared to the CFD results and secondly to quantify the confidence level of the predictions. In this work, three supervised deep learning models have been investigated to study the subcooled boiling heat transfer in a vertical minichannel. The first method focuses on the deterministic approach, whereas the second and the third focus on the probabilistic approach to quantify the uncertainty present in the model while predicting the outputs (QoIs). The training data are obtained from CFD simulations based on the Eulerian two-fluid approach, for varying heat fluxes and inlet velocities. In total 102 cases were simulated, out of which 96 cases were used for training (80%) and validation (20%), and the remaining 6 cases were purely used for in-depth evaluation of the model’s interpolation and extrapolation performance.
The models presented in this study showed a good level of accuracy while predicting the void fraction and the wall temperature. However, it has been observed that the deterministic model (standard DNN/ MLP) showed lower performance when predicting the wall temperature and void fraction. It is crucial to be able to justify the predictive nature and the uncertainty present in the model. Therefore, the probabilistic models’ Monte Carlo Dropout and Deep Ensemble methods were investigated to quantify the predictive uncertainty and the confidence level of these DNNs. The output obtained from these probabilistic models is presented in the form of normal distribution rather than a deterministic value, from which the mean value and the variance of the predicted values are calculated.
According to the results presented, it can be stated that both the MC Dropout and Deep Ensemble models were able to capture the physics well from the given training data. Furthermore, they were able to reproduce these physics on unseen interpolation and extrapolation dataset. The predicted mean values, i.e., the void fraction and the wall temperature were very close to the CFD results and both performed better than the deterministic MLP model. In particular, the DE model showed exceptional predictive performance with low uncertainty. It is worth highlighting that both models were able to capture the change in boiling regimes accurately and showed higher uncertainty when there is a sudden shift in physics, for example when the nucleation starts in the minichannel. Moreover, the probabilistic models were able to reproduce the physics with good accuracy on an extreme extrapolation dataset at a heat flux of = 40,000 Wm, even though the maximum heat flux used while training the models was 29,000 Wm. The uncertainty quantification of the models further explains the steep change in void fraction and wall temperature when heat flux and inflow velocity are varied. On average, all the models had a error under 5% for the wall temperature and error under 2% for the void fraction with coefficient of determination and , respectively. This shows that the current study can capture the underlying physics that exist in the boiling data and serves as an independent method to predict the QoIs for a new case study.
The only shortcoming of the uncertainty models compared to the standard MLP model is the computational speed, the predictive time of the uncertainty models are one order of magnitude slower compared to the deterministic MLP model. Nevertheless, the predictive time for the uncertainty models are still two orders of magnitude faster than CFD simulation. The predictive speed of uncertainty models is acceptable considering it provides better performance with the confidence levels and is reasonable for the system-level design process. Therefore, the DNN with uncertainty models can be used as a promising tool to speed up the design phase/initial guesses in the thermal management of a subcooled boiling system.