Effects of Input Voltage and Freestream Velocity on Active Flow Control of Passage Vortex in a Linear Turbine Cascade Using Dielectric Barrier Discharge Plasma Actuator
Abstract
:1. Introduction
2. Experimental Methods
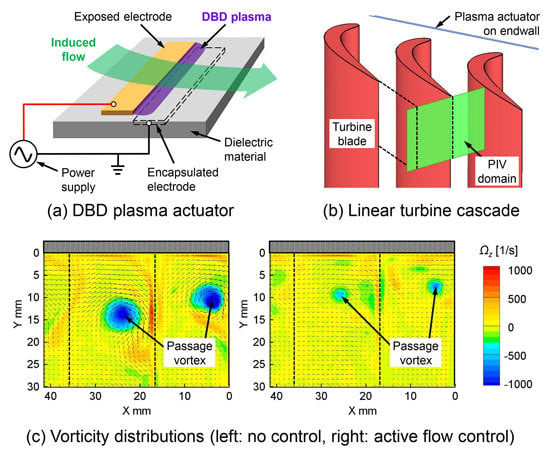
2.1. Wind Tunnel and Linear Turbine Cascade
2.2. Particle Image Velocimetry (PIV) Measurements and Data Processing
2.3. Plasma Actuator
3. Characteristics of Plasma Actuator
4. Results and Discussion
4.1. Measurements at Outlet Freestream Velocity of 2.4 m/s, Reout = 1.0 × 104
4.2. Measurements at Outlet Freestream Velocity of 4.7 m/s, Reout = 1.9 × 104
4.3. Measurements at Higher Outlet Freestream Velocity from 9.4 m/s to 25.2 m/s, Reout = 3.7 × 104–9.9 × 104
5. Conclusions
- At the lowest freestream velocity condition of UFS,out = 2.4 m/s, the passage vortex was completely eliminated by the plasma actuator operation at VAC = 10 kVp-p (UPA,max/UFS,out = 1.17). The maximum reductions of the peak values of the velocity and vorticity of the passage vortex by the plasma actuator were 55% and 74%, respectively.
- At the freestream velocity condition of UFS,out = 4.7 m/s, the passage vortex was reduced by the plasma actuator operation at VAC = 15 kVp-p (UPA,max/UFS,out = 0.96). The maximum reductions of the peak values of the velocity and vorticity of the passage vortex by the plasma actuator were 21% and 47%, respectively.
- The effects of jet induced by the plasma actuator weakened as the freestream velocity increased.
- At the highest freestream velocity condition of UFS,out = 25.2 m/s, the peak value of the vorticity was reduced about 17% by the plasma actuator operation at VAC = 15 kVp-p (UPA,max/UFS,out = 0.18).
Author Contributions
Funding
Conflicts of Interest
References
- Lakshminarayana, B. Fluid Dynamics and Heat Transfer of Turbomachinery; John Wiley & Sons, Inc.: New York, NY, USA, 1996; p. 324. [Google Scholar] [CrossRef]
- Sharma, O.P.; Butler, T.L. Predictions of Endwall Losses and Secondary Flows in Axial Flow Turbine Cascades. J. Turbomach. 1987, 109, 229–236. [Google Scholar] [CrossRef]
- Coull, J.; Clark, C.; Vazquez, R. The sensitivity of turbine cascade endwall loss to inlet boundary layer thickness. J. Glob. Power Propuls. Soc. 2019, 3, 540–554. [Google Scholar] [CrossRef]
- Langston, L.S. Crossflows in a Turbine Cascade Passage. J. Eng. Power 1980, 102, 866–874. [Google Scholar] [CrossRef]
- Sieverding, C.H. Recent Progress in the Understanding of Basic Aspects of Secondary Flows in Turbine Blade Passages. J. Eng. Gas Turbines Power 1985, 107, 248–257. [Google Scholar] [CrossRef]
- Wang, H.P.; Olson, S.J.; Goldstein, R.J.; Eckert, E.R.G. Flow Visualization in a Linear Turbine Cascade of High Performance Turbine Blades. J. Turbomach. 1997, 119, 1–8. [Google Scholar] [CrossRef]
- Coull, J.D. Endwall Loss in Turbine Cascades. J. Turbomach. 2017, 139. [Google Scholar] [CrossRef]
- Bons, J.P.; Sondergaard, R.; Rivir, R.B. Turbine Separation Control Using Pulsed Vortex Generator Jets. J. Turbomach. 2001, 123, 198–206. [Google Scholar] [CrossRef]
- Hodson, H.P.; Dominy, R.G. The Off-Design Performance of a Low-Pressure Turbine Cascade. J. Turbomach. 1987, 109, 201–209. [Google Scholar] [CrossRef]
- Ainley, D.G.; Mathieson, G.C.R. A Method of Performance Estimation for Axial-Flow Turbines; British Aeronautical Research Council: London, UK, 1951. [Google Scholar]
- Matsunuma, T.; Abé, H.; Tsutsui, Y. Influence of Turbulence Intensity on Annular Turbine Stator Aerodynamics at Low Reynolds Numbers. In Proceedings of the ASME 1999 International Gas Turbine and Aeroengine Congress and Exhibition, Indianapolis, IN, USA, 7–10 June 1999. [Google Scholar]
- Aramendia, I.; Fernandez-Gamiz, U.; Ramos-Hernanz, J.A.; Sancho, J.; Lopez-Guede, J.M.; Zulueta, E. Flow Control Devices for Wind Turbines. Lect. Notes Energy 2017, 37, 629–655. [Google Scholar]
- Schmid, J.; Schulz, A.; Bauer, H.-J. Influence of a Non-Axisymmetric Endwall on the Flow Field in a Turbine Passage: High-Resolution LDV. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018. [Google Scholar] [CrossRef]
- Sangston, K.; Little, J.; Lyall, M.E.; Sondergaard, R. End Wall Loss Reduction of High Lift Low Pressure Turbine Airfoils Using Profile Contouring—Part 2: Validation. J. Turbomach. 2014, 136. [Google Scholar] [CrossRef]
- Chung, J.T.; Simon, T.W.; Buddhavarapu, J. Three-Dimensional Flow Near the Blade/Endwall Junction of a Gas Turbine: Application of a Boundary Layer Fence. In Proceedings of the ASME 1991 International Gas Turbine and Aeroengine Congress and Exposition, Orlando, FL, USA, 3–6 June 1991. [Google Scholar]
- Wei, Z.; Cui, Y.; New, T.H. An experimental study on flow separation control of hydrofoils with leading-edge tubercles at low Reynolds number. Ocean Eng. 2015, 108, 336–349. [Google Scholar] [CrossRef]
- Shyam, V.; Ameri, A.; Poinsatte, P.; Thurman, D.; Wróblewski, A.; Snyder, C. Application of Pinniped Vibrissae to Aeropropulsion. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015. [Google Scholar]
- Bloxham, M.J.; Bons, J.P. A Global Approach to Turbomachinery Flow Control: Passage Vortex Control. J. Turbomach. 2014, 136. [Google Scholar] [CrossRef]
- Benton, S.I.; Bons, J.P.; Sondergaard, R. Secondary Flow Loss Reduction Through Blowing for a High-Lift Front-Loaded Low Pressure Turbine Cascade. J. Turbomach. 2013, 135. [Google Scholar] [CrossRef]
- Benton, S.I.; Bernardini, C.; Bons, J.P.; Sondergaard, R. Parametric Optimization of Unsteady End Wall Blowing on a Highly Loaded Low-Pressure Turbine. J. Turbomach. 2014, 136. [Google Scholar] [CrossRef]
- Bons, J.; Benton, S.; Bernardini, C.; Bloxham, M. Active Flow Control for Low-Pressure Turbines. AIAA J. 2018, 56, 2687–2698. [Google Scholar] [CrossRef]
- Roth, J.R.; Sherman, D.M.; Wilkinson, S.P. Boundary Layer Flow Control with a One Atmosphere Uniform Grow Discharge. AIAA Pap. 1998. [Google Scholar] [CrossRef] [Green Version]
- Corke, T.C.; Post, M.L.; Orlov, D.M. SDBD plasma enhanced aerodynamics: Concepts, optimization and applications. Prog. Aerosp. Sci. 2007, 43, 193–217. [Google Scholar] [CrossRef]
- Corke, T.C.; Enloe, C.L.; Wilkinson, S.P. Dielectric Barrier Discharge Plasma Actuators for Flow Control. Annu. Rev. Fluid Mech. 2010, 42, 505–529. [Google Scholar] [CrossRef]
- Wang, J.-J.; Choi, K.-S.; Feng, L.-H.; Jukes, T.N.; Whalley, R.D. Recent developments in DBD plasma flow control. Prog. Aerosp. Sci. 2013, 62, 52–78. [Google Scholar] [CrossRef]
- Shyy, W.; Jayaraman, B.; Andersson, A. Modeling of glow discharge-induced fluid dynamics. J. Appl. Phys. 2002, 92, 6434–6443. [Google Scholar] [CrossRef]
- Suzen, Y.; Huang, G.; Jacob, J.; Ashpis, D. Numerical Simulations of Plasma Based Flow Control Applications. In Proceedings of the 35th AIAA Fluid Dynamics Conference and Exhibit, Toronto, ON, Canada, 6–9 June 2005. [Google Scholar]
- Fujii, K. High-performance computing-based exploration of flow control with micro devices. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Babou, Y.; Martin, E.N.; Peña, P.F. Simple Body Force Model for Dielectric Barrier Discharge Plasma Actuator. In Proceedings of the 7th European Conference for Aeronautics and Aerospace Sciences (EUCASS), Milan, Italy, 3–6 July 2017; EUCASS AISBL: Rhode-Saint-Genèse, Belgium. [Google Scholar] [CrossRef]
- Huang, J.; Corke, T.C.; Thomas, F.O. Plasma Actuators for Separation Control of Low-Pressure Turbine Blades. AIAA J. 2006, 44, 51–57. [Google Scholar] [CrossRef]
- Huang, J.; Corke, T.C.; Thomas, F.O. Unsteady Plasma Actuators for Separation Control of Low-Pressure Turbine Blades. AIAA J. 2006, 44, 1477–1487. [Google Scholar] [CrossRef]
- Rizzetta, D.; Visbal, M. Numerical Investigation of Plasma-Based Flow Control for a Transitional Highly-Loaded Low-Pressure Turbine. AIAA J. 2007. [Google Scholar] [CrossRef]
- Pescini, E.; Marra, F.; De Giorgi, M.G.; Francioso, L.; Ficarella, A. Investigation of the boundary layer characteristics for assessing the DBD plasma actuator control of the separated flow at low Reynolds numbers. Exp. Therm. Fluid Sci. 2017, 81, 482–498. [Google Scholar] [CrossRef]
- Martinez, D.S.; Pescini, E.; Marra, F.; De Giorgi, M.G.; Ficarella, A. Analysis of the Performance of Plasma Actuators Under Low-Pressure Turbine Conditions Based on Experiments and URANS Simulations. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar]
- Van Ness, D.; Corke, T.; Morris, S. Turbine Tip Clearance Flow Control Using Plasma Actuators. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar]
- Van Ness, D.; Corke, T.; Morris, S. Stereo PIV of a Turbine Tip Clearance Flow with Plasma Actuation. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. [Google Scholar]
- Van Ness, D.K.; Corke, T.C.; Morris, S.C. Tip Clearance Flow Visualization of a Turbine Blade Cascade with Active and Passive Flow Control. In Proceedings of the ASME Turbo Expo 2008: Power for Land, Sea and Air, Berlin, Germany, 9–13 June 2008; pp. 1217–1229. [Google Scholar]
- Stephens, J.E.; Corke, T.; Morris, S. Blade-Mounted Single Dielectric Barrier Discharge Plasma Actuators in Turbine Cascade. J. Propuls. Power 2011, 27, 692–698. [Google Scholar] [CrossRef]
- Matsunuma, T.; Segawa, T. Active Tip Clearance Flow Control for an Axial-Flow Turbine Rotor Using Ring-Type Plasma Actuators. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. [Google Scholar]
- Matsunuma, T.; Segawa, T. Tip Leakage Flow Reduction of a Linear Turbine Cascade Using String-Type DBD Plasma Actuators. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018. [Google Scholar]
- Yu, J.; Bao, W.; Chen, F.; Song, Y.; Wang, C. Optimization and Evaluation of Multiple DBD Plasma Actuators Applied in the Tip Leakage Control for Turbine Cascade. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019. [Google Scholar]
- Yu, J.; Yu, J.; Chen, F.; Wang, C. Numerical study of tip leakage flow control in turbine cascades using the DBD plasma model improved by the parameter identification method. Aerosp. Sci. Technol. 2019, 84, 856–864. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Traficante, S.; De Luca, C.; Bello, D.; Ficarella, A. Active Flow Control Techniques on a Stator Compressor Cascade: A Comparison Between Synthetic Jet and Plasma Actuators. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012. [Google Scholar]
- Matsunuma, T. Effects of Reynolds Number and Freestream Turbulence on Turbine Tip Clearance Flow. J. Turbomach. 2006, 128, 166–177. [Google Scholar] [CrossRef]
- Matsunuma, T. Unsteady Flow Field of an Axial-Flow Turbine Rotor at a Low Reynolds Number. J. Turbomach. 2007, 129, 360–371. [Google Scholar] [CrossRef]
- Montis, M.; Niehuis, R.; Fiala, A. Aerodynamic Measurements on a Low Pressure Turbine Cascade With Different Levels of Distributed Roughness. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011. [Google Scholar]
- Bons, J.P. A Review of Surface Roughness Effects in Gas Turbines. J. Turbomach. 2010, 132. [Google Scholar] [CrossRef]
- Vázquez, R.; Torre, D.; Partida, F.; Armañanzas, L.; Antoranz, A. Influence of Surface Roughness on the Profile and End-Wall Losses in Low Pressure Turbines. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011. [Google Scholar]
- Kriegseis, J.; Möller, B.; Grundmann, S.; Tropea, C. Capacitance and power consumption quantification of dielectric barrier discharge (DBD) plasma actuators. J. Electrost. 2011, 69, 302–312. [Google Scholar] [CrossRef]
- Ashpis, D.E.; Laun, M.C.; Griebeler, E.L. Progress toward accurate measurements of power consumptions of DBD plasma actuators. AIAA Pap. 2011. [Google Scholar] [CrossRef]
- Murphy, J.P.; Kriegseis, J.; Lavoie, P. Scaling of maximum velocity, body force, and power consumption of dielectric barrier discharge plasma actuators via particle image velocimetry. J. Appl. Phys. 2013, 113. [Google Scholar] [CrossRef]
- Hanson, R.E.; Houser, N.M.; Lavoie, P. Dielectric material degradation monitoring of dielectric barrier discharge plasma actuators. J. Appl. Phys. 2014, 115. [Google Scholar] [CrossRef]
- Technical Section on Plasma Actuators—Activities in the Past 5 Years and Future Prospects. Available online: http://www.jsme-fed.org/newsletters-e/2019_2/no3.html (accessed on 23 December 2019).

























| Parameter | Symbol | Value |
|---|---|---|
| Number of blades | N | 6 |
| Chord length | C | 58.65 mm |
| Axial chord length | Cax | 49.43 mm |
| Blade height | H | 75.00 mm |
| Blade pitch | S | 35.47 mm |
| Inlet flow angle | α1 | 51.86° |
| Outlet flow angle | α2 | 58.74° |
| Turning angle | α1 + α2 | 110.60° |
| Stagger angle | ξ | 33.43° |
| Rotating Speed of Blower [Hz] | Inlet Velocity UFS,in [m/s] | Outlet Velocity UFS,out [m/s] | Reynolds Number Reout |
|---|---|---|---|
| 113 | 2.0 | 2.4 | 1.0 × 104 |
| 225 | 3.9 | 4.7 | 1.8 × 104 |
| 450 | 7.9 | 9.4 | 3.7 × 104 |
| 675 | 12.3 | 14.6 | 5.7 × 104 |
| 900 | 17.6 | 20.9 | 8.2 × 104 |
| 1125 | 21.2 | 25.2 | 9.9 × 104 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matsunuma, T.; Segawa, T. Effects of Input Voltage and Freestream Velocity on Active Flow Control of Passage Vortex in a Linear Turbine Cascade Using Dielectric Barrier Discharge Plasma Actuator. Energies 2020, 13, 764. https://doi.org/10.3390/en13030764
Matsunuma T, Segawa T. Effects of Input Voltage and Freestream Velocity on Active Flow Control of Passage Vortex in a Linear Turbine Cascade Using Dielectric Barrier Discharge Plasma Actuator. Energies. 2020; 13(3):764. https://doi.org/10.3390/en13030764
Chicago/Turabian StyleMatsunuma, Takayuki, and Takehiko Segawa. 2020. "Effects of Input Voltage and Freestream Velocity on Active Flow Control of Passage Vortex in a Linear Turbine Cascade Using Dielectric Barrier Discharge Plasma Actuator" Energies 13, no. 3: 764. https://doi.org/10.3390/en13030764
APA StyleMatsunuma, T., & Segawa, T. (2020). Effects of Input Voltage and Freestream Velocity on Active Flow Control of Passage Vortex in a Linear Turbine Cascade Using Dielectric Barrier Discharge Plasma Actuator. Energies, 13(3), 764. https://doi.org/10.3390/en13030764