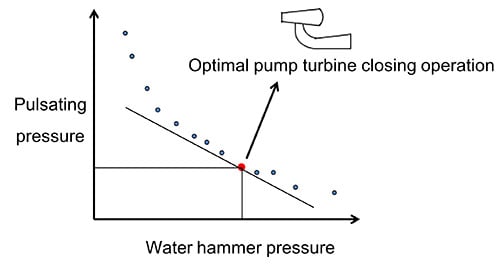
Optimization of Pump Turbine Closing Operation to Minimize Water Hammer and Pulsating Pressures During Load Rejection

Abstract

In load rejection transitional processes in pumped-storage plants (PSPs), the process of closing pump turbines, including guide vane (GVCS) and ball valve closing schemes (BVCS), is crucial for controlling pulsating pressures and water hammer. Extreme pressures generated during the load rejection process may result in fatigue damage to turbines, and cracks or even bursts in the penstocks. In this study, the closing schemes for pump turbine guide vanes and ball valves are optimized to minimize water hammer and pulsating pressures. A model is first developed to simulate water hammer pressures and to estimate pulsating pressures at the spiral case and draft tube of a pump turbine. This is combined with genetic algorithms (GA) or non-dominated sorting genetic algorithm II (NSGA-II) to realize single- or multi-objective optimizations. To increase the applicability of the optimized result to different scenarios, the optimization model is further extended by considering two different load-rejection scenarios: full load-rejection of one pump versus two pump turbines, simultaneously. The fuzzy membership degree method provides the best compromise solution for the attained Pareto solutions set in the multi-objective optimization. Employing these optimization models, robust closing schemes can be developed for guide vanes and ball valves under various design requirements.

1. Introduction

In recent years, pumped-storage power plants (PSPs) have become increasingly important in stabilizing and balancing electricity [1,2,3]. They play the roles of frequency regulation, peak shaving, and emergency power supply in a power grid. PSPs are intricate nonlinear systems typically consisting of pipelines, pump turbines, ball valves, reservoirs, and surge tanks. To better present the PSP system in this paper, a basic configuration of a real PSP in China is shown in Figure 1.

To fulfill the above functions, a PSP system has to constantly undergo various transient processes. Load rejection in turbine mode is one of the challenging working conditions threatening the safety of the PSP. When full load rejection occurs, the governor will quickly close the guide vanes. The operating points of pump turbine will go through a so-called reverse-S-shaped region, which may cause a series of instability problems [4,5]. In this case, the water hammer at the spiral case may reach an extremely high level, leading to abnormal vibration and penstock failure, and the pressure at the draft tube may reach an extremely low level, leading to cavitation and even water column separation. Additionally, pulsating pressures, a fluctuation component upon water hammer pressures, may also increase largely when operating in the S-shaped region [6]. The existence of this kind of pressure is one of the main reasons for unit vibration as well as fatigue damage of pump turbines [7,8]. Therefore, minimizing both water hammer and pulsating pressures during load rejection is of great importance to ensure the safety and stability of PSPs.

The optimization of guide vane closing schemes (GVCSs) is an important strategy to reduce water hammer pressure and pulsating pressures. Traditionally, a slower guide vane closure means lower water hammer pressure, but a higher rotational speed rise which is often accompanied by larger pulsating pressures. Thus, an optimal GVCS is significant to coordinate the trade-off between them. A lot of research has been done on the GVCS optimization previously. Vakil [9] examined different guide vane closing laws to investigate their effects on pressure rise and speed rise. Zhang et al. [10] introduced a joint closing scheme of guide vane and ball valve in load rejection and indicated that the joint closing scheme can effectively reduce the second pressure peak at the spiral case. Zeng et al. [11] theoretically analyzed the effects of the GVCS on water hammer and pulsating pressures based on the transient characteristics of pump turbines in the S-shaped region.

In addition to those theoretical analyses of the transient process, evolutionary algorithms have also been widely used to seek optimal closing schemes for pump turbines [12,13]. Considering water hammer pressure and speed rise, Zhou et al. [14] solved the GVCS optimization problem using an enhanced multi-objective gravitational search algorithm. Lai et al. [15] conducted the optimization with guide vanes closing in different ways, and they found that the three-stage GVCS achieved better performance in hydraulic transient simulations than the traditional one- or two-stage GVCSs.

Overall, previous studies have done a large number of optimizations based on the evolutionary algorithms using the speed rise and water hammer as objective functions in transient processes, but there is no existing research on optimization for minimizing pulsating pressures of a pump turbine. One reason for this is that it is difficult to model pulsating pressures in one-dimensional flow owing to their obvious three-dimensional characteristics [16,17]. However, as the authors have mentioned above, pulsating pressures control in extreme conditions is necessary, especially when the speed rise within its threshold. Without considering pulsating pressures, the results of previous work may be limited in practical application.

To overcome the shortcomings in existing GVCS optimization, this paper introduces a method of peak-to-peak diagrams [18] into the transient model to estimate dynamic pulsating pressures. The proposed model was then combined with genetic algorithms (GAs) using water hammer and pulsating pressures instead of speed rise as the objective functions. To obtain reliable and applicable closing schemes, both single-objective and multi-objective optimization of GVCS and BVCS are carried out in load rejection in the PSP. The innovations of this research include the following; (1) a method of peak-to-peak diagrams is applied to estimate dynamic pulsating pressures, (2) new objective functions considering water hammer and pulsating pressures are designed to meet different engineering requirements, and (3) both single load rejection and load rejection of two units are incorporated within the optimization model to broaden the applicability of the optimized results.

The remainder of this article is organized as follows. Section 2 constructs the hydraulic transient model, including the method to estimate dynamic pulsating pressures. Section 3 describes the formulation for optimizing the pump turbine closing operation by means of evolutionary algorithms. In Section 4, the transient model is validated with field test results. Then, three cases are carried out to optimize the pump turbine closing operation and the results are presented with the corresponding analyses. Section 5 summarizes the main results and presents conclusions.

2. Hydraulic Transient Simulation with Pulsating Pressure Estimation

Figure 1 shows a typical kind of PSP system with two pump turbines sharing the same main pipelines. To ensure the safe and reliable operation of the pump turbine, the inlet of each pump turbine is equipped with a ball valve. Based on the actual installation, two surge tanks are adopted to control transient in this system.

In this section, the hydraulic transient model based on the method of characteristics (MOC) is first established to calculate water hammer pressure. The models of pipeline system, pump turbine, and ball valve are briefly introduced, and more detailed information can also be found in the literature [19,20,21]. Then a method of peak-to-peak diagrams is proposed to estimate pulsating pressures.

2.1. Pipeline System Model

In the case of unsteady compressible liquid flow in elastic pressurized pipelines, governing equations can be considered as

$$\frac{\partial V}{\partial t}+g\frac{\partial H}{\partial x}+\frac{fV\left|V\right|}{2D}=0$$

(1)

$$\frac{\partial H}{\partial t}+\frac{a^2}{g}\frac{\partial V}{\partial x}=0$$

(2)

where $H$ is the piezometric head, $V$ is flow velocity, $x$ is the distance along the pipeline, and $t$ is time; $a$ is wave speed, $g$ is gravitational acceleration, $D$ is the pipe diameter, and $f$ is the Darcy–Weisbach friction factor.

To solve the above partial differential equations, the method of characteristics described in [22] is employed as the numerical method for the pipeline system. This method, in essence, transforms Equations (1) and (2) into an ordinary differential equation set in the range of the characteristic lines. Along the right line $C^{+} \left(\frac{dx}{dt}=a\right)$ and left line $C^{-} \left(\frac{dx}{dt}=-a\right)$ (Figure 2), the flow and head in the pipelines satisfy Equations (3) and (4):

$$C^{+}: \frac{dH}{dt}+\frac{a}{gA}\frac{dQ}{dx}+\frac{af}{2gD{A}^2}Q\left|Q\right|=0$$

(3)

$$C^{-}: \frac{dH}{dt}-\frac{a}{gA}\frac{dQ}{dx}-\frac{af}{2gD{A}^2}Q\left|Q\right|=0$$

(4)

where $Q$ is the flow rate. Therefore, the finite difference method can be used to obtain Equations (5) and (6) for unknown $H_{\mathrm{P}}$ and $Q_{\mathrm{P}}$

$$\left(H_P-H_A\right)+\frac{a}{gA}\left(Q_P-Q_A\right)+\frac{af}{2gD{A}^2}{{\displaystyle \int }}_A^{P}Q\left|Q\right|dx=0$$

(5)

$$\left(H_P-H_B\right)-\frac{a}{gA}\left(Q_P-Q_B\right)-\frac{af}{2gD{A}^2}{{\displaystyle \int }}_B^{P}Q\left|Q\right|dx=0$$

(6)

2.2. Pump Turbine Model

In this paper, a validated pump turbine model presented in [19] is introduced based on its characteristic curves. In this case, the flow function and torque function are described by flow characteristic curves (in Figure 3a) and torque characteristic curves (Figure 3b). Consequently, the mathematical model of pump turbine can be written as

$$\{\begin{array}{c}{Q}_{11}=f_Q\left(y,n_{11}\right) \\ M_{11}=f_M\left(y,n_{11}\right) \\ n_{11}=\frac{n{D}_1}{\sqrt{H}} \\ Q_{11}=\frac{Q}{{D_1}^2\sqrt{H}} \\ M_{11}=\frac{M}{{D_1}^3\sqrt{H}} \\ J\frac{\pi }{30}\frac{dn}{dt}= M-M_g\end{array}$$

(7)

where $f_Q$ and $f_M$ denote the interpolation functions between flow characteristic curves and torque characteristic curves, respectively, with the guide vane opening y (GVO) and the unit rotational speed $n_{11}$ as the inputs; $Q_{11}$ and $M_{11}$ represent the unit flow and unit torque, respectively; $n$ is rotational speed, and $Q$ and $M$ are the flow rate and the torque of the pump turbine, respectively; $D_1$ is the inlet diameter of the runner $H$ is the water head, $J$ is the generator moment of inertia, and $M_g$ is the load moment, which is equal to 0 in load rejection.

Figure 3 shows a part of the characteristic curves which were provided by the manufacturer through model tests. However, the characteristic curves exhibit a reverse “S” shape, crossover, and overlap between each other (as shown in the ellipses in Figure 3), which may cause multi-value problems in the interpolation. Thus, an improved Suter transformation method in [23] is employed to exact the uneven characteristic curves.

2.3. Ball Valve Model

The ball valve should also be closed immediately in case of an emergency shutdown of the unit to ensure that the pulsating pressure does not exceed the specified value. The mathematical model of ball valve is

$$Q_{bv}=(C_{d}A)\sqrt{2g\Delta H_{bv}}$$

(8)

where $Q_{bv}$ is the flow of ball valve; $C_d$ and $A$ is the coefficient of flow and area of ball valve opening (BVO), respectively; and $\Delta H_{bv}$ is the head difference between upstream and downstream of the ball valve. In practice, the function $C_{d}A$ is normally considered as a parameter changing with BVO.

2.4. Estimating Dynamic Pulsating Pressures

The above hydraulic transient model is capable of calculating water hammer pressures, but not of calculating pulsating pressures. Thus, this paper applied a method of peak–peak diagrams into the transient model for estimating pulsating pressures.

Figure 4 shows the used peak–peak diagrams provided by the manufacturer. They demonstrate the contours of the pulsating pressures in the spiral case (Figure 4a) and in the draft tube (Figure 4b) of the pump turbine. Each contour line corresponds to a specific relative amplitude of pulsating pressure. The amplitude of the pulsating pressures increases in the turbine‘s working region, reaching its maximum around the runaway curve.

Based on the peak-to-peak diagrams, the estimation of pulsating pressures can be divided into three stages:

(1) Extension of contour lines

The data of pulsating pressure in pump turbine model tests usually include only the turbine operation area, but the operating points of load rejection have to experience braking region (from runaway to zero flow) and reverse-pumping region (after zero flow). To obtain the pulsating pressure contour map of the above region, the contour lines are extended according to its distribution and trend. Figure 5 gives the extended contour lines.

(2) Interpolation of the relative amplitude of pulsating pressure

Then, by plotting the operational trajectory on the peak-to-peak diagrams, the relative amplitude of pulsating pressure for each operating point can be interpolated. The relative amplitude of pulsating pressure is expressed as

$$\alpha =f_i\left(n_{11},Q_{11}\right)$$

(9)

where $\alpha$ is the relative amplitude of pulsating pressure and $f_i$ is the function of interpolation. In this paper, the interpolation algorithm in map design [24] is adopted for $f_i$.

(3) Calculation of pulsating pressure magnitude

Finally, transforming the relative amplitude into absolute magnitude by Equation (10), the magnitude variation of pulsating pressures can then be estimated.

$$\Delta P=\frac{1}{2}\alpha H$$

(10)

where $\Delta P$ is the pulsating pressure magnitude, which is half the peak-to-peak value, and $H$ is the water head of the pump turbine. Figure 6 shows the architecture of pulsating pressure estimation based on peak-peak diagrams.

3. Formulations for Optimization of Pump Turbine Closing Process

Based on the hydraulic transient model, both the genetic algorithm (GA) and non-dominated sorting genetic algorithm (NSGA-II) are employed to optimize GVCS and BVCS in load rejection. Single-objective [25,26] and multi-objective optimization cases [12,14,27] are considered to meet various engineering requirements. The water hammer and pulsating pressures are synthesized into the total dynamic pressure in the single-objective optimization. In comparison, the multi-objective optimization leads to a set of Pareto non-dominated solutions that can give the operator more flexible choices according to the actual onsite conditions.

3.1. Closing Strategies

Multiple closing strategies are considered in this study, including two-stage GVCS, three-stage GVCS, and GVCS combined with BVCS. Schematics of the two-stage and three-stage GVCSs are shown in Figure 7, with BVCS only adopting the two-stage scheme.

The initial opening and the total closing time of valves are set to be constants. Therefore, the decision variables can be defined by the coordinates of inflection points. According to the closing strategies, the decision vectors are formulated as (1) two-stage GVCS, $D_1=\left[t_{g1} y_{g1}\right]$; (2) three-stage GVCS, $D_2=\left[t_{g1} y_{g1} t_{g2} y_{g2}\right]$; (3) two-stage GVCS with BVCS, $D_3=\left[t_{g1} y_{g1} t_b y_b\right]$; and (4) three-stage GVCS with BVCS, $D_4=\left[t_{g1} y_{g1} t_{g2} y_{g2} t_b y_b\right]$, where $t_{g1}$ and $y_{g1}$ are the abscissa and ordinate of the first inflection point of the guide vane closing curve, $t_{g2}$ and $y_{g2}$ are the abscissa and ordinate of the second inflection point of the guide vane closing curve, and $t_b$ and $y_b$ are the abscissa and ordinate of the inflection point of the ball valve closing curve.

3.2. Objective Functions

When designing PSPs, the total dynamic pressures at the inlet of the spiral case and the outlet of the draft tube during load-rejection scenarios are crucial. The maximum pressure at the spiral case determines the required structural strength of the pipelines, and the minimum pressure at the draft tube needs to exceed the vapor pressure in order to avoid separation of the fluid column, which may generate a huge pressure surge in the draft tube. Thus, the first objective function considers the total dynamic pressures and is defined as

$$MinOb{j}_1=max\left\{P_s+\Delta P_s\right\}-min\left\{P_d-\Delta P_d\right\}$$

(11)

where $P_s$ and $P_d$ are the water hammer pressures at the spiral case and draft tube, respectively, and $\Delta P_s$ and $\Delta P_d$ are the magnitudes of the corresponding pulsating pressures. Term $P_s+\Delta P_s$ is defined as the simulated dynamic pressure envelop at the spiral case, and term $P_d-\Delta P_d$ is defined as the simulated dynamic pressure envelop at the draft tube.

Using Equation (11) as the objective function, the optimized GVCS and BVCS may not be sufficiently robust or suitable for other scenarios. To address this issue and increase the applicability of the optimized results, multiple scenarios can be considered simultaneously during the optimization process. Therefore, another objective function incorporating multiple scenarios is defined as

$$MinOb{j}_2={\displaystyle \sum }_{i=1}^N{\omega }_i·{\left[max\left\{P_s+\Delta P_s\right\}-min\left\{P_d-\Delta P_d\right\}\right]}_i$$

(12)

where the subscript $i$ represents the parameters for scenario $i$, N is the total number of scenarios, and ${\mathsf{\omega }}_i$ is the weighting coefficient that can be varied for different PSPs. Therefore, the user can choose different weights according to the security level of different scenarios.

Pulsating pressure is a major consideration for turbine manufacturers. Thus, optimization of water hammer pressures and pulsating pressures need to be sometimes separated. Typically, pulsating pressure is greatest at the vaneless space, and that in the draft tube can cause cavitation and affect the operational stability of the pump turbine. Because the peak-to-peak pulsating pressure diagram at the vaneless space is not available, the pulsating pressure at the spiral case, which is mostly propagated from the vaneless space, is used instead to assess the detrimental effects on the turbine. Thus, the other two objective functions can be defined as

$$MinOb{j}_3={\displaystyle \sum }_{i=1}^N{\phi }_i·{\left[max\left\{P_s\right\}-min\left\{P_d\right\}\right]}_i$$

(13)

$$MinOb{j}_4={\displaystyle \sum }_{i=1}^N{\mu }_i·{\left[max\left\{\Delta P_s\right\}+max\left\{\Delta P_d\right\}\right]}_i$$

(14)

where ${\phi }_i$ and ${\mu }_i$ are weighting coefficients.

3.3. Constraints

Multiple constraints are considered in the optimization process, to accelerate the convergence and to improve the search efficiency.

(1) Limit of the closing rate

The relative closing rates of guide vanes and ball valves can be illustrated as Equation (15).

$$\hspace{1em}\{\begin{array}{c}0\le k_G\le k_{G,max}\\ 0\le k_B\le k_{B,max}\end{array}$$

(15)

In Equation (15), $k_G$ and $k_B$ are the closing rates of guide vanes and ball valves, respectively, and $k_{G,max}$ and $k_{B,max}$ represent the maximum limits of the two kinds of closing rates.

(2) Limit of closing time

In the actual load-rejection process, the total closing time of the guide vanes is limited to a range that can be described as

$$T_{G,min}\le T_G\le T_{G,max}$$

(16)

where $T_G$ is the total closing time of the guide vanes, and $T_{G,min}$ and $T_{G,max}$ are the minimum and maximum closing times of the guide vanes, respectively.

The closing time of the ball valve is longer than that of the guide vanes, and thus

$$T_G\le T_B\le T_{B,max}$$

(17)

where $T_B$ is the total closing time of the ball valve and $T_{B,max}$ is the corresponding maximum closing time.

(3) Limit of transient pressures at the spiral case and ball valve

The simulated transient pressure at the spiral case should be limited to a certain level in order to meet the PSP design requirements. Considering the simulation error, a 10% margin for pressure rise is considered, and the constraint on pressure rise is defined as

$$\hspace{1em}\{\begin{array}{c}{P}_{s\_c}= max\left\{P_s+\Delta P_s\right\}+ max\left\{P_s-P_{s,0}\right\}\times 10\%\\ P_{s\_c}\le P_{s\_c,max}\end{array}$$

(18)

where $P_{s,0}$ is the initial pressure at the spiral case and $P_{s\_c, max}$ is the maximum transient pressure allowed at the spiral case.

BVCS might take the risks of displacement and shortened service life of the ball valve in a real system because of the pressure differences between inlet and outlet. Therefore, the inlet pressure of the ball valve should also be monitored [28]. The inlet pressure constraint of the ball valve is set to be the same as that of the spiral case.

(4) Limit of transient pressure at the draft tube

Similar to the pressure constraint at the spiral case, the constraint of transient pressure at the draft tube is set as

$$\{\begin{array}{c}{P}_{d\_c}=min\left\{P_d-\Delta P_d\right\}-min\left\{P_d-P_{d,0}\right\}\times 10\%\\ P_{d\_c}\ge P_{d\_c,min}\end{array}$$

(19)

where $P_{d,0}$ is the initial pressure at the draft tube and $P_{d\_c,min}$ is the minimum transient pressure allowed at the draft tube.

(5) Constraints on the water level in surge tanks

The water levels in a surge tank are constrained as

$$H_{st,min}\le H_{st}\le H_{st,max}$$

(20)

where $H_{st}$ is the water level present in the surge tank, and $H_{st,min}$ and $H_{st,max}$ are the minimum and maximum allowable water levels in the surge tank.

(6) Limit on the rate of speed rise

The constraint of the rate of speed rise is given by

$$\frac{n_{max}-n_0}{n_0}\times 100\%\le r_{max}$$

(21)

where $n_{max}$ is the maximum rotational speed during the transient process, $n_0$ is the rated rotational speed, and $r_{max}$ is the maximum relative speed rise.

(7) Limit on rotational speed oscillation

The number of rotational speed oscillations $Nu{m}_n$ is constrained as

$$Nu{m}_n \le 3$$

(22)

3.4. Evolutionary Algorithms

(a) Genetic algorithm

GAs are popular in engineering [29]. In a GA, each individual within a population is a feasible solution in the solution space. By simulating the evolution process of organisms, the optimal solution is searched for in the solution space. Compared with other optimization methods, a GA has advantages such as strong adaptability, global optimization, simplicity, and universality. Therefore, GAs were adopted for optimization in this paper.

(b) NSGA-II and fuzzy membership degree method

The process of closing pump turbines is fundamentally a multi-objective optimization problem involving multiple constraints because the water hammer pressure and pulsating pressure are conflicting. The Pareto-based NSGA-II [30], one of the most popular multi-objective evolutionary algorithms, has been used in a wide range of multi-objective problems owing to its simple and efficient non-dominated ranking procedure for yielding different Pareto frontier levels. Thus, it is adopted here to optimize the pump turbine closing operation.

The Pareto frontiers provide a set of optimal solutions, from which the most compatible solution can be selected. The fuzzy membership degree method [13] is applied to make fuzzy evaluations for each solution and can be described for each objective function by

$${\mu }_k=\frac{f_{k,max}-f_k}{f_{k,max}-f_{k,min}}$$

(23)

where $f_k$ is the value of the k^th objective function, with the subscripts $max$ and $min$ indicating the maximum and minimum values of the corresponding objective function, respectively. The best compatible solution is that with the maximum $\mu$, which is defined as

$$\mu =\frac{1}{M}{\displaystyle \sum }_{k=1}^M{\mu }_k$$

(24)

where $M$ is the number of objective functions to be optimized.

4. Results and Discussion

4.1. System Specification of the PSP and Field Tests

The case studies presented here are associated with a real PSP in China, with two pump turbines sharing the same main pipelines as shown in Figure 1. The basic parameters of this PSP are listed in

Table 1. PSP parameters.

Upstream Reservoir Water Level (m)	Downstream Reservoir Water Level (m)	Runner inlet Diameter (m)	Rated Head (m)	Rated Flow (m3/s)	Rated Speed (r/min)	Rated Load (MW)
751.57	223.54	3.86	532.74	62.75	500	300

. Some operational requirements that guarantee the safety of the PSP during load-rejection scenarios are listed in

Table 2. Requirements of the PSP.

Index	Requirement
Maximum pressure at the spiral case	820 m
Minimum pressure at the draft tube	12.0 m
Maximum relative speed rise	45%
Maximum water level of the upstream surge tank	770.00 m
Minimum water level of the upstream surge tank	700.00 m
Maximum water level of the downstream surge tank	245.00 m
Minimum water level of the downstream surge tank	180.00 m

.

A field test of load rejection for a single pump turbine was conducted by the turbine manufacturer. The flow was regulated by both guide vanes and the ball valve, with the GVCS and BVCS shown in Figure 8. The load rejection transient process began at 2.96 s. After a short delay, the guide vanes were stalled for approximately 2.98 s, and then fully closed at t = 30.09 s. The ball valve was closed with the closing speed changed at t = 37.65 s.

The same load rejection process was carried out using the proposed model in this paper. The characteristic curves of the pump turbine are shown in Figure 3. The peak-to-peak pulsating pressure diagrams from model tests are shown in Figure 5. The measured and simulated rotational speeds are shown in Figure 9. The measured pressures are shown in Figure 10. It is important to note that the black lines in Figure 10 are the measured total pressure, whereas the red lines are the simulated total pressure envelopes, comprised of the simulated water hammer pressure (in blue lines) and the magnitude of the estimated pulsating pressure.

It can be seen from Figure 9 and Figure 10 that the predicted results are in good agreement with the field data. During the first 8 seconds, the predicted rotational speed first increased and reached its maximum value of 129%, nearly 1 second ahead of the occurring time of the measured maximum of 132%. Then, it dropped sharply. At ~18 s, the rotational speed reached its second maximum of 109%, which was the same as the measured data. The predicted and measured pressures at the spiral case showed a similar tendency with the rotational speed change while the pressure trace at the draft tube appeared inversely as expected. The extremums of the measured and predicted total pressures at the spiral case are 739.1 m and 734.3 m. The extremums of the measured and predicted total pressure at the draft tube are 49.1 m and 51.6 m. To better present the comparison, the measured and predicted extremums and absolute errors are listed in

Table 3. Comparison between measured and predicted results in single load rejection.

	Maximum Relative Rotational Speed	Maximum Total Pressure at the Spiral Case (m)	Minimum Total Pressure at the Draft Tube (m)
Measured	132%	739.1	49.1
Predicted	129%	733.3	51.6
Absolute error	3%	5.8	2.5

.

Considering the errors in the characteristic curves between the real and model pump turbines, together with uncertainties in the field tests and some other error sources, it can be concluded that the numerical model achieves good accuracy in simulating water hammer pressure, and is capable of predicting the changing trend in pulsating pressures during load-rejection scenarios.

In the following sections, three optimization cases are discussed. In Case 1 (single-objective optimization), the guide vanes of one pump turbine are closed in either two or three stages, and the other pump turbine is always closed (the scenario is defined as a single load-rejection scenario). Case 2 (single-objective optimization) considers two load-rejection scenarios: the single load-rejection scenario and the simultaneous load-rejection of two pump turbines. In Case 3, multi-objective optimization of two load-rejection scenarios was conducted by separating the water hammer pressure and the pulsating pressure in the objective functions.

4.2. Case 1: Single-Objective Optimization of Single Load Rejection Scenario

The load rejection start time was set at 0 s. The total closing times of the guide vanes and the ball valve were set to 26 s and 35 s, respectively, which are consistent with the field tests. These settings are consistent in all of the following cases. Other optimization constraints are described in the previous section and Table 2. The GA parameters were set as follows; $Gmax=300$, $np=40$, $pc=0.7$, $pm=0.1$, $mu=0.2$, where $Gmax$ is the total generation, $np$ is the population size, $pc$ is the probability of crossover, $pm$ is the probability of mutation, and $mu$ is the percentage of genetic mutation. The objective function is defined in Equation (11).

Four subcases (Cases 1.1–1.4) in

Table 4. Subcases of single-objective optimization of single load-rejection scenario

Subcases	GVCS	BVCS
Subcase 1.1	Two-stage	Not closed
Subcase 1.2	Three-stage	Not closed
Subcase 1.3	Two-stage	Two-stage
Subcase 1.4	Three-stage	Two-stage

are considered in this section. By running the optimization model, the variations in the objection function across multiple iterations were obtained, as shown in Figure 11; the optimized closing schemes are shown in Figure 12.

It can be seen in Figure 12 that the optimized GVCSs are similar to the theoretical schemes derived in [11]. Comparing cases 1.1 and 1.2 in Figure 13 and Figure 14, respectively, the three-stage closing scheme leads to better performance in terms of both transient pressure and rotational speed. The pressure traces at the spiral case show two peaks for both cases, and increasing the number of closing stages from two to three markedly reduces the first pressure peak when comparing Case 1.1 with Case 1.2 or Case 1.3 with Case 1.4.

4.3. Case 2: Single-Objective Optimization of Two Load Rejection Scenarios

In Case 2, multiple load-rejection scenarios were taken into the single-objective optimization to find a robust closing scheme. The first scenario (Scenario 1) was a single load rejection scenario, and the other (Scenario 2) scenario was a simultaneous full load rejection of two units.

Scenarios 1 and 2 shared a common three-stage GVCS with BVCS in this case. The constraints and setting parameters matched those in Case 1.4. The objective function $Ob{j}_2$ with N = 2 (in Equation (12)) was used for the optimization. In a real PSP system, Scenario 2 is more hazardous than Scenario 1. Thus, a larger weighting factor ${\omega }_2$ was assigned to 0.7, which means giving more emphasis on Scenario 2. The weighting factor ${\omega }_1$ for Scenario 1 was correspondingly assigned to 0.3.

The optimized three-stage GVCS with BVCS is shown in Figure 15, and the dynamic pressure envelopes of the two scenarios are shown in Figure 16. Because the pipeline system is symmetrical with two identical units, only the transient pressure in Unit 2 is presented in Scenario 2 in Figure 16. By comparing the optimized closing schemes with those in Case 1.4, it was found that the optimized GVCS has the same pattern and slightly different turning positions. Thus, such “closing-stall-closing” GVCS is robust for different load-rejection scenarios.

4.4. Case 3: Multi-Objective Optimization of Two Load Rejection Scenarios

In this case, the objective function $Ob{j}_3$ for water hammer pressures and objective function $Ob{j}_4$ for pulsating pressures were optimized simultaneously in NSGA-II. The same two scenarios and weighting factors that used in Case 2 were considered in $Ob{j}_3$ and $Ob{j}_4$. As NSGA-II is a multi-objective optimization genetic algorithm, the control parameters are mostly the same as those of the GA in Case 1. However, a larger population size was used (np = 50) in order to maintain the diversity of solutions as far as possible.

Two subcases were considered in the optimization with (1) guide vanes closed in two stages (Case 3.1) or three stages (Case 3.2), and (2) ball valves closed for both cases.

By running the optimization model, the Pareto front plots were obtained as shown in Figure 17, and the fuzzy membership degree of each Pareto solution was then calculated using Equations (23) and (24). The objective function values as well as the $\mu$ values of partial Pareto-optimal sets are partially given in

Table 5. Partial Pareto optimal solutions by different closing operations.

Scheme	Two-Stage			Three-Stage
	$\mathit{O}\mathit{b}{\mathit{j}}_3\left(\mathbf{m}\right)$	$\mathit{O}\mathit{b}{\mathit{j}}_4\left(\mathbf{m}\right)$	$\mathit{\mu }$	$\mathit{O}\mathit{b}{\mathit{j}}_3\left(\mathbf{m}\right)$	$\mathit{O}\mathit{b}{\mathit{j}}_4\left(\mathbf{m}\right)$	$\mathit{\mu }$
1	630.3	99.7	0.5	625.7	91.5	0.5000
3	641.9	97.8	0.4928	632.4	90.8	0.4975
5	657.7	96.0	0.4667	641.9	89.4	0.5015
7	668.1	95.1	0.4438	647.9	88.8	0.4969
9	672.2	93.9	0.4528	663.1	87.4	0.4835
11	675.9	88.4	0.5452	663.4	87.4	0.4829
13	683.1	86.6	0.5516	664.0	87.3	0.4823
15	685.3	86.3	0.5495	664.1	87.3	0.4824
17	688.8	85.7	0.5482	669.2	86.7	0.4810
19	691.2	85.1	0.5500	669.3	86.7	0.4809
21	691.8	85.0	0.5507	670.0	86.6	0.4804
23	692.1	84.8	0.5525	670.2	86.6	0.4812
25	692.6	84.7	0.5530	670.8	86.5	0.4815
27	693.2	84.5	0.5547	674.1	86.2	0.4785
29	695.9	84.0	0.5532	678.8	85.5	0.4819
31	697.0	83.8	0.5525	685.7	84.2	0.4921
33	698.6	83.6	0.5513	696.5	81.8	0.5221
35	703.8	82.3	0.5558	699.0	81.0	0.5367
37	708.6	81.2	0.5588	703.7	79.8	0.5518
39	712.7	80.1	0.5650	710.7	78.0	0.5787
41	719.2	78.1	0.5784	714.7	76.5	0.6060
43	725.8	76.7	0.5822	720.3	75.2	0.6211
44	728.7	75.3	0.5970	725.7	74.8	0.6140
46	735.8	74.3	0.5902	736.3	74.0	0.5987
48	749.1	74.3	0.5388	758.9	73.5	0.5353
50	760.0	74.1	0.5000	769.4	73.4	0.5000

.

Finally, Scheme 44 in Case 3.1 and Scheme 43 in Case 3.2, which have the maximum value of $\mu$, were selected out for the analysis. The optimized closing schemes are shown in Figure 18.

Figure 17 shows that the selected schemes give more emphasis on reducing the pulsating pressures. Thus, similar GVCSs are obtained for the first 5 s, in which the water hammer pressures increase to their maximum. The GVCSs after 5 s do not affect the maximum transient pressures, as shown in Figure 19 and Figure 20, and thus the two-stage closing scheme is sufficient to achieve adequate results. If the water hammer pressures are assigned a higher priority in the design process, then the weighting factors ${\phi }_1$ and ${\phi }_2$ in Equation (13) can be increased.

5. Conclusions

In this paper, a transient model of load rejection was developed to simulate water hammer pressures and to estimate pulsating pressures in pump turbines. The numerical model was validated by field tests and was then combined with evolutionary algorithms to optimize the pump turbine closing operations (i.e., GVCS and BVCS). By conducting three optimization cases, robust, reliable, and adaptable pump turbine closing operations were obtained for different engineering requirements.

The optimized results have indicated that (1) pressure factors in the pump turbine can be reduced by using GA (for total dynamic pressures) and NSGA-II (for water hammer and pulsating pressures), (2) the three-stage GVCSs are more effective in diminishing the first pressure peak seen on total transient pressure traces when compared with two-stage GVCSs, and (3) such “closing-stall-closing” three-stage GVCSs are applicable to multiple load-rejection scenarios. Overall, this work provided new insight for reducing pulsating pressures in PSPs. However, the estimated pulsating pressures in the proposed model may include some deviation due to the error of peak-to-peak diagrams. Further work will be conducted to improve the estimation performance with the assistance of field tests.