An Analytical Solution for Transient Productivity Prediction of Multi-Fractured Horizontal Wells in Tight Gas Reservoirs Considering Nonlinear Porous Flow Mechanisms
Abstract
:1. Introduction
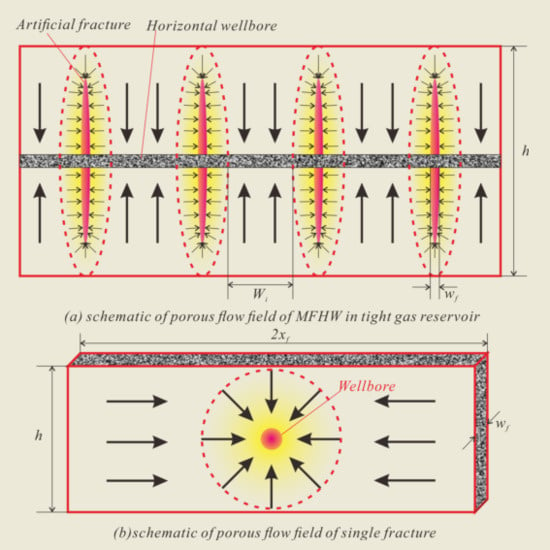
2. Reservoir Characteristics Analysis and Physical Model Assumptions
2.1. Productivity Forecast Model for Individual Horizontal Wells
2.2. Physical Model Assumption
- (1)
- This model is applicable for isothermal single-phase unstable flows and the influence of gravity is neglected.
- (2)
- Fractures completely penetrate the target zone. Fractures and wellbores are arranged both symmetrically and equidistantly, and the fractures are perpendicular to the horizontal wellbore.
- (3)
- Gas flows evenly into fracture along the fracture wall and then into the horizontal wellbore through the fracture.
- (4)
- Mutual interference exists between the fractures and the pressure loss in the wellbore is neglected.
- (5)
- Contamination of the fracture wall is neglected.
- (6)
- Pressure loss in the horizontal wellbore is neglected.
3. Mathematical Model
3.1. Mathematical Model for Nonlinear Flow Mechanisms
3.1.1. Threshold Pressure Gradient Effect
3.1.2. Stress Sensitivity Effect
3.1.3. Gas Slippage Effect
3.2. Productivity Model for Porous Flow between Matrix and Fractures
3.2.1. Steady-state Productivity Model
3.2.2. Transient Model of Discharge Radius in the Matrix
3.2.3. Transient Productivity Model for Fractured Horizontal Wells
3.3. Productivity Model for Porous Flows between the Fracture and Near the Wellbore Area
3.4. Radial Porous Flow Model from Fracture to Wellbore
3.5. Productivity Model of a Single Fracture in Horizontal Wells
3.6. Equivalent Wellbore Radius Model
3.7. Productivity Model of Multi-fractured Horizontal Wells
4. Results and Analysis
4.1. Model Validation
4.2. The Influence of Seepage Mechanisms on Gas Production
4.3. The Influence of Formation Properties on Gas Production
4.4. Influence of Fracture Length on Gas Production
5. Conclusion
- (1)
- The typical production process of fractured horizontal wells in tight gas reservoirs can be divided into three stages based on different seepage areas, flow media, and different seepage characteristics. In the initial stage, the linear and radial flow of gas in fractures shows the tell-tale characteristics of high-speed non-Darcy seepage; in the transitional stage, the gas in the matrix flows in the elliptical seepage area corresponding to each fracture in the near well area; and in the final stage, gas in the matrix flows in the radial seepage area far from the well, both of which show the characteristics of low-speed non-Darcy seepage.
- (2)
- We establish the full cycle productivity prediction model of a multi-stage fractured horizontal well in tight gas reservoirs based on: (a) the different seepage mechanisms of different production stages; and (b) the seepage areas of the horizontal wells in tight gas reservoirs. This is accomplished by considering nonlinear seepage mechanisms, such as the gas slippage effect, threshold pressure gradient, stress sensitive effect, and the confluence of multiple interferences within these fractures.
- (3)
- Based on the actual gas field data, we compared and analyzed the productivity prediction model established in this study using CMG. The results obtained by the two methods have an error of less than 1.62%. We demonstrated that the proposed model is accurate enough to simulate production of a multi-stage fractured horizontal well in a tight gas reservoir.
- (4)
- The significance of four influencing parameters to contribution degree of productivity was analyzed. Except for the seepage effect, the three other factors, namely turbulence effect, stress sensitivity, and threshold pressure gradient effect, have a negative effect on productivity. The increasing influence of contribution factors of production is as follows: threshold pressure gradient, stress sensitivity, turbulence effect, and slippage effect. At the end of production, each contribution degree of these parameters is −29.3%, −15.2%, −5.4%, and 4.8%.
- (5)
- According to the model proposed in this study, the sensitivity analysis of the productivity of fractured horizontal wells was carried out by employing the characteristics of seepage mechanisms, reservoir physical properties, and techniques. Different parameters have different effects on the initial production, stable production, stable production span, and final production of gas wells. These factors need to be comprehensively considered while optimizing any future gas field plan.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ma, Y.; Cai, X.; Zhao, P. China’s shale gas exploration and development: Understanding and practice. Pet. Explor. Dev. 2018, 45, 589–603. [Google Scholar] [CrossRef]
- Zhiming, C.; Xinwei, L.; Chenghui, H.; Xiaoliang, Z.; Langtao, Z.; Yizhou, C.; Heng, Y.; Zhenhua, C. Productivity estimations for vertically fractured wells with asymmetrical multiple fractures. J. Nat. Gas Sci. Eng. 2014, 21, 1048–1060. [Google Scholar] [CrossRef]
- Wang, W.; Fan, D.; Sheng, G.; Chen, Z.; Su, Y. A review of analytical and semi-analytical fluid flow models for ultra-tight hydrocarbon reservoirs. Fuel 2019, 256, 115737. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, L.; Luo, J.; Zhang, B. Performance of fractured horizontal well with stimulated reservoir volume in unconventional gas reservoir. J. Hydrol. 2014, 512, 447–456. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Z.; Yao, J.; Zhang, L.; Ma, J.; Hejazi, S.; Luquot, L.; Ngarta, T. Flow simulation of artificially induced microfractures using digital rock and lattice Boltzmann methods. Energies 2018, 11, 2145. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Yao, J.; Wang, C.; Gao, Y.; Zhang, Q.; An, S.; Song, W. New pore space characterization method of shale matrix formation by considering organic and inorganic pores. J. Nat. Gas Sci. Eng. 2015, 27, 496–503. [Google Scholar] [CrossRef]
- Qiang, W.; Min, T.; Zhanguo, W.; Yi, W. An Unsteady Productivity Prediction Method of Multi-fractured Horizontal Well in Tight Volcanic Rock Reservoir. J. Southwest Pet. Univ. (Sci. Technol. Ed.) 2014, 36, 107–115. [Google Scholar]
- Zou, C.; Zhu, R.; Wu, S.; Yang, Z.; Tao, S.; Yuan, X. Types, characteristics, genesis and prospects of conventional and unconventional hydrocarbon accumulations:taking tight oil and tight gas in China as an instance. Acta Pet. Sin. 2012, 33, 173–187. [Google Scholar]
- Zhao, J.; Pu, X.; Li, Y.; He, X. A semi-analytical mathematical model for predicting well performance of a multistage hydraulically fractured horizontal well in naturally fractured tight sandstone gas reservoir. J. Nat. Gas Sci. Eng. 2016, 32, 273–291. [Google Scholar] [CrossRef]
- Wang, Z.; Ran, B.; Tong, M.; Wang, C.; Yue, Q. Forecast of fractured horizontal well productivity in dual permeability layers in volcanic gas reservoirs. Pet. Explor. Dev. 2014, 41, 642–647. [Google Scholar] [CrossRef]
- Sun, H.; Ouyang, W.; Zhang, M.; Tang, H.; Chen, C.; Ma, X.; Fu, Z. Advanced production decline analysis of tight gas wells with variable fracture conductivity. Pet. Explor. Dev. 2018, 45, 472–480. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, W.; Gao, Y.; Wan, Y.; Su, Y.; An, S.; Sun, H.; Zhang, L.; Zhao, J.; Liu, L.; et al. Influence of stress sensitivity on microscopic pore structure and fluid flow in porous media. J. Nat. Gas Sci. Eng. 2016, 36, 20–31. [Google Scholar] [CrossRef]
- Wan, J.; Peng, T.; Shen, R.; Jurado, M.J. Numerical model and program development of TWH salt cavern construction for UGS. J. Pet. Sci. Eng. 2019, 179, 930–940. [Google Scholar] [CrossRef] [Green Version]
- Bagher Asadi, M.; Dejam, M.; Zendehboudi, S. Semi-Analytical Solution for Productivity Evaluation of a Multi-Fractured Horizontal Well in a Bounded Dual-Porosity Reservoir. J. Hydrol. 2019, 124288. [Google Scholar]
- Dong, J.; Chen, M.; Jin, Y.; Hong, G.; Zaman, M.; Li, Y. Study on micro-scale properties of cohesive zone in shale. Int. J. Solids Struct. 2019, 163, 178–193. [Google Scholar] [CrossRef]
- Qiang, W.; Mengni, Y.; Ning, L.; Yufeng, Y.; Jiaxin, D. Research progress of numerical simulation models for shale gas reservoirs. Geol. China 2019, 46, 1284–1299. [Google Scholar]
- Xiao, C.; Meng, Z.; Tian, L. Semi-analytical modeling of productivity analysis for five-spot well pattern scheme in methane hydrocarbon reservoirs. Int. J. Hydrog. Energy 2019, 44, 26955–26969. [Google Scholar] [CrossRef]
- Luo, W.; Tang, C.; Zhou, Y.; Ning, B.; Cai, J. A new semi-analytical method for calculating well productivity near discrete fractures. J. Nat. Gas Sci. Eng. 2018, 57, 216–223. [Google Scholar] [CrossRef]
- Sun, Z.; Shi, J.; Zhang, T.; Wu, K.; Feng, D.; Sun, F.; Huang, L.; Hou, C.; Li, X. A fully-coupled semi-analytical model for effective gas/water phase permeability during coal-bed methane production. Fuel 2018, 223, 44–52. [Google Scholar] [CrossRef]
- Zhang, Z.; Ayala H, L.F. Analytical dual-porosity gas model for reserve evaluation of naturally fractured gas reservoirs using a density-based approach. J. Nat. Gas Sci. Eng. 2018, 59, 224–236. [Google Scholar] [CrossRef]
- Tian, F.; Wang, X.; Xu, W. A semi-analytical model for multiple-fractured horizontal wells in heterogeneous gas reservoirs. J. Pet. Sci. Eng. 2019, 183, 106369. [Google Scholar] [CrossRef]
- Zeng, J.; Li, W.; Liu, J.; Leong, Y.-K.; Elsworth, D.; Tian, J.; Guo, J.; Zeng, F. Analytical solutions for multi-stage fractured shale gas reservoirs with damaged fractures and stimulated reservoir volumes. J. Pet. Sci. Eng. 2019, 106686. [Google Scholar] [CrossRef]
- Berawala, D.S.; Andersen, P.Ø.; Ursin, J.R. Controlling Parameters During Continuum Flow in Shale-Gas Production: A Fracture/Matrix-Modeling Approach. SPE-190843-PA 2019, 24, 1378–1394. [Google Scholar] [CrossRef]
- Ren, W.; Lau, H.C. Analytical modeling and probabilistic evaluation of gas production from a hydraulically fractured shale reservoir using a quad-linear flow model. J. Pet. Sci. Eng. 2020, 184, 106516. [Google Scholar] [CrossRef]
- Garra, R.; Salusti, E. Application of the nonlocal Darcy law to the propagation of nonlinear thermoelastic waves in fluid saturated porous media. Phys. D Nonlinear Phenom. 2013, 250, 52–57. [Google Scholar] [CrossRef]
- Balankin, A.S.; Valdivia, J.-C.; Marquez, J.; Susarrey, O.; Solorio-Avila, M.A. Anomalous diffusion of fluid momentum and Darcy-like law for laminar flow in media with fractal porosity. Phys. Lett. A 2016, 380, 2767–2773. [Google Scholar] [CrossRef]
- Hao, F.; Cheng, L.S.; Hassan, O.; Hou, J.; Liu, C.Z.; Feng, J.D. Threshold Pressure Gradient in Ultra-low Permeability Reservoirs. Pet. Sci. Technol. 2008, 26, 1024–1035. [Google Scholar] [CrossRef]
- Zeng, F.; Peng, F.; Guo, J.; Xiang, J.; Wang, Q.; Zhen, J. A Transient Productivity Model of Fractured Wells in Shale Reservoirs Based on the Succession Pseudo-Steady State Method. Energies 2018, 11, 2335. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Su, Y.; Yuan, B.; Wang, K.; Cao, X. Numerical Simulation of Fluid Flow through Fractal-Based Discrete Fractured Network. Energies 2018, 11, 286. [Google Scholar] [CrossRef] [Green Version]
- Soliman, M.Y.; Hunt, J.L.; Azari, M. Fracturing Horizontal Wells in Gas Reservoirs. Spe Prod. Facil. 1999, 14, 277–283. [Google Scholar] [CrossRef]
- Rubin, C.; Zamirian, M.; Takbiri-Borujeni, A.; Gu, M. Investigation of gas slippage effect and matrix compaction effect on shale gas production evaluation and hydraulic fracturing design based on experiment and reservoir simulation. Fuel 2019, 241, 12–24. [Google Scholar] [CrossRef]
- Zhao, T.; Zhao, H.; Ning, Z.; Li, X.; Wang, Q. Permeability prediction of numerical reconstructed multiscale tight porous media using the representative elementary volume scale lattice Boltzmann method. Int. J. Heat Mass Transf. 2018, 118, 368–377. [Google Scholar] [CrossRef]
- Cao, P.; Liu, J.; Leong, Y.-K. Combined impact of flow regimes and effective stress on the evolution of shale apparent permeability. J. Unconv. Oil Gas Resour. 2016, 14, 32–43. [Google Scholar] [CrossRef]
- Li, J.; Sultan, A.S. Klinkenberg slippage effect in the permeability computations of shale gas by the pore-scale simulations. J. Nat. Gas Sci. Eng. 2017, 48, 197–202. [Google Scholar] [CrossRef] [Green Version]
- Firouzi, M.; Alnoaimi, K.; Kovscek, A.; Wilcox, J. Klinkenberg effect on predicting and measuring helium permeability in gas shales. Int. J. Coal Geol. 2014, 123, 62–68. [Google Scholar] [CrossRef]
- Liu, Y.-W.; Liu, C.-Q. New Analysis Method for the Vertical Fracture Well. In International Meeting on Petroleum Engineering; Society of Petroleum Engineers: Beijing, China, 1995; p. 10. [Google Scholar]
- Ren, Z.; Yan, R.; Huang, X.; Liu, W.; Yuan, S.; Xu, J.; Jiang, H.; Zhang, J.; Yan, R.; Qu, Z. The transient pressure behavior model of multiple horizontal wells with complex fracture networks in tight oil reservoir. J. Pet. Sci. Eng. 2019, 173, 650–665. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, L.; Xiong, Y.; Zhou, Y.; Liu, Q.; Chen, D. Pressure response and production performance for multi-fractured horizontal wells with complex seepage mechanism in box-shaped shale gas reservoir. J. Nat. Gas Sci. Eng. 2016, 32, 66–80. [Google Scholar] [CrossRef]
- Zhu, W.; Qi, Q.; Ma, Q.; Deng, J.; Yue, M.; Liu, Y. Unstable seepage modeling and pressure propagation of shale gas reservoirs. Pet. Explor. Dev. 2016, 43, 285–292. [Google Scholar] [CrossRef]
- Feng, Z.; ShiMin, D.; JianMin, Q.; SiQing, D.; WeiGang, S.; JiGui, Y. Productivity of the Horizontal Well with Finite-conductivity Fractures. Nat. Gas Geosci. 2009, 20, 817–821. [Google Scholar]
- Lamarche, L. Short-time analysis of vertical boreholes, new analytic solutions and choice of equivalent radius. Int. J. Heat Mass Transf. 2015, 91, 800–807. [Google Scholar] [CrossRef]
- Mbia, E.N.; Fabricius, I.L.; Oji, C.O. Equivalent pore radius and velocity of elastic waves in shale. Skjold Flank-1 Well, Danish North Sea. J. Pet. Sci. Eng. 2013, 109, 280–290. [Google Scholar] [CrossRef]
















| Parameters (Unit) | Value |
|---|---|
| Initial formation pressure () | 52 |
| Bottom hole flow pressure () | 44 |
| Porosity (-) | 0.06 |
| Initial permeability of matrix () | 0.4 |
| Initial permeability of fracture () | 5000 |
| Viscosity () | 0.8 |
| z-factor (-) | 1.2 |
| Thickness of formation (m) | 15 |
| Horizontal length (m) | 850 |
| Width of fracture (m) | 0.003 |
| Spacing of fracture (m) | 80 |
| Molecular mass () | 17.28 |
| Comprehensive compression coefficient of formation () | 0.0023 |
| Stress sensitivity coefficient of matrix () | 0.3 |
| Stress sensitivity coefficient of fracture () | 0.3 |
| Gas slippage factor () | 2 |
| Reservoir temperature () | 293 |
| Borehole radius (m) | 0.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Wan, J.; Mu, L.; Shen, R.; Jurado, M.J.; Ye, Y. An Analytical Solution for Transient Productivity Prediction of Multi-Fractured Horizontal Wells in Tight Gas Reservoirs Considering Nonlinear Porous Flow Mechanisms. Energies 2020, 13, 1066. https://doi.org/10.3390/en13051066
Wang Q, Wan J, Mu L, Shen R, Jurado MJ, Ye Y. An Analytical Solution for Transient Productivity Prediction of Multi-Fractured Horizontal Wells in Tight Gas Reservoirs Considering Nonlinear Porous Flow Mechanisms. Energies. 2020; 13(5):1066. https://doi.org/10.3390/en13051066
Chicago/Turabian StyleWang, Qiang, Jifang Wan, Langfeng Mu, Ruichen Shen, Maria Jose Jurado, and Yufeng Ye. 2020. "An Analytical Solution for Transient Productivity Prediction of Multi-Fractured Horizontal Wells in Tight Gas Reservoirs Considering Nonlinear Porous Flow Mechanisms" Energies 13, no. 5: 1066. https://doi.org/10.3390/en13051066
APA StyleWang, Q., Wan, J., Mu, L., Shen, R., Jurado, M. J., & Ye, Y. (2020). An Analytical Solution for Transient Productivity Prediction of Multi-Fractured Horizontal Wells in Tight Gas Reservoirs Considering Nonlinear Porous Flow Mechanisms. Energies, 13(5), 1066. https://doi.org/10.3390/en13051066