Effect of Pore Size Heterogeneity on Hydrocarbon Fluid Distribution, Transport, and Primary and Secondary Recovery in Nano-Porous Media

Abstract

In this paper, we investigate the effect of pore size heterogeneity on fluid composition distribution of multicomponent-multiphase hydrocarbons and its subsequent influence on mass transfer in shale nanopores. The change of multi-contact minimum miscibility pressure (MMP) in heterogeneous nanopores was investigated. We used a compositional simulation model with a modified flash calculation, which considers the effect of large gas–oil capillary pressure on phase behavior. Different average pore sizes for different segments of the computational domain were considered and the effect of the resulting heterogeneity on phase change, composition distributions, and production was investigated. A two-dimensional formulation was considered here for the application of matrix–fracture cross-mass transfer and the rock matrix can also consist of different segments with different average pore sizes. Both convection and molecular diffusion terms were included in the mass balance equations, and different reservoir fluids such as ternary mixture syntactic oil, Bakken oil, and Marcellus shale condensate were considered. The simulation results indicate that oil and gas phase compositions vary in different pore sizes, resulting in a concentration gradient between the two adjacent pores of different sizes. Given that shale permeability is extremely small, we expect the mass transfer between the two sections of the reservoir/core with two distinct average pore sizes to be diffusion-dominated. This observation implies that there can be a selective matrix–fracture component mass transfer as a result of confinement-dependent phase behavior. Therefore, the molecular diffusion term should be always included in the mass transfer equations, for both primary and gas injection enhanced oil recovery (EOR) simulation of heterogeneous shale reservoirs.

1. Introduction

Benefiting from hydraulic fracturing and horizontal drilling, the production of unconventional oil and gas has grown rapidly in the past decades, making a great contribution to hydrocarbon production in North America [1,2].

The pore size in tight rocks is nano-scale, typically 50 nm or even smaller [3]. Due to the nano-scale radius of curvature of the gas/liquid interface, gas–oil capillary pressure can be up to several hundreds of psi, and such large capillary pressure may change the properties of hydrocarbon mixtures, such as phase compositions, density, and viscosity [4,5,6]. Brusilovsky [7] studied the effect of capillary pressure on phase behavior by incorporating the capillary pressure in the phase fugacity equations. The results showed that for hydrocarbon mixtures, the bubble-point pressure decreased, and dew-point pressure increased as the pore size became smaller. Even though he mentioned that such curvatures were unlikely to exist in hydrocarbon reservoirs, recent extensive studies of tight oil resources revealed that such a phenomenon occurred in the confined space. Nojabaei et al. (2013) [5] further investigated the effect of high capillary pressure on the entire P-T phase envelop for binary mixtures and the Bakken fluid. They discovered that, far from the critical point, the shape of phase envelop would change and including the large oil–gas capillary pressure effect in phase behavior calculations resulted in bubble-point pressure reduction, while the dew-point pressure either decreased or increased depending on the pressure. Furthermore, they found that the two-phase oil and gas density and viscosity, as well as the phase compositions, would be altered by including the capillary pressure effect in flash calculations.

Based on another group of previous studies, the phase behavior of hydrocarbon fluid mixture deviated from the original pattern in confined spaces due to the shift of critical properties [8,9]. Studies revealed that the nano-confined physical space could alter the critical pressure and temperatures as well as the phase envelope. Teklu et al. [10] showed that including critical property shifts could significantly change the bubble-point and dew-point pressures of mixtures. However, it is still an open question whether the critical point should change in a confined space, such as a shale matrix. Furthermore, van der Waals force also affects phase behaviors but the contribution of van der Waals forces is smaller compared to capillary pressure [11].

In conventional reservoirs, the transportation of hydrocarbon mixture in porous media is governed by Darcy’s flow. However, in ultra-tight low permeability shales, the pressure gradient and gravitational drainage are inefficient [12,13,14]. In such a condition, molecular diffusion may play an important role in oil recovery and influence mass transport. Numerous computational and experimental research studies have been done to study the effect of diffusion on oil and gas recovery in fractured shale reservoirs. Ghorayeb and Firoozabadi [15] studied the fracture parameters on the fluid compositional distribution. The simulation results revealed that convection took place in high permeability fractures, and the composition gradient was higher for fractures with a larger width. Darvish et al. [16] simulated CO₂ injection in a fractured reservoir and concluded that the main recovery mechanism was diffusion and the contribution of gravity drainage was very small. They also pointed out that cross-phase diffusion was important. Similarly, Hoteit and Firoozabadi [17] also stated that cross-phase diffusion should be considered and based on the theory of crossflow equilibrium. They proposed a method by assuming that gas and liquid phases were in equilibrium at the interface. Moortgat and Firoozabadi [13] indicated the existence of a numerical issue of classical Fick’s model due to the exclusive definition of the compositional gradient within each phase, and they had numerical errors when two neighboring grid cells contained single-phase fluids. This problem often occurs with sharp phase boundaries such as in CO₂ saturated fractures. They proposed an alternative model to evade this problem by replacing the compositional gradient with a chemical potential gradient as the driving force. Simonnin et al. [18] derived analytical expressions to account for the finite-size effects on diffusion in confined fluids. Many other studies [19,20,21,22] also investigated phase behaviors and thermodynamic properties under confinement effects. Given that a dual-porosity model is not appropriate for the simulation of matrix–fracture exchange for a discrete fracture network (DFN), some researchers [23] used an embedded discrete fracture model (EDFM). Elputranto and Akkutlu [24] proposed the capillary-end effect phenomenon. The invaded fracturing water could result in a large gas–water capillary pressure at the fracture-matrix interface and amplify the liquid bock in the formation.

Regarding the importance of minimum miscibility pressure (MMP) in shale and tight rocks, Cronin et al. [25] pointed out that traditional concept of multi-contact minimum miscibility pressure (MCMMP) is based on advection-dominated transport within matrix but not diffusion-dominated mass transfer and in low permeability rocks, only first contact MMP is important. Other studies pointed out that the value of MMP would be affected by the nanopore confinement effect (critical properties shift) in shale [26,27]. Recently, Zhang et al. [28] studied the effect of gas–oil capillary pressure on MMP in tight rocks, where diffusion is still minimal, and concluded that capillary pressure may influence the MCMMP, but such effect was negligible for the cases that were examined.

The effect of nanopore confinement on phase behavior commonly occurs at the nanopore throat of the shale matrix and will alter the composition of oil and gas compared to the bulk region. In this paper, we investigated the effect of pore size heterogeneity on the composition distribution of multicomponent hydrocarbon fluids and its influence on fluid properties, such as density and viscosity. The influence of diffusion on CO₂ MMP within heterogeneous pore size reservoirs is also discussed. We used an open-source and multifunction reservoir simulator (Matlab Reservoir Simulation Toolbox, MRST [29]) and modified the compositional model of this simulator by including the effect of large gas–oil capillary pressure on phase behavior in flash calculations and adding the diffusion term in the mass balance equations. Meanwhile, a core-scale heterogeneous model (using different average pore sizes for different segments of the computational domain) was considered, and its influence on phase and composition distributions and production was investigated. A two-dimensional formulation was considered here to model matrix–fracture cross-mass transfer and both convection and molecular diffusion terms were included in the mass balance equations. The diffusion behavior of three types of reservoir fluids, including a ternary mixture, Bakken oil, and Marcellus condensate in heterogeneous reservoirs was examined.

To estimate MMP of CO₂ and oil in a heterogeneous pore size setup, we use a one-dimensional fully compositional formulation to estimate recoveries.

2. Model and Methodology

The effect of heterogeneous pore-size on fluid transportation and composition distribution was investigated by using a 2-D compositional simulation model, which considers the effect of the large gas–oil capillary pressure in the flash calculation, and diffusion in the mass transport model. We assumed that the equation of states is applicable in nanopores, and the concept of capillary pressure is still valid in such small pores. We also assumed that Fick’s law is valid in nanopores to describe the diffusion behavior, however, to accurately evaluate the applicability of such pragmatic larger-scale concepts and equations depending on the fluid type and pore size, further molecular-scale research is needed.

Here we explain our flash calculation model, the inclusion of diffusion term, and the implementation design of pore size heterogeneity in our calculations.

2.1. Flash Calculation with Large Gas–Oil Capillary Pressure

In the study by Nojabaei et al. [30], oil pressure is the reference pressure and large gas–oil capillary pressure is added to the oil pressure to calculate the gas phase pressure. Considering that there are uncertainties about the choice of the reference pressure, we modified the phase pressures calculations to allow for a reference pressure that can be either equal to the oil (liquid) pressure, equal to the gas (vapor) pressure, or between vapor ($P^V$) and liquid pressure ($P^L$), as shown in the following equations:

$$P^V=P_{ref}+ref\times p_c$$

(1)

$$P^L=P_{ref}-\left(1-ref\right)\times p_c$$

(2)

$$p_c=\frac{2\sigma }{r}$$

(3)

$$f_i^V\left(T,P^V,y_1\cdots y_{Nc}\right)=f_i^L\left(T,P^L,x_1\cdots x_{Nc}\right),i=1-N_C$$

(4)

where $p_c$ is the capillary pressure, $ref$ is the adjusting parameter for the reference pressure, which is between zero and one, and σ is the oil–gas interfacial tension (IFT). The interfacial tension is calculated with the Macleod and Sugden correlation [31]:

$$\sigma ={\left[{\displaystyle \sum }_i^{N_c}{X}_i\left(x_i{\overline{\rho }}^L-y_i{\overline{\rho }}^V\right)\right]}^4$$

(5)

where $X_i$ is the parachor of component $i$, $x_i$ is the molar fraction of component $i$ in the liquid phase, $y_i$ is the molar fraction of component $i$ in the vapor phase, ${\overline{\rho }}^L$ is the mass density of the liquid phase, and ${\overline{\rho }}^V$ is the mass density of the vapor phase.

2.2. Molecular Diffusion Model

For a multicomponent fluid system, the mass conservation for each component is shown as follows

$$\frac{\delta }{\delta t}(\varphi {\displaystyle \sum }_{\alpha }{c}_{\alpha }^i{\rho }_{\alpha }{S}_{\alpha })+\nabla \cdot ({\displaystyle \sum }_{\alpha }{c}_{\alpha }^i{\rho }_{\alpha }{\overrightarrow{v}}_{\alpha }+{\overrightarrow{J}}_{\alpha }^i)={\displaystyle \sum }_{\alpha }{c}_{\alpha }^i{\rho }_{\alpha }{q}_{\alpha }$$

(6)

where ${\overrightarrow{v}}_{\alpha }$ is the overall velocity of phase α, $q_{\alpha }$ is the source term and ${\overrightarrow{J}}_{\alpha }^i$ is the Fickian diffusion flow of phase α. In hydrocarbon mixtures, each phase contains multiple components, and due to Brownian motion, these components redistribute driven by the concentration or mass fraction gradient. In this study, the classic Fickian diffusion model was used to describe the diffusion behavior according to

$${\overrightarrow{J}}_{\alpha }^i=-{\rho }_{\alpha }{S}_{\alpha }{D}_{\alpha }^i\nabla c_{\alpha }^i$$

(7)

where $c_{\alpha }^i$ is the mass fraction of component $i$ in phase $\alpha$, ${\rho }_{\alpha }$ is the mass density of phase $\alpha$, $S_{\alpha }$ is the saturation of phase $\alpha$, $D_{\alpha }^i$ is the diffusion coefficient of component $i$ in phase $\alpha$. To calculate diffusion coefficients of components in oil and gas phases, the commonly used Sigmund correlation (1976a,b) [32,33] is applied:

$$D_{\alpha }^i=\frac{1-c_{\alpha }^i}{{{\displaystyle \sum }}_{i\ne j}\frac{c_{\alpha }^i}{D_{ij}}}$$

(8)

where $D_{ij}$ is the binary diffusion coefficient between component $i$ and $j$, which is calculated by

$$D_{ij}=\frac{{\partial }_{\alpha }^0{D}_{ij}^0}{{\partial }_{\alpha }}\left(0.99589+0.096016{\partial }_{\alpha r}-0.22035{\partial }_{\alpha r}^2+0.032874{\partial }_{\alpha r}^3\right)$$

(9)

where ${\partial }_{\alpha }$ and ${\partial }_{\alpha r}$ are the molar density and the reduced molar density of phase $\alpha$; ${\partial }_{\alpha }^0{D}_{ij}^0$ is the zero measure limit of the product and diffusivity in phase $\alpha$. These factors can be calculated through these functions:

$${\partial }_{\alpha }^0{D}_{ij}^0=\frac{0.0018583T^{1/2}}{{\sigma }_{ij}^2{\Omega }_{ij}R}{\left(\frac{1}{M_i}+\frac{1}{M_j}\right)}^{1/2}$$

(10)

$${\partial }_{\alpha r}={\partial }_{\alpha }\frac{{{\displaystyle \sum }}_{i=1}^{n_c}{c}_{\alpha }^i{v}_{ci}^{5/3}}{{{\displaystyle \sum }}_{i=1}^{n_c}{c}_{\alpha }^i{v}_{ci}^{2/3}}$$

(11)

where $M_i$ is the molar weight of component $i$; ${\sigma }_{ij}$ is the collision diameter; ${\Omega }_{ij}$ is the collision integral of the Lennard–Jones potential, and $v_{ci}$ is the critical volume of component $i$. The parameters of ${\sigma }_{ij}$ and ${\Omega }_{ij}$ are calculated by the following equations:

$${\sigma }_{ij}=\frac{{\sigma }_i+{\sigma }_j}{2}$$

(12)

$${\sigma }_i=\left(2.3551-0.087{\omega }_i\right){\left(\frac{T_{ci}}{P_{ci}}\right)}^{1/3}$$

(13)

$${\epsilon }_i=k_B\left(0.7915+0.1963{\omega }_i\right)T_{ci}$$

(14)

$${\Omega }_{ij}=\frac{1.06036}{T_{ij}^{0.1561}}+\frac{0.193}{exp(0.47635T_{ij})}+\frac{1.03587}{exp(1.52996T_{ij})}+\frac{1.7674}{exp(3.89411T_{ij})}$$

(15)

where ${\omega }_i$ is the acentric factor of component $i$, $P_{ci}$ and $T_{ci}$ are the critical pressure and temperature of component $i$, ${\epsilon }_i$ is the characteristic Lennard–Jones energy (ergs), and $k_B$ is the Boltzmann’s constant. The units of the parameters in the above equations are stated in the nomenclature section.

2.3. Heterogeneous Pore-Size Domain Set Up for Matrix–Fracture Interface

To investigate the effect of heterogeneous pore size distribution on fluid properties in fractured reservoirs, we set up a 2D simulation domain with 10 m in length ($y$), and 3 mm in width ($x$) as shown in Figure 1. The fracture (x = 0) refers to the hydraulic fracture with larger pores, and the matrix (x = 3 mm) refers to the porous media with nano-scale pores. The half-length of the hydraulic fracture is 10 m. The pore size is assumed to decrease along the transition zone (from the fracture to the matrix, i.e., 0 < x < 3 mm). Considering that pore-size only changes in the x-direction and there is no production well in the simulation domain, there is no viscous flow or mass transfer in the other directions.

The pore size ($r$) changes along $x$ direction, from 10,000 nm (bulk region) to 10 nm (nanopore region) and the pore size changes with $x$ based on the following function.

$$r=\frac{{10}^{-5}}{\left(\frac{1-\cos \left(\frac{x}{3}\pi \right)}{2}+0.001\right)}$$

(16)

The distribution of pore size and initial capillary pressure along the x-direction for different fluids is shown in Figure 2. Here in our simulation, as x varies from 0 to 3 mm, the pore size ($r$) decreases from 0.01 mm (= 10000 nm) to 0.00001 mm (= 10 nm). Owing to that the pore-size variation that only occurs in the x-direction and considering that no production well exists in the reservoir domain, there is no viscous flow or mass transfer in the y-direction. The flow in the x-direction is driven by the capillary pressure-induced pressure gradient as well as the concentration gradient-induced molecular diffusion.

2.4. Slim Tube Simulation

Minimum miscibility pressure (MMP) is a key design parameter for gas injection. We used slim tube simulations to investigate the influence of molecular diffusion and heterogeneous pore size on MMP. Slim tube experiments are the most common method used to estimate multi-contact MMP. In this experiment, injection gas displaces oil in a slim tube and oil recovery factors were recorded after 1.2 pore volume of gas was injected. The oil recovery curve was plotted against pressure and the bend of this curve indicates MMP. Slim tube simulation is a numerical method to simulate the slim-tube experiment and we implemented this simulation with MATLAB Reservoir Simulation Toolbox (MRST). Here we implemented a heterogeneous pore size reservoir in the simulation, and the pore size distribution is shown in Figure 3.

3. Results

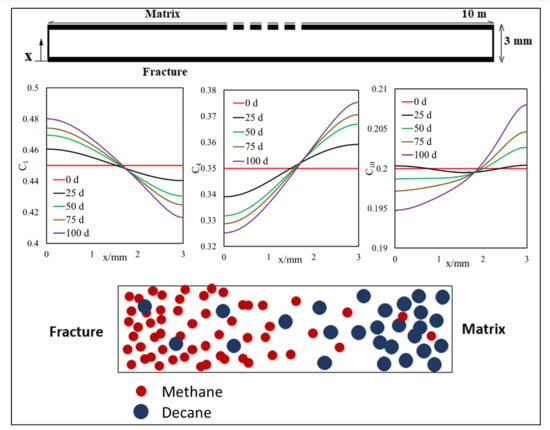
3.1. Matrix–Fracture System

Nanopores alter the phase behavior of multiphase multicomponent hydrocarbon mixtures, owing to the large gas–oil capillary pressure. For heterogeneous porous media, phase compositions are different in pores with different sizes, which would lead to a compositional gradient. As shown in Figure 4, for a case without any source or sink term (e.g., no production or injection pressure different from the reservoir pressure), the capillary pressure term in the mass balance equations provides a pressure gradient for Darcy’s flow, and diffusion is driven by compositional gradient which is the result of the effect of inclusion of capillary pressure on phase equilibrium calculations.

In this section, we investigate the effect of molecular diffusion on the phase composition changes within a 2-D fracture-matrix set up for three different types of fluids, i.e., a simple ternary mixture, Bakken shale oil, and Marcellus shale condensate. We used the ternary mixture to examine the effect of capillary pressure on viscous flow and discuss the effect of using different reference pressures. In the last section, we combine both molecular diffusion and capillary pressure in flow and examine this combined effect on compositional profile and fluid properties.

3.1.1. Effect of Diffusion on Mass Transfer

To study the effect of heterogeneous pore size on molecular diffusion and its subsequent influence, we start with a ternary mixture with an overall composition of 45% C₁, 35% C₄, and 20% C₁₀. The original mixture is in two phases at the given temperature of 160 °F and pressure of 1200 psia. Note that there is no pressure gradient introduced to the system. The size and properties of the 2D fracture–matrix domain are shown in

Table 1. Properties of the fracture–matrix 2D setup.

Cell Numbers	400 × 10
Size of the system/m	0.003 × 10
Initial pressure/psia	1200
Pore size/nm	As shown in Figure 3
Porosity	0.06
Permeability/nd	0.1

. Here we set large pore sizes for the fracture and very small pores for the matrix, and we use only one value for permeability to exclude the other effects that might be connected to heterogeneous permeability. As shown in Figure 3, the pore size changes along the x-direction from 10,000 to 10 nm. The fluid properties and binary interaction parameters are given in

Table 2. Compositional data for the C₁/C₄/C₁₀ system.

Component	Critical Pressure (psia)	Critical Temperature (R)	Acentric Factor	Molecular Weight (lbm/lb mol)	Parachor
C1	667.2	343.08	0.008	16.043	74.8
C4	551.1	765.36	0.193	58.124	189.6
C10	353.76	1070.831	0.5764	134	372.86

and

Table 3. Binary interaction parameters for the C₁/C₄/C₁₀ system.

Component	C1	C4	C10
C1	0	0.119	0.008
C4	0.119	0	0.0847
C10	0.008	0.0847	0

. In the simulation model, $ref=1$ is used to calculate the phase pressure and the liquid pressure is the reference pressure here. The initial phase composition is altered due to the effect of capillary pressure, as shown in Figure 5.

It should be noted that here capillary pressure in flow is excluded, and as a result, Darcy flow does not contribute to fluid transport because the pressure gradient is zero. Mass transfer is only driven by molecular diffusion caused by the inclusion of the capillary pressure effect in the phase behavior model. Owing to the large capillary pressure in flash, the phase composition of each component varies at different pore radius (Figure 5) and changes with diffusion over time, as plotted in Figure 6. The red horizontal line in Figure 6 represents the initial overall composition. As time goes by, the concentration of the light component (C₁) decreases in the matrix (x > 1.5 mm) but increases in the fracture domain (x < 1.5 mm) and the concentration difference between them is about 6%. Intermediate components (C₄ and C₁₀) move from the fracture to the tight matrix and the concentration difference is about 5% and 1.5%, respectively.

The large oil-gas capillary pressure not only influences the composition distribution but also alters the phase properties, such as density and viscosity. In Figure 7, the initial viscosities and densities of oil and gas vary at different locations with different pore sizes. Driven by molecular diffusion, the densities of oil in fracture and gas in matrix increase while the densities of oil in matrix and gas in fracture decrease and viscosities have a similar trend. Our results show that as time passes, the difference of oil fluid properties between fractures and matrix changes up to 50%, while the difference of gas fluid properties between fractures and matrix changes around 20%.

We extended our investigations to real reservoir fluids, i.e., Bakken shale oil [5] and Marcellus shale condensate [34] while using the same simulation setup. The reservoir temperatures of Bakken shale oil and Marcellus shale condensate are at 240 and 150 °F, respectively.

The composition distribution and oil/gas viscosity and density of Bakken shale oil and Marcellus shale condensate are plotted in Figure 8, Figure 9, Figure 10 and Figure 11. The results of overall composition profiles are similar to the ones for the ternary mixture. As shown in Figure 8 and Figure 10, for both of these fluids, the composition of the light component (C₁) increases in fracture and decreases in the matrix, while the intermediate components, i.e., C₄, C₇-C₁₂ (Bakken oil), and C₄, C₇ (Marcellus condensate), transfer from the fracture to the matrix. The change of fluid properties for Bakken fluid is also similar to the ternary mixture. As shown in Figure 9, the densities and viscosities of oil in fracture and gas in matrix increase while the densities and viscosities of oil in matrix and gas in fracture decrease. However, for Marcellus shale condensate, the fluid proprieties are barely changed (Figure 11). This is because the methane composition is larger (80%) compared to other components and the change methane composition is minimal (around 3%), which had a negligible effect on the fluid properties.

In summary, due to the effect of heterogeneous pore-size distribution, molecular diffusion occurs at the fracture–matrix interface. In general, light components move from matrix region to fractures, while intermediate and heavier components migrate in the opposite direction, i.e., from fracture to matrix. We should note that the component redistribution happens for all fluids cases and the trends are similar, but the change of fluid properties varies with fluid compositions. For Bakken fluid, its density and viscosity change by 3% and 5%, respectively, but for gas condensate fluid, the density and viscosity barely change with time.

3.1.2. Inclusion of Capillary Pressure in Flow

Driven by compositional gradient only, fluid overall compositions change over time because of molecular diffusion. However, capillary pressure itself acts as a driving force and influences the composition distribution. In this section, we study the effect of capillary pressure inclusion in flow and flash on mass transfer for the ternary mixture using the same 2D simulation setup. Note that here molecular diffusion is not included. In our previous research studies [5,30] we found out that the choice of reference pressure could moderately influence the calculated fluid properties. To assure that this choice does not significantly influence the composition distributions, we examine different choices of the reference pressure ($ref=1$, $ref=0.5$ and $ref=0$) to analyze the effect on composition redistribution. Figure 12 shows the results of composition profiles with different reference pressure choices after 100 days. It is observed that the light component moves toward the bulk (fracture) region and the intermediate component moves from the fracture to matrix and this trend is the same as the previous results when diffusion is considered only. The selection of different reference pressures barely changes the composition distribution. If the reference phase was chosen to be the liquid (vapor) phase, i.e., $ref=1$ ($ref=0$), the composition difference between both sides will reach a maximum (minimum) value and the difference between the maximum and the minimum value is around 1%.

Next, the oil and gas properties are calculated with different reference pressure choices. As shown in Figure 13, for any reference pressure choice, the difference between the fluid properties at the two ends (matrix and fracture) decreases with time, and this observation is the opposite of what we observed due to diffusion only. In addition, adopting different reference pressures yields different density and viscosity distribution.

3.1.3. Diffusion and Capillary Pressure in Flow

To examine the effect of both pressure and concentration gradients, molecular diffusion and capillary pressure in flow have been incorporated in our simulation model. The ternary mixture fluid was used and the liquid pressure was selected as the reference pressure, i.e., ref = 1. The results and the comparison with previous cases are shown in Figure 14 and Figure 15. As shown in Figure 14, for the model with consideration of only diffusion or capillary pressure (Pc) in flow, the light component accumulates in the bulk (fracture) region and the concentration of the intermediate component increases in the matrix nanopores. When both driving forces are considered, the trend of composition redistribution is amplified compared to either of the single effects. The fluid properties difference at the two boundaries increase in the diffusion model but decrease in the model with capillary pressure in flow only. When both molecular diffusion and capillary pressure in flow are considered, the two effects (black and green lines) would cancel each other out and the final fluid properties (purple lines) are close to the initial case (red lines).

3.2. Slim Tube Simulations and MMP

We used slim tube simulations (1D fully compositional model) to investigate the influence of molecular diffusion and heterogeneous pore size on MMP for Bakken fluid. Three simulation cases are considered with permeabilities of i.e., 10 μd, 1 μd, and 100 nd. Other reservoir properties are given in

Table 4. Properties of slim tube simulation setup.

Cell Numbers	50 × 1
Size of the system/m	50 × 1
Initial pressure/psia	1300/1500/2000/2500/3000/3500 psi
Pore size/nm	10 µm/heterogeneous (Figure 3)
Porosity	0.06
Permeability	10 µd/1 µd/100 nd
Wells position (Injection/production)	Left end/Right end (x = 0 m/x = 50 m)

. For each case, we test different models (with and without diffusion) and different pore size distributions, i.e., homogenous (10 μm) or heterogeneous pore size (Figure 3). Note that the effect of capillary pressure is considered in both flow and flash calculations.

Figure 16, Figure 17 and Figure 18 show the recovery curves of C₅-C₆ of slim tube simulation with 10 µd, 1 µd, and 100 nd permeability, respectively. As shown in these figures, all the C₅-C₆ curves without diffusion bend approximately at the same pressure, 2600 psi, even though the pore size distributions are different. For pressures below this pressure, the C₅-C₆ recovery for the heterogeneous pore size reservoir is lower than the case with a homogenous pore size (10 nm) by 15%, but it is higher than the case with a homogenous pore size (10 µm) by 2%. For the cases with diffusion, it can be seen that the bend in the recovery curve occurs at higher pressures as permeability is decreasing. If this bending pressure is extrapolated to a permeability close to zero, as depicted in Figure 19, the extrapolated pressure is the same as the first contact minimum miscibility pressure (FCMMP) of CO₂ and Bakken oil, which is 4940 psia from the swelling test calculations shown in Figure 20. These results are consistent with the conclusion of Cronin et al. [25] who found that for diffusion-dominated systems, only FCMMP is important and MCMMP is not applicable in gas flooding of ultra-tight reservoirs. Similarly, for pressures lower than the MMP, the recovery of heterogeneous pore size reservoir is lower than 10 nm pore size homogenous reservoir but higher than 10 µm pore size homogenous case. However, for any pressure, the recovery of the case with diffusion is lower than the case without diffusion. Furthermore, for the cases with the same pore size, the recovery difference between with and without diffusion increases with decreasing of reservoir permeability. The average difference for each case is, 12% (10 µd), 20% (1 µd), and 30% (100 nd).

4. Discussion

The results showed that the heterogeneous pore size distribution in nano-porous media influences the distribution of fluid composition. The light components accumulate in the bulk region (or fracture) and the heavier components accumulate in the nanopore region (shale matrix). Meanwhile, the fluid properties also vary in these regions. Molecular diffusion and the capillary pressure driven convection are the two important mechanisms of fluid transport.

Diffusion is driven by the concentration gradient which is a result of different phase compositions in pores with different sizes. Note that diffusion tends to decrease this phase composition gradient over time until an equilibrium state is reached. In our study, heterogeneous capillary pressure enlarges the concentration gradient due to its effect on phase equilibrium. If capillary pressure is not included in phase equilibrium calculations, initially, there would not be any composition gradients for the two-phase multicomponent mixture. Initially, the fraction of light component (i.e., methane) in the gas phase in the bulk region is smaller than that in nanopores, and the composition of the intermediate component in the oil phase (i.e., butane) is larger in the bulk region compared to that in the nanopores. As shown in Figure 21a,b, diffusion reduces the composition gaps of methane in the gas phase and butane in the oil phase between the fracture and the matrix by transporting methane in the gas phase from the matrix to the fracture and butane from the fracture to the matrix. In addition, as shown in Figure 22c, such component migration within phases enlarges the difference of oil (gas) saturation between bulk and nanopore region. As a result, the overall composition redistributes by diffusion and fluid properties change accordingly.

Besides the effect of inclusion of capillary pressure in phase equilibrium, which causes composition gradients in heterogeneous porous media, the inclusion of capillary pressure in flow also helps transfer gas from the nanopores to the bulk region. If capillary pressure in flow is considered, as shown in Figure 22, for the two models with Pc in flow (black and blue lines, $ref=1$), the oil pressure in the fractures is higher than in the matrix so that oil flows from the fracture to the matrix. Meanwhile, the gas pressure is higher in nanopores (matrix) so that gas flows into the fracture until an equilibrium state is achieved. Therefore, in a heterogeneous reservoir with a pore size distribution, such as the fracture–matrix system, the intermediate components would likely migrate with the oil phase from the fracture into the matrix and light components would transport into the fracture.

Based on the results of the slim tube simulations, for the case of CO₂ displacing Bakken fluid, as reservoir permeability is decreased, the recovery of the intermediate component of Bakken fluid is reduced when molecular diffusion is considered. The CO₂ composition path as a function of dimensionless velocity is given in Figure 23. It can be seen that if diffusion is not considered, the CO₂ flood is closer to a piston-like displacement, whereas diffusion flattens the CO₂ front, which results in a less effective flood. The results also show that for an ultra-low permeability reservoir, the MMP of Bakken oil with CO₂ increases about 200 psi when diffusion is accounted for. For pressures below the MMP, the recovery of CO₂ displacement decreases as permeability becomes smaller.

In conclusion, our research suggests that in a nano-porous media with heterogeneous pore size, there will be a phase and overall compositions redistribution with diffusion and capillary pressure accounted for. The diffusion mass transfer is comparable to the convective flow only in ultra-tight rocks with nano–darcy permeability. At the matrix–fracture interface, the light components tend to move to the fracture and intermediate components tend to accumulate in the matrix. Such mass transport mechanisms are valid for different shale fluids and the fluid properties will also deviate from its original values in both fracture and matrix region. For CO₂ gas injection, as shown from the results of 1D simulations, heterogeneous pore size reservoir rarely changes the multi-contact MMP (MCMMP) but MMP increases for smaller permeabilities when diffusion is considered in the mass balance equations and it approaches the first-contact MMP (FCMMP) as permeability goes to zero, which means mass transport is completely diffusion-dominated.

5. Conclusions

The key highlights of this research are:

• For the first time, we proposed a new drive for mass transfer of two-phase oil gas multicomponent fluids in highly heterogeneous nano-porous media with pore size distribution.
• Owing to the high gas–oil capillary in nanopores, in heterogeneous porous media with a pore size distribution, phase compositions are altered, and different phase compositions are observed in pores with different sizes.
• Different phase compositions in neighboring pores (or fracture and matrix) with different pore sizes result in composition gradients and this phase composition gradient is the driving force for molecular diffusion.
• A selective component mass transfer is observed at the matrix–fracture interface.
• Such selective matrix–fracture component mass transfer is caused by diffusion while the inclusion of capillary pressure in flow will also that.
• The light components accumulate in the bulk region (or fracture) and the heavier components accumulate in the nanopore region (shale matrix). The maximum compositional change is around 10%.
• This selective component mass transfer is valid for different shale fluids and the fluid properties also deviate from original values and the maximum difference is about 5%.
• During primary recovery, diffusion is only important for ultra-tight rocks with permeabilities smaller than 1 nd. However, for gas injection, diffusion becomes important for reservoirs with hither permeabilities.
• Based on our results, the heterogeneous pore size reservoir rarely changes the multi-contact MMP.
• The value of MCMMP increases with permeability decreasing and will get to the value of FCMMP as mass transport is advection-free and completely diffusion-dominated (permeability equals to zero).