A Fractal Discrete Fracture Network Based Model for Gas Production from Fractured Shale Reservoirs
Abstract
:1. Introduction
2. Model Development
2.1. Creation of Fractal Discrete Fracture Network
2.2. Governing Equations for Multi-Physical Processes in Fractured Shale Reservoirs
2.2.1. Deformation Equation of the Fractured Shale Reservoir
2.2.2. Equation of Gas Flow in Shale Matrix
2.2.3. Gas Flow Equation in Fracture Network
2.2.4. Gas Flow Equation in Hydraulic Fractures
3. Implementation and Validation of Proposed Numerical Model
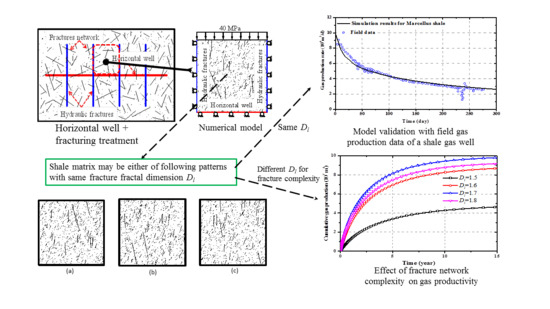
3.1. Geometry of Numerical Simulation Model
3.2. Multi-Physical Coupling During Gas Extraction
3.3. Model Reliability
3.4. Model Accuracy Check
4. Results and Discussions
4.1. Effects of Fracture Length Fractal Dimension
4.1.1. Variation of Reservoir Pressure
4.1.2. Impacts of Fracture Network on Shale Gas Production
4.2. Effects of Pore Size Distribution
4.3. Effects of Initial Fracture Permeability
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chapman, M.; Palisch, T. Fracture conductivity-Design considerations and benefits in unconventional reservoirs. J. Pet. Sci. Eng. 2014, 124, 407–415. [Google Scholar] [CrossRef]
- Patzek, T.; Male, F.; Marder, M. A simple model of gas production from hydrofractured horizontal wells in shales. AAPG Bull. 2014, 98, 2507–2529. [Google Scholar] [CrossRef]
- AlTwaijri, M.; Xia, Z.; Yu, W.; Qu, L.; Hu, Y.; Xu, Y.; Sepehrnoori, K. Numerical study of complex fracture geometry effect on two-phase performance of shale-gas wells using the fast EDFM method. J. Pet. Sci. Eng. 2018, 164, 603–622. [Google Scholar] [CrossRef]
- Wang, J.G.; Hu, B.; Liu, H.; Han, Y. Effects of ‘soft-hard’ compaction and multiscale flow on the shale gas production from a multistage hydraulic fractured horizontal well. J. Petrol. Sci. Eng. 2018, 170, 873–887. [Google Scholar] [CrossRef]
- Zhang, L.; Cui, C.; Ma, X.; Sun, Z.; Liu, F.; Zhang, K. A fractal discrete fracture network model for history matching of naturally fractured reservoirs. Fractals 2019, 27, 1–15. [Google Scholar] [CrossRef]
- Civan, F. Effective correlation of apparent gas permeability in tight porous media. Transp. Porous Media 2010, 82, 375–384. [Google Scholar] [CrossRef]
- Akkutlu, I.Y.; Fathi, E. Multiscale gas transport in shales with local kerogen heterogeneities. SPE J. 2012, 17, 1002–1011. [Google Scholar] [CrossRef] [Green Version]
- Darabi, H.; Ettehad, A.; Javadpour, F.; Sepehrnoori, K. Gas flow in ultra-tight shale strata. J. Fluid Mech. 2012, 710, 641–658. [Google Scholar] [CrossRef]
- Yu, W.; Sepehrnoori, K.; Patzek, T. Modeling gas adsorption in Marcellus shale with Langmuir and BET isotherms. SPE J. 2016, 21, 589–600. [Google Scholar] [CrossRef] [Green Version]
- Geng, L.; Li, G.; Wang, M.; Li, Y.; Tian, S.; Pang, W.; Lyu, Z. A fractal production prediction model for shale gas reservoirs. J. Nat. Gas Sci. Eng. 2018, 55, 354–367. [Google Scholar] [CrossRef]
- Hu, B.; Wang, J.G.; Li, Z.; Wang, H. Evolution of fractal dimensions and gas transport models during the gas recovery process from a fractured shale reservoir. Fractals 2019, 27, 1950129. [Google Scholar] [CrossRef]
- Hu, B.; Wang, J.G.; Wu, D.; Wang, H. Impacts of zone fractal properties on shale gas productivity of a multiple fractured horizontal well. Fractals 2019, 27, 1950006. [Google Scholar] [CrossRef]
- Wang, J.G.; Hu, B.; Wu, D.; Dou, F.; Wang, X. A multiscale fractal transport model with multilayer sorption and effective porosity effects. Transp. Porous Media 2019, 129, 25–51. [Google Scholar] [CrossRef]
- Wang, H.; Wang, J.G.; Wang, X.; Hu, B. An improved relative permeability model for gas-water displacement in fractal porous media. Water 2020, 12, 27. [Google Scholar] [CrossRef] [Green Version]
- Klimczak, C.; Schultz, R.A.; Parashar, R.; Reeves, D.M. Cubic law with aperture-length correlation: Implications for network scale fluid flow. Hydrogeol. J. 2010, 18, 851–862. [Google Scholar] [CrossRef]
- Larsen, B.; Grunnaleite, I.; Gudmundsson, A. How fracture systems affect permeability development in shallow-water carbonate rocks: An example from the Gargano Peninsula, Italy. J. Struct. Geol. 2010, 32, 1212–1230. [Google Scholar] [CrossRef]
- Ambrose, R.J.; Hartman, R.C.; Diaz-Campos, M.; Akkutlu, I.Y.; Sondergeld, C.H. Shale gas-in-place calculations part I: New pore-scale considerations. SPE J. 2012, 17, 219–229. [Google Scholar] [CrossRef]
- Jafari, A.; Babadagli, T. Estimation of equivalent fracture network permeability using fractal and statistical network properties. J. Pet. Sci. Eng. 2012, 92–93, 110–123. [Google Scholar] [CrossRef]
- Miao, T.; Yu, B.; Duan, Y.; Feng, Q. A fractal analysis of permeability for fractured rocks. Int. J. Heat Mass Transf. 2015, 81, 75–80. [Google Scholar] [CrossRef]
- Warren, J.E.; Root, P.J. The behavior of naturally fractured reservoirs. Soc. Petrol. Eng. J. 1963, 3, 245–255. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Wang, J.G.; Leung, C.F.; Gao, F. A multi-parameter optimization model for the evaluation of shale gas recovery enhancement. Energies 2018, 11, 654. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Wang, J.G.; Gao, F.; Ju, Y.; Zhang, X.; Zhang, L. Flow consistency between non-Darcy flow in fracture network and nonlinear diffusion in matrix to gas production rate in fractured shale gas reservoirs. Transp. Porous Media 2016, 111, 97–121. [Google Scholar] [CrossRef]
- Liu, J.; Wang, J.G.; Gao, F.; Leung, C.F.; Ma, Z. A fully coupled fracture equivalent continuum-dual porosity model for hydro-mechanical process in fractured shale gas reservoirs. Comput. Geotech. 2019, 106, 143–160. [Google Scholar] [CrossRef]
- Jiang, J.; Younis, R. A multimechanistic multicontinuum model for simulating shale gas reservoir with complex fractured system. Fuel 2015, 161, 333–344. [Google Scholar] [CrossRef]
- Yu, W.; Xu, Y.; Liu, M.; Wu, K.; Sepehrnoori, K. Simulation of shale gas transport and production with complex fractures using embedded discrete fracture model. AIChE J. 2018, 64, 2251–2264. [Google Scholar] [CrossRef]
- Cao, R.; Fang, S.; Jia, P.; Cheng, L.; Rao, X. An efficient embedded discrete-fracture model for 2D anisotropic reservoir simulation. J. Pet. Sci. Eng. 2019, 174, 115–130. [Google Scholar] [CrossRef]
- Akkutlu, I.Y.; Efendiev, Y.; Vasilyeva, M. Multiscale model reduction for shale gas transport in fractured media. Comput. Geosci. 2016, 20, 953–973. [Google Scholar] [CrossRef] [Green Version]
- Akkutlu, I.Y.; Efendiev, Y.; Vasilyeva, M.; Wang, Y. Multiscale model reduction for shale gas transport in a coupled discrete fracture and dual-continuum porous media. J. Nat. Gas Sci. Eng. 2017, 48, 65–76. [Google Scholar] [CrossRef]
- Odling, N.E. Scaling and connectivity of joint systems in sandstones from western Norway. J. Struct. Geol. 1997, 19, 1251–1271. [Google Scholar] [CrossRef]
- Baghbanan, A.; Jing, L. Hydraulic properties of fractured rock masses with correlated fracture length and aperture. Int. J. Rock Mech. Min. Sci. 2007, 44, 704–719. [Google Scholar] [CrossRef]
- Parashar, R.; Reeves, D. On iterative techniques for computing flow in large two-dimensional discrete fracture networks. J. Comput. Appl. Math. 2012, 236, 4712–4724. [Google Scholar] [CrossRef] [Green Version]
- Miao, T.; Chen, A.; Xu, Y.; Cheng, S.; Yu, B. A fractal permeability model for porous–fracture media with the transfer of fluids from porous matrix to fracture. Fractals 2019, 26, 1–9. [Google Scholar] [CrossRef]
- Liu, R.; Li, B.; Jiang, Y. A fractal model based on a new governing equation of fluid flow in fractures for characterizing hydraulic properties of rock fracture networks. Comput. Geotech. 2016, 75, 57–68. [Google Scholar] [CrossRef]
- Liu, R.; Yu, L.; Jiang, Y. Fractal analysis of directional permeability of gas shale fracture networks: A numerical study. J. Nat. Gas Sci. Eng. 2016, 33, 1330–1341. [Google Scholar] [CrossRef] [Green Version]
- Priest, S. Discontinuity Analysis for Rock Engineering; Springer: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Liu, H.; Rutqvist, J.; Berryman, J. On the relationship between stress and elastic strain for porous and fractured rock. Int. J. Rock Mech. Min. Sci. 2009, 46, 289–296. [Google Scholar] [CrossRef] [Green Version]
- Shang, X.; Wang, J.G.; Zhang, Z.; Gao, F. A three-parameter permeability model for cracking process of fractured rocks under temperature change and external loading. Int. J. Rock Mech. Min. Sci. 2019, 123, 104106. [Google Scholar] [CrossRef]
- Yu, W.; Sepehrnoori, K. Simulation of gas desorption and geomechanics effects for unconventional gas reservoirs. Fuel 2014, 116, 455–464. [Google Scholar] [CrossRef]














| Parameter | Value |
|---|---|
| Fracture network size (m × m) | 50 × 50 |
| Fracture length fractal dimension, Dl | 1.5–1.8 |
| Maximum fracture length, lmax (m) | 30 |
| Minimum fracture length, lmin (m) | 0.3 |
| Fisher constant, K | 5 |
| Parameters | Values |
|---|---|
| Initial reservoir gas pressure, (MPa) | 25 |
| Bottom pressure, (MPa) | 3.0 |
| Reservoir temperature, (K) | 330 |
| Thickness of fracture network model, (m) | 10 |
| Universal gas constant, (J/(mol·K)) | 8.314 |
| Molar mass of methane, (kg/mol) | 0.016 |
| Molecular diameter of methane, (nm) | 0.38 |
| Straight length of representative elementary volume (REV) in matrix, (mm) | 0.1 |
| Density of shale reservoir, (kg/m3) | 2580 |
| Young’s modulus of shale, (GPa) | 20 |
| Poisson’s ratio of shale, | 0.3 |
| Methane dynamic viscosity, (Pa·s) | 1.2 × 10−5 |
| Gas density at standard condition, (kg/m3) | 0.717 |
| Porosity of hydraulic fractures, | 0.001 |
| Permeability of hydraulic fractures, (m2) | 5 × 10−10 |
| Aperture of hydraulic fractures, (mm) | 0.3 |
| Geometry factor, | 1 |
| Initial porosity of fractures, | 0.005 |
| Initial permeability of fractures, (m2) | 5 × 10−13 |
| Proportionality coefficient, | 0.001 |
| Compressibility of the fractures, (1/MPa) | 5.0 × 10−4 |
| Fracture aperture of the “hard” part, (mm) | 0.1 |
| Fracture aperture of the “soft” part, (mm) | 0.1 |
| Initial fracture aperture, (mm) | 0.1 |
| Adsorption volume in monolayer, (cm3/g) | 1.63 |
| Pseudo-saturation pressure, (MPa) | 100 |
| Number of adsorption layer, | 5.54 |
| Constant, | 26.39 |
| Porosity of adsorbed gas, | 0.05 |
| Porosity of shale matrix, | 0.15 |
| Diameter fractal dimension, | 2.7 |
| Tortuosity fractal dimension, | 1.1 |
| Maximum pore diameter, (nm) | 1000 |
| Minimum pore diameter, (nm) | 10 |
| Sorption-induced strain coefficient, (kg/m3) | 0.75 |
| Surface diffusion coefficient, (m2/s) | 1 × 10−10 |
| Biot’s coefficient of matrix, | 0.5 |
| Biot’s coefficient of fractures, | 0.5 |
| Parameters | Marcellus Shale | Barnett Shale | Unit |
|---|---|---|---|
| Initial reservoir gas pressure | 34.5 | 20.34 | MPa |
| Bottom pressure | 2.4 | 3.69 | MPa |
| Porosity of hydraulic fractures | 1 × 10−6 | 1 × 10−6 | |
| Permeability of hydraulic fractures | 3 × 10−10 | 5 × 10−9 | m2 |
| Initial porosity of fractures | 0.005 | 0.002 | |
| Initial permeability of fractures | 1 × 10−20 | 1.9×10−13 | |
| Adsorption volume in monolayer | 1.63 | 1.18 | cm3/g |
| Porosity of shale matrix | 0.15 | 0.15 | |
| Fracture length fractal dimension | 1.5 | 1.7 | |
| Diameter fractal dimension | 2.85 | 2.64 | |
| Tortuosity fractal dimension | 1.1 | 1.2 | |
| Maximum pore diameter | 600 | 1000 | nm |
| Minimum pore diameter | 10 | 10 | nm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, B.; Wang, J.; Ma, Z. A Fractal Discrete Fracture Network Based Model for Gas Production from Fractured Shale Reservoirs. Energies 2020, 13, 1857. https://doi.org/10.3390/en13071857
Hu B, Wang J, Ma Z. A Fractal Discrete Fracture Network Based Model for Gas Production from Fractured Shale Reservoirs. Energies. 2020; 13(7):1857. https://doi.org/10.3390/en13071857
Chicago/Turabian StyleHu, Bowen, Jianguo Wang, and Zhanguo Ma. 2020. "A Fractal Discrete Fracture Network Based Model for Gas Production from Fractured Shale Reservoirs" Energies 13, no. 7: 1857. https://doi.org/10.3390/en13071857
APA StyleHu, B., Wang, J., & Ma, Z. (2020). A Fractal Discrete Fracture Network Based Model for Gas Production from Fractured Shale Reservoirs. Energies, 13(7), 1857. https://doi.org/10.3390/en13071857