1. Introduction
Power electronic converters in tidal turbine drive trains regulate the power capture from the turbine, and convert the generated electricity into a grid compliant form at fixed voltage and frequency. The converter can be placed either onshore, on floating platforms, or they can be seabed-mounted adjacent to the generator. In this paper we consider the seabed-mounted converter as shown in
Figure 1. This configuration is more suitable for array applications as it minimizes cabling costs [
1], involves no hanging cables, and is out of view. However, submerged power converter also means limited access for maintenance, and hence reliability is paramount [
1]. Improving reliability, and thus capacity factor, could be a major contributor to lowering the levelized cost of energy (LCoE) from tidal turbines [
2]. According to Reference [
1], subsea converters for tidal farms will demand more than 5-year mean period between failures.
Due to similar operating principle, it is reasonable to assume that many modes of failures in tidal turbines would be similar to wind turbines (WTs). However, the frequency of occurrences of these expected failure modes may differ in each case. Multiple studies have identified converters as one of the most frequently failing subsystem in WTs [
3,
4]. Among converter components, phase modules (insulated gate bipolar transistors (IGBTs), gate-drive circuits, capacitors) were found to be more critical in terms of failure frequency [
3,
5,
6].
Thermal cycling has been identified as one of the main reasons for failure in IGBT power modules [
3,
7,
8,
9,
10]. Early failures from thermal cycling stresses can be prevented by cooling power modules [
3,
9,
10]. This cooling can be provided either by active methods such as forced-water cooling, or by passive cooling. By passive cooling we mean a system where no active devices such as pumps or fans and so forth. are used to cool the power modules. A simple possible example is to use a sealed enclosure inside which the power electronics module is bolted/welded to its walls, as shown in
Figure 2 [
11,
12]. In this case the heat is conducted from the power module base plate to the walls of the enclosure and finally dumped in the ambient seawater by natural convection.
The main objective of this paper is to analyze whether passive cooling is a feasible option for a subsea converter from the reliability viewpoint. The reliability analysis is based on estimating the lifetime of the IGBT power modules in a tidal turbine converter, considering thermal cycling as the main failure mode. In this regard, the effect of turbulence in the tidal stream velocity and surface waves on the converter lifetime is analyzed.
Liu et al. [
13] consider the reliability of the power converter in a doubly-fed induction generator based tidal turbine. They show the impact of probability distribution of tidal velocity on the converter reliability. Ren et al. [
14] use a sequential Monte-Carlo simulation-based method to quantify effects of wake on tidal generator systems reliability in a tidal current farm. However, these studies do not specifically target the lifetime damage from thermal cycling in power converters, nor do they incorporate effects of turbulence or surface waves on the converter lifetime.
Extensive research has been carried out to study the lifetime models of power modules based on thermal cycling [
15,
16,
17,
18]. Nowadays, a priori estimation of lifetime is considered a logical step in designing reliable power electronic systems [
9,
19,
20].
Shipurkar et al. [
6] compared different 3-level converter topologies for WT converters based on thermal lifetime models. Reliability of WT converters ranging from the influence of mission profiles to that of reactive power on the lifetime of IGBT modules, and comparison of multilevel converter topologies, and so forth [
19,
21,
22,
23] is also widely studied. Active control of cooling systems, switching frequency and modulation strategies, and power loss redistribution (in case of parallel converters) are some commonly used techniques to improve lifetime in WT converters [
24,
25,
26]. Adding redundancy is another way of improving the overall reliability in WT converters and subsea applications [
1,
27].
Most of the aforementioned WT lifetime studies cover mutli-MW pitch controlled turbines with 3-level medium voltage drives cooled by active methods (either water or air-cooled). This is the most common topology in modern WTs. However, active cooling mechanism usually suffer from drawbacks such as pump failure and leakage of the coolant, and so forth, which compromises the reliability to a certain degree.
The power converter under study in this paper is different from a WT converter for the following reasons. Firstly, this study considers a passively cooled submerged converter to minimize potential fault points. For tidal turbines with submerged converter, an active cooling method is unsuitable due to high maintenance costs, and limited opportunities for maintenance. Secondly, modern WTs usually employ pitch control, which makes the converter design different from a tidal turbine converter with active speed stall control investigated here. Thirdly, effects of site parameters, such as turbulence and waves on sea surface, is likely to have more impact on tidal turbine converters than on WT converters because of the higher speed oscillations in smaller scale tidal turbines. Finally, an exhaustive lifetime analysis on the tidal turbines is missing in the literature.
Thermal cycling is not the only failure mechanism in IGBT modules. Fischer et al. [
5] identified ambient humidity and moisture as the dominant failure mechanism in WT converters. However, in their study majority of the converters were liquid-cooled. On the other hand, hermetically sealed converters are less likely to fail due to moisture, which is the case with subsea power converters analysed in this study. Other failure mechanisms include corrosion, dielectric breakdown, and so forth [
27]. These failure mechanisms, however are extraneous to this study. For deep subsea applications (>100 m) power converters are enclosed in pressurized enclosures [
28,
29]. However, tidal turbines are rarely deployed at this depth, hence, we do not consider pressurized power converters in this study.
The IGBT power packs considered in this study are packed in the form of power modules rather than discs. Despite low potential for cooling, modules are preferred because of better assembly, integrated packaging, and good electrical isolation between the chip and the heat sink, and most importantly low cost compared to other packaging methods [
30].
The main contributions from this paper, therefore, are:
- –
To assess the effect of turbulence and surface waves on the lifetime of semiconductor components for a passively cooled power converter coupled to a tidal turbine;
- –
To demonstrate the effect of active speed stall control and lower inertia of tidal turbines on the generator side converter lifetime; and to propose a methodology for faster lifetime calculation in a passively cooled converter.
To the best of our knowledge, these factors are for the first time being addressed in the literature.
The following section defines the parameters adopted for characterizing the site conditions of a typical tidal site. In
Section 3, the description of the tidal turbine energy conversion system used for analysis is given.
Section 4 describes the methodology adopted for the calculation of lifetime in passively cooled power converter.
Section 5 briefly explains the thermal model of a seawater based passive cooling system.
Section 6 gives the results of a case study carried on a 110 kW tidal turbine system. Conclusions from the paper are given in
Section 7.
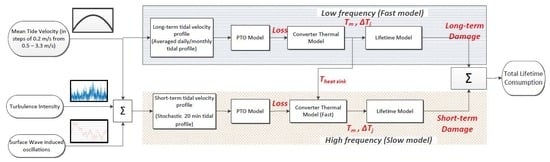
4. Lifetime Modeling of Power Modules: Methodology
Lifetime analyses for wind energy converters based on active water cooling systems has been widely studied [
6,
18,
19]. Because the passive cooling system is considered here, this means that the lifetime calculation has to be done in a slightly modified manner. This is due to the longer time constant of the passive cooling system. The main methodology is shown in
Figure 11. The calculations are performed in time domain. The temperature cycles are then calculated using the rainflow counting algorithm [
18,
45].
The high thermal capacitance of the enclosure wall makes the thermal models relatively slow in terms of computation time. For the short-term cycling, these computations are accelerated in this paper by assuming that the enclosure wall is at a constant temperature as long as the mean tidal velocity remains constant. The idea is to obtain the wall temperature from the model taking only mean tidal velocity variation into account. This wall temperature information is then used as a boundary condition in the fast converter thermal model to estimate the junction temperature cycling near the power frequency. This is illustrated in
Figure 11.
Thermal cycling can be divided into two main categories: long-term and short-term. By long term cycling we mean cycles due to variation in tidal current speeds over 12-hourly cycles, and variations due to the spring and neap tide cycles, as shown in
Figure 4. Although monthly and/or yearly variations in the tides can also be included, these have been neglected in this analysis, as their impact is expected to be negligible. Short-term cycling mainly refers to power-frequency thermal cycling and other oscillations due to turbulence and surface waves in the mean tidal stream velocity.
The lifetime estimation in this work has been based on the models presented in References [
6,
15]. These models give the number of thermal cycles to failure as a function of various parameters, with emphasis on junction temperature cycling and its mean value as per the following equation:
is the number of cycles to failure,
is the mean junction temperature, and
is the on-pulse duration,
I current per wire,
V is the chip blocking voltage and
D is the bonding wire diameter. The constants,
A,
to
are obtained from Reference [
30], and take the following values:
A = 9.34 × 10
for IGBT4 modules, [
] = [−4.416, 1.285 × 10
, −0.463, −0.716, −0.761, −0.5].
The lifetime calculation is based on junction temperature of the IGBT and the diode. These values are calculated from the thermal model of the converter explained in the next section. After the calculation of thermal cycles, the number of cycles to failure are calculated based on the Miner’s rule [
19]. That is,
where,
is the number of cycles to failure at the temperature cycle
, and
is the number of cycles to failures for the same amplitude and same stress type. The number of cycles for each thermal cycling amplitude are obtained from Equation (
6).
Figure 13 shows how
typically varies with
for constant
.
Following assumptions have been made in this analysis to reduce the calculation time:
A constant seawater temperature of 15 C was assumed, neglecting variation in annual temperature.
A constant turbulence value has been used for each mean tidal velocity, as already mentioned in
Section 2.
The turbine under consideration is an active speed stall controlled one, with no yawing capabilities. It is assumed that the performance of the turbine drops negligibly between the flood and ebb tides. Hence, as far as turbine characteristics are concerned, no distinction is made between the flood and ebb tides.
At the beginning of each flood and ebb tide cycle, the junction temperature of the IGBT module is same as the ambient temperature.
A constant power factor of operation (0.9) is assumed on the grid-side converter. In other words, effects of varying reactive power on thermal cycling have been neglected [
27].
5. Estimation of Junction Temperatures
The mean junction temperature and its amplitude about the mean value are obtained from the thermal models of the passively cooled converter [
11]. The losses inside the IGBT and diode comprise of the conduction and the switching losses given by the following equations [
27]:
where,
and
denote the conduction and switching losses respectively in the device ’k’.
and
represent the forward voltage drops in the IGBT and diode respectively, whereas
i is the component current.
is the duty ratio of the switch ’k’. And,
and
is the on and off switching energy of the device ’k’; and
is the switching frequency. Parameters for the loss calculations can be found in datasheets for IGBT modules in Reference [
46]. Details on loss calculation in the IGBT and diodes can be found in multiple references, such as References [
6,
19,
27].
The RC-thermal network of the submerged power converter with IGBT mounted on a Cu mounting plate (see
Figure 2) inside the sealed enclosure is shown in
Figure 14 [
11]. Calculation of the thermal resistances shown in
Figure 14 have been explained in Reference [
11]. For the sake of brevity, the mathematical details of the thermal model are omitted from this paper. However, a qualitative description is given below.
Heat transfer from the IGBT junction to the ambient seawater encounters three main thermal resistances (networks): IGBT junction-to-case, case-to-external wall, external wall-to-ambient water. The junction-to-case thermal network is represented typically by a 4-layer Foster network given in the datasheet of the IGBT module [
46]. However, Foster models cannot be directly connected to the RC-ladder network of the rest of the thermal network. Therefore, a slightly modified approach using a 1-layer equivalent network, as explained in References [
11,
47] is adopted as shown in
Figure 14.
The mounting plate and the enclosure wall thermal impedances include the case-to-external wall impedances. These can be represented by one-dimensional thermal resistance together with the spreading resistances in the mounting plate and the enclosure wall [
11,
48]. These spreading resistances form the bulk of the thermal resistance in case of the passively cooled submerged power converters. Proper selection of the mounting plate material and dimensions can significantly reduce the spreading resistance, as discussed in Reference [
11]. The thermal capacitance calculations of the mounting plate and the wall are simply calculated using the heat capacity of these blocks.
And finally, the wall-to-ambient seawater thermal resistance is calculated using empirical relations [
49], and a few steady state computational fluid dynamics (CFD) simulations, as explained in Reference [
11]. The convective heat transfer coefficient is a function of the mean power loss and/or wall temperature. The enclosure wall resistance is thus a dynamic variable, and needs to be recalculated continuously.
Whereas for the forced water cooling methods the case to ambient thermal resistance is almost independent of the heat loss in the power module, same cannot be said for the passively cooled converter. For the latter, heat transfer coefficient at the external wall of enclosure is a function of the heat flux from the power module [
11]. Commonly encountered values of case to ambient thermal resistance for forced water cooled systems falls in the range of 0.005–0.020 K/W. In this study, depending on the heat loss this thermal resistance falls in the range of 0.02–0.1 K/W. The case to seawater thermal resistance decreases with increase in loss in the power module. Please note that increased thermal resistance in passive cooling is accompanied by improved reliability due to no moving parts.