Real-Time Reconstruction of Contaminant Dispersion from Sparse Sensor Observations with Gappy POD Method
Abstract
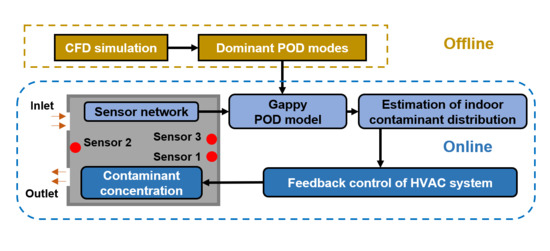
:1. Introduction
2. Materials and Methods
2.1. Standard POD
2.2. Gappy POD
2.3. Sensor Placement
2.4. Numerical Model
2.5. Model Setup
3. Results
3.1. POD Decomposition
3.2. Sensor Placement
3.3. Gappy Flow Reconstruction
4. Discussions and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lim, E.; Ito, K.; Sandberg, M. Performance evaluation of contaminant removal and air quality control for local ventilation systems using the ventilation index Net Escape Velocity. Build. Environ. 2014, 79, 78–89. [Google Scholar] [CrossRef]
- Kolokotsa, D.; Pouliezos, A.; Stavrakakis, G.; Lazos, C. Predictive control techniques for energy and indoor environmental quality management in buildings. Build. Environ. 2009, 44, 1850–1863. [Google Scholar] [CrossRef]
- Lee, S.; Hwangbo, S.; Kim, J.T.; Yoo, C.K. Gain scheduling based ventilation control with varying periodic indoor air quality (IAQ) dynamics for healthy IAQ and energy savings. Energy Build. 2017, 153, 275–286. [Google Scholar] [CrossRef]
- Tong, Z.; Chen, Y.; Malkawi, A.; Liu, Z.; Freeman, R.B. Energy saving potential of natural ventilation in China: The impact of ambient air pollution. Appl. Energy 2016, 179, 660–668. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Du, J.; Soleymanzadeh, E. Model predictive control of commercial buildings in demand response programs in the presence of thermal storage. J. Clean. Prod. 2019, 218, 315–327. [Google Scholar] [CrossRef]
- King, J.; Perry, C. Smart Buildings: Using Smart Technology to Save Energy in Existing Buildings; Amercian Council for an Energy-Efficient Economy: Washington, DC, USA, 2017. [Google Scholar]
- Hu, S.; Hoare, C.; Raftery, P.; O’Donnell, J. Environmental and energy performance assessment of buildings using scenario modelling and fuzzy analytic network process. Appl. Energy 2019, 255, 113788. [Google Scholar] [CrossRef]
- Li, K.; Su, H. Forecasting building energy consumption with hybrid genetic algorithm-hierarchical adaptive network-based fuzzy inference system. Energy Build. 2010, 42, 2070–2076. [Google Scholar] [CrossRef]
- Manohar, K.; Brunton, B.W.; Kutz, J.N.; Brunton, S.L. Data-Driven Sparse Sensor Placement for Reconstruction: Demonstrating the Benefits of Exploiting Known Patterns. IEEE Contr. Syst. Mag. 2018, 38, 63–86. [Google Scholar]
- Burrough, P.A.; McDonnell, R.; McDonnell, R.A.; Lloyd, C.D. Principles of Geographical Information Systems; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Huang, Y.; Shen, X.; Li, J.; Li, B.; Duan, R.; Lin, C.H.; Chen, Q. A method to optimize sampling locations for measuring indoor air distributions. Atmos. Environ. 2015, 102, 355–365. [Google Scholar] [CrossRef]
- Li, J.; Li, H.; Ma, Y.; Wang, Y.; Abokifa, A.A.; Lu, C.; Biswas, P. Spatiotemporal distribution of indoor particulate matter concentration with a low-cost sensor network. Build. Environ. 2018, 127, 138–147. [Google Scholar] [CrossRef]
- Cheng, K.-C.; Tseng, C.-H.; Hildemann, L.M. Using Indoor Positioning and Mobile Sensing for Spatial Exposure and Environmental Characterizations: Pilot Demonstration of PM2. 5 Mapping. Environ. Sci. Technol. Lett. 2019, 6, 153–158. [Google Scholar] [CrossRef]
- Kosutova, K.; van Hooff, T.; Vanderwel, C.; Blocken, B.; Hensen, J. Cross-ventilation in a generic isolated building equipped with louvers: Wind-tunnel experiments and CFD simulations. Build. Environ. 2019, 154, 263–280. [Google Scholar] [CrossRef]
- Aganovic, A.; Steffensen, M.; Cao, G. CFD study of the air distribution and occupant draught sensation in a patient ward equipped with protected zone ventilation. Build. Environ. 2019, 162, 106279. [Google Scholar] [CrossRef]
- Liu, W.; Liu, D.; Gao, N. CFD study on gaseous pollutant transmission characteristics under different ventilation strategies in a typical chemical laboratory. Build. Environ. 2017, 126, 238–251. [Google Scholar] [CrossRef]
- Zuo, W.; Chen, Q. Real-time or faster-than-real-time simulation of airflow in buildings. Indoor Air 2009, 19, 33. [Google Scholar] [CrossRef] [Green Version]
- Zuo, W.; Chen, Q. Fast and informative flow simulations in a building by using fast fluid dynamics model on graphics processing unit. Build. Environ. 2010, 45, 747–757. [Google Scholar] [CrossRef]
- Zuo, W.; Chen, Q. Simulations of Air Distributions in Buildings by FFD on GPU. HVAC&R Res. 2010, 16, 785–798. [Google Scholar]
- Xue, Y.; Liu, W.; Wang, Q.; Bu, F. Development of an integrated approach for the inverse design of built environment by a fast fluid dynamics-based generic algorithm. Build. Environ. 2019, 160, 106205. [Google Scholar] [CrossRef]
- Liu, W.; Jin, M.; Chen, C.; You, R.; Chen, Q. Implementation of a fast fluid dynamics model in OpenFOAM for simulating indoor airflow. Numer. Heat Transf. Part A Appl. 2016, 69, 748–762. [Google Scholar] [CrossRef]
- Jin, M.; Zuo, W.; Chen, Q. Improvements of Fast Fluid Dynamics for Simulating Air Flow in Buildings. Numer. Heat Transf. Part B Fundam. 2012, 62, 419–438. [Google Scholar] [CrossRef]
- Megri, C.A.; Haghighat, F. Zonal modeling for simulating indoor environment of buildings: Review, recent developments, and applications. HVAC&R Res. 2007, 13, 887–905. [Google Scholar]
- Jiru, E.T.; Haghighat, F. Modeling ventilated double skin façade—A zonal approach. Energy Build. 2008, 40, 1567–1576. [Google Scholar] [CrossRef]
- Song, Z.; Murray, B.T.; Sammakia, B. A dynamic compact thermal model for data center analysis and control using the zonal method and artificial neural networks. Appl. Therm. Eng. 2014, 62, 48–57. [Google Scholar] [CrossRef]
- Chen, Q. Ventilation performance prediction for buildings: A method overview and recent applications. Build. Environ. 2009, 44, 848–858. [Google Scholar] [CrossRef]
- Song, Z.; Murray, B.T.; Sammakia, B. Airflow and temperature distribution optimization in data centers using artificial neural networks. Int. J. Heat Mass Transf. 2013, 64, 80–90. [Google Scholar] [CrossRef]
- Cao, S.-J.; Ren, C. Ventilation control strategy using low-dimensional linear ventilation models and artificial neural network. Build. Environ. 2018, 144, 316–333. [Google Scholar] [CrossRef]
- Zhou, L.; Haghighat, F. Optimization of ventilation system design and operation in office environment, Part I: Methodology. Build. Environ. 2009, 44, 651–656. [Google Scholar] [CrossRef]
- Zhou, L.; Haghighat, F. Optimization of ventilation systems in office environment, Part II: Results and discussions. Build. Environ. 2009, 44, 657–665. [Google Scholar] [CrossRef]
- Oberleithner, K.; Sieber, M.; Nayeri, C.N.; Paschereit, C.O.; Petz, C.; Hege, H.C.; Wygnanski, I. Three-dimensional coherent structures in a swirling jet undergoing vortex breakdown: Stability analysis and empirical mode construction. J. Fluid Mech. 2011, 679, 383–414. [Google Scholar] [CrossRef] [Green Version]
- Lengani, D.; Simoni, D.; Pichler, R.; Sandberg, R.D.; Michelassi, V.; Bertini, F. Identification and quantification of losses in a LPT cascade by POD applied to LES data. Int. J. Heat Fluid Flow 2018, 70, 28–40. [Google Scholar] [CrossRef]
- Kumar, N.; Burton, T.D. Use of random excitation to develop POD based reduced order models for nonlinear structural dynamics. In Proceedings of the ASME 2007 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Las Vegas, NV, USA, 4–7 September 2007; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2007. [Google Scholar]
- Cao, Y.; Zhu, J.; Luo, Z.; Navon, I.M. Reduced-Order Modeling of the Upper Tropical Pacific Ocean Model using Proper Orthogonal Decomposition. Comput. Math. Appl. 2006, 52, 1373–1386. [Google Scholar] [CrossRef] [Green Version]
- Luo, Z.; Zhu, J.; Wang, R.; Navon, I.M. Proper orthogonal decomposition approach and error estimation of mixed finite element methods for the tropical Pacific Ocean reduced gravity model. Comput. Methods Appl. Mech. Eng. 2007, 196, 4184–4195. [Google Scholar] [CrossRef]
- Brunton, S.L.; Kutz, J.N. Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control; Cambridge University Press: Chambridge, UK, 2019. [Google Scholar]
- Willcox, K. Unsteady flow sensing and estimation via the gappy proper orthogonal decomposition. Comput. Fluids 2006, 35, 208–226. [Google Scholar] [CrossRef] [Green Version]
- Tallet, A.; Allery, C.; Allard, F. POD approach to determine in real-time the temperature distribution in a cavity. Build. Environ. 2015, 93, 34–49. [Google Scholar] [CrossRef]
- Jiang, C.; Soh, Y.C.; Li, H. Two-stage indoor physical field reconstruction from sparse sensor observations. Energy Build. 2017, 151, 548–563. [Google Scholar] [CrossRef]
- Meyer, R.D.; Tan, G. Provide detailed and real-time indoor environmental information using POD–LSE and limited measurements. Energy Build. 2014, 73, 59–68. [Google Scholar] [CrossRef]
- Li, K.; Su, H.; Chu, J.; Xu, C. A fast-POD model for simulation and control of indoor thermal environment of buildings. Build. Environ. 2013, 60, 150–157. [Google Scholar] [CrossRef]
- Sempey, A.; Inard, C.; Ghiaus, C.; Allery, C. Fast simulation of temperature distribution in air conditioned rooms by using proper orthogonal decomposition. Build. Environ. 2009, 44, 280–289. [Google Scholar] [CrossRef]
- Phan, L.; Lin, C.-X. Reduced order modeling of a data center model with multi-Parameters. Energy Build. 2017, 136, 86–99. [Google Scholar] [CrossRef]
- Allery, C.; Béghein, C.; Hamdouni, A. Applying proper orthogonal decomposition to the computation of particle dispersion in a two-dimensional ventilated cavity. Commun. Nonlinear Sci. Numer. Simul. 2005, 10, 907–920. [Google Scholar] [CrossRef]
- Bui-Thanh, T.; Damodaran, M.; Willcox, K. Proper Orthogonal Decomposition Extensions for Parametric Applications in Compressible Aerodynamics. In Proceedings of the 21st AIAA Applied Aerodynamics Conference, Orlando, FL, USA, 23–26 June 2003; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2003. [Google Scholar]
- Sirovich, L. Turbulence and the dynamics of coherent structures. I. Coherent structures. Q. Appl. Math. 1987, 45, 561–571. [Google Scholar]
- Ye, X.; Kang, Y.; Yang, F.; Zhong, K. Comparison study of contaminant distribution and indoor air quality in large-height spaces between impinging jet and mixing ventilation systems in heating mode. Build. Environ. 2019, 160, 106159. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, Q.; Glicksman, L.R.; Hu, Y.; Yang, X. Measurements and computations of room airflow with displacement ventilation. Ashrae Trans. 1999, 105, 340. [Google Scholar]
- Stull, R.B. Review of non-local mixing in turbulent atmospheres: Transilient turbulence theory. Bound.-Lay. Meteorol. 1993, 62, 21–96. [Google Scholar] [CrossRef]
- Sun, X.-H.; Xu, M.-H. Optimal control of water flooding reservoir using proper orthogonal decomposition. J. Comput. Appl. Math. 2017, 320, 120–137. [Google Scholar] [CrossRef]
- Tong, Z.; Chen, Y.; Malkawi, A.; Adamkiewicz, G.; Spengler, J.D. Quantifying the impact of traffic-related air pollution on the indoor air quality of a naturally ventilated building. Environ. Int. 2016, 89, 138–146. [Google Scholar] [CrossRef]
- Tong, S.; Huang, Y.; Tong, Z.; Cong, F. A novel short-frequency slip fault energy distribution-based demodulation technique for gear diagnosis and prognosis. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420915032. [Google Scholar] [CrossRef]
- Tong, S.; Cheng, Z.; Cong, F.; Tong, Z.; Zhang, Y. Developing a grid-connected power optimization strategy for the integration of wind power with low-temperature adiabatic compressed air energy storage. Renew. Energy 2018, 125, 73–86. [Google Scholar] [CrossRef]
- Cheng, Z.; Tong, S.; Tong, Z. Bi-directional nozzle control of multistage radial-inflow turbine for optimal part-load operation of compressed air energy storage. Energy Convers. Manag. 2019, 181, 485–500. [Google Scholar] [CrossRef]
- Tong, Z.M.; Xin, J.G.; Tong, S.G.; Yang, Z.Q.; Zhao, J.Y.; Mao, J.H. Internal flow structure, fault detection, and performance optimization of centrifugal pumps. J. Zhejiang Univ. Sci. A 2020, 21, 85–117. [Google Scholar] [CrossRef]







© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, Z.; Li, Y. Real-Time Reconstruction of Contaminant Dispersion from Sparse Sensor Observations with Gappy POD Method. Energies 2020, 13, 1956. https://doi.org/10.3390/en13081956
Tong Z, Li Y. Real-Time Reconstruction of Contaminant Dispersion from Sparse Sensor Observations with Gappy POD Method. Energies. 2020; 13(8):1956. https://doi.org/10.3390/en13081956
Chicago/Turabian StyleTong, Zheming, and Yue Li. 2020. "Real-Time Reconstruction of Contaminant Dispersion from Sparse Sensor Observations with Gappy POD Method" Energies 13, no. 8: 1956. https://doi.org/10.3390/en13081956
APA StyleTong, Z., & Li, Y. (2020). Real-Time Reconstruction of Contaminant Dispersion from Sparse Sensor Observations with Gappy POD Method. Energies, 13(8), 1956. https://doi.org/10.3390/en13081956