A Comparative Study of Solar-Driven Trigeneration Systems for the Building Sector
Abstract
:1. Introduction
2. Materials and Methods
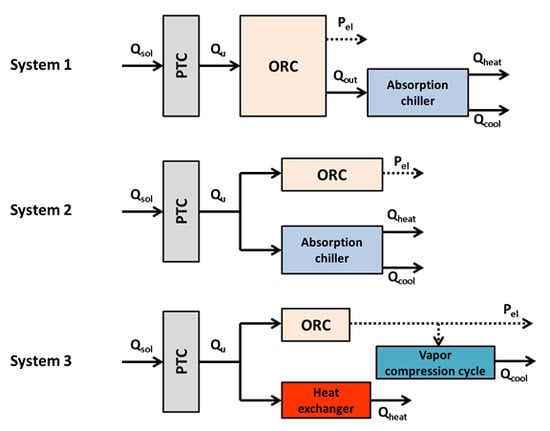
2.1. The Examined Systems
2.2. Basic Mathematical Modeling
2.3. Followed Methodology
3. Results and Discussion
3.1. Sensitivity Analysis of the Three Systems
3.2. Optimization of the Three Systems
4. Conclusions
- -
- System 1 presents 78.17% energy efficiency, System 2 43.30% and System 3 37.45%. Thus, System 1 is the best choice energetically.
- -
- System 1 presents 15.94% exergy efficiency, System 2 13.08% and System 3 8.49%. These results indicate that System 1 is the best choice exergetically.
- -
- The simple payback period is found to be 5.62 years for System 1, 7.82 years for System 2 and 8.49 years for System 9. So, System 1 is the best choice financially.
- -
- The electricity production in System 1 is 6.05 kW, the heating production is 25.28 kW and the cooling production is 23.39. The heating and the cooling production of this system are higher than the other systems with a significant difference. The electricity production is similar to the other systems but it is a bit lower.
- -
- System 1 is found to be the optimum system according to all the criteria (SPP, energy efficiency and exergy efficiency), while System 2 is the second choice and System 3 is the last choice. However, all the systems are found to be financially viable.
Author Contributions
Funding
Acknowledgments

Conflicts of Interest
Nomenclature
| Acol | Collecting area, m2 |
| C0 | Capital cost, € |
| CF | Yearly cash flow income, € |
| Gb | Solar direct beam irradiation, W/m2 |
| h | Specific enthalpy, kJ/kg |
| K | Incident angle modifier, - |
| Kach | Specific cost of the absorption chiller, €/kWcool |
| Kcol | Specific cost of the collector, €/m2 |
| Kel | Electricity cost, €/kWhel |
| Kcool | Cooling cost, €/kWhcool |
| Kheat | Heating cost, €/kWhheat |
| Khex | Cost of the heat exchanger for heating production, € |
| Korc | Specific cost of the organic Rankine cycle, €/kWel |
| KO&M | Yearly cost for operation and maintenance, € |
| Ktank | Specific cost of the storage tank, €/m3 |
| m | Mass flow rate, kg/s |
| mr | Refrigerant Mass flow rate, kg/s |
| pcrit | Critical pressure of the working fluid, bar |
| ph | Pressure in the turbine inlet, bar |
| Pel | Electricity production, kWel |
| Q | Heat rate, kW |
| SPP | Simple Payback Period, years |
| T | Temperature, °C |
| Time | Yearly operating period of the system, h |
| V | Storage tank volume, m3 |
| Wp | Electricity consumption of the pump motor, kW |
| WT | Turbine work production, kW |
| X | LiBr mass concentration, % |
| Greek Symbols | |
| α | Ratio of the turbine inlet pressure to the critical pressure, - |
| ΔP | Pressure increase in the heat pump, bar |
| η | Efficiency, - |
| ηg | Electrical generator efficiency, - |
| ηhex | Solution heat exchanger efficiency, - |
| ηm | Mechanical efficiency, - |
| ηmotor | Motor efficiency, - |
| θ | Incident solar angle, ° |
| ρ | Density, kg/m3 |
| Subscripts and Superscripts | |
| am | Ambient |
| c | Condenser of the absorption chiller |
| col | Collector |
| com | Compressor |
| cond | Condenser of the vapor compression cycle |
| cool | Cooling production |
| devices | Devices of the total system |
| el | Electricity production |
| en | Energy |
| ex | Exergy |
| f | Fluid |
| heat | Heating production |
| is | Isentropic |
| loss | Tank losses |
| orc | Organic Rankine cycle |
| sol | Solar |
| st | Storage |
| str | Strong |
| sun | Sun |
| T | Turbine |
| th | Thermal |
| u | Useful |
| w | Weak |
| Abbreviations | |
| ACH | Absorption Chiller |
| EES | Engineering Equation Solver |
| HRS | Heat Recovery System |
| ORC | Organic Rankine Cycle |
| PTC | Parabolic Trough Collector |
| VCC | Vapor Compression Cycle |
Appendix A. Basic Modeling of the Organic Rankine Cycle

Appendix B. Basic Modeling of the Absorption Chiller

Appendix C. Basic Modeling of the Vapor Compression Cycle

References
- Wang, F.; Cheng, Z.; Tan, J.; Yuan, Y.; Shuai, Y.; Liu, L. Progress in concentrated solar power technology with parabolic trough collector system: A comprehensive review. Renew. Sustain. Energy Rev. 2017, 79, 1314–1328. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C. Alternative designs of parabolic trough solar collectors. Prog. Energy Combust. Sci. 2019, 71, 81–117. [Google Scholar] [CrossRef]
- Zhang, M.; Ge, X.; Zhao, Y.; Xia-Bauer, C. Creating statistics for China’s building energy consumption using an adapted energy balance shee. Energies 2019, 12, 4293. [Google Scholar] [CrossRef] [Green Version]
- Kasaeian, A.; Nouri, G.; Ranjbaran, P.; Wen, D. Solar collectors and photovoltaics as combined heat and power systems: A critical review. Energy Convers. Manag. 2018, 156, 688–705. [Google Scholar] [CrossRef] [Green Version]
- Wu, D.W.; Wang, R.Z. Combined cooling, heating and power: A review. Prog. Energy Combust. Sci. 2006, 32, 459–495. [Google Scholar] [CrossRef]
- Al-Sulaiman, F.A.; Dincer, I.; Hamdullahpur, F. Exergy modeling of a new solar driven trigeneration system. Sol. Energy 2011, 85, 2228–2243. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C. Parametric analysis and optimization of a solar driven trigeneration system based on ORC and absorption heat pump. J. Clean. Prod. 2017, 161, 493–509. [Google Scholar] [CrossRef]
- Eisavi, B.; Khalilarya, S.; Chitsaz, A.; Rosen, M.A. Thermodynamic analysis of a novel combined cooling, heating and power system driven by solar energy. Appl. Therm. Eng. 2018, 129, 1219–1229. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, Y.; Deng, S.; Ni, J.; Xu, W.; Ma, M.; Lin, S.; Yu, Z. Solar driven ORC-based CCHP: Comparative performance analysis between sequential and parallel system configurations. Appl. Therm. Eng. 2018, 131, 697–706. [Google Scholar] [CrossRef]
- Khalid, F.; Dincer, I.; Rosen, M.A. Techno-economic assessment of a renewable energy based integrated multigeneration system for green buildings. Appl. Therm. Eng. 2016, 99, 1286–1294. [Google Scholar] [CrossRef]
- Bellos, E.; Vellios, L.; Theodosiou, I.C.; Tzivanidis, C. Investigation of a solar-biomass polygeneration system. Energy Convers. Manag. 2018, 173, 283–295. [Google Scholar] [CrossRef]
- Mathkor, R.Z.; Agnew, B.; Al-Weshahi, M.A.; Latrsh, F. Exergetic Analysis of an Integrated Tri-Generation Organic Rankine Cycle. Energies 2015, 8, 8835–8856. [Google Scholar] [CrossRef]
- Zhang, Y.; Deng, S.; Zhao, L.; Ni, J.; Ma, M.; Lin, S.; Zhang, Z. Clarifying the bifurcation point on Design: A Comparative Analysis between Solar-ORC and ORC-based Solar-CCHP. Energy Procedia 2017, 142, 1119–1126. [Google Scholar] [CrossRef]
- Dabwan, Y.N.; Gang, P.; Li, J.; Gao, G.; Feng, J. Development and assessment of integrating parabolic trough collectors with gas turbine trigeneration system for producing electricity, chilled water, and freshwater. Energy 2018, 162, 364–379. [Google Scholar] [CrossRef]
- Wang, J.; Wu, J.; Xu, Z.; Li, M. Thermodynamic performance analysis of a fuel cell trigeneration system integrated with solar-assisted methanol reforming. Energy Convers. Manag. 2017, 150, 81–89. [Google Scholar] [CrossRef]
- Ozlu, S.; Dincer, I. Performance assessment of a new solar energy-based multigeneration system. Energy 2016, 112, 164–178. [Google Scholar] [CrossRef]
- Mata-Torres, C.; Escobar, R.A.; Cardemil, J.M.; Simsek, Y.; Matute, J.A. Solar polygeneration for electricity production and desalination: Case studies in Venezuela and northern Chile. Renew. Energy 2017, 101, 387–398. [Google Scholar] [CrossRef]
- F-Chart Software, Engineering Equation Solver (EES). 2015. Available online: http://www.fchart.com/ees (accessed on 15 January 2020).
- Bellos, E.; Tzivanidis, C.; Antonopoulos, K.A. Exergetic, energetic and financial evaluation of a solar driven absorption cooling system with various collector types. Appl. Therm. Eng. 2016, 102, 749–759. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 2nd ed.; John Wiley & Sons Inc.: New York, NY, USA, 1991. [Google Scholar]
- Available online: https://www.therminol.com/products/Therminol-VP1 (accessed on 15 January 2020).
- Bellos, E.; Tzivanidis, C. Performance analysis and optimization of an absorption chiller driven by nanofluid based solar flat plate collector. J. Clean. Prod. 2018, 174, 256–272. [Google Scholar] [CrossRef]
- Bellos, E.; Skaltsas, I.; Pliakos, O.; Tzivanidis, C. Energy and financial investigation of a cogeneration system based on linear Fresnel reflectors. Energy Convers. Manag. 2019, 198, 111821. [Google Scholar] [CrossRef]
- Petela, R. Exergy of undiluted thermal radiation. Sol. Energy 2003, 74, 469–488. [Google Scholar] [CrossRef]
- EU. EuroTrough II: Extension, Test and Qualification of EUROTROUGH from 4 to 6 Segments at Plataforma Solar de Almeria; Project Cooordinator: Instalaciones Inabensa, S.A. April 2003; EU: Brussels, Belgium, 2003. [Google Scholar]
- Bellos, E.; Tzivanidis, C. Assessment of linear solar concentrating technologies for Greek climate. Energy Convers. Manag. 2018, 171, 1502–1513. [Google Scholar] [CrossRef]
- Kouremenos, D.A.; Antonopoulos, K.A.; Domazakis, E.S. Solar radiation correlations for the Athens, Greece, area. Sol. Energy 1985, 35, 259–269. [Google Scholar] [CrossRef]
- Tzivanidis, C.; Bellos, E.; Antonopoulos, K.A. Energetic and financial investigation of a stand-alone solar-thermal Organic Rankine Cycle power plant. Energy Convers. Manag. 2016, 126, 421–433. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C.; Torosian, K. Energetic, exergetic and financial evaluation of a solar driven trigeneration system. Therm. Sci. Eng. Prog. 2018, 7, 99–106. [Google Scholar] [CrossRef]
- Bellos, E.; Pavlovic, S.; Stefanovic, V.; Tzivanidis, C.; Nakomcic-Smaradgakis, B.B. Parametric analysis and yearly performance of a trigeneration system driven by solar-dish collectors. Int. J. Energy Res. 2019, 43, 1534–1536. [Google Scholar] [CrossRef]















| Parameter | Value/Description |
|---|---|
| Collector type | PTC |
| Collecting area | 100 m2 |
| Storage tank volume | 4 m3 |
| Tank thermal loss coefficient | 0.5 W/m2K |
| Solar field flow rate | 2 kg/s |
| Thermal oil | Therminol VP-1 |
| Maximum oil temperature | 400 °C |
| Parameter | Value/Description |
|---|---|
| Organic Rankine Cycle (ORC) | |
| ORC working fluid | Toluene |
| Turbine isentropic efficiency | 85% |
| Power generator efficiency | 97% |
| Temperature difference in the recuperator | 10 °C |
| Pinch point in the heat recovery system | 5 °C |
| Superheating in the turbine inlet range | 0–40 °C |
| Absorption Chiller (ACH) | |
| ACH working pair | LiBr–H2O |
| ACH cooling temperature | 5 °C |
| ACH heat exchanger effectiveness | 70% |
| ACH heat rejection temperature | 40 °C |
| Vapor Compression Cycle (VCC) | |
| VCC working fluid | R290 |
| VCC heat rejection temperature | 40 °C |
| Compressor isentropic efficiency | 85% |
| VCC cooling temperature | 5 °C |
| Heating Heat Exchanger | |
| Working fluid | Therminol VP-1 |
| Heating temperature level | 60 °C |
| Parameter | Value |
|---|---|
| Nominal solar irradiation | 700 W/m2 |
| Nominal solar angle | 30° |
| Nominal ambient temperature | 25 °C |
| Yearly operating period | 2500 h |
| Parameter | Value |
|---|---|
| PTC specific cost | 250 €/m2 |
| ORC specific cost | 3000 €/kWel |
| ACH specific cost | 1000 €/kWcool |
| VCC specific cost | 300 €/kWcool |
| Storage tank specific cost | 1000 €/m3 |
| Electricity price | 0.20 €/kWh |
| Heating price | 0.10 €/kWh |
| Cooling price | 0.067 €/kWh |
| Operation and maintenance cost | 1% ∙ C0 |
| Systems | ηen | ηex | SPP | Pel | Qheat | Qcool | α | ΔTsh | Tg |
|---|---|---|---|---|---|---|---|---|---|
| (-) | (-) | (Years) | (kW) | (kW) | (kW) | (-) | (°C) | (°C) | |
| System 1 | 78.17% | 15.94% | 5.62 | 6.05 | 25.28 | 23.39 | 50.0% | 0.0 | 130 |
| System 2 | 43.30% | 13.08% | 7.82 | 6.39 | 12.42 | 11.49 | 58.8% | 27.8 | 130 |
| System 3 | 37.45% | 12.25% | 8.49 | 6.21 | 10.00 | 10.00 | 72.1% | 40.0 | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tzivanidis, C.; Bellos, E. A Comparative Study of Solar-Driven Trigeneration Systems for the Building Sector. Energies 2020, 13, 2074. https://doi.org/10.3390/en13082074
Tzivanidis C, Bellos E. A Comparative Study of Solar-Driven Trigeneration Systems for the Building Sector. Energies. 2020; 13(8):2074. https://doi.org/10.3390/en13082074
Chicago/Turabian StyleTzivanidis, Christos, and Evangelos Bellos. 2020. "A Comparative Study of Solar-Driven Trigeneration Systems for the Building Sector" Energies 13, no. 8: 2074. https://doi.org/10.3390/en13082074
APA StyleTzivanidis, C., & Bellos, E. (2020). A Comparative Study of Solar-Driven Trigeneration Systems for the Building Sector. Energies, 13(8), 2074. https://doi.org/10.3390/en13082074