Influence of the Meteorological Record Length on the Generation of Representative Weather Files ^†

Abstract

Heat and moisture (HM) transfer simulations of building envelopes and whole building energy simulations require adequate weather files. The common approach is to use weather data of reference years constructed from meteorological records. The weather record affects the capability of representing the real weather of the resulting reference years. In this paper the problem of the influence of the length of the records on the representativeness of the reference years is addressed and its effects are evaluated also for the applicative case of the moisture accumulation risk analysis with the Glaser Method and with DELPHIN 6, confirming that records shorter than 10 years could lead to less representative reference years. On the other hand, it is shown that reference years obtained from longer periods are not representative of the most recent years, which present higher dry-bulb air temperatures due to a short-term climate change effect observed in all the considered weather records. An alternative representative year (Moisture Representative Year) to be used in building energy simulations with a strong dependence on moisture is presented.

1. Introduction

Energy efficiency is an increasingly imposed requirement for new buildings and renovations. One of the possibilities to achieve low energy consumptions is to increase the thermal resistance of the external walls. Adding layers of insulation to existing building envelopes leads to lower thermal dispersion. The building energy simulation could be used to evaluate the energy savings and the effectiveness of the design choices. Depending on the application, the simulations should be performed with the appropriate weather file, usually a single year hourly series of weather variables, used to calculate the boundary conditions of a building. If the intention of the designer is to simulate the most common weather conditions, for example to evaluate the heat losses though the envelope considering also moisture transfer, a representative weather file could be used. In building energy simulations it is common practice to use the Typical Meteorological Year (TMY), defined in ISO 15927-4:2005 [1] procedure. It is designed with the application of the Finkelstein–Schafer statistical method on a meteorological record or multi-year (MY). The TMY is the result of the composition of twelve calendar months selected from the MY by the evaluation of their goodness-of-fit to the MY. To achieve a representative TMY, ISO 15927-4:2005 [1] suggests using a multi-year of 10 years or longer. This requirement could be very restrictive, for example, for the regions with only recently installed weather stations. The aim of this work is to investigate the influence of the MY length on the moisture accumulation risk assessment performed using reference years for four cities of the Northern Italy. In addition, a reference year, alternative to the TMY for the moisture related building simulations is presented.

1.1. Heat and Moisture Transfer Simulations

The simulation of the building envelope could be performed considering the coupled transfer of heat and moisture. The resulting simulation provides an accurate calculation of the heat losses, including in the calculations also the variability of the thermal material properties due to the variation of the moisture content and the temperature and the latent heat losses due to the moisture migration. These types of models have been introduced in the whole building energy simulations and their influence has been proven to be relevant in several situations. A review on the effects of an inappropriate estimation of moisture content in materials is presented in [2]. Several examples of calculation methods and tools used to perform these simulations, with different hypotheses, are presented in literature (a review of the simulation methods is presented in [3]). A comparison between the effects of using different models of heat and moisture transfer in EnergyPlus whole building simulations is presented in [4], where the models are used to compare the moisture buffering effect of the hygroscopic materials calculated with different models on the internal environmental conditions. In [5], the implementation of the heat and moisture transfer model that considers the moisture hysteresis of hygroscopic materials (described in [6] and implemented in the software MATCH) is implemented in a whole building simulation tool, BSim). Similarly, [7] presents the relevance of the implementation of the model of WUFI Pro [8] in the whole building simulation tool WUFI Plus. In addition, when the heat losses to the ground are relevant, the effects of moisture transfer could be included in the calculations with several methods (listed in [9]). Instead of considering the coupled heat and moisture transfer phenomena it is possible to study, with simplified models, only the moisture buffering of the building materials and furniture in the internal environments. This approach, presented in [10], could be used to calculate the impact of moisture migration in the building energy consumption and different models are available for this use (for example [11] or [12]). The Moisture Representative Year generation procedure presented in this work, is intended to produce representative years to be used in simulation tools that consider also the influence of rain, like the aforementioned ones. Moreover, the efficiency of some heating and cooling system components depends on the moisture content of air (for example the evaporative cooling systems [13,14], the dry cooler systems [15,16,17]) and thus, the results of the analysis would require a weather file selected also considering the weather variables related to moisture content of air. The heat and moisture transfer simulations of the walls are more frequently performed to evaluate the risks connected to the uncontrolled moisture migration. It is common, when designing the renovation of historical buildings, to add internal insulation and to be forced to limit the layer thickness due to negative results of moisture accumulation or mould growth risk assessment. The Italian legislation [18] requires the designer to assess the moisture accumulation risk by means of the national edition of standards ISO 13788:2012 [19] or EN 15026:2007 [20]. The former describes the application of the Glaser method, while the latter, defines the requirements and procedures for the advanced simulation of heat, water vapour and liquid water transfer in building materials described as porous media. In both cases, the simulations require the use of a year of weather data values as boundary conditions. For the advanced heat and moisture migration model, the hourly values of dry-bulb air temperature, water vapour pressure, global solar irradiance, wind speed, wind direction and rainfall of a reference year should be used. The reference year could be designed with the procedure described in ISO 15927-4:2005 [1], while the Glaser Method uses monthly mean values of the dry-bulb air temperature and water vapour pressure, in accordance with [21]. In both cases, the weather files should represent situations with extreme moisture loads which are often referred to as “Moisture Reference Years” in literature.

1.2. Moisture Representative Year

The TMY generation procedure is performed considering only the variables relevant to building energy simulations (rain is neglected). For this reason, an alternative reference year is proposed, the Moisture Representative Year (MRY), which is designed including the rainfall intensity and duration. For its definition, the resulting MRY has not to be considered as a critical year (as the Moisture Reference Year), but the most representative of the whole MY. Using MRY for moisture related simulations instead of critical years can lead to a valid risk indicator for non-extreme weathers and for the simulation of drying processes in which a critical reference year could lead to overestimations of the risk.

The most recent extended set of reference weather files for the Italian climate has been published by the Italian Thermotechnical Committee (CTI) in 2016, using the method reported in [22], in accordance with ISO 15927-4:2005 [1]. Further research has been carried out on the topic, extending the TMY generation methodology using on weighting coefficients, for example in [23], which provided a study on the representativeness of reference years obtained from sequentially reduced MY. Other aspects of the selection of the weather data have been investigated in a more recent study on the use weighting coefficients [24] and the effect of the different procedures of generation of representative years on the outcome of multi-objective optimization for building energy refurbishment has been studied in [25].

In literature several alternatives to the TMY have been proposed for moisture related risk assessments, designed as critical years to obtain the 10% of a given failure mode. Two alternative approaches could be used: the construction-dependent approach, based on the building features and characteristics, and the construction-independent approach, that does not depend on building characteristics and generates a reference year from the only weather data information. In [26] the construction-independent approach has been used, evaluating the considered weather files with the saturation deficit, an auxiliary parameter calculated from the climate variables, used to identify critical weather files to be used in the mould risk assessment and in the interstitial condensation risk assessment. These reference climate files could be used for the assessment of every building envelope. The construction-dependent weather file selection presented in [27], performs first a preliminary selection of three weather reference years based on the Climate Index, a construction-independent auxiliary variable, then the reference year is chosen comparing the results of the simulations of the considered building envelope. The procedure to obtain the risk assessment is more reliable, but the weather file used for the simulation could not be used for other building structures and every different risk assessment would require the computational cost of the weather selection simulations. On the other hand, few contributions provide a typical year for moisture transfer simulations. For example, [28] extended the ISO 15927-4:2005 [1] procedure to rainfall, studying the effect of the changing the set of variables used in the representative year generation, comparing the results with moisture transfer simulations on building envelopes. The MRY generation procedure presented in this work considers in addition to the rainfall intensity also an auxiliary variable, the rainfall duration, in the set of MRY primary generating variables.

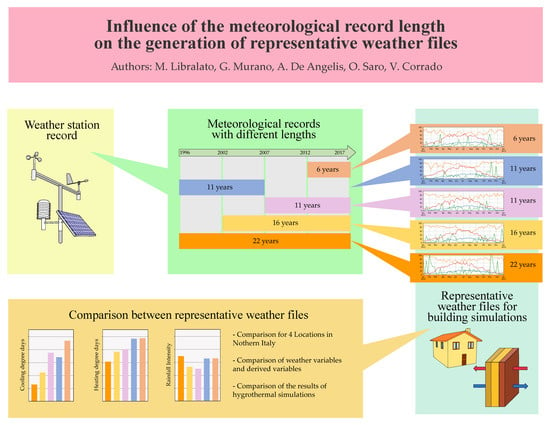
1.3. Meteorological Record Length

The boundary conditions are, along with the material properties, one of the main sources of inaccuracy of the simulations. The weather files could be chosen with the aim of representing the common climate conditions and a reference year could be used. Many Italian weather stations have produced relatively long series of measurements of dry-bulb air temperature, relative humidity, solar global irradiance and wind speed, but have only recently begun measuring rainfall and wind direction. The latter values are rarely used in building simulations, but are needed in advanced hygrothermal analysis. It is then relevant to quantify the effects of using shorter weather records for the generation of representative weather files. This aspect has been studied in [29] proving that using a different meteorological record has a relevant impact on the calculation of the heating and cooling demands of buildings in all the Italian territory.

2. Theory

The standardised methodology described by ISO 15927-4:2005 [1] applies the Finkelstein–Schafer statistic [30] on a set of primary parameters (p) which are selected as the most influential in the studied problem. The primary parameters used in ISO 15927-4:2005 for the generation of the TMY for energy building simulations are the dry-bulb air temperature (T), the global solar irradiance (I), the water vapour pressure ($\mathit{VP}$) (also the relative humidity, the air absolute humidity and the dew point temperature could be used). This set of primary variables is used to rank the MY months by representativeness using the Finkelstein–Schafer statistic. In addition, a secondary parameter is considered, the wind speed, to perform a secondary selection on the representativeness ranking and select the TMY month.

To build the MRY presented in this work, the set of primary parameters is extended including also rainfall intensity ($RI$) and rainfall duration ($RD$), two of the most influential variables in heat and moisture transfer simulations. Moreover, the secondary selection is not performed. The rainfall duration has been calculated as the number of consecutive hours with rainfall. This choice has been made to consider the fact that low intensity rainfalls with a long duration could be more influential on the moisture content of a wall than short high intensity rainfalls.

2.1. Methodology for the Construction of the MRY

For the generation of the MRY form the MY, the following procedure has been used:

(a)

Calculation the daily means $\overline{p}$ of the primary variables p for the whole MY.

(b)

Calculation of the cumulative distribution function $\mathsf{\Phi }(p,m(i),i)$ of the daily means $\overline{p}$ over the whole MY for each day i of a selected calendar month m, for each p. The variable i represents the ordered number of a day in the MY, from 1 to N (number of days in the MY), and it will be used as a time-stamp. The function $\mathsf{\Phi }$ is obtained from the ranking $K(\overline{p},m,i)$ by numbering the values of the distributions of the considered p, separately for each m:

$$\mathsf{\Phi }(p,m\left(i\right),i)=\frac{K(\overline{p},m\left(i\right),i)}{N+1}$$

(1)

(c)

Calculation of the cumulative distribution function of the daily means within each calendar month m of each year y, $F(p,y(i),m(i),i)$ from the rank order $J(\overline{p},m\left(i\right),i)$, obtained ordering the daily means $\overline{p}$ within the calendar month m and the year y:

$$F(p,m\left(i\right),i)=\frac{J(\overline{p},y\left(i\right),m\left(i\right),i)}{n+1}$$

(2)

where n is the number of days of the m calendar month considered.

(d)

The Finkelstein–Schafer statistic is calculated for each p and each calendar month m in the MY as:

$$F_S(p,y,m)=\sum _{i=1}^n|F(p,y\left(i\right),m\left(i\right),i)-\mathsf{\Phi }(p,m\left(i\right),i|$$

(3)

(e)

For each p, the ranking R is assigned to each calendar month m, obtained from the ordering of the $F_S(p,y,m)$ of each y separately for each calendar month m:

$$R(p,y,m)=\frac{L\left(F_S\right)}{n_y+1}$$

(4)

with $n_y$ the number of years of the MY.

(e)

The ranking R of each calendar month is calculated for all the primary parameters and then summed, to obtain the total ranking $R_{tot}$:

$$R_{tot}(y,m)=R(T,y,m)+R(VP,y,m)+R(I,y,m)+R(RI,y,m)+R(RD,y,m)$$

(5)

(e)

Each calendar month m of the MRY is chosen among the months of the MY as the month m of the year y with the lowest $R_{tot}$.

(e)

The MRY is composed by the hourly series of the weather variables of the selected months and the continuity between every month is set with a linear interpolation, in order to provide a smooth transition between months from different years.

2.2. Rainfall Duration

As seen at the step (a) of the MRY design procedure, the weather variables are not considered as hourly values, but as daily means, losing some information about the distribution in time of the variable. With this calculation, a rain event of two consecutive hours is not distinguishable from two separate rain events of the same overall intensity, while the difference between the two effects on the analysed wall is different. For this reason, the auxiliary variable $RD$, rainfall duration, has been introduced in the set of primary parameters.

3. Materials and Methods

The MYs measured by four weather stations of Northern Italy have been considered, the cities and the weather stations locations are listed in

Table 1. Positions of the considered weather station and length of the multi-year record.

Station	Lat.	Long.	Alt.	MY Years
	(${}^{°}$)	(${}^{°}$)	(m a.s.l.)
Aosta—Saint-Christophe	45.75	7.68	569	1996–2017
Bergamo—via Stezzano	45.66	9.66	211	1996–2017
Torino—Loc. Bauducchi	44.96	7.71	226	2002–2017
Udine—S. Osvaldo	46.03	13.23	91	1996–2017

. The MRY and TMY have been designed for every station, considering, when possible, 5 different MY lengths: 1996–2017, 1996–2006, 2002–2017, 2007–2017, 2012–2017. The obtained weather files are compared among them evaluating their representativeness of the full weather record and of the last 6 years of the weather record. A further investigation has been performed comparing the results of the moisture accumulation risk analysis on six different walls, obtaining an auxiliary analysis that considers both heat and moisture related weather variables.

3.1. Weather Data Set

The weather data set presented short periods (shorter than two days and of the 10% of the hours of each month) of missing and invalid values (relative humidity higher than 1 or positive global solar irradiance at night). They have been replaced with different interpolation techniques, depending on the duration of the missing data. The missing data of the wind speed for the period from the 1996 to 2011 for the station of Bergamo (rural area—station of via Stezzano) have been substituted with the scaled wind speed measurements of another weather station of Bergamo (urban area—station of via Garibaldi). To normalize the wind speed values of the measurements of the second weather station, they have been scaled of a factor equal to the rate between the means of the wind speed in the two locations. Due to an excessive lack of data, the wind direction measurements for the city of Bergamo have not been considered.

Figure 1 shows the rainfall intensity annual means of the MY of the four stations and the rainfall duration annual mean, calculated as the sum of the annual hours of rain divided by the number of hours of the year. The two plots, even if the two variables are different, show a similar behaviour, with some exceptions. These are due to high intensity rainfalls with a duration of less than an hour, that could be less influential on the moisture content of building materials than long-lasting low intensity rains. In order to give more relevance in the representative year construction process, the rainfall duration has been included as a primary parameter.

In Figure 2a, the annual mean rainfall intensity in Udine is presented. The values are calculated as the total rainfall of the year divided by the number of hours of the year. The relatively large standard deviation shows that the $RI$ has a large variability compared to the one of the other variables.

For example, the air dry-bulb temperature plot in Figure 2b shows a relatively small standard deviation, indicating less extreme values and a more regular trend. Similar behaviours have been observed for the other stations. The effect of this behaviour is reflected in Figure 3, where the distribution of the monthly mean values of the variables of each month of the MY are plotted separately. The distributions of the dry-bulb air temperature (Figure 3a) have regular values, relatively closer to the MY median, while the rainfall intensity has relatively larger variations from the MY median and more extreme values (indicated by the circles). The Finkelstein–Schafer statistic is applied on a monthly basis, on the temperature and the rain intensity (among the other variables) distributions but, due to the different distributions, it has a different effectiveness. As a result, the annual mean values of rain intensity are not similar to the ones of the multi-year, while, on the contrary, the dry-bulb air temperature is well represented.

It is interesting to note that the variables depending to the temperature tend to increase along the weather record. For the case of Udine, in Figure 2b it is shown that the air dry-bulb temperature trend line increases of $0.06$ ${}^{°}\mathrm{C}$ every year (with similar trends for the other locations: Aosta $0.05$ ${}^{°}\mathrm{C}$, Bergamo $0.09$ ${}^{°}\mathrm{C}$, Torino $0.03$ ${}^{°}\mathrm{C}$). The accumulated temperature differences, hereafter referenced as degree days, are calculated (according the standard UNI 10349-3:2016 [31]) for the four locations, considering the heating and cooling base temperatures $T_b$. The heating degree days ($HDD$) are calculated according Equation (6), while the cooling degree days ($CDD$) are calculated according to Equation (8).

$$HDD=\sum _{h=1}^n\frac{\Delta T_{H,h}}{24}$$

(6)

with

$$\Delta T_{H,h}=\left\{\begin{array}{cc}{T}_h-T_b\hfill & \mathrm{if}{T}_h-T_b>0\hfill \\ 0\hfill & \mathrm{else}\hfill \end{array}\right.$$

(7)

$$CDD=\sum _{h=1}^n\frac{\Delta T_{C,h}}{24}$$

(8)

with

$$\Delta T_{C,h}=\left\{\begin{array}{cc}{T}_b-T_h\hfill & \mathrm{if}{T}_b-T_h>0\hfill \\ 0\hfill & \mathrm{else}\hfill \end{array}\right.$$

(9)

where:

• n is the total number of hours in the considered year
• $T_h$ is the air dry-bulb temperature at hour h
• $T_b$ is the base temperature, set to 20 ${}^{°}\mathrm{C}$ for the heating period and to 26 ${}^{°}\mathrm{C}$ for the cooling period
• $\Delta T_{H,h}$ is the positive temperature difference for the $HDD$ calculation
• $\Delta T_{C,h}$ is the positive temperature difference for the $CDD$ calculation

The values calculated for Udine are plotted in Figure 4. It is observed that the $HDD$ are decreasing with a trend of −11.83 degree days each year, meaning that the winter temperatures are, in average, higher in the last years of the weather record. This trend will affect the building energy simulations, resulting in lower heating demands. When considering the moisture related weather variables, it is observed that the trend of the rainfall intensity is constant for Udine (Figure 3). This trend is found also for the other considered locations and will result in higher cooling demands in building energy simulations.

To study the air moisture content, it is possible to consider the humidity ratio x and the saturation deficit ${\delta }_s$. The saturation deficit is calculated as the difference between the humidity ratio at saturation condition at air temperature and the actual humidity ratio, as in Equation (10).

$${\delta }_s=x_{sat}\left(T\right)-x$$

(10)

The saturation deficit is a variable that could be used to identify the drying potential of the humid air. In the plots in Figure 5, the annual mean saturation deficit and the annual mean humidity ratio are plotted for the weather record of Udine. The humidity ratio has a growing trend of 0.06 g${}_{\mathrm{w}}$/kg${}_{\mathrm{d}}$ per year in Udine, while for the other locations similar values are obtained (Aosta 0.02, Bergamo 0.01, Torino 0.05 g${}_{\mathrm{w}}$/kg${}_{\mathrm{d}}$). On the other hand, the saturation deficit, that depends also on temperature, shows different trends among the stations, with positive or negative trends. In Figure 5 the annual average saturation deficit for Udine are presented. The trend is decreasing by 0.01 g${}_{\mathrm{w}}$/kg${}_{\mathrm{d}}$ every year. The other stations have positive (Aosta: 0.03, Bergamo 0.06 g${}_{\mathrm{w}}$/kg${}_{\mathrm{d}}$) per year and negative trends (Torino −0.02 g${}_{\mathrm{w}}$/kg${}_{\mathrm{d}}$ per year).

All the presented trends show a variation in the years of the weather record and that will prevent the generated years to be representative of the future years, or at least of the last and warmer years of the record. The mean values of the considered weather variables for the whole weather record are presented in

Table 2. Mean values of the weather variables for the whole weather records.

Station	T	x	${\mathit{\delta }}_{\mathit{s}}$	$\mathbf{HDD}$	$\mathbf{CDD}$	$\mathbf{RI}$
	(${}^{°}\mathbf{C}$)	(g${}_{\mathbf{w}}$/kg${}_{\mathbf{d}}$)	(g${}_{\mathbf{w}}$/kg${}_{\mathbf{d}}$)	(Degree Days)	(Degree Days)	(mm/year)
Aosta	11	5.3	4.6	3493	66	563
Bergamo	13	7.5	3.6	2813	94	1173
Torino	13	7.4	3.4	3099	102	757
Udine	13	7.6	3.4	2760	83	1485

and the mean values of the last 6 years of the weather record are shown in

Table 3. Mean values of the weather variables for the last 6 years of the weather records.

Station	T	x	${\mathit{\delta }}_{\mathit{s}}$	$\mathbf{HDD}$	$\mathbf{CDD}$	$\mathbf{RI}$
	(${}^{°}\mathbf{C}$)	(g${}_{\mathbf{w}}$/kg${}_{\mathbf{d}}$)	(g${}_{\mathbf{w}}$/kg${}_{\mathbf{d}}$)	(Degree Days)	(Degree Days)	(mm/year)
Aosta	12	5.6	4.7	3378	101	454
Bergamo	14	7.4	4.5	2629	141	1181
Torino	13	7.7	3.4	3066	122	590
Udine	14	8.1	3.9	2656	106	1400

. It is observed that the last years have higher values of weather variables related to the heat balance calculation than the whole weather record.

3.2. Representative Years Evaluation Method

The representative years produced in this study have been evaluated first comparing the average values of some weather parameters and then, in order to obtain a synthetic comparison parameter they have been used in a moisture accumulation risk assessment. The average weather variables of the representative years have been compared first with the average of the whole weather record, then with the last 6 years of the record, in order to evaluate if the generated years could be representative of the most recent years, or if they are representative of the past years.

The evaluation of the moisture content has been performed using a simplified method, the Glaser Method and an advanced model, using the software DELPHIN 6 [32]. The first method considers the air dry-bulb temperature and the relative humidity, while the advanced model considers also the rainfall intensity, solar global irradiance and, if required, the wind speed and direction for the calculation of the driving rain. For the sake of simplicity, in this evaluation, the wind speed and direction have not been used, and the whole rainfall intensity has been considered as driving rain on the wall. This unrealistic hypothesis is taken for the purpose of the comparison, in order not to distinguish between different orientations and to evaluate the representativeness of the generated years with higher moisture contents variations. Considering also the wall orientation should be also considered in the representative year generation procedure, considering the driving rain intensity on the wall, instead of the normal rainfall intensity. This choice would lead to a structure-dependent weather file. The evaluation of the risk parameter has been performed with a simplified method for both simulation procedures. The risk $P_y^G$ for the Glaser method (G) over the period y has been calculated evaluating the ratio between $n_{m|\phi =1}$, number of months with the relative humidity equal to 1 and the total number of months $N_m$ of y as in Equation (11).

$$P_y^G=\frac{n_{m|\phi =1}}{N_m}$$

(11)

The evaluation for the MY has been performed considering all the monthly mean variables for all the months of the MY, while, the assessment for the representative years has been performed for a period of five years. The assessment of the risk $P_y^D$ for the advanced simulation method has been performed using the same number of years. Five years is the time required in the DELPHIN 6 simulations for the total moisture content of the wall at the first time-step of the year to be equivalent to the moisture content of the first time-step of the following year. The risk $P_y^D$ has been calculated as the ratio between $n_{h|\phi =0.95}$, number of hours with values of relative humidity higher than $0.95$ on an internal layer of the wall, and $N_h$, the total number of hours considered in the simulation (Equation (12)).

$$P_y^D=\frac{n_{h|\phi =0.95}}{N_h}$$

(12)

The external layer has not been considered for this evaluation. The indoor and outdoor surface boundary conditions for the DELPHIN 6 simulations are set in accordance with [20], the internal environment is set to the “normal occupancy” conditions described in the standard. The Glaser method boundary conditions are set in accordance with [19], for a continental climate with normal occupancy. The material properties are taken from the DELPHIN 6 material database. In both approaches the internal surface thermal resistance is set to 0.25 m${}^2·$K/W and the external surface thermal resistance to 0.04 m${}^2·$K/W. In the DELPHIN 6 simulations the surface vapour exchange equivalent air layer thickness is set to 0.003 m on the outside and to 0.008 m on the inside. For both simulation procedures, a risk of 0 indicates that the water condensation has never occurred, while a risk equal to 1, denotes the presence of liquid water in a layer of the wall in every time-step of the simulation period. The risk assessment has been performed for six walls, typical of the Northern Italy regions [33], redesigned to have liquid water condensation and accumulation between the material layers. The walls are described in Figure 6. The wall properties are summarized in

Table 4. Description of the considered walls. The variables presented in the table are wall thickness d, thermal transmittance U and equivalent air layer thickness for the vapour diffusion $S_d$ of the walls considered for the risk assessment evaluations. The walls are identified in Figure 6.

Wall	Id.	d	U	${\mathit{S}}_{\mathit{d}}$
		(m)	(W/m${}^2$K)	(m)
Stone wall	SW	0.38	0.70	5
Well insulated stone wall	SWi	0.53	0.13	50
Hollow brick wall	HB	0.49	0.39	7
Well insulated hollow brick wall	HBi	0.58	0.15	41
Timber wall with internal vapour barrier	TWa	0.53	0.13	56
Timber wall with external vapour barrier	TWb	0.53	0.13	56

.

4. Results

To evaluate the representative years that have been generated, a comparison of the weather variable mean values is presented. The Finkelstein–Schafer statistic compares the distribution of different weather variables of the multi-year and excludes the months with extreme values with the ranking procedure in both representative year generation methods. Therefore, the MRY and TMY generated from the five different MY should have mean values of the weather variables similar to the ones of their own reduced MY, and could be different from the ones of the whole MY. This behaviour is shown for all the studied locations in Figure 7 and Figure 8. Figure 7 shows the distribution of the values of the dry-bulb air temperature with a box-plot. With this representation it is possible to observe the extreme values of the hourly distribution. The representative years have higher minimum temperatures and lower maximum temperatures (confirming that the Finkelstein–Schafer statistic excludes the extreme values even for periods shorter than 10 years) and that the median values and the 25th and the 75th percentile are higher for the representative years obtained from the more recent MY (2007–2017 and 2012–2017).

On the other hand, in some cases, the minimum and maximum temperatures are required to choose heating and cooling devices and, in absence of these values, it is possible to use the reference year values with an appropriate correction. Figure 7 shows that the extreme temperatures of MRY and TMY generally increase for the less recent MY, while not being as extreme as the ones of the MY. This could influence the choice of the devices. In all the figures, the mean values of the weather variables calculated from the generated years are presented with the average values of the whole multi-year record (MY) and the average values of the last 6 years of the MY. The average values of the MRYs are highlighted with a blue background, the TMYs have a red background while the MY values have a white background. The values of the 6 year long MY record are presented to represent the last years of the MY that have higher dry-bulb air temperatures due to a short-term climate change effect that affected all the locations. This comparison is meant to highlight the difference between the representative years obtained with longer MY records and the ones obtained with the last 6 years of the MY records. It has been observed that the representative years obtained with the longer MY and despite being considered more representative of a weather of a location, they are less representative of the last years of the MY (and supposedly of the future climate).

The heating degree days ($HDD$) and cooling degree days ($CDD$), calculated according Equations (6) and (8), are here considered to evaluate the representativeness of the generated years as weather files from the energy point of view, for the applications in building energy simulations. $HDD$ and $CDD$ have been often used in literature as an indicator for the classification of locations from the point of view of the building energy demands, and it has also been used to identify a correlation between the energy demands of non-residential buildings and the locations [34]. On the other hand, the saturation deficit and the rainfall intensity (that are commonly used in literature, also with combinations of the two, to characterise weather files [26,27]), are considered to evaluate the representativeness of the generated weather files from the point of view of the moisture related applications and the use in HM transfer simulations.

In Figure 8a it is observed that the $HDD$ for the MRY is larger than the $HDD$ of the TMY, and that the TMY are closer to the MY values. This result could be due to the introduction of two new weather variables (rainfall intensity and duration) in the month selection procedure, that could reduce the representativeness of the other variables (including temperature). The MRY and the TMY obtained from the 1996–2017 MY have larger $HDD$ values for all the considered locations, meaning that the generated years have colder winters. Similarly, the years generated from the MY 2007–2017 and MY 2012–2017 show warmer temperatures, with values similar to the 6 year MY mean $HDD$ values. This comparison is intended to show that the years generated with the larger MY could be less representative of the last part of the MY when the last years have higher temperatures and could cause lower heating energy demands. As a result, for the shown cases, the MRY and TMY obtained from the MY 1996–2017 are less representative of the last 6 years of the MY, than the years generated from the 6 years MY.

A similar behaviour is shown in Figure 8b. In this case, lower values of the $CDD$ are the result of lower temperatures during the cooling season, while the positive values indicate that the representative year has higher temperatures that could cause higher cooling energy demands. It is shown that generally, the year generated from the whole MY have lower $CDD$ values and could be correlated to lower cooling energy demands, while the ones obtained from the last 6 years have relevantly higher $CDD$ values. Comparing the representative files to the 6 years MY it is observed that, generally, the ones obtained from the MY that contain the years before the 2007 are considerably less representative. When considering the saturation deficit in Figure 8d, a trend is not evident. For Bergamo it is observed that the saturation deficit is larger for the years generated with the most recent MY, while the other locations are well represented by the generated years.

In Figure 8c the total annual rainfall intensity is represented for the generated years. As shown in Figure 3, the rain intensity has a different distribution which could not be easily represented by a month selection made using the Finkelstein–Schafer statistic. Given the differences between the registered rainfall intensity series of each month, the selected representative month will easily have different rainfall intensity mean values, resulting in reference years with annual total rainfall values different from each other and from the MY. This could also explain the absence of a visible trend in the representative years. The rainfall intensity values of the generated years are generally in accordance with the average values of the MY, with some extreme values. These are observed for the location of Aosta for the MRY 02-17 and 07-17 and for the generated years of Torino. The average values of the TMY 02-17 and the TMY 96-06 in Bergamo are lower than the MY averages.

Risk Analysis

The results of the evaluation based on the moisture accumulation risk analysis performed with the software DELPHIN 6 and with the Glaser method are presented in Figure 9 and Figure 10. The values presented in the plots are differences $\Delta P^I$ (defined in Equation (13)) between the risk $P_{RY}^I$ calculated with the use of a representative year (specified on the x axis) and the risk $P_{MY}^I$, obtained using the MY from the year as boundary conditions. In order to be representative, the generated years should provide interstitial condensation risk values close to the ones obtained with the MY. Larger $\Delta P^I$ values indicate less representative generated years. The superscript I indicates the calculation method used: G for the Glaser method and D for the DELPHIN 6 simulation.

$$\Delta P^I=P_{RY}^I-P_{MY}^I$$

(13)

The MY for the stations of Aosta, Bergamo and Udine is from the year 1996 to 2017, while the one for Torino is form the 2002 to 2017. Positive values of $\Delta P^I$ indicate higher $P_{RY}^I$ values, meaning that the representative year simulation is conservative.

The DELPHIN 6 simulations performed using the representative years are generally in accordance with the MY simulations. The exceptions are visible in the plot for the station of Aosta in Figure 9, where the MRY obtained with the records 1996–2017, 2002–2018, 2007–2017 of the station of Aosta produce over-conservative results for the HB, HBi, SWi walls (the wall identifiers are listed in Figure 6). The representative years obtained from the station of Bergamo are generally in accordance with the MY simulations except for the not acceptable underestimations given by the MRY from the records 1996–2006, 2002–2007 and 2012–2017 and the TMY from the 2002–2017 and 2012–2017. For the station of Torino the results of the representative years are generally in accordance with the MY risks with the exception of the MRY 2012–2017 that underestimates the risk. The MRY 2002–2017 and 2007–2017 and the TMY 2007–2017 are overestimating the risk in a relevant manner for the SWi wall. The results of the generated years for the station of Udine are generally conservative respect to the MY. The most representative results are given by the MRY 1996–2017 and by the TMY 1996–2006. The Glaser method results, presented in Figure 10, denote a general good agreement between the generated years and the MY, for every station. The results for the station of Bergamo are slightly underestimating the risk of moisture accumulation for each generated year, with peaks at the generated years of the period 2012–2017.

5. Conclusions

The influence of the meteorological record length for the generation of weather files of reference years has been evaluated for the moisture accumulation risk assessment for four weather stations in Northern Italy: Aosta, Bergamo, Torino and Udine. Five sets of years have been considered as MY for the representative years generation: 1996–2017, 1996–2006, 2002–2017, 2007–2017, 2012–2017. Two representative years construction method have been considered, the TMY used for building energy simulations, defined in ISO 15927-4:2005 [1], and the MRY, proposed in this work, to be used in heat and moisture transport simulations. It has been found that the TMY and the MRY generation procedures generate years representative of the considered MY and the representativeness has been evaluated observing the effects of the warming of the weather in the considered locations. Afterwards, ten representative years produced for every station have been used for the moisture accumulation risk assessment of six walls with two methods: the Glaser method and with the software DELPHIN 6. The risks calculated using the MRY and TMY have been compared with the risks obtained from the full MY. It has been observed that, as a general trend, the MRY and TMY obtained from the full MY produced the most representative results, while the MRY and TMY from the shorter MY intervals resulted to be less representative. In some cases, the generated years obtained from periods shorter than 10 years could be less representative and lead to underestimations of the risks. When the risk is assessed using the Glaser method the differences of risk are less than 0.25, while for the walls with thicker layers of insulation, the risk differences calculated with DELPHIN 6 are from 0.5 to 0.75. When the moisture content is evaluated with HM models and the rain is considered as a moisture source in the calculation, and larger variations of moisture contents could be expected, with larger differences between the resulting risks evaluated. Finally, from these results it could be concluded that the proposed MRY construction method leads to valid representative years that could be used for moisture related calculations in addition to critical years, as representations of the long term mean weather data, for moisture accumulation risk analysis or simulations of drying of building structures. On the other hand, the weather files generated from the full multi-year have been observed to be less representative of the recent years (and supposedly of the future years), due to the warming trends observed in the meteorological records. Future work will concentrate on further evaluations of the presented MRY generation procedure for different climate zones, considering the warming effects of the multi-year weather series. Even if [29] found similar results for all the Italian territory, it is not possible to extend the validity of the results to other climate zones and further evaluations are required. The findings suggest that also other designing procedures of building systems could be influenced by these differences (considering also the extreme temperatures variations). Among the others, the systems whose efficiency depends on weather conditions should be studied, for example heat pumps [35,36,37], evaporative cooling systems [13,14] or dry coolers [15,16,17] systems, that are relevant for large scale planning, energy savings, water and carbon footprint reduction [38,39].