A Reference Thermal-Hydrologic-Mechanical Native State Model of the Utah FORGE Enhanced Geothermal Site

Abstract

The Frontier Observatory for Research in Geothermal Energy (FORGE) site is a multi-year initiative funded by the U.S. Department of Energy for enhanced geothermal system research and development. The site is located on the margin of the Great Basin near the town of Milford, Utah. Work has so far resulted in the compilation of a large amount of subsurface data which have been used to improve the geologic understanding of the site. Based on the compiled data, a three-dimensional geologic model describing the structure, composition, permeability, and temperature at the Utah FORGE site was developed. A deep exploratory well (Well 58-32) and numerous tests conducted therein provide information on reservoir rock type, temperature, stress, permeability, etc. Modeling and simulation will play a critical role at the site and need to be considered as a general scientific discovery tool to elucidate the behavior of enhanced geothermal systems and as a deterministic (or stochastic) tool to plan and predict specific activities. This paper will present the development of a reference native state model and the calibration of the model to the reservoir pressure, temperature, and stress measured in Well 58-32.

1. Introduction

Extracting heat from hot crystalline basement rocks through an artificially engineered reservoir is a concept that dates back many decades [1,2], first being described as a hot dry rock (HDR) system and originating from the Los Alamos National Laboratory (LANL) in the 1970s [3]. In these early experiments, the permeability of existing natural fractures was enhanced by hydraulic stimulation, rather than increasing the bulk rock permeability by creating new fractures [4,5,6]. Accordingly, the term enhanced (or engineered) geothermal systems (EGS) is now more widely used and accepted.

The development of EGS has the potential to dramatically increase the deployment of geothermal resources in the U.S. and around the world [7,8,9]. EGS resources are far more abundant and widespread than conventional geothermal systems but require advances in drilling, characterization, monitoring, and reservoir creation technologies to enable EGS resources to be commercially viable.

The U.S. Department of Energy’s Geothermal Technologies Office (GTO) has launched a series of research initiatives to accelerate the development of EGS technologies. The Frontier Observatory for Research in Geothermal Energy (FORGE) is one such initiative. The FORGE site is located inside the southeast margin of the Great Basin near the town of Milford, Utah (Figure 1 and Figure 2). The FORGE initiative consisted of three phases, which can be generally described as initial site selection (Phase 1), site characterization and down-selection (Phase 2), and site establishment and operations (Phase 3). The work and results discussed in this paper are inclusive of all Phase 1 and Phase 2 efforts at the Utah FORGE site.

The work through the end of Phase 2 at the Utah FORGE site resulted in the compilation of a large amount of new and legacy data within and surrounding the project site, incorporating information for Roosevelt Hot Springs, the central segment of the Mineral Mountains, and most of the north Milford valley. Results from the deep subsurface characterization were used to further improve the geologic understanding of the site. Site characterization is described in detail in the Utah FORGE Phase 2 report [11]. Based on the compiled data, a three-dimensional (3D) geologic model describing the structure, composition, permeability, and temperature at the Utah FORGE site was developed [11,12].

1.1. Overview of the Geologic Model

The Utah FORGE site is located near the southeast margin of the Great Basin. The regional stratigraphy is made of folded and imbricated Paleozoic-Mesozoic strata that have been overprinted by a widespread Basin and Range style extension and eruption of Tertiary-recent mafic-felsic magmatic centers [10,13,14]. Near the Utah FORGE site, Paleozoic-Mesozoic strata are absent, and consequently the stratigraphy is divided into two units composed of (1) crystalline plutonic rocks that form the basement (“granitoids”) and (2) younger overlying bedded alluvium and volcanic deposits that fill the basin (“basin fill”). The processing of a 3D seismic reflection highlights the westward-dipping surface that separates these two units, which forms the basement contact.

The basement rocks were emplaced between 26 and 8 Ma [14], and young rhyolite centers (0.5–0.8 Ma) in the Mineral Mountains [15] were the most recent eruptions. Tightly folded Precambrian gneiss ($\approx 1720$ Ma) was intruded by the granitoid plutions, but only small amounts of these older rocks are preserved in parts of the Mineral Mountains.

The basin fill consists of a thick sequence of interlayered sedimentary and volcanic deposits (>3000 m), ranging in age from Tertiary to recent. The strata from oldest to youngest consist of localized flows of andesitic lavas, tuffaceous deposits, volcaniclastic sandstones and gravels, and calcareous lacustrine siltstones and sandstones. In the area surrounding the FORGE site, alluvial fans are largely composed of materials derived from the Mineral Mountain, including scattered fragments of obsidian and pea-sized gruss. The oldest alluvium may be several million years old, being restricted to a few isolated exposures [10,16].

As part of the FORGE Phase 2 activities, the Utah FORGE team developed a comprehensive earth model of the Milford Site and surrounding area. The key outcome from the earth modeling, in addition to incorporating the geologic, geophysical, geochemical data, etc., was the establishment of a “reference” earth model for use by numerical modelers to ensure that consistent geologic structural features and reservoir parameters could be used in numerical simulations. All the data used to create the reference earth model are also available on the National Geothermal Data System [17,18,19,20,21] and the Utah FORGE website. Note that all earth modeling data uses SI units in UTM, Zone 12N, NAD83, and NAVD88 referenced coordinates.

1.2. Modeling and Simulation Overview

Multiphysics reservoir models have been developed to simulate the coupled thermo-hydro-mechanical responses in the subsurface to FORGE reservoir creation and operation activities. The numerical reservoir models are based on the reference geologic model discussed above and will be used as a tool to better understand the physics of the reservoir-creation process and to elucidate the behavior of the system. Numerical implementation of the conceptual model has been made with both commercial software packages and open-source numerical packages to enable greater collaboration among the team (and the geologic community) and to drive understanding of the system using state-of-the-art tools. The modeling and simulation team used these models to preliminarily evaluate drilling directions and injection pressures to both stimulate existing fractures and generate new ones for potential FORGE operational wells.

Continuum-based modeling codes are by far the most prevalent in geothermal reservoir engineering. Solution schemes based on finite-difference, finite-element, or finite-volume methods all represent the subsurface as a generalized representative elementary volume, at various grid scales, to simulate and predict behavior. In densely fractured formations, it is common to use a discrete fracture network (DFN) as a starting point to develop upscaling relationships in the development of continuum models. For Utah FORGE, the project team has established a reference DFN using FracMan [22] and a reference native state model using the FALCON code [23,24].

1.2.1. FracMan

Golder’s FracMan code (Redmond, WA, USA) is commercially available DFN software and can be used to capture the anisotropy and connectivity of a natural fracture system. The fracture system in the rock mass can be explicitly modeled by building 3D networks of stochastically generated smaller fractures and also deterministically mapped larger structures. Fracture models can be calibrated against well log information, outcrops, well test data, and seismic data. The fracture models can be used for rock mechanics analyses (such as critical stress analysis) and fluid-flow modeling. Multiple stochastic realizations can be generated and used for uncertainty quantification through Monte Carlo simulation and analysis. The DFN model can also be upscaled into equivalent grid properties on structured meshes, providing volume averaged fracture rock mass properties such as permeability and porosity.

1.2.2. FALCON

FALCON (Fracturing And Liquid CONvection [23,25]) is a multipurpose subsurface simulator for coupled thermal-hydraulic-mechanical-chemical (THMC) problems and has been used for the study of geothermal reservoir dynamics, groundwater flow and transport, carbon sequestration, etc. The code was developed using Idaho National Laboratory’s (INL) Multiphysics Object-Oriented Simulation Environment (MOOSE) framework [26,27]. The architecture that FALCON inherits from MOOSE has a plug-and-play modular design structure based on representing the governing partial differential equations (PDEs) in a weak form, with the residual term being described as a “kernel.” Kernels are solved using a finite element scheme and may be coupled together to achieve different application goals. The architecture of MOOSE allows convenient coupling of different processes.

FALCON has been validated through a number of benchmark problems [24]; the source code is open source and can be downloaded here. While it is beyond the scope of this manuscript to discuss the governing equations in great detail (see references cited above, or the MOOSE documentation page for full details), the discussion that follows provides a summary of the governing equations.

Mass Conservation. The continuity equation is used to describe the mass conservation for fluid species $\kappa$:

$$0=\frac{\partial M^{\kappa }}{\partial t}+M^{\kappa }\nabla ·{\mathbf{v}}_s+\nabla ·{\mathbf{F}}^{\kappa }+\Lambda M^{\kappa }-\varphi I\mathrm{chem}-q^{\kappa }.$$

(1)

Here, M is the mass of fluid per bulk volume (measured in kg m${}^{-3}$), ${\mathbf{v}}_s$ is the velocity of the porous solid skeleton (measured in m s${}^{-1}$), $\mathbf{F}$ is the flux (a vector, measured kg s${}^{-1}$ m${}^{-2}$), $\Lambda$ is a radioactive decay rate, $\varphi I\mathrm{chem}$ represents chemical precipitation or dissolution, and q is a source (measured in kg m${}^{-3}$ s${}^{-1}$). The coupling between mass flow and solid mechanics is via the $M\nabla ·{\mathbf{v}}_s$ term, as well as through changes in porosity and permeability. Heat flow and chemical reactions are coupled to mass conservation using the equations of state used in the terms of Equation (1), as well as the source term $q^{\kappa }$. The species are identified by $\kappa =1,\dots$.

Mass Density. The mass of species $\kappa$ per a given volume of rock is written as the sum over all phases that are present in the system:

$$M^{\kappa }=\varphi \sum _{\beta }{S}_{\beta }{\rho }_{\beta }{\chi }_{\beta }^{\kappa }(1-\varphi )C^{\kappa }$$

(2)

The solid’s porosity is $\varphi$. $S_{\beta }$ is the saturation of phase $\beta$ (liquid, gas, etc.). The density of phase $\beta$ is written as ${\rho }_{\beta }$. The mass fraction of a component $\kappa$ present in phase $\beta$ is ${\chi }_{\beta }^{\kappa }$. The term $C^{\kappa }$ is the mass of absorbed species per volume of solid rock-grain material into the porous rock matrix. The density ${\rho }_{\beta }$ is a function of pressure and temperature based on the equation of state.

Flux. The sum of the advective flux and diffusive-and-dispersive flux is referred to collectively as flux in our formulation:

$${\mathbf{F}}^{\kappa }=\sum _{\beta }{\chi }_{\beta }^{\kappa }{\mathbf{F}}_{\beta }^{\mathrm{advective}}+{\mathbf{F}}_{\mathrm{diffusion}+\mathrm{dispersion}}^{\kappa }$$

(3)

Advective flux is described using Darcy’s law. Each phase present is assumed to obey Darcy’s law; they each have their own density ${\rho }_{\beta }$, relative permeability $k_{\mathrm{r},\beta }$, viscosity ${\mu }_{\beta }$, and pressure $P_{\beta }$. Using these, we represent the advective Darcy flux as

$$\mathbf{F}{\beta }^{\mathrm{advective}}={\rho }_{\beta }{\mathbf{v}}_{\beta }=-{\rho }_{\beta }\frac{{kk}_{\mathrm{r},\beta }}{{\mu }_{\beta }}(\nabla P_{\beta }-{\rho }_{\beta }\mathbf{g})$$

(4)

In this equation ${\mathbf{v}}_{\beta }$ is the Darcy velocity (volume flux, measured in m·s${}^{-1}$) in phase $\beta$. It is used below in the diffusive-and-dispersion flux, too. The absolute permeability is denoted by k, and it is a tensor. The relative permeability of phase $\beta$ is denoted by $k_{\mathrm{r},\beta }$. It is always a function of the saturation(s), but with Klinkenberg effects, it may also be a function of the gas pressure. Relative permeability can also be hysteretic, so that it depends on the history of saturation.

Heat Transport. The continuity equation for heat is used to describe energy conservation:

$$0=\frac{\partial \mathcal{E}}{\partial t}+\mathcal{E}\nabla ·{\mathbf{v}}_s+\nabla ·{\mathbf{F}}^T-\nu (1-\varphi ){\sigma }_{ij}^{\mathrm{eff}}\frac{\partial }{\partial t}{ϵ}_{ij}^{\mathrm{plastic}}{q}^T$$

(5)

where $\mathcal{E}$ is the heat energy per unit volume, ${\mathbf{v}}_s$ is velocity of the porous solid skeleton, ${\mathbf{F}}^T$ is the heat flux, $\nu$ provides the ratio of energy from plastic-deformation that is transferred to energy in the form of heat, ${\sigma }_{ij}^{\mathrm{eff}}$ is the effective stress (see Equation (7)), ${ϵ}_{ij}^{\mathrm{plastic}}$ is the plastic strain, and $q^T$ is a heat source.

The coupling to the solid mechanics is via the $\mathcal{E}\nabla ·{\mathbf{v}}_s$ term and the $\nu (1-\varphi ){\sigma }_{ij}^{\mathrm{eff}}\frac{\partial }{\partial t}{ϵ}_{ij}^{\mathrm{plastic}}$ term. The changes in rock porosity and permeability also provide coupling. Coupling to the fluid flow and geochemistry is via the equations of state used in Equation (5), as well as coming from the the source term $q^T$.

We assume that the liquids and solid are in thermal equilibrium locally and that there is a single local temperature in all phases. If this does not hold, one is also normally in the high-flow regime where the flow is non-Darcy as well.

The heat flux is a sum of conduction and convection of heat within the fluid:

$${\mathbf{F}}^T=-\lambda \nabla T+\sum _{\beta }{h}_{\beta }{\mathbf{F}}_{\beta }.$$

(6)

Here, $\lambda$ is the tensor-based thermal conductivity of the combined fluid-rock system, which is a function of the thermal conductivities of both the fluid phases and rock mass. The specific enthalpy of phase $\beta$ is denoted by $h_{\beta }$, and ${\mathbf{F}}_{\beta }$ is the advective Darcy flux.

Mechanics. The majority of the solid mechanics used by the FALCON is provided by the MOOSE Tensor Mechanics module, which was developed from the pure mechanics perspective. This section provides only a brief overview, concentrating on the code aspects that differ from conventional (pure) solid mechanics.

The total stress tensor is denoted by ${\sigma }^{\mathrm{tot}}$. An applied mechanical force will create a perturbation to ${\sigma }^{\mathrm{tot}}$. Resolving ${\sigma }^{\mathrm{tot}}$ into directional components yields the forces on nodes in the finite-element mesh.

The effective stress tensor is denoted by ${\sigma }^{\mathrm{eff}}$. It is defined by

$${\sigma }_{ij}^{\mathrm{eff}}={\sigma }_{ij}^{\mathrm{tot}}+{\alpha }_B{\delta }_{ij}{P}_f.$$

(7)

where $P_f$ is a measure of pore pressure. In single-phase, fully-saturated situations, it is traditional to use $P_f=P_{\beta }$. ${\alpha }_B$ is the Biot coefficient. This obeys $0\le {\alpha }_B\le 1$.

The formulation in FALCON assumes that the elastic constitutive law reads

$${\sigma }_{ij}^{\mathrm{eff}}=E_{ijkl}({ϵ}_{kl}^{\mathrm{elastic}}-{\delta }_{kl}{\alpha }_{T}T),$$

(8)

with ${\alpha }_T$ being the thermal expansion coefficient of the drained porous skeleton, and ${ϵ}_{kl}=({\nabla }_k{u}_l+{\nabla }_l{u}_k)/2$ being the total strain tensor as usually considered; it can be split into the plastic and elastic parts, $ϵ={ϵ}^{\mathrm{plastic}}+{ϵ}^{\mathrm{elastic}}$. $E_{ijkl}$ is the elasticity tensor (the “drained” version).

The conservation of momentum is

$${\rho }_{\mathrm{mat}}\frac{\partial v_s^j}{\partial t}={\nabla }_i{\sigma }_{ij}^{\mathrm{tot}}+{\rho }_{\mathrm{mat}}{b}_j={\nabla }_i{\sigma }_{ij}^{\mathrm{eff}}-{\alpha }_B{\nabla }_j{P}_f+{\rho }_{\mathrm{mat}}{b}_j,$$

(9)

where ${\mathbf{v}}_s=\partial \mathbf{u}/\partial t$ represents the velocity of the rock material skeleton, and ${\rho }_{\mathrm{mat}}$ is the mass-density of the material. $b_j$ are the density components of any external force (for example, the gravitational acceleration).

2. Native State Modeling

The conceptual and earth models of the FORGE reservoir and surrounding area were transitioned into a numerical representation so that the spatial distribution of native state pressure, temperature, and stress conditions could be estimated and used to help plan FORGE operations. The numerical implementation included complex boundary conditions and three-dimensional parameter distributions. The calibrated native state model will establish a reference set of reservoir parameters (and their spatial distribution) that can be used by the geothermal modeling community.

As discussed in the following subsections, the native state model is based on relevant site data and uses very complex boundary and initial conditions to represent the earth model as realistically as possible. The initial reservoir parameters and boundary conditions were modified as needed during calibration of the native state model. The native state model will be updated at regular intervals, corresponding to advances in site characterization and data availability, with annual revisions expected.

2.1. Model Location and Dimensions

The Phase 2 FORGE numerical model domain was sized to accommodate the geothermal reservoir intersected by the site pilot well, Well 58-32, and envisioned future injection and production wells along with their predicted stimulation volumes created during FORGE Phase 3. A model domain of 2.5 km × 2.5 km × 2.75 km was located nominally between 400 m and 3200 m below the land surface (see Figure 3). The mesh was aligned with the principal stress direction (N25E) estimated from borehole breakout and drilling induced fracturing analysis in Well 58-32 [11]. A mesh spacing of 50 m was uniformly used, resulting in a total of 137,500 grid cells.

The lithology was divided into the two broadly defined units from the conceptual model, consisting of granitic basement rocks (granitoid) and the overlying basin fill sedimentary deposits (Figure 3 and Figure 4). The depth to the top of the model domain was chosen so that the entire top of the model was located within the alluvium materials. This was chosen for several reasons:

• To avoid lateral groundwater flow in the near surface sediments originating from the east side of the Opal Mound Structure (the southeast side of the model domain). Little data area available regarding the near surface flow system, but given the near surface temperature distributions, significant lateral flow is likely. This area is of little interest to the present study.
• To avoid the unsaturated portions of the near surface sediments. As we are simulating the system in a fully-coupled thermal-hydrologic-mechanical numerical framework, including the unsaturated zone has practical, and significant, implications for the computational burden and applicability of the equations of state at negative (capillary) pressures. None of these issues are insurmountable, but at the present time, the effort required to overcome them cannot be justified for an area of the site that is not of interest to the present study.
• To facilitate establishment of the stress boundary condition on the top model surface and aid in the calibration of the vertical stress in the model. The use of the Leapfrog Geothermal earth modeling package [28] (see below) allowed for summation of the saturated and unsaturated sediment column above the model domain and applying this as a overburden load on the top of the model domain. This enabled the evaluation of the grain density of the overlying sediments required for model calibration.

The model domain was constructed in geologic modeling software package LeapFrog Geothermal [28]. A commercial earth modeling package was chosen so that property distribution estimates from the FORGE characterization and historical studies could be easily extrapolated onto the numerical grid. The resultant numerical domain and mesh used the same reference universal transverse mercator (UTM) coordinate system which allowed for importing of numerical results back into the earth model for display, comparison, and archiving.

2.2. Reference Discrete Fracture Network

The FORGE reference DFN model was constructed using FracMan software [22]. The DFN incorporates data collected from surface fracture surveys and geophysical well logs to create planar fractures that can act as a single hydrologic and mechanical system. The reference DFN consists of two parts, (1) a deterministic set of fractures where fracture locations and orientations are known to intersect Well 58-32, and (2) a stochastic set of fractures away from well control. The stochastic fracture-set orientations and intensity are based on fracture data from Well 58-32, while fracture sizes were based on nearby trace length data collected in the Mineral Mountains. Multiple realizations can be generated to show a range of possible reservoir natural fracture set populations. Some highlights of the DFN parameterization are discussed in the following section (more details can be found in [29]).

Fracture orientations are based on Formation Micro Scanner (FMI) log interpretation of Well 58-32 [11]. Measured orientations have been weighted using the Terzaghi correction factor [30] using a maximum value of seven. This weighting factor is used to account for the bias introduced by sampling inclined or vertical fractures from a vertical well. Figure 5 shows contour plots of the fracture pole orientations on upper hemisphere stereonets both with and without the Terzaghi weighting. This weighting only affects the apparent concentrations of the fracture poles on contour plots and does not change the locations of the poles which represent the measured fracture orientations. The fractures in the DFN were generated by randomly selecting values from the Terzaghi weighted population and so mirror the measured values quite well. Three sets have been identified for use by other researchers with mean orientations and intensities listed in

Table 1. Fracture set orientations and intensity from Well 58-32 FMI data. Intensity data are based on the Terzaghi weighted distribution. P${}_{32}$ is defined as the total fracture area per unit volume.

	Units	EW Vertical	NS Inclined Dipping West	NE Steeply Dipping SE
Set Intensity	P${}_{32}$ (m${}^{-1}$)	0.78	1.41	0.31
	Percent	31	56	12
Mean Set Orientation	Strike (deg)	96	185	215
	Dip (deg)	80 S	48 W	64 SE

.

Fracture intensity in the FORGE reservoir DFN is also based on the FMI log interpretation of Well 58-32. The lineal fracture intensity, P${}_{10}$, is defined as the number of fractures per unit of length [31,32]. On a cumulative fracture intensity (CFI) plot, the slope of the line shows the inverse of the P${}_{10}$ value, so higher slopes correspond to lower fracture intensities. The CFI plot for 58-32 (Figure 6) shows that there are two distinct regions of fracture intensity: (1) a shallower region extending from the top of the granitoid to a measured depth in the well of approximately 1300 m having higher lineal fracture intensity, and (2) a deeper region extending to the bottom of the well having a lower lineal fracture intensity. This corresponds to the transition from the monzodiorite to the monzonite lithology where the bulk porosity also drops correspondingly. As the FORGE site is primarily investigating the potential for exploitation at deeper, hotter zones, the choice was made to use a single fracture intensity value corresponding to the deeper zone where the P${}_{10}$ is 1.18 m${}^{-1}$.

The P${}_{10}$ intensity measure will vary as a function of the relative angle between the fracture set orientations and the trajectory of the well where the measurement is made. Another fracture intensity measure, the volumetric fracture intensity, P${}_{32}$, is defined as the fracture area per unit of volume. This intensity measure can be derived from the P${}_{10}$ once the fracture orientations of the population are determined and is independent of the original method of collecting the intensity data. Because P${}_{32}$ can be reported independently from the well and fracture set orientations, it is better suited to represent both the relative and total fracture set intensities. Table 1 provides the P${}_{32}$ values of the three fracture sets.

Fracture size was estimated using trace-length data from the nearby outcrops in the Mineral Mountains [34] that are comprised of the same geologic unit that is present in the FORGE reservoir. The trace-length data fit log-normal distributions with an average mean and standard deviation of 57.0 m and 50.4 m, respectively. Measured values fitting a log-normal distribution often represent data sets that are actually present in a power law distribution. Power law distributions that are truncated at both the low and high ends of the range appear as log-normal. Therefore, the trace data were also fit to a power law distribution, as shown in Figure 7. DFNs were created for the FORGE work using both the log-normal distribution and a power law distribution with parameter D equal to 2.6 (negative trace length slope + 1). Depending on the use of the DFN, minimum and maximum size cutoffs were also used during fracture generation. For the reservoir scale model, a minimum fracture radius size of 10 m was used while for well-scale DFNs, a minimum size of 1 m was used. The maximum size of fracture radius was 150 m. Fracture shapes were assumed to be roughly circular and are represented as six-sided polygons.

2.3. Rock and Fluid Properties

Rock and reservoir fluid properties used for the simulations were based on a combination of site characterization results and values from the literature. Because the focus of the research and the majority of the characterization data are from the granitoid reservoir, the majority of the modeling efforts are also focused on the granitoid. As discussed in the following sections, stochastic property distributions were used where justified; otherwise, single parameter values were used.

2.3.1. Hydrologic Properties

Mean bulk porosity of the granitoid reservoir was 1–2% at reservoir depths based on the Well 58-32 neutron porosity log, while core sample porosity measurements were 0.5% [11,33,35,36]. Bulk porosity is composed of both matrix porosity and fracture porosity with the fracture porosity component, ${\varphi }_F$, estimated from upscaling the DFN:

$${\varphi }_F=\frac{\sum A_{F}e}{V_C}$$

(10)

where $A_F$, the fracture area in a grid cell, and e, the fracture aperture, are multiplied together for each fracture in a grid cell and summed, while $V_C$ is the grid cell volume. Apertures are assumed to be linearly related to the square root of the fracture radius, R:

$$e=a\sqrt{R}$$

(11)

The linear coefficient, a, was found through a calibration process so that the mean upscaled fracture porosity was approximately 0.5%. Additional porosity may come from the rock matrix.

The average rock in situ permeability of the granitoid is estimated to be 4.7 × 10${}^{-17}$ m${}^2$ from well testing performed in Phase 2B [17]. In a similar workflow as was utilized to estimate fracture apertures, a relationship between fracture permeability, $k_F$, and aperture is assumed:

$$k_F=b{e}^{1.5}$$

(12)

The linear coefficient, b, is determined by requiring that the upscaled fracture permeability match the measured granitoid permeability. Once upscaled to continuum values, the average directional fracture permeabilities in cell coordinate directions for the granitoid were 6.5 × 10${}^{-17}$ m${}^2$, 6.5 × 10${}^{-17}$ m${}^2$, and 7.0 × 10${}^{-17}$ m${}^2$, respectively. A histogram of the upscaled fracture vertical permeability is shown in Figure 8. Table 2 summarizes the granitoid permeability and porosity.

Permeability and porosity for the sedimentary materials were estimated from aquifer tests conducted at the FORGE site [37], analysis of cuttings collected during the drilling of Well 58-32 [11,33,36], and geophysical well logs collected in Well 58-32 [11,33,36]. As the sedimentary materials were not the focus of this modeling study, single values were used to represent the permeability and porosity, as summarized in Table 3.

2.3.2. Thermal Properties

Thermal properties of the granitoid reservoir and overlying sediments were studied in detail using rock core and cuttings obtained during the drilling of Well 58-32 [11,33,36,38]. Measurements of specific heat capacity and thermal conductivity were made at nominally 33 m (100 ft) intervals along the length of Well 58-32. As we only have data from one well, spatial distributions of these parameters within each unit were not attempted nor justified at the present time; therefore, single values for specific heat capacity and thermal conductivity were used for the granitoid and sedimentary materials. Table 2 and Table 3 summarize the values used.

For long-term operational modeling of the FORGE reservoir, temperature-dependent thermal expansion coefficients will be critical and will require site specific measurements. For the current steady-state modeling efforts, temperature invariant uniform thermal expansion coefficients obtained from the literature [39,40] were used for the granitoid and sedimentary units, as summarized in Table 2 and Table 3.

2.3.3. Mechanical Properties

Mechanical properties of the granitoid reservoir rocks were determined from laboratory analysis of core plugs from Well 58-32, geophysical logs, and values reported in the literature [11,41]. Young’s modulus and Poisson’s ratio were determined from laboratory testing on the two core sections and also measured from well logs. Horizontal and vertical plugs were taken from four different zones in the two cores and tested. Different hydraulic confining pressures were applied to these samples to simulate different stress regimes (near the wellbore where stresses can be elevated because of stress concentrations and away from the wellbore where the stresses are consistent with the measured stresses). The confining pressures ranged from zero (unconfined compression) to 51.7 MPa (7500 psi) [11]. This covers the full range of effective stresses that would be experienced in this reservoir.

Compressional and shear wave travel times from the dipole sonic imager (DSI) and bulk density from the triple combo logging suite (gamma ray, neutron, and density porosity and resistivity) were also used to calculate dynamic elastic properties. Mechanical properties inferred from the logging operations were corrected using the laboratory measurements [11]. The Biot coefficient of the granitoid was taken from the literature [41]. Granitoid mechanical properties are summarized in Table 2.

The mechanical properties Young’s Modulus, Poisson’s Ratio, and Biot coefficient of the sedimentary materials were taken from the literature [42,43,44] and are summarized in Table 3.

2.3.4. Fluid Properties

FALCON uses the MOOSE Fluid Properties module to estimate the fluid density, viscosity, and thermal conductivity. In the native state simulations, a pure water formulation was used. Detailed geochemical modeling and laboratory analysis will be used as inputs for future FORGE reservoir modeling efforts.

The water implementation in fluid properties is the International Association for the Properties of Water and Steam (IAPWS) Industrial Formulation 1997 for the Thermodynamic Properties of Water and Steam [45]. This formulation calculates properties of water and steam using pressure and temperature as inputs. The IAPWS-IF97 formulation is split into five different regions in the phase diagram. All five regions are implemented in the fluid properties module. To avoid iteration in region 3 of the IAPWS-IF97 formulation, the backwards equations from [46] are implemented.

Viscosity is calculated using the IAPWS 2008 formulation [47]. Note that the critical enhancement has not been implemented. Thermal conductivity is calculated using the IAPWS 1985 formulation [48]. Although there is a newer formulation available [49], it is significantly more complicated, so it has not been implemented yet. Dissolution of a dilute gas into water is calculated using Henry’s law [50]. The fluid properties implemented in FALCON are valid for the following temperature and pressure ranges:

• 273.15 K $\le T\le$ 1073.15 K, for $P\le$ 100 MPa;
• 1073.15 K $\le T\le$ 2273.15 K, for $P\le$ 50 MPa.

2.4. Boundary Conditions

The distributions of pressure, temperature, and stress, as determined by site characterization activities [11], have varying degrees of spatial variability in the native state model domain. Translating these distributions to the boundary conditions used in the modeling activities will be discussed in detail in the following sections.

Table 2. Properties for the granitoid reservoir used in the native state simulation. Values based on field and laboratory measurements and model calibration.

Parameter	Units	Min	Max	Source
Permeability${}_{ii}$	m${}^2$	6.9 × ${10}^{-18}$	1.2 × ${10}^{-16}$	Upscaled DFN [29,51] Core-Reservoir testing [11]
Permeability${}_{jj}$	m${}^2$	4.5 × ${10}^{-18}$	1.5 × ${10}^{-16}$	Upscaled DFN [29,51] Core-Reservoir testing [11]
Permeability${}_{kk}$	m${}^2$	6.2 × ${10}^{-18}$	1.1 × ${10}^{-16}$	Upscaled DFN [29,51] Core-Reservoir testing [11]
Porosity	–	1.0 × ${10}^{-7}$	1.2 × ${10}^{-2}$	Upscaled DFN [29,51] Core-Reservoir testing [11]
Specific Heat Capacity	J kg${}^{-1}$ K${}^{-1}$	7.90 × ${10}^2$		Cuttings analysis [38] Literature [52] Model calibration
Grain Thermal Conductivity	W m${}^{-1}$ K${}^{-1}$	3.05		Cuttings analysis [38] Model calibration
Thermal Expansion Coefficient	K${}^{-1}$	6.00 × ${10}^{-6}$		Literature [39]
Rock Grain Density	kg m${}^{-3}$	2.75 × ${10}^3$		Core-cuttings analysis [11] Model calibration
Young’s Modulus	Pa	6.2 × ${10}^{10}$		Core testing [11]
Poisson’s Ratio	–	0.30		Core testing [11]
Biot Coefficient	–	0.60		Literature [41]

Table 2. Properties for the granitoid reservoir used in the native state simulation. Values based on field and laboratory measurements and model calibration.

Parameter	Units	Min	Max	Source
Permeability${}_{ii}$	m${}^2$	6.9 × ${10}^{-18}$	1.2 × ${10}^{-16}$	Upscaled DFN [29,51] Core-Reservoir testing [11]
Permeability${}_{jj}$	m${}^2$	4.5 × ${10}^{-18}$	1.5 × ${10}^{-16}$	Upscaled DFN [29,51] Core-Reservoir testing [11]
Permeability${}_{kk}$	m${}^2$	6.2 × ${10}^{-18}$	1.1 × ${10}^{-16}$	Upscaled DFN [29,51] Core-Reservoir testing [11]
Porosity	–	1.0 × ${10}^{-7}$	1.2 × ${10}^{-2}$	Upscaled DFN [29,51] Core-Reservoir testing [11]
Specific Heat Capacity	J kg${}^{-1}$ K${}^{-1}$	7.90 × ${10}^2$		Cuttings analysis [38] Literature [52] Model calibration
Grain Thermal Conductivity	W m${}^{-1}$ K${}^{-1}$	3.05		Cuttings analysis [38] Model calibration
Thermal Expansion Coefficient	K${}^{-1}$	6.00 × ${10}^{-6}$		Literature [39]
Rock Grain Density	kg m${}^{-3}$	2.75 × ${10}^3$		Core-cuttings analysis [11] Model calibration
Young’s Modulus	Pa	6.2 × ${10}^{10}$		Core testing [11]
Poisson’s Ratio	–	0.30		Core testing [11]
Biot Coefficient	–	0.60		Literature [41]

Table 3. Properties for the sedimentary overburden used in the native state simulation. Values based on field and laboratory measurements and model calibration.

Parameter	Units	Value	Source
Permeability	m${}^2$	1.7 × ${10}^{-14}$	Aquifer testing [11]
Porosity	–	1.2 × ${10}^{-1}$	Aquifer testing [11] Model calibration
Specific Heat Capacity	J kg${}^{-1}$ K${}^{-1}$	8.30 × ${10}^2$	Literature [52]
Grain Thermal Conductivity	W m${}^{-1}$ K${}^{-1}$	2.0	Cuttings analysis [38] Model calibration
Thermal Expansion Coefficient	K${}^{-1}$	2.00 × ${10}^{-6}$	Literature [40]
Rock Grain Density	kg m${}^{-3}$	2.50 × ${10}^{10}$	Cuttings analysis [11] Model calibration
Young’s Modulus	Pa	3.0 × ${10}^{10}$	Literature [42]
Poisson’s Ratio	–	0.30	Literature [43]
Biot Coefficient	–	0.60	Literature [44]

Table 3. Properties for the sedimentary overburden used in the native state simulation. Values based on field and laboratory measurements and model calibration.

Parameter	Units	Value	Source
Permeability	m${}^2$	1.7 × ${10}^{-14}$	Aquifer testing [11]
Porosity	–	1.2 × ${10}^{-1}$	Aquifer testing [11] Model calibration
Specific Heat Capacity	J kg${}^{-1}$ K${}^{-1}$	8.30 × ${10}^2$	Literature [52]
Grain Thermal Conductivity	W m${}^{-1}$ K${}^{-1}$	2.0	Cuttings analysis [38] Model calibration
Thermal Expansion Coefficient	K${}^{-1}$	2.00 × ${10}^{-6}$	Literature [40]
Rock Grain Density	kg m${}^{-3}$	2.50 × ${10}^{10}$	Cuttings analysis [11] Model calibration
Young’s Modulus	Pa	3.0 × ${10}^{10}$	Literature [42]
Poisson’s Ratio	–	0.30	Literature [43]
Biot Coefficient	–	0.60	Literature [44]

2.4.1. Temperature

Temperatures in the model region were predicted to be between 60 ${}^{\circ }$C and 250 ${}^{\circ }$C based on measurements in Well 58-32 and numerous temperature gradient wells in the vicinity of the FORGE site [38], which resulted in a complex 3D thermal structure in the vicinity of the FORGE site. The complex temperature distribution is due to the interaction of thermal fluids moving through the upper sediments around a portion of the Opal Mound Fault and conduction from what is taken to be an irregularly shaped thermal regime at depth.

The 3D interpolation of the temperature data, developed in LeapFrog, was mapped onto the numerical model grid as assigned to all sides of the model domain as a Dirichlet boundary condition, as shown in Figure 9. The values for the top surface of the model domain ranged from approximately 55 ${}^{\circ }$C to over 90 ${}^{\circ }$C. Allis et al. [38] originally set a maximum temperature of 250 ${}^{\circ }$C in their predictions as they had no way to justify using higher values. As was done for the top temperature boundary, the 3D interpolation of the temperature data was mapped onto the numerical model grid and assigned to the bottom of the model domain. As part of the model calibration exercise, the temperatures Allis et al. used for portions of the base of the earth model domain had to be raised to allow the modeled temperature to match the November 2018 logging data. The bottom temperature values ranged from approximately 220 ${}^{\circ }$C to nearly 270 ${}^{\circ }$C (see Figure 9). This temperature is largely controlled by conduction from the heat source originating/hosting the hydrothermal system to the east.

2.4.2. Pressure

The top surface of the model domain (see Figure 4) was assigned a Dirichlet condition for pressure. The pressure values were estimated by calculating the height of the water column between the top of the model domain and the water table [11]. The water table in the vicinity of the FORGE site slopes in a generally westward direction, resulting in the pressure gradient across the top of the model domain. The water column height was uniformly adjusted as part of the calibration process, until the modeled pressure matched the values obtained from the pressure measurements in Well 58-32 collected in November 2018. Figure 10 shows the pressure applied to the top of the model domain.

All other boundaries of the model domain were assumed to be impermeable. While this assumption may not be perfectly valid for the upper sedimentary sections, the model domain was chosen in order to omit as much of the sedimentary section as possible to avoid having to consider lateral flow originating from the outflow around the terminus of the Opal Mound Fault. The extremely low permeability of the granitoid justifies a no-flow condition (see Table 2).

2.4.3. Stress

The boundary condition for total vertical stress is perhaps one of the most important for FORGE, as it will have a direct influence on predicted stress gradients at the site. Therefore, a significant amount of effort was used to develop this condition. Values for all stress components were estimated using results from stress testing in Well 58-32 from Phase 2B [51], pore-pressure information (from the pressure boundary condition discussed above), density of the sedimentary materials overlying the granite, and the land-surface topography at the site. Note that any mention of stress refers to the total stress.

A Dirichlet condition for stress (as a total body force) was applied to the top of the model domain. Included in the vertical stress boundary condition is topographic expression of land surface features (such as the Mag Lee Wash that runs through the site) and the saturated thickness of groundwater, resulting in a range of 8.0 to 11.2 MPa being applied (see Figure 11). The bottom surface of the modeled domain was set to zero displacement in the vertical direction and a roller condition in the horizontal directions.

A gradient of 0.014 MPa/m (0.62 psi/ft) was applied to the east side of the model domain (S${}_h$ direction), while the left/west was fixed at zero displacement. Values ranged from approximately 8 MPa to over 45 MPa. A S${}_H$ gradient of 0.0174 MPa/m (0.77 psi/ft) was applied to the back side of the model domain, while the front was fixed at zero displacement. Values ranged from approximately 11 MPa to nearly 55 MPa. Figure 11 shows the stress values used on the boundaries.

These boundary conditions were chosen so that the model could honor the available data and so that the simulation results could be used to provide stress distributions on the model edges that can be used for transient simulations of injection/production at the site.

2.5. Initial Conditions

Initial pressure, temperature, and stress conditions used for the native state model were based on data in the earth model. These data were assigned to the numerical model in a similar manner as was done to assign the boundary conditions. Pressure values were estimated starting from the top boundary condition, and then interpolated downward as a function of depth. Temperature information was directly mapped from the earth model to the numerical model domain. Stress is a derived quantity in FALCON’s numerical formulation, based on calculations of the displacement of the rock matrix. It is difficult to assign a priori; therefore, a value of zero displacement was assigned for the entire model domain as an initial condition. The model was allowed a number of additional iterations to come to an initial solution.

Reservoir hydraulic, thermal, and mechanical properties used in the native state model were initially taken from the site characterization data. In many cases, a range of possible values was available; in these cases, a mean was used as an initial estimate, with the values being adjusted within the measured range during model calibration. For the alluvium, uniform reservoir properties were used. For the granitoid, heterogeneous property distributions were used where appropriate and data were available. Table 2 and Table 3 provide a summary the property values. These values can be considered the “reference” values for the native state of FORGE at the end of Phase 2.

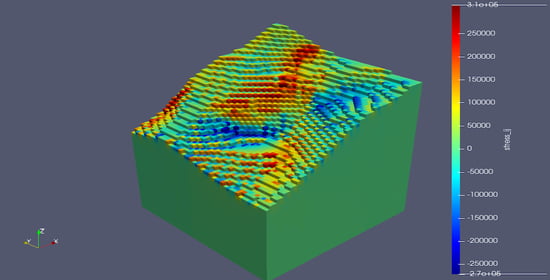
3. Results

The model calibration process consisted of first initializing the model with initial and boundary condition values for pressure, temperature, and stress obtained from the earth model and comparing the simulated values with those obtained from measurements and logging in Well 58-32. In order to calibrate the pressure, the height of the water table was uniformly adjusted up and down until the modeled pressure distribution matched the logged values from Well 58-32.

In order to calibrate the modeled temperature field, several adjustments had to be made. These involved manually varying the thermal conductivity of both the granitoid and sedimentary units. In order to obtain a match with field measurements, the temperatures at the bottom of the earth model had to be reinterpreted (raised from 250 ${}^{\circ }$C to 270 ${}^{\circ }$C) for portions of the inferred heat source underlying the site. This change required the entire thermal structure at the site to be re-estimated followed by regenerating the model initial and boundary conditions. This process was repeated iteratively until an acceptable match was obtained between the simulated temperature field and the measured values in Well 58-32.

Figure 12 presents the modeled pressure, temperature, and stress along the trajectory of Well 58-32 with the data from pressure-temperature logging collected in November 2018. As seen in Figure 12, the simulated pressure and temperature match the well log data quite well. The pressure distribution is linear along the length of well and shows little differentiation between the alluvium and granitoid materials. The modeled temperature distribution for Well 58-32 also matches the field data well and shows a break in slope at the sediment-granitoid contact. Input and mesh files for the native state simulations can be found in the Geothermal Data Repository [53].

The stress-gradient data from Phase 2 were collected in the toe of Well 58-32. In Figure 12, the gradient estimate is plotted over the entire length of Well 58-32, along with the modeled native state stress. The vertical stress was calibrated by adjusting the density and porosity of the sediments and granitoid (within the range of measured values) until the modeled vertical stress approximated the field estimates. The simulated minimum and maximum horizontal stresses were slightly overestimated but were within the range of measured values.

Figure 13 and Figure 14 show this simulated native state pressure and stress on the edges of the model domain. Temperature results not plotted as Dirichlet conditions were assigned on all sides of the domain. The pressure results for the bottom of the model domain show significant variation, largely due to the significant differences in the thermal regime (see Figure 9). As shown in Figure 9, the temperature assigned to the bottom of the model domain ranged from approximately 220 ${}^{\circ }$C to 270 ${}^{\circ }$C, resulting in fluid density differences of over 70 kg/m${}^3$.

Topographic effects resulted in significant variation in vertical stress, as shown in Figure 14. The general westward slope of the land surface (i.e., thicker overburden on the eastern side of the model domain) resulted in an approximate 3 MPa difference in the stress applied to the top boundary. Superimposed on the westward slope of the ground surface was the topographic expression of the Mag Lee Wash. The effects of both the slope and wash are reflected in the predicted vertical stress on the bottom surface of the model.

As part of the planning for future injection and production wells at the FORGE site, a number of potential trajectories were evaluated as part of the Phase 2 activities. A full discussion of the well evaluation procedure is beyond the scope of this paper. Here, we focus on providing information on the final selected well trajectory. Figure 15 shows the final selected well trajectory (Well 16A-78(32)) along with an outline of the FORGE site. The well will be located near the center of the FORGE site, with a planned trajectory that travels along an azimuth of N15E, plunging 65 degrees from the vertical. The predicted pressure, temperature, and stress along the planned path of Well 16A-78(32) are shown in Figure 16.

4. Summary and Conclusions

Geologic characterization activities combined with historical information culminated in a conceptual model of the site which is dominated by thermal conduction in a large granitoid body with a top surface that dips generally to the west. The granitoid reservoir is overlain by younger sedimentary materials that host a non-potable groundwater resource. A reference earth model was constructed based on the geologic conceptual model that will be used to assess all future changes in geologic understanding at the site.

A detailed native state thermal-hydraulic-mechanical model of the region where stimulation and operations are expected to occur was created based upon the reference earth model. The modeled boundary conditions were mapped directly from geologic, geographic, and hydrogeologic conditions measured at the site and were modified along with select reservoir properties to come to a calibrated steady-state solution. A reference set of reservoir flow, heat transport, DFN, and mechanical properties was developed from the calibration exercise and used by the team for follow-on modeling to ensure comparability of results. Considerable care and attention were placed into developing the framework of the native state numerical model. The geologic structure developed in the earth model was mapped onto a uniform 50 m grid, on a domain that is generally centered around Well 58-32 and the region where Phase 3 activities are envisioned to take place. The numerical representation of the earth model comprised two general geologic units: sedimentary/alluvial materials that overlie a granitoid basement.

Hydrologic and mechanical properties of the sedimentary materials were considered to be spatially uniform and based on data collected as part of FORGE characterization or from the literature. This unit, however, is not part of the reservoir, so the native state modeling efforts did not focus on this unit. The complete top of the model domain was set to be in the sediments for the convenience of setting it to top-boundary conditions (body forces). The granitoid materials that make up the planned EGS reservoir were assigned a heterogeneous and anisotropic permeability field based upon the reference DFN developed for the site. The porosity was also based on the upscaled DFN, while other reservoir properties (such as density and thermal conductivity) were assigned uniform values.

For the stress model, we incorporated detailed surface topography and relief of granite contact, as these can cause perturbations in the stress field at depth. The native- state model shows small perturbations in Shmin that generally follow the granite-alluvium contact and, in some areas, several hundred meters into the granitoid materials. Calibration of the native state model consisted of adjusting the grain density and porosity of the sediments and the density of the granitoid in order to match the field estimate measured in Well 58-32. The thermal conductivity of both the sediments and granitoid was slightly modified from initial estimates, as was the maximum temperature at the base of the earth model. Reservoir permeability was taken from upscaling the reference DFN and went unchanged in the native state model. Only the top boundary pressure was modified to ensure it matched the measured values at Well 58-32.