1. Introduction
Battery- and fuel cell-powered vehicles have attracted increasing attention during the last decade [
1,
2,
3,
4,
5,
6,
7,
8]. They offer an alternative to internal combustion engines which are primarily based on the consumption of fossil fuels. From the technological point of view, battery-powered vehicles are advantageous for short driving ranges up to 160 km [
9]. This number may be taken as a rough guideline, as in real world applications, other terms, such as the availability of a charging infrastructure [
10] and prices for competing transport solutions [
8,
11], are also important. All of these criteria strongly affect the social acceptance of electric vehicles, as shown by Burkert et al. [
12] in their analysis of Germany from 2011 to 2020.
In order to increase the driving range, a battery system can be combined with a fuel cell. The term ‘fuel cell vehicle’ is commonly used for hybrid systems in which the the main power is delivered by the fuel cell system, and the battery is merely used to cover highly dynamic load changes [
13]. In the case of a range extender, the fuel cell system mainly operates as a more or less constant charging unit for the battery, which acts as the primary power unit. The main challenge for such range extenders is to provide extra power without adding significantly to the complexity of the fuel cell system. Furthermore, this should come at low additional costs in terms of payload and sale price.
Recently, a number of commercial cars have been released as battery-powered models with a polymer electrolyte fuel cell system used for range extension. Among these, the Renault Kangoo was presented in 2015 and uses a 5 kW fuel cell system [
14,
15]. Another example is the Fiat 500 passenger car equipped with a 30 kW fuel cell system [
16,
17,
18]. In order to reduce weight, the system operates on dry air and hydrogen and employs the anodic recirculation of product water. As a special application for utility vehicles, the company Proton Motor introduced a 7 kW range extender [
16,
19] with the main goal of reducing the required battery size. Despite these highly successful demonstrations, there remain some issues to be resolved. One of the major goals is the further reduction of costs for the range extender, as a competitive selling price is always a key target for emerging technologies. This issue is addressed by the CoBIP project, in which the mass production of metallic bipolar plates in a role-to-role process is developed [
20]. The goal of the project is the production of a modular 24 kW system for a light-duty commercial vehicle [
21], as displayed in
Figure 1. The fuel cell system will be mounted on the roof of a battery-powered car. The figure shows a system consisting of four stacks, a high-pressure hydrogen tank, and heat exchangers. The rooftop position favors a flat and light-weight design. The fuel cells will be operated without additional humidifier in order to reduce the system’s weight and complexity.
The overall production process combines the techniques of calendering, laser welding, laser cutting, coating, and stack assembly. Each production step adds some requirements to the final flow field plates, as summarized by Porstmann et al. [
22]. In general, there are two different design options for bipolar plates, which depend on the plate material. There are compact plates (mostly graphitic) where structures may be milled or thin metallic plates which can be stamped [
22,
23]. For graphitic plates, it is possible to design the flow fields for anode, cathode and coolant more or less independently. In the case of plates made from thin metal sheets, it is possible to integrate cooling into the plate design of the anode and cathode. Here, each plate defines the gas flow field on one side and half of the coolant flow field on the back side [
23,
24,
25]. The final cell plate consists of an anode plate and a cathode plate welded together and is, therefore, called a double-plate concept. This adds additional complexity to the overall design process, as the combination of two plates yields three different flow fields.
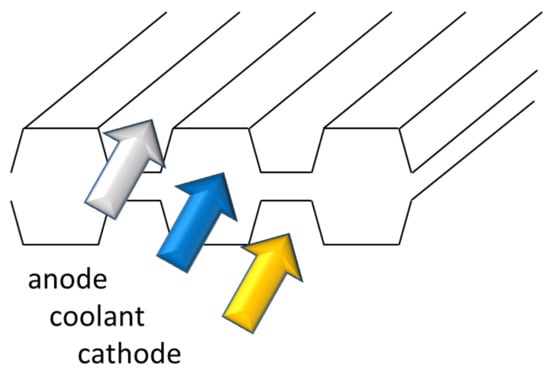
Figure 2 shows a cross section of such an arrangement and aptly demonstrates that the final arrangement is highly compact and features a high utilization of the available space.
In the literature, a vast number of different flow field designs exist that may be used in polymer electrolyte fuel cells. In general, a few basic flow field types, such as parallel, pin type, serpentine, interdigitated, and wave, may be distinguished, which are discussed, amongst other topics in the reviews of Li and Sabir [
24], Kahraman and Orhan [
26], Sauermoser et al. [
27], and Wilberforce et al. [
28]. These basic types can be modified according to the specific needs of the target application. A recent review by Çelik et al. lists 33 modified flow field designs [
29] for performance enhancement. Manso et al. analyzed the influence of the geometric parameters on the performance of PEFCs in their review [
30]. A major problem for such a comparison is that the operating conditions for each original study can significantly differ [
30]. Therefore, it is important to separately consider each cell design within the context of its application. As a general statement, it can be concluded that serpentine and interdigitated designs usually achieve a more uniform reactant distribution [
30]. The counter flow configuration of anode and cathode show better membrane hydration, thus increasing the overall cell performance [
30]. A ratio of channel/rib
is advantageous for operation at lower current densities, and a ratio of channel/rib
shows better performance at higher current densities [
30,
31,
32]. In order to improve the performance of particular flow field types, several optimization strategies have been reported. Liu and Wang reported a coupled modeling and experimental testing procedure for PEFCs with a very wide channel within a single serpentine configuration [
33]. Under the given operating conditions, a channel/rib ratio close to unity was obtained, namely a channel width of 1.0 mm and a rib width of 0.8 mm. Ghanbarian et al. investigated parallel serpentine flow fields with different number of channels [
34]. They also concluded that a channel/rib ratio of unity is the best option. For small channels with a width < 1 mm, Cooper et al. [
35] found that not only the ratio of channel/rib is important, but also the hydraulic diameter. By applying a design of experiments approach, they found an optimum for hydraulic diameters in the range of 0.40 to 0.45 mm. Limjeerajarus and Charoen-amornkitt [
36] compared in their numerical study a small test cell with serpentine and straight channel arrangements. They demonstrated the importance of a proper flow distribution over the active area, especially if the channels of a straight parallel flow field are supplied by a single channel as a distributor. It is a common feature of all flow fields with multiple channels that the flow must be distributed as evenly as possible from an inlet pipe to the separate channels. This topic is addressed in the works of Ramos-Alvarado et al. [
37] and Lim et al. [
38] regarding straight channel flow fields. They show that it is possible to distribute the flow from a smaller inlet area by introducing suitable distributor structures within the active cell area. The performance can be further optimized by changing the shape of the channel cross section, as described by Wang et al. [
39] for triangles, semicircles, and trapezoidal shapes [
39,
40]. It is also possible to use drilled in holes in a through plane array [
41] or straight channels with bulges [
42] or indentations [
43]. Finally, the flow field can also be composed of a fine mesh, as shown for the Toyota fuel cell system [
1,
44].
The discussion thus far has mainly been derived from single cell experiments, in which active cooling is not required. The assembly of several cells into a stack raises the need to remove excess heat. There are several techniques that can be chosen for the cooling of a PEFC system. The reviews of Zhang and Kandlikar [
45], Bargal et al. [
46], and Li et al. [
47] provide a comprehensive overview of this topic. The simplest method is so called ‘passive cooling’, which makes use of the high heat conductivity of the flow field plate material. This method is primarily used for devices with smaller power outputs [
45]. An ‘active cooling’ system, in contrast, refers to one in which a fluid is actively pumped through a separate cooling flow field. The fluid can be air, but, for higher power densities, a liquid coolant is typically used because the heat transfer is more effective for a liquid with the same pumping power [
45]. An even higher cooling effect can be achieved, if the heat of evaporation of a liquid is used instead of heat transfer to a fluid [
48]. A deeper discussion, together with an optimization strategy of the channel shape for evaporative cooling, can be found in the work of Soupremanien et al. [
49]. A well known application of this principle can also be found in heat pipe devices, as demonstrated by Clement and Wang [
50] and Supra et al. [
51,
52] in their studies for fuel cell applications. Each of these cooling technologies increases demands on the construction of the fuel cell stack. In this paper, cooling with a liquid is considered, as this technique offers the highest compactness for the integrated design shown in
Figure 2. The application of a liquid coolant, in turn, requires the existence of a coolant flow field. An obvious solution to this is to use a similar approach as in the flow fields discussed above for the distribution of hydrogen and air [
45,
46]. Again, many different variants of these flow fields are discussed in the literature. The main purpose of the coolant flow field is to generate a desired temperature profile across the active area. In most cases, homogeneous temperature distribution is preferred, which can be experimentally verified through the use of infrared thermography [
53]. A special approach is to utilize metal meshes or foams for the coolant flow field. Afshari et al. compared these with straight channel and serpentine arrangements [
54]. The metal foam exhibits improved heat transfer facilitated by the larger inner surface at the price of an increased flow resistance. The approaches that have been discussed thus far require a separate coolant flow field; in many cases, this means a separate cooling cell, such as an internal heat exchanger. Matsunaga et al. (Honda) [
55] presented a different solution that is especially suitable for the application of thin metal plates (see
Figure 2). The flow channels exhibit a wave-like pattern that allows the coolant to pass through on the back side.
In most of the cited literature, the design of the flow field is performed with the goal of improving fuel cell performance. This is a challenging task, as such, as there are many physical processes to be considered that are all directly or indirectly coupled. The work of Alaswad et al. [
56] provides a good overview of the influence of operating parameters on fuel cell performance. Performance can, in turn, only be measured if a working fuel cell already exists. The focus of this work is to derive a design strategy for the initial step of flow plate design. Many parameters arise from the manufacturing process that must be taken into account, and which have a high impact or imply severe constraints on the overall design. The novelty of this work is the development of such a design process that allows the creation of two bipolar plates and, respectively, three flow fields, in one design step. It is demonstrated how the large number of influencing parameters can be incorporated by an effective modeling approach. The impact of uncertainty on the modeling results is investigated, and the consequences for the final results are discussed. A toolbox is provided in the
supplementary material which assists in the automated design screening steps.