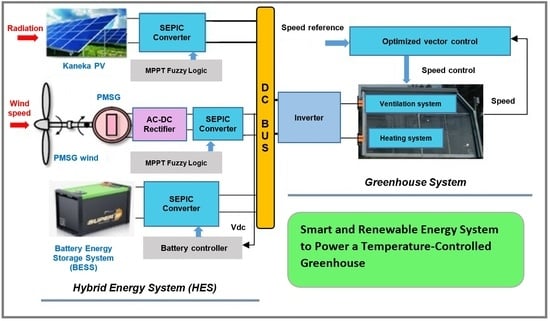
Smart and Renewable Energy System to Power a Temperature-Controlled Greenhouse †
Abstract
:1. Introduction
2. Modeling of the Energy System
2.1. Model of the PV Generator
2.2. Model of the Wind Turbine
2.3. Model of the Battery Energy Storage System
2.4. SEPIC Buck Boost Converter
2.5. Fuzzy Logic for the MPPT
2.6. Greenhouse Model
2.7. Real Experimental Greenhouse in the Faculty of Sciences in Tunis
3. Control Strategy of the Global System
3.1. Control of the MSPS and BESS
- Power generated by the MSPS exceeds the power required by the load: the excess is stored in the battery bank and, when the battery bank will be full, the further energy will be dissipated in a load shedding system, which is a resistor in this study.
- Generated power is equal to the power required by the load: the produced power is entirely injected into the DC bus to the load.
- Power delivered by the MSPS is insufficient and the battery is charged: the missing power will be supplied by the battery storage system and the battery bank will be controlled to be activated when the SOC state is in the operating range.
3.2. Control Strategy of the Ventilation/Heating System
4. Simulation Results and Discussion
4.1. Electrical Behavior of the PV Generator
4.2. Electrical Behavior of the Wind Turbine
4.3. Simulation of the MSPS under Control Strategy
4.4. Simulation Results of the Global System
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Riahi, J.; Vergura, S.; Mezghani, D.; Mami, A. A combined PV-wind energy system for an energy saving greenhouse. In Proceedings of the IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020; pp. 1–6. [Google Scholar]
- Diab, F.; Lan, H.; Zhang, L.; Ali, S. An environmentally friendly factory in Egypt based on hybrid photovoltaic/wind/diesel/battery system. J. Clean. Prod. 2016, 112, 3884–3894. [Google Scholar] [CrossRef] [Green Version]
- Huang, P.-H.; Kuo, J.-K.; Wu, Z.-D. Applying small wind turbines and a photovoltaic system to facilitate electrolysis hydrogen production. Int. J. Hydrogen Energy 2016, 41, 8514–8524. [Google Scholar] [CrossRef]
- JFulzele, B.; Daigavane, M.B. Simulation and optimization of hybrid PV-wind renewable energy system. In Proceedings of the 3rd International Conference on Electrical, Electronics, Engineering Trends, Communication, Optimization and Sciences (EEECOS 2016), Tadepalligudem, India, 1–2 June 2016. [Google Scholar]
- Allani, M.Y.; Jomaa, M.; Mezghani, D.; Mami, A. Modelling and simulation of the hybrid system PV-wind with MATLAB/SIMULINK. In Proceedings of the 9th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 20–22 March 2018. [Google Scholar]
- Gautam, A.R.; Mahela, O.P.; Singh, S.; Mahia, R.N. A double input SMV controlled dc/dc buckboost converter for solar PV/wind energy sources. In Proceedings of the International Conference on Recent Advances and Innovations in Engineering (ICRAIE-2014), Jaipur, India, 9–11 May 2014; pp. 1–6. [Google Scholar]
- Qi, W.; Liu, J.; Chen, X.; Christofides, P.D. Supervisory Predictive Control of Standalone Wind/Solar Energy Generation Systems. IEEE Trans. Control Syst. Technol. 2011, 19, 199–207. [Google Scholar] [CrossRef]
- Vergura, S.; Pavan, A.M. On the photovoltaic explicit empirical model: Operations along the current-voltage curve. In Proceedings of the IEEE-ICCEP 2015 International Conference on Clean Electrical Power, Taormina, Italy, 16–18 June 2015. [Google Scholar]
- Vergura, S. Correct Settings of a Joint Unmanned Aerial Vehicle and Thermocamera System for the Detection of Faulty Photovoltaic Modules. IEEE J. Photovolt. 2021, 11, 124–130. [Google Scholar] [CrossRef]
- Vergura, S.; Marino, F. Quantitative and Computer Aided Thermography-based Diagnostics for PV Devices: Part I—Framework. IEEE J. Photovolt. 2017, 7, 822–827. [Google Scholar] [CrossRef]
- Vergura, S.; Colaprico, M.; de Ruvo, M.F.; Marino, F. A Quantitative and Computer Aided Thermography-based Diagnostics for PV Devices: Part II—Platform and Results. IEEE J. Photovolt. 2017, 7, 237–243. [Google Scholar] [CrossRef]
- Sineglasov, V.M.; Dmitrenko, B.I.; Kulbaka, A.V. Using PV/wind hybrid systems in the autonomous power of unmanned aerial vehicle control centre. In Proceedings of the IEEE 2nd International Conference Actual Problems of Unmanned Air Vehicles Developments (APUAVD), Kyiv, Ukraine, 15–17 October 2013. [Google Scholar]
- Maher, A.; Kamel, E.; Enrico, F.; Atif, I.; Abdelkader, M. An intelligent system for the climate control and energy savings in agricultural greenhouses. Energy Effic. 2016, 9, 1241–1255. [Google Scholar] [CrossRef]
- Echaieb, K.; Azaza, M.; Mami, A. A new control strategy of indoor air temperature in a photovoltaic greenhouse. Int. J. Soft Comput. Softw. Eng. 2013, 3, 848–852. [Google Scholar]
- Stoyanov, L.; Bachev, I.; Zarkov, Z.; Lazarov, V.; Notton, G. Multivariate Analysis of a Wind–PV-Based Water Pumping Hybrid System for Irrigation Purposes. Energies 2021, 14, 3231. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations. Water for Sustainable Food and Agriculture: A Report Produced for the G20 Presidency of Germany. Available online: http://www.fao.org/3/i7959e/i7959e.pdf?fbclid=IwAR1eV3HuHfHdxH6ca11yhMBTD6U78LnwqUxZlKrTWaxfUgOQF4rpuFwJtWo (accessed on 13 August 2021).
- Salisu, S.; Mustafa, M.W.; Olatomiwa, L.; Mohammed, O.O. Assessment of technical and economic feasibility for a hybrid PV-wind-diesel-battery energy system in a remote community of north central Nigeria. Alex. Eng. J. 2019, 58, 1103–1118. [Google Scholar] [CrossRef]
- Krishan, O.; Suhag, S. Techno-economic analysis of a hybrid renewable energy system for an energy poor rural community. J. Energy Storage 2019, 23, 305–319. [Google Scholar] [CrossRef]
- Wesly, J.; Brasil, A.C.P.; Frate, C.A.; Badibanga, R.K. Techno-economic analysis of a PV-wind-battery for a remote community in Haiti. Case Stud. Chem. Environ. Eng. 2020, 2, 100044. [Google Scholar] [CrossRef]
- Gorjian, S.; Calise, F.; Kant, K.; Ahamed, S.; Copertaro, B.; Najafi, G.; Zhang, X.; Aghaei, M.; Shamshiri, R.R. A review on opportunities for implementation of solar energy technologies in agricultural greenhouses. J. Clean. Prod. 2021, 285, 124807. [Google Scholar] [CrossRef]
- ATraoré, K.; Cardenas, A.; Doumbia, M.L.; Agbossou, K. Comparative Study of Three Power Management Strategies of a Wind PV Hybrid Stand-alone System for Agricultural Applications. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 1711–1716. [Google Scholar]
- Islam, A.; Merabet, A.; Beguenane, R.; Ibrahim, H. Power Management Strategy for Solar-Wind-Diesel Stand-alone Hybrid Energy System. Int. J. Electr. Comput. Energ. Electron. Commun. Eng. 2014, 8, 849–853. [Google Scholar]
- Al-Ghussain, L.; Ahmed, H.; Haneef, F. Optimization of hybrid PV-wind system: Case study Al-Tafilah cement factory, Jordan, Sustain. Energy Technol. Assess. 2018, 30, 24–36. [Google Scholar] [CrossRef]
- Singh, P.; Ravindra, N. Temperature dependence of solar cell performance—An analysis. Sol. Energy Mater. Sol. Cells 2012, 101, 36–45. [Google Scholar] [CrossRef]
- Luque, A.; Hegedus, S. Handbook of Photovoltaic Science and Engineering; John Wiley and Sons: Chichester, UK, 2003. [Google Scholar]
- Markvart, T.; Castaner, L. Practical Handbook of Photovoltaics. Fundamentals and Applications; Elsevier: Oxford, UK, 2006. [Google Scholar]
- Vergura, S. Scalable Model of PV Cell in Variable Environment Condition based on the Manufacturer Datasheet for Circuit Simulation. In Proceedings of the IEEE-EEEIC 2015, Roma, Italy, 10–13 June 2015. [Google Scholar]
- Vergura, S. A Complete and Simplified Datasheet-Based Model of PV Cells in Variable Environmental Conditions for Circuit Simulation. Energies 2016, 9, 326. [Google Scholar] [CrossRef]
- Vergura, S. Hypothesis Tests-Based Analysis for Anomaly Detection in Photovoltaic Systems in the Absence of Environmental Parameters. Energies 2018, 11, 485. [Google Scholar] [CrossRef] [Green Version]
- Joonmin, L.; Young-Seok, K. Sensorless fuzzy-logic-based maximum power point tracking control for a small-scale wind power generation system with a switched mode rectifier. IET Renew. Power Gener. 2016, 10, 194–202. [Google Scholar]
- Charfi, S.; Atieh, A.; Chaabene, M. Modeling and cost analysis for different PV/battery/diesel operating options driving a load in Tunisia, Jordan and KSA. Sustain. Cities Soc. 2016, 25, 49–56. [Google Scholar] [CrossRef]
- Allani, M.Y.; Tadeo, F.; Mezghani, D.; Mami, A. Modelling and Control of a Grid–connected Hybrid Photovoltaic/wind/battery System Coupled to an AC Load. IJSCNS 2019, 19, 5. [Google Scholar]
- Borowy, B.S.; Salameh, Z.M. Methodology for optimally sizing the combination of a battery bank and PV array in a wind/PV hybrid system. IEEE Trans. Energy Convers. 1996, 11, 367–375. [Google Scholar] [CrossRef]
- Daud, A.-K.; Ismail, M.S. Design of isolated hybrid systems minimizing costs and pollutant emissions. Renew. Energy 2012, 44, 215–224. [Google Scholar] [CrossRef]
- Mezghani, D.; Othmani, H.; Mami, A. Bond graph modeling and robust control of a photovoltaic generator that powered an induction motor pump via SEPIC converter. Electr. Energy Syst. 2019, 29, e2746. [Google Scholar] [CrossRef]
- Mezghani, D.; Mami, A.; Dauphin-Tanguy, G. Bond graph modelling and control enhancement of an off-grid hybrid pumping system by frequency optimization. Int. J. Numer. Model. 2020, 33, e2717. [Google Scholar] [CrossRef]
- Riahi, J.; Vergura, S.; Mezghani, D.; Mami, A. Intelligent Control of the Microclimate of an Agricultural Grennhouse Powered by a Supporting PV System. Appl. Sci. 2020, 10, 1350. [Google Scholar] [CrossRef] [Green Version]
- Ben Ali, R.; Bouadila, S.; Mami, A. Experimental validation of the dynamic thermal behavior of two types of agricultural greenhouses in the Mediterranean context. Renew. Energy 2019, 147, 118–129. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, W. H2 optimal speed regulator for vector-controlled induction motor drives. In Proceedings of the 27th Chinese Control and Decision Conference (2015 CCDC), Qingdao, China, 23–25 May 2015. [Google Scholar]
- Miki, I.; Nagai, N.; Nishiyama, S.; Yamada, T. Vector control of induction motor with fuzzy PI controller. In Proceedings of the 1991 IEEE Industry Applications Society Annual Meeting, Dearborn, MI, USA, 28 September–4 October 1991. [Google Scholar]
- Zhu, X.; Shen, A. Speed Estimation of Sensorless Vector Control System Based on Single Neuron PI Controller. In Proceedings of the 2006 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006. [Google Scholar]
- Othmani, H.; Mezghani, D.; Mami, A. Fuzzy Gain-Scheduling Proportional–Integral control for Improving the speed behavior of a three-phases induction motor. Int. J. Power Electron. Drive Syst. (IJPEDS) 2016, 7, 1161. [Google Scholar] [CrossRef] [Green Version]
- Chaouali, H.; Othmani, H.; Mezghani, D.; Jouini, H.; Mami, A. Fuzzy logic control scheme for a 3 phased asynchronous machine fed by Kaneka GSA-60 PV panels. In Proceedings of the 7th IEEE International Conference Renewable Energy Congress, Hammamet, Tunisia, 22–24 March 2016. [Google Scholar]


























| Component | Value |
|---|---|
| Cin, Cout | 440 uF |
| Cp | 10 uF |
| L1, L2 | 47 uH |
| Rules | Ev | Ep | D |
|---|---|---|---|
| 1 | P | P | P |
| 2 | N | P | P |
| 3 | Z | P | P |
| 4 | Z | Z | Z |
| 5 | N | Z | P |
| 6 | P | Z | N |
| 7 | P | N | N |
| 8 | N | N | P |
| 9 | Z | N | P |
| Rule N° | E | ΔET | Cem |
|---|---|---|---|
| 1 | P | P | P |
| 2 | P | Z | P |
| 3 | P | N | P |
| 4 | Z | P | P |
| 5 | Z | Z | Z |
| 6 | Z | N | N |
| 7 | N | P | N |
| 8 | N | Z | N |
| 9 | N | N | N |
| Rule N° | E | Kp |
|---|---|---|
| 1 | N | N |
| 2 | Z | Z |
| 3 | P | P |
| Rule N° | E | dE | Ki |
|---|---|---|---|
| 1 | P | P | P |
| 2 | P | Z | P |
| 3 | P | N | P |
| 4 | Z | P | P |
| 5 | Z | Z | Z |
| 6 | Z | N | N |
| 7 | N | P | N |
| 8 | N | Z | N |
| 9 | N | N | N |
| Technical Specifications | Nominal Values |
|---|---|
| Nominal power, Pn | 60 Wp |
| Minimum Power | 57 W |
| Voltage at Pmax, Vmpp | 67 V |
| Current at Pmax, Impp | 0.9 A |
| Open circuit voltage, Voc | 92 V |
| Short-circuit current, Isc | 1.19 A |
| Actuator | Electrical Parameters | Nominal Power |
|---|---|---|
| Ventilation System | 3 phase–50 Hz | 705 W |
| Heating system | 230 V, 50/60 Hz | 1000 W |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riahi, J.; Vergura, S.; Mezghani, D.; Mami, A. Smart and Renewable Energy System to Power a Temperature-Controlled Greenhouse. Energies 2021, 14, 5499. https://doi.org/10.3390/en14175499
Riahi J, Vergura S, Mezghani D, Mami A. Smart and Renewable Energy System to Power a Temperature-Controlled Greenhouse. Energies. 2021; 14(17):5499. https://doi.org/10.3390/en14175499
Chicago/Turabian StyleRiahi, Jamel, Silvano Vergura, Dhafer Mezghani, and Abdelkader Mami. 2021. "Smart and Renewable Energy System to Power a Temperature-Controlled Greenhouse" Energies 14, no. 17: 5499. https://doi.org/10.3390/en14175499
APA StyleRiahi, J., Vergura, S., Mezghani, D., & Mami, A. (2021). Smart and Renewable Energy System to Power a Temperature-Controlled Greenhouse. Energies, 14(17), 5499. https://doi.org/10.3390/en14175499