1. Introduction
Rear-side reflectors are a commonly used way to increase the performance of evacuated tube collectors (ETC) by reflecting the otherwise non-usable incident solar energy between the evacuated tubes back to the absorber. Furthermore, the use of reflectors can lead to a reduction in the number of evacuated tubes while maintaining the same collector power output, which will result in a lower collector cost overall, since the reflector material is significantly cheaper than the evacuated tubes.
The disadvantage of using reflectors is the increased investment cost, a higher maintenance requirement as well as a higher wind and snow load [
1]. In recent years, reflectors have been mainly designed to improve their performance, e.g., by improving the geometry or the material properties, but not to decrease their cost. With the reduction of the reflector cost, the investment cost for the solar thermal collector and thus the levelized cost of heat (LCoH) [
2] can be reduced. This can be achieved through several methods, like the use of cheaper reflective material, a more manufacturable geometry or by the use of alternative elements that were not actually intended for use as reflectors.
This paper presents ray-tracing simulations using both a low-cost, diffusely reflecting reflector, which is commonly used as a roof covering, as well as a high-quality, directly reflecting reflector. The diffuse reflector is eight times cheaper than the directly reflecting reflector. Due to its trapezoidal geometry, the diffuse reflector does not need additional mounting support to keep the reflector in shape (as is the case with, e.g., CPC reflectors). Furthermore, if the roof for the solar thermal installation is already equipped with the same or a similar roof covering, there is no need for an additional reflector.
The results were validated experimentally using thermal performance measurements on selected collectors in accordance with ISO EN 9806:2017 [
3]. The influence of the rear reflectors on collector yield (annual collector output) as well as on annual yield in a typical solar thermal domestic hot water system (SDHW) was investigated by means of simulations based on the measured collector parameters.
The use of reflectors in commercially available ETCs represents today’s state of the art. In 1976, NASA started a project to increase the performance of an ETC working with air made by Owens-Illinois [
4]. They used two different types of diffuse reflectors (DR). The first one was made of a white-painted aluminum, while the second one was made of white vinyl sidings. They investigated the effect of the tube spacing both theoretically and experimentally, resulting in a maximum daily collector efficiency at a tube spacing of 1.5–2 times of the tube diameter [
5]. In 1980, O’Gallagher et al. [
6] investigated different types of rear-side reflectors for ETCs with cylindrical absorbers, but largely focused on concentrating reflectors. Window et al. released a study in 1981 in which both diffuse and specular reflectors (SR) were used and evaluated [
7,
8]. For the DR, they used a flat, white- painted reflector and for the SR, they used a compound parabolic collector (CPC) made of aluminum. The maximum collector efficiency occurred at a tube spacing of around 1.5 for both reflector types. Under these geometrical conditions, the SR led to a higher efficiency (in comparison with the DR) of around 6.5%. Geometric variations were also carried out for the diffuse reflector in respect to the distance between the tubes and the reflector. For a given tube spacing of 2 times the tube diameter, the maximum collector efficiency was found at 1.3 times the tube diameter, with a small influence on increasing reflector distances. Chow et al. [
9,
10] found similar results, but with a closer look at the optical properties of the components used. In more recent times, Milani and Abbas [
11] gave a good overview of the scientific work conducted in recent decades regarding rear-side reflectors. They investigated flat diffuse-reflecting rear-side reflectors and provided recommendations about the best tube spacing (3.0) and reflector distance (1.5) for a given tube diameter. Depending on different locations in Australia, the use of a reflector, as well as the adjustment of tube distances, led to an increase in solar energy gain of a domestic hot water system of up to 28% compared to a collector without a reflector. Kalogirou [
12] predicted, without giving any more detailed information, an increase in the absorbed energy of each tube of more than 25% for normal irradiance by using rear-side reflectors. Furthermore, the resultant increase in the solar energy yield for one day with the given configuration is about 10%. Dubey and Arora [
13] used a diffusely reflecting flat plate on the rear-side of an ETC for a solar still system. The enhancement in daily condensate yield was found to be approx. 15% compared with the system without a reflector.
The literature review has shown, that in most cases, specular reflectors in different variations or flat diffuse reflectors were investigated, but for the reduction of the collector cost, the use of a cost-efficient reflector is necessary. The diffuse reflector we propose consists of a sheet of metal commonly used as a roof covering. It is therefore manufactured for the mass market and is characterized by its low production cost. Therefore, the influence of this reflector on the thermal performance of an evacuated tube collector has to be investigated in order to evaluate potential cost savings for the solar thermal market.
In
Section 2, we simulated the collector in a ray-tracing program and investigated the performance as well as its angular dependence for different reflector geometries and materials. Based on this investigation, we were able to perform thermal system simulations with TRNSYS in
Section 3 and to evaluate the influence of the different reflectors when used in a typical domestic hot water system.
3. TRNSYS Simulation: Annual Collector Output and System Simulation
The simulations for the annual collector output and the system yield were both carried out with the TRNSYS simulation tool for the location of Würzburg (Germany). The non-standard TRNSYS types as well as the weather data used in the simulations are shown in
Table A2 in
Appendix A. The simulated domestic hot water system (
Figure 10) is characterized by the boundary conditions listed in
Table A3 in
Appendix A.
The collector simulated is a heat-pipe collector with a temperature limitation of 125 °C. All collector characteristic values used for the simulation were derived from a real test system and can be found in
Table 4. The used collector type 832 was intentionally developed by Perers and Bales [
23] and was further developed by Schiebler et al. [
24] to represent the heat pipe dry-out effect and thus the temperature limitation of the collector. The IAM factors used correspond to the results of the previous investigations (
Section 2), which showed that the IAM factors of the different reflectors can be simulated with maximum deviations of approx. 4.5%.
The IAM-factors can be simulated with greater accuracy at small irradiation angles than at large irradiation angles (cf.
Figure 6 in
Section 2). In order to consider this effect, the influence of the deviating IAM factors on the simulation results is examined. For this purpose, a further data set with scaled IAM factors was created in addition to the previous simulated IAM-factors. This represents the deviations shown in
Table 3 between measurement and simulation data for the whole angular range.
Figure 11 shows this procedure exemplarily for the specular reflector.
The value assumed for the deviation is based on the average occurring deviations between measured data and simulation results (cf.
Table 3), and thus, it also considers the investigation conducted by Weißmüller et al. [
21]. This comprehensive comparison between European test institutes already shows a maximum deviation of 4.5% between the participating institutes in the determination of the IAM factors.
3.1. Annual Collector Output
The annual collector energy output allows a first, simplified estimate of the efficiency of the collectors. This is primarily used by testing institutes and certification bodies in order to enable the comparison of different types of collectors under different weather conditions. The calculation assumes a constant load and a constant operating temperature over the course of the year. The corresponding simulations were carried out for the location Würzburg (Germany) with an operating temperature of 50 °C and an aperture area of about 6 m
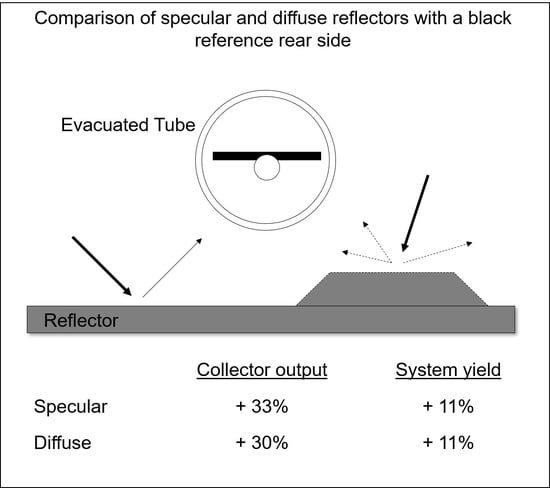
2. Through the use of the reflectors, a significant increase in the annual solar yield could be achieved (
Figure 12). Compared to the black reference rear-side, the specular reflector leads to an increase of approximately 33%, while the diffuse reflector leads to an increase of approximately 30%. Under consideration of the different boundary conditions used, this result corresponds well to the investigations of diffuse reflectors by Milani and Abbas [
11] (+28%) and Kalogirou [
12] (+25%).
Simulations with scaled IAM factors (
Table 5) show changes in yield of approximately ±2.5% for the specular reflector and ±1.4% for the diffuse reflector result. Thus, the influence of the simulated IAM factor deviations on the annual collector output is small.
Regarding the geometry variations (cf.
Section 2.3), the tube distance was scaled between 1.3 and 3 times the outer tube diameter (which corresponds to the original configuration of 60 tubes (100%) and a reduced amount of 30 tubes (50%)) for both reflector configurations. Due to the increased reflectance, when the tube distance is increased, the loss in solar annual yield does not increase proportionally to the decrease in surface area (
Figure 13). For a 10% reduction in the aperture area, the loss in yield is approximately 8% for the specular and 9% for the diffuse reflector. The yield loss with a 50% reduction in area is 44% for the specular reflector and 46.5% for the diffuse reflector.
The simulation shows that the use of a rear-side reflector increases the annual collector energy output significantly, which particularly affects large-scale solar systems (e.g., solar district heating). Furthermore, the reflectors can, in comparison with the original configuration (3585 kWh), be used to maintain the same annual collector output while reducing the number of tubes. A collector with a number of tubes reduced by 30% will lead to an annual collector output of approximately 3600 kWh (specular) or 3400 kWh (diffuse).
3.2. System Simulation of a Solar DHW System
Especially in solar small-scale systems, the solar yield is reduced by so-called “system-related effects”. These include, for example, stagnation, the state of thermal storage, control behavior or other unpredictable events. In order to evaluate the different reflectors in a solar small-scale system with the limitation of system-related effects, the annual system yield of a standard domestic hot water system for the location of Würzburg and with the aforementioned collector characteristics was simulated with TRNSYS. All the necessary simulation parameters can be taken from
Table A3 in
Appendix A.
Figure 14 shows the comparison between the system yields using the different reflector geometries. First of all, it should be pointed out that the difference in system yield between the specular and the diffuse reflectors is extremely small, at approximately 2% (6 kWh), although the specular reflector has a significantly better reflectivity and also achieves a higher annual collector output.
Due to the system-related effects, the advantage of the specular reflector over the diffuse reflector in the system is limited. For the diffuse reflector configuration, the overall operation time of the solar pump is about 3% (around 50 h) longer in comparison with the specular reflector configuration, but both systems will reach the same solar yield at the end of the day. Therefore, it can be concluded that, on the one hand, the specular configuration reaches stagnation faster than the diffuse configuration. On the other hand, the specular configuration will start its solar operation later, since the storage temperature is higher.
Table 6 shows the results of both the original system simulation and the simulation with scaled IAM factors. The influence of the simulated IAM factor deviations on the system simulation are at ±0.7% (specular) and ±0.4% (diffuse), even smaller than for the annual collector output.
The aperture area (number of tubes) of the collectors was also reduced for the DHW system.
Figure 15 shows the annual solar system yield, analogous to the collector yield, for the DHW system with a decreasing aperture area. The difference between the specular and diffuse reflectors in annual solar yield increases steadily with a reduction in the aperture area. In contrast to annual collector yield, the percentage yield reduction is not proportional to the reduction in area. For a reduction in aperture area of 10%, specular and diffuse reflectors only show a reduced yield of about 3%. The reduced yield with a 50% reduction in area is 25% (specular) and 27.5% (diffuse).
Similar to the annual collector output, the system yield of the investigated DHW system is also increased by the use of the proposed reflectors. To maintain the same system yield of the reference rear-side configuration (2715 kWh), the tubes can be reduced by 20%, which will lead to a system yield of approximately 2825 kWh (specular) or 2802 kWh (diffuse); this can be reduced further by 30%, which will lead to a system yield of approximately 2686 kWh (specular) or 2647 kWh (diffuse).
4. Discussion
Reducing the cost of solar thermal systems is an essential factor in promoting their use and thus reducing CO2 emissions. One approach to reduce these costs is to either increase the performance of evacuated tube collectors by using rear-side reflectors or to reduce the number of tubes used while maintaining the same collector performance.
In this paper, the performance of an evacuated tube collector with different rear-side reflectors was analyzed by means of ray-tracing simulations as well as annual collector output and system simulations. Specifically, a diffusely reflecting, low-cost, galvanized trapezoidal sheet metal which is usually used as a roof covering and a high-quality, planar mirror sheet made of aluminum (speculary reflecting) were compared.
By means of ray-tracing analysis, the η0 values of the configurations were determined and plausibility could be checked with the help of real collector measurement data. Furthermore, the IAM factors of the different configurations were determined up to a solar incidence angle of 60°. The IAM factors can be well simulated in the range of 0–30° with a deviation of 1.5% for the diffuse and 1.6% for the specular reflector and with an increasing deviation in the range of 30–60° (2.7% diffuse/7.3% specular). Based on these results, geometrical adjustments were made to the tube spacing (number of tubes) and the distance between the tubes and the reflector.
The annual yield simulations performed show, in comparison to a black reference rear-side, an additional yield of 30% (collector yield) and 11% (system yield) for the use of the diffuse reflector and 33% (collector yield) and 11% (system yield) for the use of the specular reflector. The differences between the diffuse and the specular reflectors are therefore unexpectedly small. Thus, the low-cost diffuse reflector offers an attractive alternative to the high-quality specular reflectors currently established on the market.
The geometrical variation of the aperture area (number of tubes) shows an almost proportional correlation between the collector yield and the area reduction. Minor deviations of this proportionality result from better IAM factors due to the increased tube spacing. In the simulation of a specific DHW system, the influence of the area reduction with the selected boundary conditions is significantly lower. A reduction in the aperture area of 50% leads to a 25% (specular) and 27.5% (diffuse) lower solar yield.
The results show that the efficiency of the evacuated tube collectors considered can be significantly increased by using rear-side reflectors. The reflectors can be used to achieve higher solar yields as well as to reduce the collector area or the number of tubes while maintaining the same solar yields. Regarding the annual collector output, the number of tubes can be reduced by 30% while maintaining the same yield as the black reference rear-side. In terms of the DHW system yield, the number of tubes can be reduced by 20–30%.
Based on the performance evaluation carried out within the scope of this work, an economic assessment and optimization can be made assuming the cost for vacuum tubes and reflector materials. In particular, the diffuse reflector can be regarded as extremely attractive for use in future collector configurations.