Cascade Control of the Ground Station Module of an Airborne Wind Energy System

Abstract

An airborne wind energy system (AWES) can harvest stronger wind streams at higher altitudes which are not accessible to conventional wind turbines. The operation of AWES requires a controller for the tethered aircraft/kite module (KM), as well as a controller for the ground station module (GSM). The literature regarding the control of AWES mostly focuses on the trajectory tracking of the KM. However, an advanced control of the GSM is also key to the successful operation of an AWES. In this paper we propose a cascaded control strategy for the GSM of an AWES during the traction or power generation phase. The GSM comprises a winch and a three-phase induction machine (IM), which acts as a generator. In the outer control-loop, an integral sliding mode control (SMC) algorithm is designed to keep the winch velocity at the prescribed level. A detailed stability analysis is also presented for the existence of the SMC for the perturbed winch system. The rotor flux-based field oriented control (RFOC) of the IM constitutes the inner control-loop. Due to the sophisticated RFOC, the decoupled and instantaneous control of torque and rotor flux is made possible using decentralized proportional integral (PI) controllers. The unknown states required to design RFOC are estimated using a discrete time Kalman filter (DKF), which is based on the quasi-linear model of the IM. The designed GSM controller is integrated with an already developed KM, and the AWES is simulated using MATLAB and Simulink. The simulation study shows that the GSM control system exhibits appropriate performance even in the presence of the wind gusts, which account for the external disturbance.

1. Introduction

The kinetic energy of wind tends to increase with altitude and is much higher at altitudes between 0.5–12 km above the ground than in the proximity of the surface, cf. [1]. In order to exploit these abundant wind resources, the wind turbine manufacturers are constantly working to increase the size of wind turbine systems. However, such scaling-up of the systems requires more material for tower structure and foundations, which results in an increased cost. Apart from financial constraints there are also some physical constraints that limit the size of a wind turbine. There is a consensus that such higher-altitude winds, even 500 m, cannot be reached by any towered turbine without a radical change of concept. In this scenario, airborne wind energy systems (AWES) aim at playing a vital role to convert wind at higher altitudes to electricity. The seminal work of Loyd, cf. [2] paved the way for the development of AWESs. He computed the maximum energy extracted from AWESs with tethered wings. The main concept of AWES can be illustrated by the idea of replacing the tips of blades of a wind turbine by a tethered airfoil, e.g., a soft kite or rigid wing, which is connected to a ground station, cf. [3,4].

AWES can be classified into two major classes: Ground-gen AWES (GG-AWES) and fly-gen AWES (FG-AWES), depending on where the electricity is generated, cf. [4,5]. In GG-AWES, the tether provides the mechanical energy to the generator housed in the ground station. Whereas, in Fly-Gen systems the electricity is generated on board the flying device. In this type of AWES, the tether is used to conduct electricity from the aircraft to the ground station. GG-AWES are further classified as fixed and moveable GG-AWES, and both types are extensively used by industrial and academic researchers. In this research we focus on fixed GG-AWES that are operated in pumping cycle. A pumping kite generator operates in two phases: Traction (generation phase) and retraction (recovery phase). In traction mode the electricity is generated and in retraction phase, a small amount of energy is consumed. The tether which is connected to the drone/kite/aircraft and the ground station is wound on a winch, which is connected to the rotor of an electric machine. In traction mode, the aircraft is driven in a crosswind flight. The lift produced by the aircraft induces tractive force on the tether and consequently mechanical energy is provided to the electrical machine, which acts as a generator. In retraction phase, the machine acts as a motor and rewinds the tether, bringing the aircraft down. The energy produced in the traction phase should be significantly greater than the energy consumed in the retraction mode. The most efficient paths during the crosswind flight are circular or figure-of-eight for maximum power production, cf. [4,6,7]. This is guaranteed by designing a sophisticated control system for an AWES.

1.1. Related Work

Two main objectives of an AWES control system are maximizing the power generation and maintaining a safe and reliable operation, cf. [7,8]. These sometimes conflicting goals are achieved by the automatic control of AWES. However, the time varying and uncertain nature of the wind at the time scale of interest make the feedback control of AWES a formidable task. In normal operating conditions, an AWES control system needs to manage three distinct operational phases: Launch, power generation, and landing. Moreover, the control system needs to ensure smooth inter phase transitions, cf. [7]. The operational phases of an AWES differ significantly in terms of operating conditions and control objectives, therefore, every phase has its own local control strategy to achieve a certain control objective. In order to ensure co-operation between the ground station and on-board kite controllers, a supervisory control is employed which manages the switching between different operational phases. Owing to the contradicting control objectives for different operational phases of an AWES, the overall control of AWES is quite challenging and there is considerable room to improve upon existing literature. In [6], the authors have conducted a pioneering work for the control of AWES in all operational modes, which includes take-off, transition to power generation, pumping energy generation cycles, transition to hovering, and landing.

Most of the literature pertaining to the AWES control deals with the control of crosswind flight and pumping operation. In pumping action control, the preferred reference trajectory for traction phase is a figure-of-eight or circular/elliptical path, whereas, in retraction phase the reference path is a straight line. A common strategy for the control of the kite in crosswind flight is discussed in [9,10,11,12]. In this technique, a continuous Lemniscate parametrization is chosen for the figure-of-eight path. The path can be discretized to obtain a fixed number of waypoints along the path, cf. [13,14]. Other techniques are more abstract, which calculate the desired flight direction either by determining the current active waypoint or reference point on the path, cf. [15]. Apart from the pumping cycle control, a fully autonomous AWES also requires an efficient control of launch and landing phases. An AWES can be launched whenever the environmental conditions are favorable to generate electricity. However, the landing phase is more technical: The aircraft needs to be landed when the conditions are not suitable for electricity generation or there is a fault in the system. The system level launch and land strategies have been explored in [16,17], whereas, specific solutions and phases are discussed in [6,18,19]. In most of the above techniques, it has been assumed that the states required for the synthesis of model-based control are directly available for measurement. However, this assumption is not realistic. In the literature, several approaches have been proposed for an unknown state and parameter estimation pertaining to AWES, and for reducing the effect of sensor noise, cf. [20,21].

One of the major objectives of an AWES control is to maximize the output power. This can be achieved by realizing performance levels as close to the theoretical limits of Loyd’s work in [2] as possible. This needs to be achieved while respecting several operational constraints. In this scenario the role of optimization and hence optimal control is very pertinent to AWES. Therefore, several approaches have been reported in the literature, which include offline optimal control for performance prediction, cf. [22,23,24,25]; model predictive control (MPC): For pumping mode AWES, cf. [26], for real-time simulation studies, cf. [27], and robust MPC, cf. [28]; and adaptive control techniques: Extremum seeking control, cf. [29] and iterative learning control, cf. [30].

As compared to the control of KM, the control of electric machine pertaining to GSM is not discussed by many researchers. The contributions of Hisham et al. [31,32] provide a detailed account on the fault tolerant control of electrical drives for GG-AWES. In order to keep a higher efficiency of the electric machine during the pumping cycle, the concept of dual three phase machines (DTMs) is used. The idea is demonstrated using interior permanent magnet synchronous machine (IPMSM), which is rewinded as a DTM. In [33], the authors design power control strategies for controlling the active and reactive power of an AWE farm.

1.2. Research Gap

Two fundamental components of GG-AWES are the ground station module (GSM) and the kite module (KM). The GSM comprises a winch, an electrical machine, and their respective control systems, whereas, the aircraft/drone and its on-board controllers constitute the KM. As discussed above, the literature regarding the control of AWES mainly focuses on the trajectory control of aircraft in a pumping cycle. An advanced control of the GSM and its integration with the KM controllers have not been fully discussed in the literature. In [6], the authors propose a comprehensive control strategy for all operational phases of AWES. However, the control of the GSM is based on a simplified winch-machine model. An electric machine has a pivotal role in the success of an AWES. In [31], an efficient fault tolerant control of electric drives pertaining to GG-AWES is discussed, however, the focus is not on the coupling of the electric machine with winch and the KM. A cascade control strategy for the electric machine and winch is required to provide a desired winch velocity to the KM.

1.3. Major Contributions

In this manuscript we propose a cascaded control of the GSM during the traction or power-production phase. The GSM, together with the KM, form the two main components of the AWES. The focus of research work is the GSM and the development of its controllers therefore, the KM is considered as a black box which takes the winch velocity as the input and yields tether force as the output. For simulations, we use known models and algorithms for the KM and its controller, namely the the ones in [34,35].

The GSM comprises a winch and a 3-phase induction machine (IM), which can operate either as a motor or as a generator. The cascaded GSM controller provides the desired reel-out winch velocity to KM in traction phase. The GSM control strategy is composed of inner and outer feedback loops. The slower outer-loop represents the winch speed control system, whereas, the faster, inner control-loop is for obtaining the desired torque of the IM. A model-based robust sliding mode control (SMC) algorithm, cf. [36] is used to design the winch speed controller. A detailed stability analysis is also provided for the SMC controller for the perturbed winch system. On the other hand, the control of the IM is based on its 2-phase $d-q$ model, cf. [37,38]. For the high performance control of the IM, the rotor flux oriented control (RFOC), cf. [39] technique is used, which enables a DC machine-like control of the two phase IM model. By virtue of RFOC, the torque and flux control problem is decoupled in such a way that the decentralized control of both torque and flux is possible. Moreover, both torque and flux of the IM can be controlled instantaneously. The decentralized controllers are of the proportional-integral (PI) type. The torque controller tracks the desired trajectory of the torque which is required to obtain a desired winch speed. Whereas, the flux controller tracks an optimum flux trajectory, which minimizes the losses in the IM. It is pertinent to mention here that the unknown states of the IM, which are used in RFOC are estimated using a discrete-time Kalman filter (DKF), which is based on the quasi-linear model of IM, cf. [40]. The conventional linearization based on the Taylor series expansion only gives the approximation of the non-linear system around a fixed operating point, therefore, the linear system is valid in a small operating range. On the other hand, the quasi-linear approach transforms the non-linear system into a state-space form comprising state dependent matrices. Moreover, the exact non-linear dynamics of the system remains intact. Subsequently, the estimation of unknown states is improved. To evaluate the performance of the proposed strategy, the simulations are performed in Matlab/Simulink. The already developed strategy of [34] is used to simulate and analyze the KM. The simulation results show that AWES demonstrates the desired performance, even in the presence of external disturbance in the form of wind gusts.

The remaining article is organized in the following manner. A detailed discussion on the mathematical models of the winch and IM is presented in Section 2. The cascaded control of the GSM is discussed in Section 3. The results are discussed and presented in Section 4 and the article is concluded in Section 5.

2. Modeling of Ground Station Module

As discussed earlier, the GSM is composed of a winch and an IM. The objective of this module is to operate KM at the prescribed velocity, which depends upon the operating phase of an AWES. In this section the control-oriented mathematical models of a winch and IM are discussed.

2.1. Mathematical Model of Winch

The application of the Newton’s second law of rotation on the winch yields (cf. [6]):

$$\begin{array}{cc}\hfill J_w{\dot{\omega }}_w& =|F_T|r_w-b_w{\omega }_w+T_{w_i}+\zeta \left(t\right),\hfill \end{array}$$

(1)

where $J_w$, $b_w$, ${\omega }_w$, and $r_w$ are the inertia, damping coefficient, rotational speed, and radius of winch, respectively; $F_T$ and $T_{w_i}$ represent tether force and IM torque, respectively; and $\zeta \left(t\right)$ is the unknown norm bounded disturbance: $\left|\right|\zeta \left(t\right)\left|\right|\le {\zeta }_0\in {\Re }^{+}$, which accounts for the torque generated by the wind gusts.

$T_{w_i}$ and $F_T$ are exogenous inputs with reference to the winch. The positive sign with $T_{w_i}$ in (1) shows that the winch is providing mechanical power to the IM, which is acting as a generator.

2.2. Mathematical Model of Induction Machine

The dynamic behavior of an IM is complex because the rotor is rotating with respect to the stationary stator. Due to the rotation of the rotor, the coupling coefficients become a function of the rotor position, therefore, the mathematical model of the IM becomes time varying, rendering it difficult for control and estimation applications. For obtaining a control-oriented model of an IM, a reference frame transformation is carried out, which essentially converts a three-phase ($3-\varphi$) machine into its two-phase ($2-\varphi$) equivalent $d-q$ model, where d refers to the direct and q represents the quardature axis. It is pertinent to mention here that the d and q axes are orthogonal to each other. The $2-\varphi$ IM models are categorized as stationary and synchronously rotating reference frame models. In the stationary reference frame (SRF), the coordinate system does not rotate and is fixed in the stator of the machine. Whereas in a synchronously rotating reference frame (SRRF), the coordinate system rotates with synchronous speed (${\omega }_e$), cf. [38]. Throughout this article, the quantities in SRF are represented by superscript s, while the SRRF variables do not have any superscript.

The conversions between $3-\varphi$ and $2-\varphi$ IM models are possible by employing Clarke’s and Park’s transformations, cf. [39]. The first step in RFOC is to convert the $3-\varphi$ IM model into a $2-\varphi$ SRF model by applying Clarke’s transformation as:

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{f}_{qs}^s\\ f_{ds}^s\\ f_{ns}^s\end{array}\right]& ={\displaystyle \frac{2}{3}}\left[\begin{array}{ccc}cos\left(\theta \right)& cos\left(\theta -{120}^{\circ }\right)& cos\left(\theta +{120}^{\circ }\right)\\ sin\left(\theta \right)& sin\left(\theta -{120}^{\circ }\right)& sin\left(\theta +{120}^{\circ }\right)\\ 0.5& 0.5& 0.5\end{array}\right]\left[\begin{array}{c}{f}_{as}\\ f_{bs}\\ f_{cs}\end{array}\right],\hfill \end{array}$$

(2)

where $f_{as}$, $f_{bs}$, and $f_{cs}$ represent an arbitrary quantity (current, flux or voltage) in $3-\varphi$ symmetrical (the phases are exactly 120${}^{\circ }$ apart from each other) $as-bs-cs$ axes, respectively; $f_{ds}^s$ and $f_{qs}^s$ represent $d-q$ axes quantities in SRF, respectively; and $\theta$ is the angle between $f_{as}$ and $f_{qs}^s$. We are assuming that the $3-\varphi$ system is balanced, therefore, the neutral quantity $f_{ns}^s=0$.

Subsequently Park’s transformation is used in the following manner to convert SRF to SRRF:

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{f}_{qs}\\ f_{ds}\end{array}\right]& =\left[\begin{array}{cc}cos\left({\theta }_e\right)& -sin\left({\theta }_e\right)\\ sin\left({\theta }_e\right)& cos\left({\theta }_e\right)\end{array}\right]\left[\begin{array}{c}{f}_{qs}^s\\ f_{ds}^s\end{array}\right],\hfill \end{array}$$

(3)

where ${\theta }_e$ is the angle between $f_{qs}$ and $f_{qs}^s$.

It is pertinent to mention here that both rotation matrices used in (2) and (3) are invertible, hence inverse transformations are also possible and are required during different stages of RFOC.

Both $2-\varphi$ models of an IM, i.e., SRRF and SRF are employed for designing a model-based RFOC. The controller design is carried out using the SRRF model, whereas, the flux estimator is based on the SRF model. The mathematical models of IM in SRRF and SRF are given below.

2.2.1. $d-q$ Model of an Induction Machine in Synchronously Rotating Reference Frame

The mathematical model of the IM in SRRF is adapted from [41,42], and is given as:

$$\begin{array}{cc}\hfill {\displaystyle \frac{d}{dt}}{i}_{qs}& =-k_1{i}_{qs}+k_2{\varphi }_{qr}-k_3{w}_r{\varphi }_{dr}-{\omega }_e{i}_{ds}+k_4{u}_{qs}\hfill \\ \hfill {\displaystyle \frac{d}{dt}}{i}_{ds}& =-k_1{i}_{ds}+k_2{\varphi }_{dr}+k_3{w}_r{\varphi }_{qr}+{\omega }_e{i}_{qs}+k_4{u}_{ds}\hfill \\ \hfill {\displaystyle \frac{d}{dt}}{\varphi }_{qr}& =-k_5{\varphi }_{qr}-N_P\left(w_e-w_r\right){\varphi }_{dr}+k_6{i}_{qs}\hfill \\ \hfill {\displaystyle \frac{d}{dt}}{\varphi }_{dr}& =-k_5{\varphi }_{dr}+N_P\left(w_e-w_r\right){\varphi }_{qr}+k_6{i}_{ds},\hfill \end{array}$$

(4)

where $i_{ds}$ and $i_{qs}$ represent $d-q$ axes currents of stator windings in SRRF, respectively; ${\varphi }_{dr}$ and ${\varphi }_{qr}$ represent the rotor $d-q$ fluxes in SRRF, respectively; $u_{ds}$ and $u_{qs}$ represent $d-q$ axes stator voltages in SRRF, respectively; and ${\omega }_r$ is the electrical speed of the rotor. The constants $k_i$ depend on the construction of the machine and are given as:

$$\begin{array}{cc}\hfill & k_1={\displaystyle \frac{(L_m^2{R}_r+L_r^2{R}_s)}{\sigma L_s{L}_r^2}},k_2={\displaystyle \frac{L_m{R}_r}{\sigma L_s{L}_r^2}},k_3={\displaystyle \frac{n_p{L}_M}{\sigma L_s{L}_r}},\hfill \\ \hfill & k_4={\displaystyle \frac{1}{\sigma L_s}},k_5={\displaystyle \frac{R_r}{L_r}},k_6={\displaystyle \frac{L_m{R}_r}{L_r}},\sigma =1-{\displaystyle \frac{L_m^2}{L_s{L}_r}},\hfill \end{array}$$

where $R_r$ and $R_s$ are resistances of rotor and stator windings, respectively; and $L_r$, $L_s$, and $L_m$ represent the rotor, stator, and magnetizing inductances, respectively.

The electrical speed of the rotor ${\omega }_r$ used in the SRRF model in (4) can be obtained by typical mechanical loading of the motors, and is characterized by:

$$\begin{array}{cc}\hfill {\displaystyle \frac{d}{dt}}{\omega }_r& ={\displaystyle \frac{N_P}{J}}\left(T_e-T_L\right)-{\displaystyle \frac{b}{J}}{\omega }_r,\hfill \end{array}$$

(5)

where J and b are equivalent rotor inertia and damping coefficient, respectively, and $T_e$ and $T_L$ are electromagnetic and load torques, respectively. The expression for $T_e$ in SRRF is given as:

$$\begin{array}{cc}\hfill T_e& ={\displaystyle \frac{3N_P{L}_m}{2L_r}}\left({\varphi }_{dr}{i}_{qs}-{\varphi }_{qr}{i}_{ds}\right),\hfill \end{array}$$

(6)

where $N_P$ denotes the number of pole pairs.

The mechanical (${\omega }_m$) and electrical speeds of the rotor are related through the number of pole pairs as:

$$\begin{array}{cc}\hfill {\omega }_m& ={\displaystyle \frac{{\omega }_e}{N_P}}.\hfill \end{array}$$

(7)

2.2.2. $d-q$ Model of an Induction Machine in Stationary Reference Frame

In SRF, the synchronous speed ${\omega }_e=0$. The differential equations for the currents and fluxes for the squirrel cage induction machine are given as:

$$\begin{array}{cc}\hfill {\displaystyle \frac{d}{dt}}{i}_{qs}^s& =-k_1{i}_{qs}^s+k_2{\varphi }_{qr}^s-k_3{w}_r{\varphi }_{dr}^s+k_4{u}_{qs},\hfill \\ \hfill {\displaystyle \frac{d}{dt}}{i}_{ds}^s& =-k_1{i}_{ds}^s+k_2{\varphi }_{dr}^s+k_3{w}_r{\varphi }_{qr}^s+k_4{u}_{ds},\hfill \\ \hfill {\displaystyle \frac{d}{dt}}{\varphi }_{qr}^s& =-k_5{\varphi }_{qr}^s+N_P{w}_r{\varphi }_{dr}^s+k_6{i}_{qs}^s,\hfill \\ \hfill {\displaystyle \frac{d}{dt}}{\varphi }_{dr}^s& =-k_5{\varphi }_{dr}^s-N_P{w}_r{\varphi }_{qr}^s+k_6{i}_{ds}^s.\hfill \end{array}$$

(8)

2.3. Coupling of Winch and Induction Machine

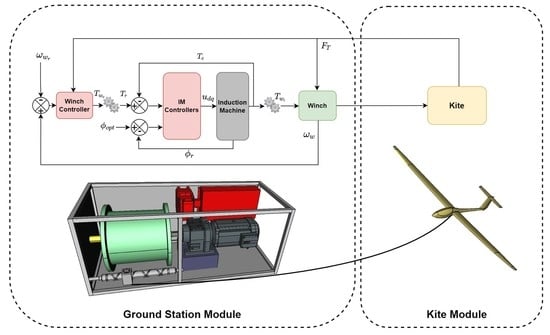
The winch and the IM are coupled using the gear train. In order to avoid the complexity, a linearized interaction is considered between the winch and IM gears (cf. Figure 1). The relationship between the winch and IM torques is given as:

$$\begin{array}{cc}\hfill T_r& ={\displaystyle \frac{N_{{}_{IM}}}{N_w}}{T}_{w_c},\hfill \\ \hfill T_{w_i}& ={\displaystyle \frac{N_w}{N_{{}_{IM}}}}{T}_e.\hfill \end{array}$$

(9)

where $T_r$, $T_{wc}$, $T_{wi}$, $N_{IM}$, and $N_w$ represent reference torque trajectory of IM, torque produced by the winch speed controller, input torque to the winch, number of teeth of IM gear, and number of teeth of winch gear, respectively.

The gears are used to provide a mechanical advantage to IM, so that it can drive a heavier load. To make this possible, a bigger gear is used on the winch side as compared to the IM gear, i.e., $N_w>N_{{}_{IM}}$.

3. Cascade Control Strategy for Ground Station Module

As mentioned earlier, the objective of the GSM is to operate KM at the prescribed velocity, which depends upon the operating phase of an AWES. For this purpose, a winch speed control system is designed to maintain a prescribed speed of the winch during the traction phase. This is only possible by designing a cascade control system as shown in Figure 1. The symbols ${\omega }_{w_r}$, $T_{w_c}$, $T_r$, $T_e$, $T_{w_i}$, $F_T$, ${\omega }_w$, ${\varphi }_r$, ${\varphi }_{opt}$ and $u_{dq}$ represent reference winch velocity, output torque of winch speed controller, reference induced torque of the IM, induced torque of the IM, input torque of the winch, tether force, winch velocity, rotor flux, optimal rotor flux and $d-q$ axes stator control voltages, respectively. The interaction between the winch and IM controllers is made in such a way that the torque provide to the IM (IM acting as a generator) has such a time profile that the desired winch speed can be attained. In Figure 1, the inner loop contains the IM torque controller and the winch speed control system is in the outer loop. As a general rule of thumb, the bandwidth of the inner control loop, i.e., IM control system needs to be 10 times faster as compared to the outer loop for the winch speed control. This is required to ensure that the IM provides the required torque almost instantly, needed to attain the desired winch velocity. As discussed earlier, the interaction between GSM and KM is through the winch, as the tether attached to the kite is wound on the winch. The detail of the IM and winch speed controllers is provided in the subsequent text.

3.1. Sliding Mode Control Design for Winch System

A conventional SMC is designed for the winch model given in (1). The first step in SMC design is the selection of a sliding variable. In order to keep ${\omega }_w$ at the desired value ${\omega }_{w_r}$, a proportional integral (PI) type sliding variable is selected as:

$$\begin{array}{cc}\hfill s& =e_w+\eta {\int }^t{e}_{w}dt,\hfill \end{array}$$

(10)

where $\eta \in {\Re }^{+}$ is a design parameter and $e_w={\omega }_w-{\omega }_{w_r}$ is the winch speed tracking error.

To ensure the finite time convergence of the system trajectories to the sliding manifold the following reachability condition is selected, cf. [43]:

$$\begin{array}{cc}\hfill \dot{s}& =-\kappa sgn\left(s\right),\hfill \end{array}$$

(11)

where $\kappa \in {\Re }^{+}$ represents the discontinuous controller gain.

After computing the time derivative of (10) and substituting in (11), we can obtain the following expression for the output torque ($T_{w_c}=T_{w_i}$) of the winch speed controller.

$$\begin{array}{cc}\hfill T_{w_c}& =-|F_T|r_w+b_w{\omega }_w+J_w\left(-\kappa sgn\left(s\right)+{\dot{\omega }}_{w_r}-\eta e_w\right).\hfill \end{array}$$

(12)

In order to show that the control law given in (12) drags the system trajectories to the manifold $s=0$ in finite time, a Lyapunov functional is selected as follows:

$$\begin{array}{cc}\hfill V& ={\displaystyle \frac{1}{2}}{s}^2.\hfill \end{array}$$

(13)

Taking the time derivative of the Lyapunov functional in (13) along the trajectories of (1), we get:

$$\begin{array}{cc}\hfill \dot{V}& =s\tilde{\dot{s}},\hfill \\ \hfill & =s\left\{{\displaystyle \frac{1}{J_w}}\left(|F_T|r_w-b_w{\omega }_w-d{T}_{w_c}+\zeta \left(t\right)\right)-{\dot{\omega }}_{w_r}+\eta e_w\right\},\hfill \end{array}$$

(14)

where $\tilde{\dot{s}}$ represents the dynamics of the perturbed winch system, including the effect of unknown $\zeta \left(t\right)$.

Now substituting (12) in (14) we get the following expression for $\dot{V}$:

$$\begin{array}{cc}\hfill \dot{V}& =s\left(-\kappa sgn\left(s\right)+{\displaystyle \frac{\zeta \left(t\right)}{J_w}}\right),\hfill \\ \hfill & \le -\left|s\right|\left(\kappa -{\displaystyle \frac{{\zeta }_0}{J_w}}\right),\because \left|\right|\zeta \left(t\right)\left|\right|\le {\zeta }_0,\hfill \\ \hfill & \le -\psi \left|s\right|,\hfill \\ \hfill & \le -\sqrt{2}\psi \sqrt{V},\hfill \end{array}$$

(15)

where $\psi =(\kappa -{\zeta }_0/J_w)\in {\Re }^{+}$ is a design parameter.

According to [44], the result in (15) ensures that the trajectories of the perturbed winch system in (1) converge to the sliding manifold $s=0$ in finite-time ($t_s$), which is characterized as:

$$\begin{array}{cc}\hfill t_s& ={\displaystyle \frac{\sqrt{2V\left(s\right(0\left)\right)}}{\psi }}.\hfill \end{array}$$

(16)

Now, substituting $s=0$ in (10) yields the following dynamics of the sliding mode:

$$\begin{array}{cc}\hfill e_w\left(t\right)& =e_w\left(0\right)exp\left\{-\psi t\right\},\hfill \end{array}$$

which shows that $e_w$ converges exponentially.

3.2. Rotor-Based Field-Oriented Control of Induction Machine

In a separately-excited DC motor, the direction of the armature current is always orthogonal to the main flux. As the main flux is constant, the electromagnetic torque is only dependent on the armature current. Due to the orthogonality, there is no coupling between the main flux and armature current. Therefore, the magnitudes of the field flux and the electromagnetic torque can be controlled independently. Moreover, the instantaneous control of the torque and flux is also possible. This DC motor control concept serves as the basis of the field-oriented control, cf. [39].

Using the conventional $as-bs-cs$ reference frame, the field-oriented control can not be designed, because the stator currents $i_{as}$, $i_{bs}$, and $i_{cs}$ are not orthogonal to each other. Therefore, the first step is to convert the $3-\varphi$ currents to $2-\varphi$ SRRF currents, orthogonal to each other. The next step is to identify the torque and flux producing components from the $2-\varphi$ currents. Generally, the d-axis current is assigned as the flux producing current. Unlike DC motors, both rotor and stator fluxes in an IM are rotating with speed ${\omega }_e$, so, it is mandatory to work with SRRF rotating with the same speed. In this paper, the RFOC-based vector control of IM is designed. Figure 2a shows the alignment of stator current $i_{ds}$ with the rotor flux (${\varphi }_r={\varphi }_{dr}$). Since the field flux only exists on the d-axis, therefore ${\varphi }_{qr}=0$ (cf. Figure 2b) and $T_e$ given in (6) can be re-written as:

$$\begin{array}{cc}\hfill T_e& ={\displaystyle \frac{3N_P{L}_m}{2L_r}}{\varphi }_{dr}{i}_{qs}.\hfill \end{array}$$

(17)

From (17), it can be seen that $i_{qs}$ is the torque producing component of the stator current. Now the DC motor-like control is possible for an IM, where $i_{ds}$ behaves like a field current, which is responsible for producing the main rotor flux ${\varphi }_r$. While $T_e$ is only dependent on $i_{qs}$, which is analogous to the armature current. As both $i_{ds}$ and $i_{qs}$ are orthogonal, $T_e$ and ${\varphi }_{dr}$ can be controlled independently. Furthermore, the instantaneous control of both $T_e$ and ${\varphi }_{dr}$ is also possible.

It can be seen in Figure 2 that ${\varphi }_r$ is completely aligned with the d-axis. Since both the axis and ${\varphi }_r$ rotate with ${\omega }_e$, hence, the d-axis is always locked at the position of ${\varphi }_r$. Resultantly, ${\varphi }_r={\varphi }_{dr}$ and ${\varphi }_{qr}=0$. However, ${\varphi }_r$ has both $d^s-q^s$ axes components, i.e., ${\varphi }_{dr}^s$ and ${\varphi }_{qr}^s$ in SRF, whose magnitudes change with the position of ${\varphi }_r$. From Figure 2b, the position of the rotor flux ${\theta }_e$ can be computed as:

$$\begin{array}{cc}\hfill {\theta }_e& =arctan\left({\displaystyle \frac{{\varphi }_{qr}^s}{{\varphi }_{dr}^s}}\right).\hfill \end{array}$$

(18)

The angle ${\theta }_e$ is very critical in RFOC, as, according to (3), it is used to transform SRF to SRRF and vice versa.

3.2.1. Torque and Flux Controller Design

In this work, two decentralized PI controllers are designed for tracking the desired torque and flux trajectories. The reference trajectory of the torque $T_r$ is generated by the winch speed controller. Whereas, the reference flux ${\varphi }_{opt}$ is the optimal time profile of the flux, which yields the maximum efficiency of IM. PI control-based $d-q$ axes control voltages in SRRF are given as:

$$\begin{array}{cc}\hfill u_{qs}& =k_{p_T}{e}_{{}_T}+k_{i_T}{\int }_0^t{e}_{{}_T}{d}_{{}_{\tau }},\hfill \\ \hfill u_{ds}& =k_{p_{\varphi }}{e}_{{}_{\varphi }}+k_{i_{\varphi }}{\int }_0^t{e}_{{}_{\varphi }}{d}_{{}_{\tau }},\hfill \end{array}$$

(19)

where $e_{{}_T}=T_r-T_e$ and $e_{{}_{\varphi }}={\varphi }_{opt}-{\varphi }_{dr}$ are tracking errors between desired and actual electromagnetic torques and the optimal and actual d-axis rotor fluxes in SRRF, respectively; and $k_{p_j},k_{i_j}$ represent the proportional and integral gains of the PI controllers, respectively.

The optimal flux ${\varphi }_{opt}$, which minimizes the losses in IM is given as (cf. [42]):

$$\begin{array}{cc}\hfill {\varphi }_{opt}& ={\lambda }_{opt}\sqrt{|T_r|},\hfill \\ \hfill {\lambda }_{opt}& =\sqrt{{\displaystyle \frac{L_m}{T_k}}\sqrt{1+{\left({\displaystyle \frac{L_m}{L_r}}\right)}^2{\displaystyle \frac{R_r}{R_s}}}},\hfill \\ \hfill T_k& ={\displaystyle \frac{3N_P{L}_m}{2L_r}}.\hfill \end{array}$$

(20)

From Figure 2b, the rotor flux ${\varphi }_{dr}$ can be computed as:

$$\begin{array}{cc}\hfill {\varphi }_{dr}& =\sqrt{{{\varphi }_{dr}^s}^2+{{\varphi }_{qr}^s}^2}.\hfill \end{array}$$

(21)

It can be seen from (21) that ${\varphi }_{dr}^s$ and ${\varphi }_{qr}^s$ are required to design RFOC. As these fluxes are not measurable, they are estimated using a discrete time Kalman filter (DKF).

3.2.2. Discrete-time Kalman Filter for Flux Estimation

It is desired to estimate ${\varphi }_{dr}^s$ and ${\varphi }_{qr}^s$, therefore, the model given in (8) is employed to design DKF. The rotor speed dynamics in (5) and SRF model in (8) can be combined in the control-oriented form as:

$$\begin{array}{cc}\hfill \dot{x}& =f\left(x\right)+gu,\hfill \\ \hfill x^T& =\left[\begin{array}{ccccc}{i}_{qs}^s& i_{ds}^s& {\varphi }_{qr}^s& {\varphi }_{dr}^s& {\omega }_r\end{array}\right],\hfill \\ \hfill u^T& =\left[\begin{array}{cc}{u}_{qs}^s& u_{ds}^s\end{array}\right],\hfill \\ \hfill g^T& =\left[\begin{array}{ccccc}{k}_4& 0& 0& 0& 0\\ 0& k_4& 0& 0& 0\end{array}\right],\hfill \\ \hfill f\left(x\right)& =\left[\begin{array}{c}-k_1{x}_1+k_2{x}_3-k_3{x}_4{x}_5\\ -k_1{x}_2+k_2{x}_4+k_3{x}_3{x}_5\\ -k_5{x}_3+N_P{x}_4{x}_5+k_6{x}_1\\ -k_5{x}_4-N_P{x}_3{x}_5+k_6{x}_2\\ {\displaystyle \frac{N_P}{J}}\left(T_e-T_L-b{x}_5\right)\end{array}\right],\hfill \end{array}$$

(22)

where $x\in {\Re }^5$ is the state vector; $f\left(x\right)\in {\Re }^5$ represents the nonlinear function of states; $u\in {\Re }^2$ denotes the control input vector and $g\in {\Re }^{5\times 2}$ is the input matrix.

Considering the fact that the stator currents $i_{qs}^s$, $i_{ds}^s$, and ${\omega }_r$ are measurable, the output equation for IM can be written as:

$$\begin{array}{cc}\hfill y& =Cx,\hfill \\ \hfill C& =\left[\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 1\end{array}\right],\hfill \end{array}$$

(23)

where $C\in {\Re }^{3\times 5}$ is the output matrix.

In this work, a linear DKF is designed for the flux estimation, which is based on the following quasi-linear model of the IM:

$$\begin{array}{cc}\hfill \dot{x}& =f\left(x\right)+gu=A^T\left(x\right)x+gu.\hfill \end{array}$$

(24)

The state-dependent matrix $A\left(x\right)$ is given as:

$$\begin{array}{cc}\hfill A\left(x\right)& =\left[\begin{array}{ccccc}|& |& |& |& |\\ a_1& a_2& a_3& a_4& a_5\\ |& |& |& |& |\end{array}\right],\hfill \end{array}$$

(25)

where the columns $a_i\in {\Re }^5$ can be computed as, (cf. [40,45]):

$$\begin{array}{cc}\hfill a_i& =\nabla f_i\left(x\right)+{\displaystyle \frac{f_i\left(x\right)-x^T\nabla f_i\left(x\right)}{x^{T}x}}x,x\ne 0,\hfill \end{array}$$

(26)

where $\nabla f_i\left(x\right)$ is the gradient of the element i of $f\left(x\right)$ in the direction of state vector x and $f_i\left(x\right)$ represents the $i^{th}$ element of $f\left(x\right)$. The gradient of vector field $f\left(x\right)$ is given as:

$$\begin{array}{cc}\hfill \nabla f\left(x\right)& =\left[\begin{array}{ccccc}-k_1& 0& k_6& 0& {\displaystyle \frac{T_k{N}_P}{J}}{x}_4\\ 0& -k_1& 0& k_6& -{\displaystyle \frac{T_k{N}_P}{J}}{x}_3\\ k_2& k_3{x}_5& -k_5& -x_5& -{\displaystyle \frac{T_k{N}_P}{J}}{x}_2\\ -k_3{x}_5& k_2& x_5& -k_5& {\displaystyle \frac{T_k{N}_P}{J}}{x}_1\\ -k_3{x}_4& k_3{x}_3& x_4& -x_3& -{\displaystyle \frac{b}{J}}.\end{array}\right]\hfill \end{array}$$

(27)

The next step is to obtain the discrete-time state-space representation of the SRF model of IM. Therefore, the state equation in (24) is discretized using Euler’s method, with a sample time $T_s$ to obtain:

$$\begin{array}{cc}\hfill x_k& =F_{k-1}+G{u}_{k-1}+w_{k-1},\hfill \\ \hfill y_k& =C_k+v_k,\hfill \end{array}$$

(28)

where $F=I_5+A^T\left(x\right)T_s$, $G=T_{s}g$, and $w_k$ and $v_k$ are white, zero-mean, uncorrelated noise processes with known covariance matrices $Q_k$ and $R_k$, respectively, which are characterized as (cf. [46]):

$$\begin{array}{cc}\hfill & w_k\sim \left(0,Q_k\right),\hfill \\ \hfill & v_k\sim \left(0,R_k\right),\hfill \\ \hfill & E\left[w_k{w}_j^T\right]=Q_k{\delta }_{k-j},\hfill \\ \hfill & E\left[v_k{v}_j^T\right]=R_k{\delta }_{k-j},\hfill \\ \hfill & E\left[v_k{w}_j^T\right]=0,\hfill \end{array}$$

where the kronecker delta function ${\delta }_{k-j}=1$ if $k=j$ and ${\delta }_{k-j}=0$ if $k\ne j$.

By using (28), DKF can be implemented in two steps (cf. [46]):

• The initialization of DKF is carried out as:

  $$\begin{array}{cc}\hfill & {\widehat{x}}_0^{+}=E\left(x_0\right),\hfill \\ \hfill & P_0^{+}=E\left[\left(x_0-{\widehat{x}}_0^{+}\right){\left(x_0-{\widehat{x}}_0^{+}\right)}^T\right],\hfill \end{array}$$

  (29)

  where ${\widehat{x}}_0$ is the initial state estimate, $P_0$ is the initial estimation error covariance matrix, and the superscript ${}^{+}$ denotes a posteriori estimate, which takes into account all the measurements up to time k.
• The main algorithm of DKF comprises the following equations, which are sequentially solved for each time step $k=1,2,\dots$

  $$\begin{array}{cc}\hfill & P_k^{-}=F_{k-1}{P}_{k-1}^{+}{F}_{k-1}^T+Q_{k-1},\hfill \\ \hfill & K_k^{-}=P_k^{-}{C}_k^T{\left(C{P}_k^{-}{C}^T+R_k\right)}^{-1},\hfill \\ \hfill & {\widehat{x}}_k^{-}=F_{k-1}{\widehat{x}}_{k-1}^{+}+G{u}_{k-1},\hfill \\ \hfill & {\widehat{x}}_k^{+}={\widehat{x}}_k^{-}+K_k\left(y_k-C_k{\widehat{x}}_k^{-}\right),\hfill \\ \hfill & P_k^{+}=\left(I_5-K_{k}C\right)P_k^{-}{\left(I_5-K_{k}C\right)}^T+K_k{R}_k{K}_k^T,\hfill \end{array}$$

  (30)

  where K is the Kalman gain and the superscript ${}^{-}$ represents the a priori estimate, which does not consider measurement.

3.2.3. Implementation of RFOC on IM

RFOC architecture for IM is presented in Figure 3. It can be seen that the design of the PI-based torque and flux controllers uses the variables in SRRF, whereas, DKF is designed by using the SRF model. The control voltages $u_{qs}$ and $u_{ds}$ in $d^e-q^e$ are converted to $3-\varphi$$as-bs-cs$ voltages through a series of inverse Park’s and Clarke’s transformations, respectively. Then, $3-\varphi$ set of voltages $u_a$, $u_b$, and $u_c$ are fed into the inverter which eventually drives the IM. On the other hand, the set of measured $3-\varphi$ stator voltages from IM are converted to $u_{qs}^s$ and $u_{ds}^s$ by using Clarke’s transformation (cf. (2)). Based on the measurements and $d^s-q^s$ input voltages, DKF estimates ${\varphi }_{dr}^s$ and ${\varphi }_{qr}^s$ by using the algorithm given in (29) and (30). Then, for the controller design, Park’s transformation (cf. (3)) is used to convert the electrical state variables into SRRF.

The most critical parameter of RFOC is ${\theta }_e$, as it is used for the transformation of SRF to SRRF and vice versa. A wrong estimation of ${\theta }_e$ can cause the malfunctioning of RFOC.

4. Results and Discussions

The concept of AWES presented in Figure 1 is realized using MATLAB and Simulink. The nominal values of the winch and the IM model parameters used for the simulations are given in

Table 1. Nominal parameters of the winch and IM models.

Parameter	Value	Parameter	Value	Parameter	Value	Parameter	Value
$N_p$	2	$R_s$	0.295	$R_r$	0.379	$L_r$	0.0608
$L_s$	0.0608	$L_m$	0.059	J	0.62	b	0.1
$b_w$	0.01	$J_w$	0.124	$r_w$	0.25	$N_w/N_{IM}$	12

.

Some practical considerations and assumptions for the simulation of the traction phase of the AWES are listed below:

• A variable step MATLAB solver: Ode23t is used to simulate the AWES in Figure 1. The minimum and maximum step sizes used for simulation are 5 $\mathsf{\mu }$s and 50 $\mathsf{\mu }$s, respectively.
• The minimum height of the tether from where the KM is launched into the cross wind flight is $L_{min}=50$ m. Whereas, the power production phase is stopped when the tether length reaches its maximum value: $L_{max}=150$ m.
• To evaluate the robustness of the control strategy, it is assumed that the wind gusts generate a constant disturbance torque, i.e., $\zeta \left(t\right)=12.4$ Nm in (1). It is important to mention here that we have not used any specific dynamic model of the wind gust. The constant value for the wind gust used was the maximum value of the disturbance considered, corresponding to the simulation of the worst case scenario.
• The desired angular speed of the winch ${\omega }_{w_r}=10$ r/s for the traction pahse. Positive angular speed refers to counter-clockwise rotation, whereas, negative angular speed indicates clockwise rotation.
• A 5.5 KW IM with rated line-line voltage $u_{LL}=400$ V ($u_{\varphi }=231$ V), operating at 50 Hz is considered for the simulation study. The rated speed, rated torque, and efficiency of the IM are 1461 rev/min (153 r/s), 780 Nm, and $89.6$%, respectively.
• It is assumed that the gain of voltage fed inverter in Figure 2 is unity.
• In order to reduce the chattering, the discontinuous function: $sgn\left(s\right)$ in (12) is approximated by a continuous function: $sgn\left(s\right)\approx tanh(s/\sigma )$, where $\sigma =5\times {10}^{-3}$ is the width of the boundary layer, cf. [43].

The KM of [34] is integrated with the GSM as shown in Figure 1. The orientation of the KM suitable for the traction phase is set by the local on-board controllers. During the cross-wind flight, KM pulls the tether with a large $F_T$ and hence the winch drives the IM, which acts as a generator to produce the electrical power. The trajectory of the KM is shown in Figure 4, which demonstrates the figure-of-eight flight trajectory.

The remaining simulation results are for the cascade control of the GSM. Figure 5 shows that the winch speed controller based on SMC successfully drags ${\omega }_w$ to its desired level ${\omega }_{w_r}$ in the presence of the input disturbance $\zeta \left(t\right)$. Due to the use of gears, the direction of rotation is opposite for the winch and IM. This can be seen in Figure 5 and Figure 6. The control effort $T_{w_c}$ for the winch speed controller is shown in Figure 7. The discontinuous gain of the SMC used for the simulations is $\kappa =150$.

The performance of the field oriented control of the IM is demonstrated in Figure 7 and Figure 8. The tether force $F_T$ exerted on the winch is shown in Figure 9. During the traction phase, $F_T$ drives the IM, which operates as a generator to produce electricity. According to (9) and Table 1, $T_r=T_{wc}/12$ and $T_e=T_{wi}/12$. Therefore, the results in Figure 7 show that the torque controller accurately keeps the induced torque $T_e$ of the IM to the desired level $T_r$. Similarly, the rotor flux ${\varphi }_{dr}$ successfully tracks the optimal flux trajectory ${\varphi }_{opt}$, cf. Figure 8. The electrical angle ${\theta }_e$ in (18), which is used for the transformation from SRF to SRRF and vice-versa is shown in Figure 10. The $2-\varphi$ control voltages of the torque ($u_{qs}$) and flux ($u_{ds}$) PI controllers are shown in Figure 11, and the corresponding $3-\varphi$ control voltages are shown in Figure 12. The proportional and integral gains for the torque and flux PI controllers are $k_{p_T}=100$, $k_{i_T}=6000$, $k_{p_{\varphi }}=100$, and $k_{i_{\varphi }}=6000$, respectively. It can be seen in Figure 7 and Figure 8, that RFOC makes the instantaneous control of both torque and flux possible.

The remaining section qualitatively evaluates the performance of the DKF, which is used to estimate ${\varphi }_{qr}^s$ and ${\varphi }_{dr}^s$. To study the estimation behavior of the DKF, it is necessary to initialize the DKF and actual IM model with different initial conditions. Therefore, the initial conditions for the state variables of the IM model and DKF are given as:

$$\begin{array}{cc}\hfill x_0& ={\left[\begin{array}{ccccc}0.001& 0.001& 0.001& 0.001& 0.001\end{array}\right]}^T,\hfill \\ \hfill {\widehat{x}}_0^{+}& ={\left[\begin{array}{ccccc}2& 2& 0.02& 0.02& 1\end{array}\right]}^T.\hfill \end{array}$$

The initial error covariance matrix in (29) is given as:

$$\begin{array}{cc}\hfill P_0^{+}& =\left[\begin{array}{ccccc}3.9960& 3.9960& 0.0020& 0.0020& 1.9970\\ 3.9960& 3.9960& 0.0020& 0.0020& 1.9970\\ 0.0020& 0.0020& 0& 0& 0.0010\\ 0.0020& 0.0020& 0& 0& 0.0010\\ 1.9970& 1.9970& 0.0010& 0.0010& 0.9980\end{array}\right].\hfill \end{array}$$

The process and measurement noises covariance matrices in (30) are selected as $Q={10}^{-8}\times I_5$ and $R=diag({10}^{-1},{10}^{-1},1)$, respectively. It is pertinent to mention here that the matrices Q and R are selected after a few trials. It can be seen from Figure 13 and Figure 14 that the DKF gives a very good estimate of the unknown SRF fluxes. The DKF uses speed and $d-q$ axes SRF currents of the IM as the measurements to reconstruct the SRF fluxes. The measured and estimated $d-q$ axes currents in SRF are shown in Figure 15 and Figure 16, whereas the measured and estimated IM speed is depicted in Figure 6.

Due to the varying load, the efficiency of the IM is not constant during the traction phase. The dynamic efficiency of the IM ($\eta$) during the traction phase is characterized as (cf. [47]):

$$\begin{array}{cc}\hfill \eta & =100\times {\displaystyle \frac{\frac{3}{2}\left(u_{ds}{i}_{ds}+u_{qs}{i}_{qs}\right)}{T_{w_c}{\omega }_w}}.\hfill \end{array}$$

(31)

The efficiency is depicted in Figure 17. It can be seen from Figure 6 and Figure 17 that $\eta$ is small when ${\omega }_m$ is small and it reaches its maximum value when the IM operates near the rated speed.

5. Conclusions

In this paper, we consider the control architecture of an AWES and propose a controller design for one of its main modules: The ground station module (GSM). We develop a cascade control strategy for the GSM during the traction phase. The design of the cascade control system for the GSM comprises the winch speed controller in the outer loop and the torque controller of the induction machine (IM) in the inner control-loop. The integral sliding mode control (SMC) technique is used to design the winch speed controller, whereas, the IM torque control is based on rotor flux oriented control (RFOC) and is implemented with decentralized PI controllers for induced torque and for rotor flux. To enable the implementation of RFOC, a discrete Kalman filter is used to estimate the unknown states of the IM.

The performance of the proposed controllers is evaluated through simulations carried out in Matlab/Simulink. The simulator includes not only the GSM models and controllers here developed, but also known models and controllers of the KM, enabling the analysis of the overall AWES. The simulation results show that the AWES achieves the desired performance, even in the presence of external bounded disturbances, possibly representing wind gusts.

A major conclusion is that an advanced control strategy for the GSM is key for the successful operation of the overall AWES. The results presented in the paper can serve as motivation for the AWES community to provide further attention to the control of the GSM, which has been much less discussed in the literature than the control of the KM.

One of the possible future extensions of this work is the design of a robust field-oriented control for the IM, such that its performance, efficiency, and aging can be optimized during unsteady state operation. Such extension would contribute in several dimensions to the real-time implementation of the GSM control system.