1. Introduction
Microgrids are a self-sufficiency power system that produces and consumes energy bounded in the system itself. The system is composed of distributed generations, energy storage systems, load, and small-scale networks. It is suggested as a solution to the technical, economical, and environmental problems of the conventional system [
1]. Currently, extensive studies on distributed generations, including operation, control, and protection, are underway [
2,
3]. Among them, maintaining the stability of microgrids, in particular, is still a challenging issue, and studies have been actively conducted to improve the stability using various methods and means [
4,
5]. In microgrids, the power output of the most distributed generation depends on the natural environment, so the diesel synchronous generator (SG) is currently covering up the shortage of energy [
6]. To overcome the vulnerability of microgrids’ stability, it is essential to take advantage (e.g., rotational inertia, reactive power supply, voltage support, and durability of the machine) of the SG and to improve the limit in synchronization.
Microgrids have already become a trend in power systems, and new microgrids are emerging as the number of distributed generations increases. The stability of the SG in the microgrids is a prerequisite for them to be freely connected (or islanded from) to utilities. Therefore, with the aim of improving microgrid stability, we design a research on power system stabilizers (PSS) to improve the stability of SGs. Although SGs play a very important role in microgrids, few PSSs have been studied that are suitable for use in microgrids. It is no doubt that generic PSSs can be used in microgrids that can only operate as utility-connected operation. However, they are not recommended to be used because of the network topology changes in microgrids. Therefore, based on the various studies dealing with the existing PSSs, we conduct a study on a novel PSSs that can achieve the best performance in structural changing systems by considering the characteristics of microgrids. The main objectives and directions of this study are summarized as follows.
As microgrids can change the network configuration of the system, a novel PSS should be able to cope with this structural change.
A novel PSS should be able to help the SG to maintain the synchronizing continuously, even in various disturbances such as the transition to islanded operation or failure of the power system.
A novel PSS should further enhance the damping torque for low-frequency oscillations (LFOs), which is the basic role of a PSS. The power system stabilizer (PSS) was developed to prevent amplification of low-frequency oscillations (LFOs) by the high-gain excitation system of the SG. The lead-lag compensation-based PSS has been most widely used to date because it is robust and it is easy to verify its performance [
7]. In addition, almost all of the control systems of SGs currently operating in the power system are based on linear controllers, so parameters can be set in cooperation with other controllers, and therefore, they are suitable to be applied for large power systems. A PSS supplies electrical torque in phase with the rotor speed deviation to damp out LFOs at which the SG is most vulnerable, thus playing the most significant role in the stability of the SG. However, ensuring robustness for parameter setting and input signals is very important since the fact that a PSS can attenuate vibrations also means that it can produce the opposite effect. In other words, if it were to resonate with other control systems, it might have fatal consequences on the stability of the SG [
8]. Therefore, many studies have been conducted on extracting the pure oscillation of the rotor from the input signals. As a result, PSSs with various input structures have been proposed. In [
9], PSS design structures, review of the classifications of power system oscillation modes, and their effects on a PSS are analyzed. PSS-2B and PSS-4B are assessed from the point of view of their relative performance in tackling a wide range of system problems in [
10]. Liu et al. propose a parallel high-pass component in a PSS for enhancing the phase characteristic of the exciter PSS [
11]. In [
12], two trade-offs in the effectiveness of automatic voltage regulators (AVRs) and PSSs are investigated. As a result of these studies, many defects have been supplemented accordingly.
Besides, a number of studies on PSSs have been conducted in the search for optimal parameters, taking into account the power systems and the SG to be applied. Since phase compensation characteristics play a dominant role in the PSS, parameter tuning determines the performance of the PSS.
In conventional tuning of a PSS, the general tuning guide that still is being used widely is proposed [
13,
14,
15]. In [
16], Gurrala et al. develop a method of designing a fixed-parameter decentralized PSS for interconnected multi-machine power systems. In [
17], an advanced method of [
16] for designing PSS parameters is suggested by proposing a synthesized equivalent bus using local measurements available at the power station. The advantage of the method following the tuning guide is that it is easy to find the general parameter. However, it is impossible to set clear criteria, so it should be dependent on the engineers’ experience and the competence of those who perform the tuning. In addition, there is a disadvantage of not considering all the situations, because a linearized model with limited operating points is used. To overcome these shortcomings, a method of utilizing various heuristic optimization techniques has been proposed. In [
18], Movahedi et al. presented a method of parameter tuning of the flexible AC transmission system (FACTS) and a PSS using various heuristic optimization algorithms (HOAs). In [
19], the performance of particle swarm optimization (PSO) and genetic algorithm (GA) are compared for design problems. In [
20], a new design procedure for simultaneous coordinated designing of a PSS in a multi-machine power system is demonstrated. Shayeghi et al. propose a tuning methodology for PSSs based on the use of PSO that works for systems with 10 or even more machines [
21]. To coordinate the dual action of both static synchronous series compensator (SSSC) and PSS devices, a GA tuning controller is applied in [
22]. In [
23], a mixed objective function consisting of routine eigenvalue stability and nonlinearity indices is proposed and the nonlinear power system response to fault scenarios under various load conditions is optimized using an HOA. As the objective function determines the performance, various objective functions and methods have been proposed in [
7,
21,
23], and formulating an objective function is still a challenging task.
The effects of a PSS have been analyzed. Aderibole et al. [
24] investigate the oscillatory mode of multi-microgrids and analyze the effects on the performance of a PSS. In [
25], Alaboudy et al. analyze the stability characteristics, depending on the system components of the microgrids after a large disturbance occurs. In [
26,
27], a number of issues concerning the stability of microgrids are summarized, studied, and compared with traditional power systems.
Studies to improve the stability of microgrids include applying machine learning techniques to operating prediction and probability-based systems and applying traditional methods such as control-theory-based distributed and cooperative control and energy storage system utilization methods. Recently, machine learning techniques have been applied to various fields, especially when learning time-series data, long short-term memory (LSTM), which is quite effective in long-term memory, has been used for load forecasting [
28,
29]. In [
30], dynamic learning techniques applied to natural networks and population-based algorithms are also applied to the power prediction field for new and renewable sources.
In the case of renewable energy sources that are closely related to the weather, studies have been conducted using power output prediction by linking data acquired from the weather sensors with machine learning [
31,
32]. These methods are utilized in the operation and scheduling of energy storage devices to assist in stable system operations. Furthermore, a failure detection method using various machine learning techniques is proposed in [
33,
34]. Mehdi et al. analyze various detection methods as well as advantages and disadvantages of islanding fault detection [
35]. These methods can contribute to improving the stability of microgrids in conjunction with protection relay. To overcome the low inertia of microgrids, the methods of utilizing virtual synchronous machines and an energy storage device are proposed in [
36,
37]. In addition, a study on the drop control technique of distributed power for frequency and voltage maintenance is carried out in [
38], and Baneshi et al. propose a method to ensure that load fluctuations are efficiently shared by distributed generations [
39].
The remainder of the paper is organized as follows.
Section 2 deals with the characteristics of microgrids and the primary considerations when applying a PSS to microgrids. The theoretical basis of the proposed PSS and the establishment of a control strategy are addressed in
Section 3. In
Section 4, the structural features of the proposed PSS and the overall structure and added functions are described. In
Section 5, before comparing the proposed PSS with the generic PSS and verifying it, the content of objective tuning is included to identify performance differences due to structural characteristics. In
Section 6, small-signal stability analysis is performed using a linearized model to determine the characteristics and performances of the proposed PSS. In
Section 7, the impact on transient stability is investigated by time-domain simulation (TDS), and the performance of the proposed PSS is verified comprehensively through a case study.
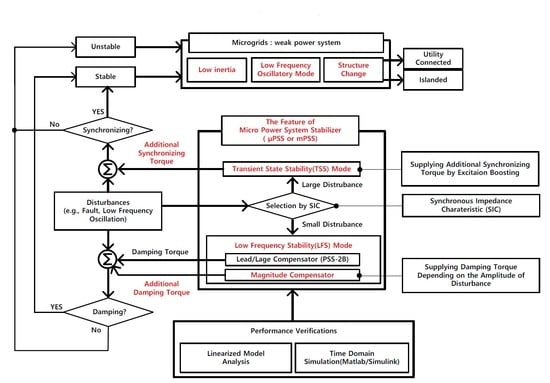
3. Proposed Power System Stabilizer for Stability Enhancement in Microgrids
A micro-power system stabilizer (PSS) is designed to cope with structural changes in the microgrid, provide damping torque to low-frequency oscillations, improve the transient stability by supplying synchronizing torque under large disturbances. It also has the ability to automatically switch into low-frequency stabilizing (LFS) mode and transient state stabilizing (TSS) mode, depending on the amplitude of the SG’s swing.
As mentioned in
Section 2, detection of the operating mode is necessary to cope with the variable structural characteristics of the microgrid. To detect the islanded operation, a method that relies on auxiliary signals, such as on/off contacts of a circuit breaker, is not suitable for distributed control and is not desirable for use due to concerns originated from the loss of the state signals. A suitable signal to add to the PSS is the frequency of the power system (i.e., microgrid frequency (MGF)). If the microgrid frequency is used as an input value, the additional signal plays a little role because the microgrid frequency is almost constant when the microgrid is in utility-connected operation mode. However, in the case of islanded operation, the added frequency signal is the target frequency for which the PSS provides damping torque as a criterion for the change in the rotational speed of the generator, as defined in the non-stiff system swing equation (Equation (8)), because frequency variation depends on the inertia of the microgrid in question.
The microgrid frequency can be easily obtained through a potential transformer, and the excitation system is always monitoring the voltage, so no additional devices are required. Therefore, adding the frequency signal of the power system to the input signal of the PSS enables enhancing the performance of the PSS to be enhanced regardless of the microgrid’s operation mode.
3.1. The Effects of Adding a Microgrid Frequency Signal to the Input of the PSS
When a disturbance occurs in the microgrids in islanded mode, the system frequency and the rotational speed of the SG change. A
PSS attenuates frequency variation because it damps an oscillation corresponding to a difference between two frequencies and performs phase compensation. To analyze the effects of using a microgrid frequency as an input, the following generator-exciter-PSS (GEP) model is used to analyze the damping effect by comparing the output differences depending on the two types of inputs.
If the PSS sufficiently compensates for the phase delay in the SG and the excitation system, the
becomes pure damping torque. In such a case, the characteristic equation of the SG is shown as follows [
41]:
As shown in the above results, adding the frequency signal of the microgrid to the input of the PSS causes , which can improve the damping ratio (ξ) and cope with the system’s inertia changes when the operation mode of microgrids is changed.
3.2. Low-Frequency Stabilizing Mode
The general shape of the frequency characteristic applies to any synchronous machine [
8]. The effective inductance is equal to the synchronous inductance,
, at a frequency less than 0.2 Hz; the transient inductance,
, in the range 0.2 Hz to 2 Hz; and the sub-transient inductance,
, 10 Hz or more. The characteristic of
can be expressed as the Equation (17) and
Figure 2.
Since synchronous impedance is the same as the transfer impedance between the SG and the power system, frequency variation causes impedance changes and affects the power output, , depending on Equation (1). This causes the perturbation of the rotor of the SG (i.e., swing), and the magnitude of the swing is determined in accordance with . Given these characteristics, in a PSS, the magnitude of the stabilization signal, can be controlled according to the magnitude of the perturbation (i.e., the required damping torque by the PSS) that should be compensated according to the frequency of vibration, thereby maximizing the effect of the oscillation damping.
The effect of a change in synchronous impedance on the SG’s power output is:
When the generator power output differentiates concerning synchronous impedance, the correlation between synchronous impedance and the SG output deviation, Equation (19), can be obtained. Converting the torque of Equation (1) into effective power, we get the following:
The partial derivative of Equation (20) by synchronous impedance,
, is Equation (21), and substituting Equation (19) for Equation (21), the relation between the angular acceleration and the synchronous impedance, Equation (22), can be achieved.
To replace the angular acceleration caused by the deviation of synchronous impedance with the acceleration torque of the rotor, from the swing equation (Equation (1)), we get
Then, multiplying Equation (22) by Equation (23), chain rule,
The relationship between the synchronous impedance variation and the acceleration torque can be obtained, as shown in the following:
Using the frequency characteristic of the SG (Equation (17)), the deviation of synchronous impedance (i.e., synchronous impedance characteristic) is obtained:
Substituting Equation (27) for Equation (25) results in a correlation Equation (28) of acceleration torque with respect to the variation of frequency.
Applying Equation (28) as a control law of the magnitude compensation in the PSS can cancel out the acceleration torque generated by the frequency variation. In other words, the damping torque in the range of electro-mechanical mode can be selectively enhanced by compensating the magnitude of the SG’s swing or oscillation as well as phase compensation according to frequency variation, which is the fundamental function of the generic PSS. By adding a magnitude compensator (MC) to the generic PSS for configuring the controller, we can obtain the transfer function of the micro-power system stabilizer (Equation (29)) as follows:
where
: magnitude compensator,
: generator active power output,
: synchronous impedance characteristic,
: washout block, and
: phase compensator (i.e., lead-lag compensator).
It is a structure in which the input (i.e., frequency signal) is compensated by the MC after being filtered to a range of the selective frequency by the washout block of the transfer function (Equation (29)), and the signal is compensated through the lead-lag compensator to perform the phase compensation.
3.3. Transient State Stabilizing Mode
The transient state stabilizing (TSS) mode is added to prepare for large disturbances such as power system faults. This is based on the Lyapunov energy function, which is utilized for enhancing the transient stability of the SG [
41,
42,
43,
44]. The TSS control determines whether to perform an excitation boosting (EB) control, depending on the severity of disturbances. The EB provides instantaneously additional voltage of the charged capacitor to the field circuit, and this control strategy has been established and validated in [
45,
46]. Based on the EB control strategy, it integrates with the μPSS, considering the characteristics of microgrids.
3.3.1. Construction of the TSS Control Law
From [
46], the Lyapunov energy function of the power system is defined as follows:
The rotor angle,
, and speed,
are:
where the net internal mechanical power,
, is expressed as a function of the mechanical power,
, the network equivalent shunt conductances,
, and the voltage behind the transient reactance,
:
In the controlled system,
To modify the above Equation (33) to fit the features of the microgrid, we redefine variables using the following
Figure 3.
of the other SG of the power system can be seen equivalent to
of the microgrid, and the transfer admittance is equal to the equivalent admittance,
, between the internal electromotive force,
, of the SG and the microgrid voltage,
.
of Equation (31) is the calculated value of
of the
i-th SG measured using the phasor measurement unit (PMU) and the wide-area measurement system (WAMS). The microgrid is a distributed control system based on the plug-and-play concept, and it is desirable not to use additional communication devices. It is advantageous to utilize the frequency of the generator terminal voltage through the potential transformer (PT) rather than calculating the center of inertia using the WAMS. Therefore,
and
signals are replaced by
and
, which do not require networks (e.g., WAMS), as shown below.
Using Equations (34) and (35) in Equation (33), we have
Therefore, if Equation (36) is negative, the system can go back to the equilibrium point. When the system voltage drops under large disturbances, the power system will have the following conditions:
Because the microgrid’s admittance is relatively insignificant compared to the synchronous impedance, the following conditions are established:
Therefore, the SG can return to the equilibrium point under the Lyapunov energy function if
is maintained until the following conditions are met:
The control strategy to satisfy the above conditions in TSS mode can be established as follows:
TSS mode is a method of momentarily injecting the booting voltage directly into the field circuit bypassing the AVR circuit. TSS mode determines the injection period, starting point, and end point by Equation (40). Some circuit modifications and installation of additional facilities are required, as additional capacitance and switches need to be configured. It can increase the synchronizing power strongly due to a momentary increase in the field voltage, which also improves the transient stability.
TSS mode should be used in a very limited manner, as features that directly affect the field voltage have an enormous impact on the stability of the SG. The method in [
46] calculated the center of inertia (COI),
, in real time using the WAMS and improved the accuracy of EB motion through the relative generator speed,
, for
. In a
PSS,
does not have the exact same value as
, so it can affect the selectivity of the EB action according to Equation (36). Therefore, to overcome some of the deficient selectivity, a synchronous impedance characteristic (SIC) is used to provide highly reliable selectivity so that LFS and TSS modes can operate and coexist depending on the circumstances facing the situation of the SG, as will be described in
Section 3.4.
3.3.2. The Specifications of Boosting Capacitance
Boosting capacitance (BC) is modeled as an ideal capacitor whose voltage,
, is determined by the maximum field voltage that the rotor can withstand with a security margin [
46]. Given the maximum allowable field voltage (limited by the rotor winding insulation),
, the DC ceiling voltage (maximum DC voltage produced by the rectifier),
, and the generator terminal voltage,
, the capacitor voltage are determined as:
Within the allowed insulation of the field circuit, setting the maximum operating hours,
and
, offers
of the BC.
3.4. Mode-Switching Condition: LFS ← Selection → TSS
Generally, damping torque is enhanced by the PSS, but synchronizing torque could be reduced in part [
12]. To overcome these shortcomings, a
PSS needs to have appropriate transitions between modes so that it can operate in LFS mode in the range of low frequency and in TSS mode in transient conditions under large disturbances. A
PSS can take advantage of the high-gain excitation system and overcome shortcomings by increasing synchronizing torque through the TSS and the supply of damping torque through the LFS. For the two modes to coexist, the synchronous impedance variation (i.e., SIC) of the SG is used as the mode selection signal. Because the deviation in synchronous impedance is proportional to the disturbance’s size, this signal can be used to ensure that the
PSS operates in the appropriate mode, depending on the situation in the microgrid.
Synchronous impedance is an electro-magnetic phenomenon that can be modeled as impedance, which is changed by the variation of the rotational speed of the SG. Frequency characteristics of synchronous impedance can be obtained with the machine’s parameters [
8], which can be used to estimate the amplitude of the swing. These synchronous impedance frequency characteristics can be used as the basis for switching between TSS mode, which increases synchronizing torque for transient stability, and LFS mode, which provides LFOs with damping torque.
5. Tuning the Parameters of the PSS for Verifications
The PSS compensates for the phase delay caused by the characteristics of the excitation system and field circuit through lead-lag compensators. The parameter is a critical factor in determining the PSS’s performance, because the inaccurate parameter can amplify the generator’s rotational oscillations. Therefore, it is necessary to select a more objective tuning method for parameters to accurately identify and verify the performance, characteristics, and effects of the PSS proposed in this paper.
The PSS consists of parameters in PSS-2B: the SIC, MC, and TSS. Because the SIC, MC, and TSS are dependent parameters determined by the characteristics of the SG, the tuning of the PSS can be performed in the same way as that of PSS-2B.
The tuning methods of a PSS typically include the traditional one [
49,
50] that is performed by the procedure of the guide using the analytical technique of control theory and one that utilizes the heuristic optimization algorithm (HOA) that is used in various fields [
7,
20,
21,
22,
23,
24]. It is judged that utilizing heuristic optimization based on algorithms that perform objective function optimization would be more suitable for the performance verification of the
PSS than traditional methods, which are often influenced by the experience, ability, and intuition of the engineer. Therefore, the tuning of the
PSS will be performed through particle swarm optimization (PSO), which is widely used as a PSS parameter-tuning method due to its outstanding performance among HOAs [
2,
18]. The objective function of PSO is the following Equation (43), which is widely used in PSS tuning, and the parameter of the objective function is set up as
Table 3 and using the D-shaped sector in
Figure 5 [
21,
23].
PSO optimizes the parameters of the PSS so that the worst pole and damping ratios of the single-machine non-stiff bus (SMNB) model, which is linearized by 10 operating points (see
Table A1), have values in the predefined range of the D-shaped sector. To utilize PSO for tuning, the setup for the optimization algorithm is required, and the relevant settings are summarized in the table.
The optimization follows the procedure described in the Figure 7a flowchart, and 10 operating points of the SG are listed in
Table A1. To perform optimization using PSO, linearized models of the SG and power systems are needed. Heffron-Philip’s model (HP model,
Figure 1) is widely known as the K-constant model (i.e., SMIB) and has been used in a number of studies on PSS design [
13,
14,
15,
41,
49,
50]. The HP model, a representative one of the stiff voltage system, may be suitable for tuning the gPSS used in large power systems, but it is necessary to consider the effects of bus voltage fluctuations in tuning the parameters of the
PSS, which is operated in microgrids.
A single-machine non-stiff bus (SMNB) is a model that considers changes in the magnitude and phase of the connected power system voltage and is used to make up for the shortcomings of a conventional K-constant model [
16,
17]. Therefore, the use of the SMNB model (see
Figure 6) could consider the effects of the weak system in parameters of the μPSS, so PSO is performed with the model.
Parameters optimized through PSO are listed in
Table 4. As shown in
Figure 7b, the value of the objective function is converged at the minimum by the PSO algorithm. In
Section 7, we will validate these parameters by comparing and analyzing a PSO-optimized PSS (PSO-PSS), typical parameters of a PSS (T-PSS), and the case of an SG without a PSS (w/o PSS).
8. Conclusions
This paper aims to enhance the stability of microgrids by supplementing and improving the gPSS in accordance with the features of microgrids, including structural features, low inertia, and operation mode changes (e.g., islanded or utility-connected mode). By adding the MGF, the PSS could show real ability over the LFOs regardless of microgrids’ structure changes (e.g., islanded or utility-connected mode). In addition, the MC, mode selection, and TSS are included in the PSS. By exerting change, the PSS could effectively damp out LFOs through the MC in LFS mode and supply synchronizing torque to maintain the stability of the SG by TSS, which is selected by the SIC, depending on the type of oscillation and disturbances. The highlights of the μPSS proposed in this paper are as follows:
We propose that adding an MGF to PSS input signals can guarantee the performance of the PSS in microgrids (i.e., systems with changing networks of the power system). The weakness of the PSS is made up for in low-inertia power systems because the perturbation of the power system is considered in the input signal of the PSS by the MGF. SGs operating in microgrids do not have large capacities, but they have a large proportion of relative capacity (e.g., compared to the generation capacity of the entire power system). Therefore, the swing of this SG is closely related to the system frequency variation. In other words, as the perturbation of the SG causes changes in the frequency of the power system, the deviation of speed, the signal used by the gPSS, is valid for large power systems with almost constant frequency of the power system, but not for microgrids. In case study #1, differences depending on whether an MGF is applied or not are clearly identified. In case study #3, the gPSS without an MGF shows that the oscillation does not attenuate but persists until the end of the simulation. The oscillation persists even longer than that without a PSS. These results demonstrate the linkage characteristics of the frequencies between the microgrid and the SG and the validity of the MGF.
In LFS mode, the effects on MCs can be seen through frequency characteristic analysis of the linearized models (i.e., GEP and SMNB models). Differences in frequency characteristics of the GEP model by the MC are demonstrated in
Figure 9 through the Bode diagram analysis.
The
Table 5 summarizes the main features of the Bode analysis, showing that there is no significant change in the actual phase characteristics (some improvements) but an improvement in the magnitude of the key areas (0.01–10 Hz) that the PSS of the SG should be able to compensate. In other words, comparing the phase and magnitude frequency characteristics of the μPSS with those of the gPSS, it can be determined that in the case where the μPSS is applied, the performance has improved in all areas requiring damping torque supply by the PSS.
It is confirmed in
Figure 9 that the poles of the electro-mechanical mode move further to the left side in the s-plane. In particular, the
Table 6 shows an average 31.7% increase in damping torque, thereby mitigating overshooting. The analysis results show that the damping performance for LFOs is enhanced by the novel structures (MC and SIC) that are added to the μPSS proposed in this paper.
In TSS mode, the excitation Boosting (EB) control is performed through the Lyapunov energy-function-based control strategy to provide additional synchronizing power during large disturbances. TSS mode helps to maintain continuous synchronization in cases where the microgrids undergo failure or significant load changes (e.g., transition to islanded operation, tripping a part of the system, etc.). The
Table 7 summarizes the results of a case study to check the effectiveness of the TSS, which shows that the CCT is improved and the allowable load change in the microgrid is increased. Simulation results show that the initial deviation of the phase angle caused by sudden load changes is suppressed by the TSS in
Figure 13.
However, even if the initial phase angle deviation is suppressed by the TSS, it will inevitably exceed the permissible limit of the phase angle between the COI and a generator if the load change eventually becomes unaffordable for one SG. Thus, the initial phase angle difference immediately after load change is suppressed, as in
Figure 13. Then the phase difference exceeds the permissible limit of the angle difference in the end. However, it can be inferred that if proper load sharing is possible among other power sources that can adjust power output, it will converge to a stable system later by appropriately sharing the load if only the initial phase angle deviation of the disturbance is endured by the TSS in a SG.
Parameters play a very important role in the performance of a PSS, so in this work, we perform parameter setting using an HOA, particle swarm optimization, to minimize the impact of parameters when comparing the μPSS with the gPSS. That is because we want to focus on the characteristics caused solely by structural differences between the μPSS and the gPSS. The parameter values found using PSO are applied identically to the test target PSSs (i.e., μPSS and gPSS) to verify the superiority of the μPSS with frequency-domain analysis and TDS. Therefore, in this paper, the test results have nothing to do with the parameters of the PSS. In addition, the μPSS has the advantage of being able to be applied by the good tuning methods proposed in many studies, as its structure is the most widely used one based on PSS-2B.
The SG is not only at the core of a conventional power system, but it also plays a crucial role in microgrids. The PSS is expected to contribute significantly to stability enhancement of the microgrids.