Experimental and Numerical Study on Thermal Hydraulic Performance of Trapezoidal Printed Circuit Heat Exchanger for Supercritical CO2 Brayton Cycle
Abstract
:1. Introduction
2. Experimental System and Method
2.1. Experimental System
2.2. Test PCHE Prototype
2.3. Calculation Method and Uncertainty
2.3.1. Heat Transfer Coefficient
2.3.2. Heat Recovery Efficiency
2.3.3. Pressure Drop Loss and Friction Factor
2.4. Uncertainty Analysis
3. Results and Analysis
3.1. Heat Transfer Performance
3.1.1. Overall Heat Transfer Coefficient
3.1.2. Average Convective Heat Transfer Coefficient
3.2. Heat Recovery Efficiency and Pressure Drop
4. Simulation Verification
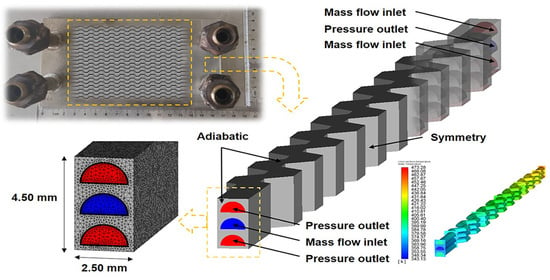
4.1. Model and Mesh
4.2. Verification with Experimental Results
4.3. Low Reynolds Number Expansion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviation | |
| sCO2 | Supercritical carbon dioxide |
| PCHE | Printed circuit heat exchanger |
| HTHF | High-temperature helium test facility |
| Probability density function | |
| KAIST | Korea Advanced Institute of Science and Technology |
| KAIST-HXD | A PCHE design code developed by KAIST |
| NACA | National Advisory Committee for Aeronautics |
| CFD | Computational Fluid Dynamics |
| Roman alphabet | |
| A | Total heat transfer area, m2 |
| d | Hydraulic diameter of the semicircle, m |
| f | Friction factor |
| H | Enthalpy, kJ/kg |
| h | Average convective heat transfer coefficient, kW/(m2·K) |
| k | Thermal conductivity of 316 L, W/(m·K) |
| l | Length of trapezoidal channel, m |
| m | Mass flow rate, kg/s |
| Nu | Nusselt number |
| Pr | Prandtl number |
| ΔP | Pressure drop, kPa |
| Q | Heat transfer rate, kW |
| Re | Reynolds number |
| r | Thermal resistance |
| T | Temperature, °C |
| ΔT | Log-mean temperature difference, °C |
| U | Overall heat transfer coefficient, kW/(m2·K) |
| u | Mean velocity, m/s |
| uR | Uncertainty of an indirect measurement |
| ux | Uncertainty of a direct measurement |
| Greek symbols | |
| δ | Average heat conduction thickness, m |
| η | Heat recovery efficiency |
| λ | Average thermal conductivity of fluid, W/(m·K) |
| μ | Mean viscosity, Pa·s |
| ρ | Mean density, kg/m3 |
| Subscripts | |
| c | Cold side value |
| h | Hot side value |
| in | Inlet value |
| out | Outlet value |
| ave | Average value |
| wall | Channel wall value |
| fluid | Fluid value |
| mid | Middle value between hot and cold channels |
| Ph | Hot-side pressure value |
| Pc | Cold-side pressure value |
| core | Heat transfer core |
| total | Measured |
| pipes | Pressure drop in pipes |
| tube fittings | Pressure drop in tube fittings |
| elbows | Pressure drop in elbows |
| diversion areas | Pressure drop in diversion areas |
| trapezoidal | Pressure drop of trapezoidal prototype |
| single-plate | Pressure drop of single-plate prototype |
| straight | Pressure drop in straight channel |
| i | Number of the direct measurement |
| w | Thermal conduction resistance in wall |
| s | Fouling resistance |
References
- Mylavarapu, S.K.; Sun, X.; Glosup, R.E.; Christensen, R.N.; Patterson, M.W. Thermal hydraulic performance testing of printed circuit heat exchangers in a high-temperature helium test facility. Appl. Therm. Eng. 2014, 65, 605–614. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Y.; Zhang, L.; Yao, M.; Kruizenga, A.; Anderson, M. PDF-based modeling on the turbulent convection heat transfer of supercritical CO2 in the printed circuit heat exchangers for the supercritical CO2 Brayton cycle. Int. J. Heat Mass Transf. 2016, 98, 204–218. [Google Scholar] [CrossRef]
- Chen, M.; Sun, X.; Christensen, R.N.; Shi, S.; Skavdahl, I.; Utgikar, V.; Sabharwall, P. Experimental and numerical study of a printed circuit heat exchanger. Ann. Nucl. Energy 2016, 97, 221–231. [Google Scholar] [CrossRef] [Green Version]
- Shin, C.W.; NO, H.C. Experimental study for pressure drop and flow instability of two-phase flow in the PCHE-type steam generator for SMRs. Nucl. Eng. Des. 2017, 318, 109–118. [Google Scholar] [CrossRef]
- Chu, W.; Li, X.; Ma, T.; Chen, Y.; Wang, Q. Experimental investigation on SCO2-water heat transfer characteristics in a printed circuit heat exchanger with straight channels. Int. J. Heat Mass Transf. 2017, 113, 184–194. [Google Scholar] [CrossRef]
- Xu, A.; Huang, Y.; Wang, J. An experimental study on a straight-channel printed circuit heat exchanger for supercritical CO2 power cycle applications. In Proceedings of the 2018 26th International Conference on Nuclear Engineering (ICONE26), London, UK, 22–26 July 2018. ICONE26-81588. [Google Scholar] [CrossRef]
- Park, J.H.; Kwon, J.G.; Kim, T.H.; Kim, M.H.; Cha, J.; Jo, H. Experimental study of a straight channel printed circuit heat exchanger on supercritical CO2 near the critical point with water cooling. Int. J. Heat Mass Transf. 2020, 150, 119364. [Google Scholar] [CrossRef]
- Arslan, F.; Guzel, B. Numerical and experimental thermal-hydraulic performance analysis of a supercritical CO2 Brayton cycle PCHE recuperator. Arab. J. Sci. Eng. 2021, 46, 7543–7556. [Google Scholar] [CrossRef]
- Nikitin, K.; Kato, Y.; Ngo, L. Printed circuit heat exchanger thermal–hydraulic performance in supercritical CO2 experimental loop. Int. J. Refrig. 2006, 29, 807–814. [Google Scholar] [CrossRef]
- Kim, I.H.; No, H.C.; Lee, J.I.; Jeon, B.G. Thermal hydraulic performance analysis of the printed circuit heat exchanger using a helium test facility and CFD simulations. Nucl. Eng. Des. 2009, 239, 2399–2408. [Google Scholar] [CrossRef]
- Kim, I.H.; No, H.C. Thermal hydraulic performance analysis of a printed circuit heat exchanger using a helium–water test loop and numerical simulations. Appl. Therm. Eng. 2011, 31, 4064–4073. [Google Scholar] [CrossRef]
- Kim, I.H.; No, H.C. Thermal–hydraulic physical models for a printed circuit heat exchanger covering He, He–CO2 mixture, and water fluids using experimental data and CFD. Exp. Therm. Fluid Sci. 2013, 48, 213–221. [Google Scholar] [CrossRef]
- Baik, S.; Kim, S.G.; Bae, S.G.; Ahn, Y.; Lee, J.; Lee, J.I. Preliminary experimental study of precooler in supercritical CO2 Brayton cycle. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition (GT2015), Montréal, QC, Canada, 15–19 June 2015. GT2015-42915. [Google Scholar] [CrossRef]
- Dai, Z.; Zheng, Z.; Fletcher, D.F.; Haynes, B.S. Experimental study of transient behaviour of laminar flow in zigzag semi-circular microchannels. Exp. Therm. Fluid Sci. 2015, 68, 644–651. [Google Scholar] [CrossRef]
- Bae, S.J.; Kwon, J.; Kim, S.G.; Son, I.; Lee, J.I. Condensation heat transfer and multi-phase pressure drop of CO2 near the critical point in a printed circuit heat exchanger. Int. J. Heat Mass Transf. 2019, 129, 1206–1221. [Google Scholar] [CrossRef]
- Zhou, J.; Cheng, K.; Zhang, H.; Liu, B.; Huai, X.; Guo, J.; Zhang, H.; Cui, X. Test platform and experimental test on 100 kW class printed circuit heat exchanger for supercritical CO2 Brayton cycle. Int. J. Heat Mass Transf. 2020, 148, 118540. [Google Scholar] [CrossRef]
- Cheng, K.; Zhou, J.; Zhang, H.; Huai, X.; Guo, J. Experimental investigation of thermal-hydraulic characteristics of a printed circuit heat exchanger used as a pre-cooler for the supercritical CO2 Brayton cycle. Appl. Therm. Eng. 2020, 171, 115116. [Google Scholar] [CrossRef]
- Cheng, K.; Zhou, J.; Huai, X.; Guo, J. Experimental exergy analysis of a printed circuit heat exchanger for supercritical carbon dioxide Brayton cycles. Appl. Therm. Eng. 2021, 192, 116882. [Google Scholar] [CrossRef]
- Zhang, H.; Cheng, K.; Huai, X.; Zhou, J.; Guo, J. Experimental and numerical study of an 80-kW zigzag printed circuit heat exchanger for supercritical CO2 Brayton cycle. J. Therm. Sci. 2021, 30, 1289–1301. [Google Scholar] [CrossRef]
- Ngo, T.L.; Kato, Y.; Nikitin, K.; Tsuzuki, N. New printed circuit heat exchanger with S-shaped fins for hot water supplier. Exp. Therm. Fluid Sci. 2006, 30, 811–819. [Google Scholar] [CrossRef]
- Ngo, T.L.; Kato, Y.; Nikitin, K.; Ishizuka, T. Heat transfer and pressure drop correlations of microchannel heat exchangers with S-shaped and zigzag fins for carbon dioxide cycles. Exp. Therm. Fluid Sci. 2007, 32, 560–570. [Google Scholar] [CrossRef]
- Pidaparti, S.R.; Anderson, M.H.; Ranjan, D. Experimental investigation of thermal-hydraulic performance of discontinuous fin printed circuit heat exchangers for supercritical CO2 power cycles. Exp. Therm. Fluid Sci. 2019, 106, 119–129. [Google Scholar] [CrossRef]
- Aneesh, A.M.; Sharma, A.; Srivastava, A.; Chaudhury, P. Effects of wavy channel configurations on thermal-hydraulic characteristics of printed circuit heat exchanger (PCHE). Int. J. Heat Mass Transf. 2018, 118, 304–315. [Google Scholar] [CrossRef]
- Xing, K.; Xiao, G.; Xu, H.; Ji, Y. Experimental and numerical investigation on the dynamic characteristics of a lab-scale transcritical CO2 loop. Energy Conv. Manag. 2021, 245, 114384. [Google Scholar] [CrossRef]
- Ji, Y.; Xing, K.; Cen, K.; Ni, M.; Xu, H.; Xiao, G. Numerical study on flow and heat transfer characteristics of trapezoidal printed circuit heat exchanger. Micromachines 2021, 12, 1589. [Google Scholar] [CrossRef]
- Kim, S.G.; Lee, Y.; Ahn, Y.; Lee, J.I. CFD aided approach to design printed circuit heat exchangers for supercritical CO2 Brayton cycle application. Ann. Nucl. Energy 2016, 92, 175–185. [Google Scholar] [CrossRef]












| Parameters | Hot Side | Cold Side |
|---|---|---|
| Inlet temperature, °C | 200–400 | 40–100 |
| Inlet pressure, MPa | 7.50–12 | 8.25–12.75 |
| Mass flow rate, kg/h | 20–60 | 20–60 |
| Reynolds number range | 4800–14,000 | 10,000–30,000 |
| Parameters | Position | Instruments | Manufacturer | Type | Range | Max Error |
|---|---|---|---|---|---|---|
| Mass flow rate | Pump outlet | Coriolis flowmeter | Rheonik | RHM 03 | 0~300 kg/h | 0.20% |
| Temperature | Preheat outlet | PT100 | Sinomeasure | WZP-Pt100 | −50~200 °C | A level |
| Temperature | PCHE cold inlet | K-type thermocouple | Omega | TJ36-CAIN-14U-6-CC-XSIB | 0~1150 °C | 0.75% |
| Temperature | PCHE cold outlet | K-type thermocouple | Omega | TJ36-CAIN-14U-6-CC-XSIB | 0~1150 °C | 0.75% |
| Temperature | PCHE hot inlet | K-type thermocouple | Omega | TJ36-CAIN-14U-6-CC-XSIB | 0~1150 °C | 0.75% |
| Temperature | PCHE hot outlet | K-type thermocouple | Omega | TJ36-CAIN-14U-6-CC-XSIB | 0~1150 °C | 0.75% |
| Pressure loss | PCHE cold side | Differential pressure sensor | CEOPA | CPS843M | 0~500 kPa | 0.10% |
| Pressure loss | PCHE hot side | Differential pressure sensor | CEOPA | CPS843M | 0~500 kPa | 0.10% |
| Parameters | U | Nu | Re | Heat Recovery Efficiency | Pressure Drop |
|---|---|---|---|---|---|
| The maximum relative uncertainty | 5.06% | 6.34% | 4.86% | 5.24% | 0.14% |
| Mass Flow Rate, kg/h | Pressure, MPa | Inlet Temperature, °C | |
|---|---|---|---|
| Hot side | 40 | 8 | 200–400 |
| Cold side | 40 | 9 | 40–100 |
| Number of Grids, ×104 | Outlet Temperature, °C | Pressure Drop, kPa | ||
|---|---|---|---|---|
| Cold Side | Hot Side | Cold Side | Hot Side | |
| 61 | 132.98 | 120.75 | 6.61 | 2.31 |
| 164 | 133.83 | 120.01 | 6.47 | 2.23 |
| 224 | 134.31 | 119.55 | 6.35 | 2.20 |
| 347 | 134.42 | 119.51 | 6.34 | 2.18 |
| 445 | 134.51 | 119.48 | 6.33 | 2.18 |
| Mass Flow Rate, kg/h | Cold Average Reynolds Number | Hot Average Reynolds Number |
|---|---|---|
| 7.50 | 3796 | 1821 |
| 10 | 5070 | 2424 |
| 12.50 | 6346 | 3026 |
| 15 | 7622 | 3628 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, Y.; Wang, Z.; Wang, M.; Liu, Y.; Xu, H.; Zhu, P.; Ma, S.; Yang, Z.; Xiao, G. Experimental and Numerical Study on Thermal Hydraulic Performance of Trapezoidal Printed Circuit Heat Exchanger for Supercritical CO2 Brayton Cycle. Energies 2022, 15, 4940. https://doi.org/10.3390/en15144940
Ji Y, Wang Z, Wang M, Liu Y, Xu H, Zhu P, Ma S, Yang Z, Xiao G. Experimental and Numerical Study on Thermal Hydraulic Performance of Trapezoidal Printed Circuit Heat Exchanger for Supercritical CO2 Brayton Cycle. Energies. 2022; 15(14):4940. https://doi.org/10.3390/en15144940
Chicago/Turabian StyleJi, Yuxuan, Zheng Wang, Mingxuan Wang, Yafei Liu, Haoran Xu, Peiwang Zhu, Shilei Ma, Zhigang Yang, and Gang Xiao. 2022. "Experimental and Numerical Study on Thermal Hydraulic Performance of Trapezoidal Printed Circuit Heat Exchanger for Supercritical CO2 Brayton Cycle" Energies 15, no. 14: 4940. https://doi.org/10.3390/en15144940
APA StyleJi, Y., Wang, Z., Wang, M., Liu, Y., Xu, H., Zhu, P., Ma, S., Yang, Z., & Xiao, G. (2022). Experimental and Numerical Study on Thermal Hydraulic Performance of Trapezoidal Printed Circuit Heat Exchanger for Supercritical CO2 Brayton Cycle. Energies, 15(14), 4940. https://doi.org/10.3390/en15144940