Optimization of a Solar Water Pumping System in Varying Weather Conditions by a New Hybrid Method Based on Fuzzy Logic and Incremental Conductance
Abstract
:1. Introduction
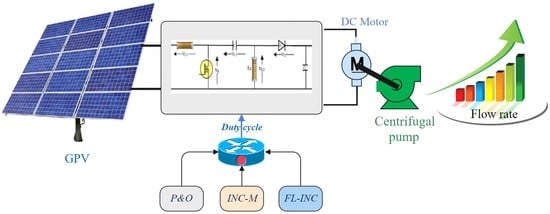
2. Description of the Solar Water Pumping System
3. Solar Pumping System Constitutions
3.1. PV Generator
3.2. Pump Centrifuge
- ▪
- Torque (Cr)—speed (ω):
- ▪
- Flow (Q)—speed (ω):
- ▪
- Height (H)—speed (ω):
3.3. Matching Stage: SEPIC Converter
4. Solar Water Pumping System Optimization Techniques
4.1. P&O Optimization Technique
- ▪
- At a fixed voltage V(k), the corresponding power P(k) delivered by the generator is measured;
- ▪
- After a certain delay, the algorithm imposes a voltage V(k + 1) = V(k) + ΔV and also measures the corresponding power P(k + 1);
- ▪
- If P(k + 1) is greater than P(k), the algorithm seeks to apply for a higher-voltage V(k + 1) = V(k) + ΔV;
- ▪
- Otherwise, the algorithm instead looks to decrease the voltage V(k) = V(k + 1) − ΔV.
4.2. Incremental Conductance Modified (M-INC) Optimization Technique
4.3. FL-INC Hybrid Optimization Technique
- ▪
- If the conductance value is very big, the variation of the duty cycle (δα) must be big so as to quickly bring this conductance to zero;
- ▪
- If the conductance value is close to zero, slight variations in the duty cycle should be applied;
- ▪
- If the conductance value is close to zero and approaches it quickly, the duty cycle must be constant to avoid strong overshoot;
- ▪
- If the conductance reaches zero and the output voltage is not stable, the duty cycle should be varied a little to reduce fluctuations;
- ▪
- If the conductance reaches zero and the output voltage of the converter is stable, the duty cycle should be kept constant;
- ▪
- If the value of the conductance variation is greater than zero, the variation of the duty cycle is negative and vice versa.
5. Simulation Results of the Solar Water Pumping System
5.1. Simulation Conditions
- ▪
- Constant irradiance in the intervals: (0, t1), (t2, t3), (t3, t4), (t4, t5), (t6, t7), and (t8, t9);
- ▪
- Variable irradiance in the intervals: (t1, t2) and (t7, t8);
- ▪
- Abrupt changes in irradiance at times t3 and t4;
5.2. Simulation Results of the Direct Coupling
5.3. Simulation Results Using the P&O Optimization Algorithm
5.4. Simulation Results Using the M-INC Optimization Algorithm
5.5. Simulation Results Using the FL-INC Optimization Algorithm
6. Comparative Study between the Studied Optimization Techniques
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SWPS | solar water pumping system |
| FL-INC | fuzzy logic and incremental conductance |
| SEPIC | single-ended primary inductance converter |
| INC | incremental conductance |
| M-INC | modified incremental conductance |
| P&O | perturb and observe |
| HC | hill climbing |
| ABC | artificial bee colony |
| PV | photovoltaic |
| IGBT | insulated gate bipolar transistor |
| MOSFET | metal oxide semiconductor field effect transistor |
| GPV | generator photovoltaic |
| MPP | maximum power point |
| MPPT | maximum power point tracking |
References
- Al-Sumaiti, A.S.; Ahmed, M.H.; Salama, M. Residential Load Management Under Stochastic Weather Condition in Developing Countries. Electr. Power Compon. Syst. 2014, 42, 1452–1473. [Google Scholar] [CrossRef]
- Mossa, M.A.; Gam, O.; Bianchi, N.; Quynh, N.V. Enhanced Control and Power Management for a Renewable Energy-Based Water Pumping System. IEEE Access 2022, 10, 36028–36056. [Google Scholar] [CrossRef]
- Mossa, M.A.; Gam, O.; Bianchi, N. Dynamic Performance Enhancement of a Renewable Energy System for Grid Connection and Stand-Alone Operation with Battery Storage. Energies 2022, 15, 1002. [Google Scholar] [CrossRef]
- Mossa, M.A.; Echeikh, H.; Quynh, N.V.; Bianchi, N. Performance dynamics improvement of a hybrid wind/fuel cell/battery system for standalone operation. IET Renew. Power Gener. 2022, 1–27. [Google Scholar] [CrossRef]
- Banhidarah, A.K.; Al-Sumaiti, A.S. Heuristic search algorithms for optimal locations and sizing of distributed generators in the grid: A brief recent review. In Proceedings of the 2018 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, Sharjah, Abu Dhabi, United Arab Emirates, 6 February–5 April 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Sharma, G.D.; Shah, M.I.; Shahzad, U.; Jain, M.; Chopra, R. Exploring the nexus between agriculture and greenhouse gas emissions in BIMSTEC region: The role of renewable energy and human capital as moderators. J. Environ. Manag. 2021, 297, 113316. [Google Scholar] [CrossRef]
- Mossa, M.A.; Echeikh, H.; Iqbal, A. Enhanced control technique for a sensor-less wind driven doubly fed induction generator for energy conversion purpose. Energy Rep. 2021, 7, 5815–5833. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Z. Exploring the impact of media discourse on social perceptions towards biomass energy utilization in China. Energy Strategy Rev. 2022, 42, 100896. [Google Scholar] [CrossRef]
- Li, J.; Yang, Z.; Yu, Z.; Shen, J.; Duan, Y. Influences of climatic environment on the geothermal power generation potential. Energy Convers. Manag. 2022, 268, 115980. [Google Scholar] [CrossRef]
- Fujiwara, R.; Fukuhara, R.; Ebiko, T.; Miyatake, M. Forecasting design values of tidal/ocean power generator in the strait with unidirectional flow by deep learning. Intell. Syst. Appl. 2022, 14, 200067. [Google Scholar] [CrossRef]
- World Health Organization. Progress on Sanitation and Drinking Water: 2015 Update and MDG Assessment; World Health Organization: Geneva, Switzerland, 2015. [Google Scholar]
- Al-Sumaiti, A.S.; Kavousi-Fard, A.; Salama, M.; Pourbehzadi, M.; Reddy, S.; Rasheed, M.B. Economic Assessment of Distributed Generation Technologies: A Feasibility Study and Comparison with the Literature. Energies 2020, 13, 2764. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Sultan, H.M.; Do, T.D.; Kamel, O.M.; Mossa, M.A. Coyote Optimization Algorithm for Parameters Estimation of Various Models of Solar Cells and PV Modules. IEEE Access 2020, 8, 111102–111140. [Google Scholar] [CrossRef]
- Belhaouas, N.; Mehareb, F.; Assem, H.; Kouadri-Boudjelthia, E.; Bensalem, S.; Hadjrioua, F.; Aissaoui, A.; Bakria, K. A new approach of PV system structure to enhance performance of PV generator under partial shading effect. J. Clean. Prod. 2021, 317, 128349. [Google Scholar] [CrossRef]
- Hilali, A.; Mardoude, Y.; Mahfoud, M.E.; Essahlaoui, A.; Houssam, M.; Rahali, A. Photovoltaic Water Pumping System: Modeling and Simulation of Characteristics for Direct Coupling. In Digital Technologies and Applications; Springer: Cham, Switzerland, 2022; pp. 651–660. [Google Scholar] [CrossRef]
- Spier, D.W.; Oggier, G.G.; da Silva, S.A.O. Dynamic modeling and analysis of the bidirectional DC-DC boost-buck converter for renewable energy applications. Sustain. Energy Technol. Assess. 2019, 34, 133–145. [Google Scholar] [CrossRef]
- Sakthivel, K.; Krishnasamy, R.; Balasubramanian, K.; Krishnakumar, V.; Ganesan, M. Averaged state space modeling and the applicability of the series Compensated Buck-Boost converter for harvesting solar Photo Voltaic energy. Sustain. Energy Technol. Assess. 2022, 53, 102611. [Google Scholar] [CrossRef]
- Hilali, A.; Mardoude, Y.; Akka, Y.B.; Alami, H.E.; Rahali, A. Design, modeling and simulation of perturb and observe maximum power point tracking for a photovoltaic water pumping system. Int. J. Electr. Comput. Eng. IJECE 2022, 12, 4. [Google Scholar] [CrossRef]
- Jately, V.; Azzopardi, B.; Joshi, J.; Venkateswaran, V.B.; Sharma, A.; Arora, S. Experimental Analysis of hill-climbing MPPT algorithms under low irradiance levels. Renew. Sustain. Energy Rev. 2021, 150, 111467. [Google Scholar] [CrossRef]
- Kumar, R.; Khandelwal, S.; Upadhyay, P.; Pulipaka, S. Global maximum power point tracking using variable sampling time and p-v curve region shifting technique along with incremental conductance for partially shaded photovoltaic systems. Sol. Energy 2019, 189, 151–178. [Google Scholar] [CrossRef]
- Pilakkat, D.; Kanthalakshmi, S. Single phase PV system operating under Partially Shaded Conditions with ABC-PO as MPPT algorithm for grid connected applications. Energy Rep. 2020, 6, 1910–1921. [Google Scholar] [CrossRef]
- Hilali, A.; Mardoude, Y.; Essahlaoui, A.; Rahali, A.; Ouanjli, N.E. Migration to solar water pump system: Environmental and economic benefits and their optimization using genetic algorithm Based MPPT. Energy Rep. 2022, 8, 10144–10153. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Mohamed, M.A.; Al-Sumaiti, A.; Sultan, H.; Mossa, M. A Novel Hybrid Optimization Algorithm for Maximum Power Point Tracking of Partially Shaded Photovoltaic Systems. In Advanced Technologies for Solar Photovoltaics Energy Systems; Motahhir, S., Eltamaly, A.M., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2021; pp. 201–230. [Google Scholar] [CrossRef]
- Eltamaly, A.M. Musical chairs algorithm for parameters estimation of PV cells. Sol. Energy 2022, 241, 601–620. [Google Scholar] [CrossRef]
- Wang, C.; Shi, W.; Wang, X.; Jiang, X.; Yang, Y.; Li, W.; Zhou, L. Optimal design of multistage centrifugal pump based on the combined energy loss model and computational fluid dynamics. Appl. Energy 2017, 187, 10–26. [Google Scholar] [CrossRef]
- Fatigati, F.; di Battista, D.; Cipollone, R. Design improvement of volumetric pump for engine cooling in the transportation sector. Energy 2021, 231, 120936. [Google Scholar] [CrossRef]
- Yao, F.; Sun, H. The stability criterion of pumps. In Proceedings of the 2011 International Conference on Electronic Mechanical Engineering and Information Technology, Harbin, China, 12–14 August 2011; pp. 342–344. [Google Scholar] [CrossRef]
- Rais, Y.; Aroudi, A.E.; Zakriti, A.; Khamlichi, A. Modeling and design of voltage-mode controlled PV-fed SEPIC converter. IFAC-Pap. 2022, 55, 514–519. [Google Scholar] [CrossRef]
- Chellakhi, A.; el Beid, S.; Abouelmahjou, Y. An improved adaptable step-size P&O MPPT approach for standalone photovoltaic systems with battery station. Simul. Model. Pract. Theory 2022, 121, 102655. [Google Scholar] [CrossRef]
- Mossa, M.A.; Gam, O.; Bianchi, N. Performance Enhancement of a Hybrid Renewable Energy System Accompanied with Energy Storage Unit Using Effective Control System. Int. J. Robot. Control Syst. 2022, 2, 140–171. [Google Scholar] [CrossRef]
- Tey, K.S.; Mekhilef, S. Modified incremental conductance MPPT algorithm to mitigate inaccurate responses under fast-changing solar irradiation level. Sol. Energy 2014, 101, 333–342. [Google Scholar] [CrossRef]
- Motahhir, S.; Chalh, A.; el Ghzizal, A.; Derouich, A. Development of a low-cost PV system using an improved INC algorithm and a PV panel Proteus model. J. Clean. Prod. 2018, 204, 355–365. [Google Scholar] [CrossRef]
- Ganjeh-Alamdari, M.; Alikhani, R.; Perfilieva, I. Fuzzy logic approach in salt and pepper noise. Comput. Electr. Eng. 2022, 102, 108264. [Google Scholar] [CrossRef]
- Reyes-García, C.A.; Torres-García, A.A. Chapter 8—Fuzzy logic and fuzzy systems. In Biosignal Processing and Classification Using Computational Learning and Intelligence; Torres-García, A.A., Reyes-García, C.A., Villaseñor-Pineda, L., Mendoza-Montoya, O., Eds.; Academic Press: Cambridge, MA, USA, 2022; pp. 153–176. [Google Scholar] [CrossRef]
- Bose, B.K. Chapter 11—Fuzzy logic and applications. In Power Electronics and Motor Drives, 2nd ed.; Bose, B.K., Ed.; Academic Press: Cambridge, MA, USA, 2021; pp. 789–874. [Google Scholar] [CrossRef]




















| Voc (V) | Isc (A) | Pmpp (W) | Rsh (kΩ) | Rs (mΩ) | Vmpp (V) | Impp (A) |
|---|---|---|---|---|---|---|
| 41 | 10.3 | 330 | 1 | 73 | 34.6 | 9.55 |
| Irradiance (W·m−2) | GPV Temperature (°C) | Peak Power (W·m−2) |
|---|---|---|
| 800 | 25 | 1347 |
| 900 | 25 | 1508 |
| 1000 | 25 | 1657 |
| 1100 | 25 | 1803 |
| 1200 | 25 | 1950 |
| 1250 | 25 | 2018 |
| Component | Designate | Value |
|---|---|---|
| Coupling capacitor | C1 | 250 µF |
| Inductor | L1 = L2 | 1.5 mH |
| Filtering capacitor | C2 | 500 µF |
| Hashing frequency | f | 10 kHz |
| ΔE | NB | NS | Z | PS | PB | |
|---|---|---|---|---|---|---|
| E | ||||||
| NB | Z | Z | PB | PB | PB | |
| NS | Z | Z | PS | PS | PS | |
| Z | PS | Z | Z | Z | NS | |
| PS | NS | NS | NS | Z | Z | |
| PB | NB | NB | NB | Z | Z | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hilali, A.; El Ouanjli, N.; Mahfoud, S.; Al-Sumaiti, A.S.; Mossa, M.A. Optimization of a Solar Water Pumping System in Varying Weather Conditions by a New Hybrid Method Based on Fuzzy Logic and Incremental Conductance. Energies 2022, 15, 8518. https://doi.org/10.3390/en15228518
Hilali A, El Ouanjli N, Mahfoud S, Al-Sumaiti AS, Mossa MA. Optimization of a Solar Water Pumping System in Varying Weather Conditions by a New Hybrid Method Based on Fuzzy Logic and Incremental Conductance. Energies. 2022; 15(22):8518. https://doi.org/10.3390/en15228518
Chicago/Turabian StyleHilali, Abdelilah, Najib El Ouanjli, Said Mahfoud, Ameena Saad Al-Sumaiti, and Mahmoud A. Mossa. 2022. "Optimization of a Solar Water Pumping System in Varying Weather Conditions by a New Hybrid Method Based on Fuzzy Logic and Incremental Conductance" Energies 15, no. 22: 8518. https://doi.org/10.3390/en15228518
APA StyleHilali, A., El Ouanjli, N., Mahfoud, S., Al-Sumaiti, A. S., & Mossa, M. A. (2022). Optimization of a Solar Water Pumping System in Varying Weather Conditions by a New Hybrid Method Based on Fuzzy Logic and Incremental Conductance. Energies, 15(22), 8518. https://doi.org/10.3390/en15228518