Accurate State of Charge Estimation for Real-World Battery Systems Using a Novel Grid Search and Cross Validated Optimised LSTM Neural Network
Abstract
:1. Introduction
1.1. Literature Review
- (1)
- Large sampling interval and low data accuracy for real-world EV data.
- (2)
- Model-based approaches rely on complex mathematical models and have limited estimation accuracy.
- (3)
- Most machine learning-based SOC estimation methods rely on large amounts of offline data and are still in the laboratory stage.
1.2. Contributions of this Work
- (1)
- The EV operating conditions are divided into parking charging, travel charging, and finish charging. The relevant parameters are extracted under each operating condition for SOC estimation using Pearson analysis.
- (2)
- Optimizing LSTM neural network hyperparameters based on grid search and cross validation to improve the accuracy of the proposed method and the absolute error of SOC estimation within 4% for real-world EVs.
- (3)
- The method’s accuracy is verified by using Gaussian noise to expand the data for working conditions with small data, and the robustness of the method was verified by operating data of different EVs.
1.3. Organization of the Paper
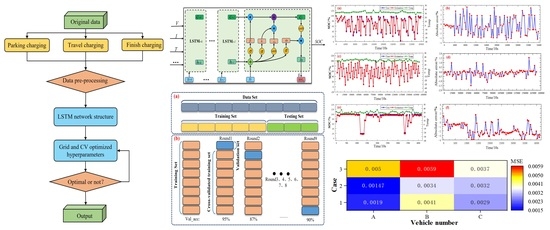
2. Data Description and Pre-Processing
2.1. Data Description
2.2. Data Preprocessing
3. Methodology
3.1. Battery SOC Definition
3.2. Pearson Related Analysis
3.3. LSTM Neural Networks
3.4. Grid Search and Cross Validation Optimation
3.5. Gaussian Noise
4. Results and Discussion
4.1. Pearson and Heat Map Analysis of SOC Estimation Related Parameters
4.2. SOC Estimation by LSTM Network Based on GSCV Optimization
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ren, X.; Liu, S.; Yu, X.; Dong, X. A method for state-of-charge estimation of lithium-ion batteries based on PSO-LSTM. Energy 2021, 234, 121236. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Chen, W.; Wang, L.-Y.; Qu, C. Online joint-prediction of multi-forward-step battery SOC using LSTM neural networks and multiple linear regression for real-world electric vehicles. J. Energy Storage 2020, 30, 101459. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Zhang, T.; Yin, H.; Zhang, H.; Huo, W.; Zhang, Y.; Li, Y. Research on integration simulation and balance control of a novel load isolated pure electric driving system. Energy 2019, 189, 116220. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y.; Wu, J.; Cheng, W.; Zhu, Q. SOC estimation for lithium-ion battery using the LSTM-RNN with extended input and constrained output. Energy 2023, 262, 125375. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, S.; Li, W.; Miao, Q. State-of-charge estimation of lithium-ion batteries using LSTM and UKF. Energy 2020, 201, 117664. [Google Scholar] [CrossRef]
- Chen, G.; Jiang, S.; Xie, M.; Yang, F. A hybrid DNN-KF model for real-time SOC estimation of lithium-ion batteries under different ambient temperatures. In Proceedings of the 2022 Global Reliability and Prognostics and Health Management (PHM-Yantai), Yantai, China, 13–16 October 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Xiong, X.; Wang, S.; Fernandez, C.; Yu, C.; Zou, C.; Jiang, C. A novel practical state of charge estimation method: An adaptive improved ampere-hour method based on composite correction factor. Int. J. Energy Res. 2020, 44, 11385–11404. [Google Scholar] [CrossRef]
- Ren, Z.; Du, C.; Wu, Z.; Shao, J.; Deng, W. A comparative study of the influence of different open circuit voltage tests on model-based state of charge estimation for lithium-ion batteries. Int. J. Energy Res. 2021, 45, 13692–13711. [Google Scholar] [CrossRef]
- Bao, Y.; Dong, W.; Wang, D. Online Internal Resistance Measurement Application in Lithium Ion Battery Capacity and State of Charge Estimation. Energies 2018, 11, 1073. [Google Scholar] [CrossRef] [Green Version]
- Cui, Z.; Wang, L.; Li, Q.; Wang, K. A comprehensive review on the state of charge estimation for lithium-ion battery based on neural network. Int. J. Energy Res. 2021, 46, 5423–5440. [Google Scholar] [CrossRef]
- Xie, F.; Wang, S.; Xie, Y.; Fernandezb, C.; Li, X.; Zou, C. A novel battery state of charge estimation based on the joint unscented kalman filter and support vector machine algorithms. Int. J. Electrochem. Sci. 2020, 15, 7935–7953. [Google Scholar] [CrossRef]
- Tian, J.; Xiong, R.; Shen, W.; Lu, J. State-of-charge estimation of LiFePO4 batteries in electric vehicles: A deep-learning enabled approach. Appl. Energy 2021, 291, 116812. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, J.; Gao, T.; Ren, S. State of Charge Estimation of Li-Ion Battery Based on Adaptive Sliding Mode Observer. Sensors 2022, 22, 7678. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Tang, Y.; Ren, J.; Wei, Y. State of charge estimation with the adaptive unscented Kalman filter based on an accurate equivalent circuit model. J. Energy Storage 2021, 41, 102840. [Google Scholar] [CrossRef]
- Kwak, M.; Lkhagvasuren, B.; Park, J.; You, J.-H. Parameter Identification and SOC Estimation of a Battery Under the Hysteresis Effect. IEEE Trans. Ind. Electron. 2019, 67, 9758–9767. [Google Scholar] [CrossRef]
- Snoussi, J.; Ben Elghali, S.; Zerrougui, M.; Bensoam, M.; Benbouzid, M.; Mimouni, M.F. Unknown input observer design for lithium-ion batteries SOC estimation based on a differential-algebraic model. J. Energy Storage 2020, 32, 101973. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, S.; Jing, B.; Yang, C.; Ji, J.; Zhao, Z. Fractional variable-order calculus based state of charge estimation of Li-ion battery using dual fractional order Kalman filter. J. Energy Storage 2022, 52, 104685. [Google Scholar] [CrossRef]
- Li, R.; Wang, H.; Dai, H.; Hong, J.; Tong, G.; Chen, X. Accurate state of charge prediction for real-world battery systems using a novel dual-dropout-based neural network. Energy 2022, 250, 123853. [Google Scholar] [CrossRef]
- Peng, L.; Wang, L.; Xia, D.; Gao, Q. Effective energy consumption forecasting using empirical wavelet transform and long short-term memory. Energy 2021, 238, 121756. [Google Scholar] [CrossRef]
- Azhar, I.F.; Putranto, L.M.; Irnawan, R. Development of PMU-Based Transient Stability Detection Methods Using CNN-LSTM Considering Time Series Data Measurement. Energies 2022, 15, 8241. [Google Scholar] [CrossRef]
- Lim, S.-C.; Huh, J.-H.; Hong, S.-H.; Park, C.-Y.; Kim, J.-C. Solar Power Forecasting Using CNN-LSTM Hybrid Model. Energies 2022, 15, 8233. [Google Scholar] [CrossRef]
- Peng, L.; Liu, S.; Liu, R.; Wang, L. Effective long short-term memory with differential evolution algorithm for electricity price prediction. Energy 2018, 162, 1301–1314. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Yao, Y. Fault prognosis of battery system based on accurate voltage abnormity prognosis using long short-term memory neural networks. Appl. Energy 2019, 251, 113381. [Google Scholar] [CrossRef]
- Fahad, S.; Su, F.; Khan, S.U.; Naeem, M.R.; Wei, K. Implementing a novel deep learning technique for rainfall forecasting via climatic variables: An approach via hierarchical clustering analysis. Sci. Total Environ. 2023, 854, 158760. [Google Scholar] [CrossRef] [PubMed]
- Hong, J.; Wang, Z.; Chen, W.; Yao, Y. Synchronous multi-parameter prediction of battery systems on electric vehicles using long short-term memory networks. Appl. Energy 2019, 254, 113648. [Google Scholar] [CrossRef]
- Song, X.; Yang, F.; Wang, D.; Tsui, K.-L. Combined CNN-LSTM Network for State-of-Charge Estimation of Lithium-Ion Batteries. IEEE Access 2019, 7, 88894–88902. [Google Scholar] [CrossRef]
- Erten, G.E.; Keser, S.B.; Yavuz, M. Grid Search Optimised Artificial Neural Network for Open Stope Stability Prediction. Int. J. Min. Reclam. Environ. 2021, 35, 600–617. [Google Scholar] [CrossRef]
- Shi, Q.; Liu, M.; Hang, L. A novel distribution system state estimator based on robust cubature particle filter used for non-gaussian noise and bad data scenarios. IET Gener. Transm. Distrib. 2021, 16, 1385–1399. [Google Scholar] [CrossRef]
- Wang, Z.; Fotouhi, A.; Auger, D.J. State of Charge Estimation in Lithium-Sulfur Cells Using LSTM Recurrent Neural Networks. In Proceedings of the 2020 European Control Conference (ECC), St. Petersburg, Russia, 12–15 May 2020. [Google Scholar] [CrossRef]
- Wei, M.; Ye, M.; Li, J.B.; Wang, Q.; Xu, X. State of Charge Estimation of Lithium-Ion Batteries Using LSTM and NARX Neural Networks. IEEE Access 2020, 8, 189236–189245. [Google Scholar] [CrossRef]










| r | Correlation |
|---|---|
| 0.8~1 | Extremely strong |
| 0.6~0.8 | Strong |
| 0.4~0.6 | Moderate |
| 0.2~0.4 | Weak |
| 0.0~0.2 | Extremely weak or no |
| Parameters | |||
|---|---|---|---|
| Speed | NAN | −0.0300 | NAN |
| Charging status | NAN | NAN | NAN |
| Total voltage | 0.9673 | 0.9561 | 0.9736 |
| Total Current | 0.5501 | −0.0227 | NAN |
| Mileage | −0.1967 | −0.2587 | −0.1295 |
| Maximum cell voltage | 0.9579 | 0.9657 | 0.9752 |
| Maximum cell voltage number | −0.5286 | −0.1829 | −0.0228 |
| Minimum cell voltage | 0.9661 | 0.9665 | 0.9754 |
| Minimum cell voltage number | −0.268 | −0.2797 | −0.2254 |
| Maximum temperature | −0.1938 | 0.2884 | −0.2567 |
| Maximum temperature probe number | 0.0750 | −0.0685 | 0.0805 |
| Minimum temperature | −0.1549 | 0.2711 | −0.2037 |
| Minimum temperature probe number | −0.1507 | 0.0103 | −0.2108 |
| Insulation resistance | 0.0890 | −0.0501 | −0.0186 |
| DCDC status | 0.0050 | 0.0417 | −0.0356 |
| Single temperature number | NAN | NAN | NAN |
| Single voltage number | NAN | NAN | NAN |
| Gear | NAN | −0.0396 | NAN |
| Condition/Error | Maximum Absolute Error | Minimum Absolute Error | MSE |
|---|---|---|---|
| Parking charging | 3.61 | −3.35 | 0.0042 |
| Travel charging | 1.54 | −1.49 | 0.0031 |
| Finish charging | 1.64 | −3.85 | 0.0067 |
| Method | Battery Chemistry | Estimated Target | Research Environment | Precision |
|---|---|---|---|---|
| PSO-LSTM [1] | Li-ion battery | SOC | Laboratory experiment | MAE < 0.2% RMSE < 0.3% |
| LSTM-RNN [4] | Li-ion battery | SOC | Laboratory experiment | RMSE < 1.5% |
| CNN-LSTM [5] | Li-ion battery | SOC | Laboratory experiment | RMSE < 1% MAE < 1% |
| LSTM [29] | Li-sulfur battery | SOC | Laboratory experiment | RMSE < 6% |
| NARX-LSTM [30] | Li-ion battery | SOC | Laboratory experiment | RMSE < 1% MAE < 1% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, J.; Liang, F.; Gong, X.; Xu, X.; Yu, Q. Accurate State of Charge Estimation for Real-World Battery Systems Using a Novel Grid Search and Cross Validated Optimised LSTM Neural Network. Energies 2022, 15, 9654. https://doi.org/10.3390/en15249654
Hong J, Liang F, Gong X, Xu X, Yu Q. Accurate State of Charge Estimation for Real-World Battery Systems Using a Novel Grid Search and Cross Validated Optimised LSTM Neural Network. Energies. 2022; 15(24):9654. https://doi.org/10.3390/en15249654
Chicago/Turabian StyleHong, Jichao, Fengwei Liang, Xun Gong, Xiaoming Xu, and Quanqing Yu. 2022. "Accurate State of Charge Estimation for Real-World Battery Systems Using a Novel Grid Search and Cross Validated Optimised LSTM Neural Network" Energies 15, no. 24: 9654. https://doi.org/10.3390/en15249654
APA StyleHong, J., Liang, F., Gong, X., Xu, X., & Yu, Q. (2022). Accurate State of Charge Estimation for Real-World Battery Systems Using a Novel Grid Search and Cross Validated Optimised LSTM Neural Network. Energies, 15(24), 9654. https://doi.org/10.3390/en15249654