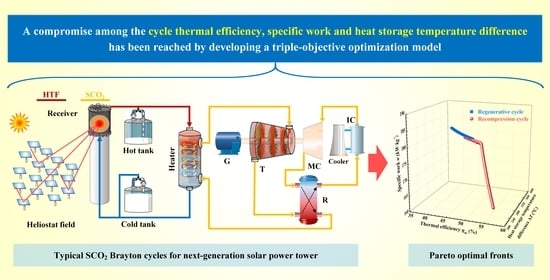
Triple-Objective Optimization of SCO₂ Brayton Cycles for Next-Generation Solar Power Tower

Abstract

In this paper, the SCO₂ Brayton regenerative and recompression cycles are studied and optimized for a next-generation solar power tower under a maximum cycle temperature of over 700 °C. First, a steady-state thermodynamic model is developed and validated, and the impacts of different operating parameters on three critical performance indexes, including the cycle thermal efficiency, specific work, and heat storage temperature difference, are analyzed. The results reveal that these performance indexes are influenced by the operating pressures, the SCO₂ split ratio, and the effectiveness of the regenerators in complex ways. Subsequently, considering the three performance indexes as the optimization objectives, a triple-objective optimization is carried out to determine the optimal operating variables with the aim of obtaining Pareto solutions for both cycles. The optimization indicates that the regenerative cycle can achieve the maximum heat storage temperature difference and the maximum specific work of 396.4 °C and 180.6 kW·kg⁻¹, respectively, while the recompression cycle can reach the maximum thermal efficiency of 55.95%. Moreover, the optimized maximum and minimum pressure values of both cycles are found to be around 30 MPa and 8.2 MPa, respectively. Additionally, the distributions of the optimized values of the regenerator effectiveness and the SCO₂ split ratio show different influences on the performance of the cycles. Therefore, different cycles with different optimized variables should be considered to achieve specific cycle performance. When considering thermal efficiency as the most important performance index, the recompression cycle should be adopted. Meanwhile, its SCO₂ split ratio and the regenerator effectiveness should be close to 0.7 and 0.95, respectively. When considering heat storage temperature difference or specific work as the most important performance index, the regenerative cycle should be adopted. Meanwhile, its regenerator effectiveness should be close to 0.75. The results from this study will be helpful for the optimization of superior SCO₂ cycles for next-generation solar tower plants.

1. Introduction

In recent years, the escalating global consumption of fossil fuels has led to the more pronounced occurrence of environmental pollution and ecological degradation [1,2]. To reduce reliance on traditional fossil fuels and mitigate their negative impacts, renewable energy technologies have experienced rapid advancements [3,4]. Solar thermal power is an important alternative solar power generation technology possessing the ability of heat storage [5,6]. The primary objective of solar thermal power technology development is to enhance thermal efficiency, elevate specific work, and accomplish large-scale heat storage. Among the available solar thermal power technologies, including the solar power tower (SPT) [7,8], solar dish collector [9,10], linear Fresnel reflector [11,12] and parabolic trough collector [13,14,15], the SPT is a promising option that is expected to meet the above development requirements [16].

Currently, commercial SPT plants operate with receiver outlet temperatures below 565 °C and use the steam Rankine cycle as their power cycle [17]. This cycle yields a maximum cycle temperature of around 550 °C and a thermal efficiency of no more than 44% [18]. To increase the economic competitiveness of these plants, it is essential to increase their thermal efficiency by elevating their maximum cycle temperature [19] and developing a more advanced power cycle [20]. Recent studies have shown that next-generation SPT plants could achieve maximum cycle temperatures exceeding 700 °C [18,21]. Additionally, at a maximum cycle temperature of above 600 °C, the supercritical carbon dioxide (SCO₂) Brayton cycle has the potential to outperform the steam Rankine cycle in terms of thermal efficiency [22,23]. Meanwhile, Chen et al. [24] found that the SCO₂ Brayton cycle can produce a larger net work output than the steam Rankine cycle at a maximum cycle temperature of 620 °C, making it more competitive. These two performance advantages become more significant as the maximum cycle temperature increases [25]. Moreover, the SCO₂ cycle’s heater can achieve a temperature difference exceeding 200 °C between its two terminals [26], making it highly compatible with the heat storage unit [27]. Furthermore, employing the SCO₂ cycle in an SPT grants several advantages over the steam Rankine cycle, including greater adaptability to off-design operating conditions [28], applicability to arid areas using dry-cooling methods [29], and a smaller heat exchanger and turbomachinery [30]. In summary, the SCO₂ Brayton cycle has shown great potential to integrate with next-generation SPT plants.

In an SPT plant, improving the thermal efficiency, specific work, and compatibility with the heat storage unit has always been a critical aspect of the SCO₂ Brayton cycle. Consequently, numerous studies have recently been conducted to optimize the performance of various SCO₂ cycle layouts in SPT systems. Many of these studies have advocated for regenerative and recompression cycles due to their simplicity, compactness, and favorable cycle performance [31]. For instance, Wang et al. [28] and Guo et al. [32] optimized several SCO₂ Brayton cycle layouts incorporated in the SPT plant and compared the optimization results. Their results indicated that the recompression cycle could offer relatively high thermal efficiency with a relatively simple layout, while the regenerative cycle could provide relatively high specific work and heat storage temperature difference with the simplest layout. Fahad et al. [33] integrated and optimized five SCO₂ Brayton cycles within an SPT system, comparing their net work outputs and thermal efficiencies at different time points. Their results indicated that the regenerative and recompression cycles could achieve the best performance at different time. Similarly, Chen et al. [34] evaluated six SCO₂ Brayton cycles in a next-generation SPT system and optimized each cycle based on thermal efficiency and specific work under varying temperatures. They concluded that the recompression and regenerative cycles were the most suitable options for the next-generation SPT system. Wang et al. [35] further optimized the recompression cycle to enhance the SPT system’s exergy efficiency. Their findings highlighted the importance of increasing the system’s operating temperature to improve the recompression and overall system performance. However, most optimization studies on SCO₂ Brayton cycles have mainly focused on single-objective or dual-objective optimizations, aiming to improve thermal efficiency, specific work, or compatibility with the heat storage unit. Few studies have explored the triple-objective optimization of the three critical performance indexes.

In this paper, parameter analysis and the triple-objective optimization of the regenerative and recompression cycles are conducted for a next-generation SPT system wherein a typical maximum cycle temperature of 750 °C is considered. Initially, the impacts of changes in operating pressure, regenerator effectiveness, and the SCO₂ split ratio on thermal efficiency, specific work (which denotes the net work output), and the heat storage temperature difference (which denotes the ability to pair with the heat storage unit) are investigated. Subsequently, a triple-objective optimization for each SCO₂ cycle is conducted, and the optimization results are compared and discussed. Finally, the relationships between the optimized variables and the three optimization objectives are further analyzed.

In a typical next-generation solar power tower plant operating at above 700 °C, the operational processes follow a defined sequence, as illustrated in Figure 1 and Figure 2. Firstly, a heliostat field is employed to reflect the incident solar radiation to a receiver located at the top of a central tower. Then, a molten chloride salt [36] that can operate at above 700 °C is used as the heat transfer fluid (HTF) to flow into the receiver, where it undergoes heating, resulting in a high-temperature state that is denoted as A in Figure 1 and Figure 2. Subsequently, the high-temperature molten chloride salt at state A bifurcates into two streams. One of the streams flows into the heater to heat the SCO₂ and is subsequently cooled to state B. The other stream is reserved in the hot tank of the heat storage unit. Eventually, the SCO₂ propels the power cycle after undergoing heating in the heater, and the cold HTF at state B is returned to the receiver or stored in the cold tank of the heat storage unit.

The SPT plant utilizing a typical SCO₂ regenerative cycle is delineated in Figure 1a, while the correlation between entropy and temperature (s-T) at each point in this cycle is illustrated in Figure 1b. During the operation of the SCO₂ regenerative cycle, the process commences with the heating of SCO₂ to its maximum pressure and temperature state, denoted as state 1, at the heater outlet. The heated SCO₂ then enters the turbine to expand and is subsequently discharged when it attains its minimum pressure state, which is referred to as state 2. The SCO₂ then undergoes a regeneration process in the regenerator (R) and a cooling process in the dry-cooling inter-cooler (IC) in succession, reaching state 3 and its minimum-temperature state 4, respectively. Then, in order to transition the SCO₂ from state 4 to the maximum-pressure state 5, the main compressor (MC) is operated. The SCO₂ then undergoes another regeneration process in the regenerator (R), improving its temperature to state 6. Eventually, the SCO₂ returns to the heater to complete a cycle process.

An SPT plant utilizing a typical SCO₂ recompression cycle is delineated in Figure 2a along with an illustration of the correlation between entropy and temperature (s-T) in the cycle (see Figure 2b). In contrast to the SCO₂ regenerative cycle, the SCO₂ recompression cycle substitutes the regenerator (R) with a high temperature regenerator (HTR) and a low temperature regenerator (LTR), while also including a re-compressor (RC). The cycle begins with the SCO₂ being heated by the heater and expanding from state 1 to state 2 in the turbine. Then, the SCO₂ at the turbine outlet (state 2) enters the HTR and LTR successively, ultimately arriving at states 3 and 4, respectively. The SCO₂ subsequently splits into two streams, with stream 4a undergoing a cooling process in the dry-cooling inter-cooler (IC) to achieve the minimum temperature state 5 and stream 4b progressing directly to reach the maximum pressure state 8 via the compression process in the re-compressor (RC). Following this, the SCO₂ at the minimum pressure state 5 reaches the maximum-pressure state 6, and state 7, through the main compressor (MC)’s compression process and the LTR’s regeneration process, respectively. Finally, the two streams at states 7 and 8 converge and participate in the HTR’s regeneration process, ultimately arriving at state 10.

2. Methods

In this section, an optimization model combining a steady-state thermodynamic model and a multi-objective genetic algorithm is developed for the SCO₂ Brayton cycle. This model can not only predict the cycle performance reliably but also optimize the cycle by considering three critical performance indexes as its objectives. The details of the thermodynamic model and the multi-objective genetic algorithm are provided as follows.

2.1. Thermodynamic Simulation Model

As the main objective of this work is to examine and improve the performance of the two studied SCO₂ Brayton cycles, for the sake of simplicity, precise simulations of the heliostat field, receiver, and heat storage unit were ignored in our simulation. However, comprehensive steady-state thermodynamic simulation models were meticulously constructed to assess the performance of the two cycles. During the simulation, the thermodynamic variables related to SCO₂ at different temperatures and pressures were obtained by using REFPROP [37]. In addition, the following plausible assumptions were implemented to streamline the simulation procedures:

(1)

The cycles always maintained stable operation [38].

(2)

The potential energy and kinetic energy of each cycle was maintained unaltered [39].

(3)

Heat dissipations and pressure reductions in the cycle were insignificant [40].

(4)

The effectiveness model was suitable while modeling the regenerator [41].

(5)

The cycle performance was not influenced by the mass flow rate of SCO₂ [42].

The fundamental settings utilized in the thermodynamic simulation of the two SCO₂ cycles are presented in

Table 1. Fundamental settings utilized in the thermodynamic simulation.

Parameters	Values
Ambient pressure, p0	101.325 kPa
Ambient temperature, T0	15 °C [19]
HTF high temperature, TA	760 °C [43,44]
Maximum cycle temperature, T1	750 °C
Turbine isentropic efficiency, ηT	93% [45]
Cycle minimum temperature, t4 for regenerative cycle, t5 for recompression cycle	35 °C [19]
Compressor isentropic efficiency, ηMC, ηRC	89% [35]
Mass flow rate of the SCO2, $m_{{\mathrm{SCO}}_2}$	1 kg·s−1 [42]

, while Section 3.1.1 outlines the elaborate simulation procedures for both cycles.

2.1.1. Modeling of the Two SCO₂ Brayton Cycles

After assuming the operating conditions and the fundamental settings of the two SCO₂ cycles, the detailed modeling processes for the cycles are introduced as follows.

For the SCO₂ regenerative cycle, the work contributed by the expansion of the SCO₂ in the turbine (W_T) is firstly determined using Equation (1). Next, the work spent by the compression process of the main compressor (W_MC) is expressed by Equation (2). Hence, the net work output (W_net) generated by the SCO₂ regenerative cycle thus allows for being determined via Equation (3).

$$W_{\mathrm{T}}=m_{{\mathrm{SCO}}_2}\cdot \left(h_1-h_2\right)=m_{{\mathrm{SCO}}_2}\cdot \left(h_1-h_{2\mathrm{S}}\right)\cdot {\eta }_{\mathrm{T}}$$

(1)

$$W_{\mathrm{MC}}=m_{{\mathrm{SCO}}_2}\cdot \left(h_5-h_4\right)=m_{{\mathrm{SCO}}_2}\cdot \left(h_{5\mathrm{S}}-h_4\right)/{\eta }_{\mathrm{MC}}$$

(2)

$$W_{\mathrm{net}}=W_{\mathrm{T}}-W_{\mathrm{MC}}$$

(3)

Here, h_i indicates the SCO₂’s specific enthalpy at each state i; the subscript “s” represents the SCO₂ under ideal conditions.

For the regenerator, the definition equations of its effectiveness, Equations (4) and (5) [35,41], are utilized to derive the thermodynamic variables of the SCO₂ at its outlets and inlets. In this way, h₆ is derived, and the heat obtained by the SCO₂ from the heater (Q) is then determined using Equation (6).

$${\epsilon }_{\mathrm{R}}=\left\{\begin{array}{l}\left(h_2-h_3\right)/\left(h_2-h_{p3,T5}\right) \mathrm{when} T_2-T_3\ge T_6-T_5\\ \left(h_6-h_5\right)/\left(h_{p6,T2}-h_5\right) \mathrm{when} T_2-T_3<T_6-T_5\end{array}\right.$$

(4)

$$h_6-h_5=h_2-h_3$$

(5)

$$Q=m_{{\mathrm{SCO}}_2}\cdot \left(h_1-h_6\right)$$

(6)

Here, h_p3,T5 is the specific enthalpy predicted by selecting the pressure of SCO₂ at state 3 and the temperature of SCO₂ at state 5; h_p6,T2 is the specific enthalpy predicted by selecting the pressure of SCO₂ at state 6 and the temperature of SCO₂ at state 2.

For calculating the minimum temperature of the HTF (T_B), as indicated in Equation (7), it is reasonable to assume that the entropy generations at the heater’s two terminals are equivalent [46]. As a result, Equation (8) can be derived to determine the minimum HTF temperature (T_B) at the heater outlet.

$$\Delta Q/T_1-\Delta Q/T_{\mathrm{A}}=\Delta Q/T_6-\Delta Q/T_{\mathrm{B}}$$

(7)

$$T_B=\frac{T_1\cdot T_6\cdot T_{\mathrm{A}}}{T_1\cdot T_{\mathrm{A}}-T_6\cdot \left(T_{\mathrm{A}}-T_1\right)}$$

(8)

Here, T_A represents the maximum HTF temperature of the heater; ΔQ represents the heat power that is exchanged by the fluids between the two sides of the heater.

The procedures employed to simulate the SCO₂ recompression cycle bear similarities to those employed in the SCO₂ regenerative cycle. This similarity is supported by the presence of energy equilibrium equations, as shown in

Table 2. Energy equilibrium equations for the SCO₂ recompression cycle.

Process or Component	Energy Equilibrium Equations
Turbine	WT = $m_{{\mathrm{SCO}}_2}$·(h1 − h2) = $m_{{\mathrm{SCO}}_2}$·(h1 − h2S)·ηT
Main compressor	WMC = SR·$m_{{\mathrm{SCO}}_2}$·(h6 − h5) = SR·$m_{{\mathrm{SCO}}_2}$·(h6S − h5)/ηMC
Re-compressor	WRC = (1 − SR)·$m_{{\mathrm{SCO}}_2}$·(h8 − h4) = (1 − SR)·$m_{{\mathrm{SCO}}_2}$·(h8S − h4)/ηRC
LTR	ɛLTR= (h3 − h4)/(h3 − hp4,T6) when T3 − T4 ≥ T7 − T6 ɛLTR = (h7 − h6)/(hp7, T3 − h6) when T3 − T4 < T7 − T6 h3 − h4 = SR·(h7 − h6)
HTR	ɛHTR= (h2 − h3)/(h2 − hp3,T9) when T2 − T3 ≥ T10 − Tt9 ɛHTR = (h10 − h9)/(hp10,T2 − h9) when T2 − T3 < T10 − T09 h2 − h3 = h10 − h9
SCO2 merging	h9 =SR·h7 + (1 − SR)·h8
Heater	Q =$m_{{\mathrm{SCO}}_2}$·(h1 − h10) TB = (T1·T10·TA)/[T1·TA − T10·(TA − T1)]
Net work	Wnet = WT − WMC − WRC

. For the sake of brevity, detailed explanations of these equations have been omitted.

2.1.2. Model Validation

To validate the present model, an SCO₂ recompression cycle previously studied by Turchi et al. [47] is simulated using the present model. The specific input variables in

Table 3. Input variables for the validation [47].

Variables of SCO2 Recompression Cycle	Values
Minimum cycle temperature, T5	32 °C
Minimum cycle pressure, pmin	7.38 MPa
Maximum cycle pressure, pmax	25 MPa
Effectiveness of the SCO2 LTR, εLTR	95%
Effectiveness of the SCO2 HTR, εHTR	95%
Efficiency of the SCO2 turbine, ηT	93%
Efficiency of the SCO2 compressor, ηMC, ηRC	89%
SCO2 split ratio, SR	optimized

and other simulation settings are left unchanged from those of Turchi et al. [47]. As seen in Figure 3, the discrepancies between the present thermal efficiency data and Turchi et al.’s data [47] are all in the range of −1.81 to 0.15 percentages, with a small standard deviation of only 0.486 percentages for the absolute values of these discrepancies. Due to the good consistency between the present results and those of Turchi et al. [47], the present model can be considered trustworthy.

2.2. Cycle Performance Indexes

The thermodynamic performance of the two SCO₂ cycles for the next-generation SPT plant can be evaluated by considering three parameters as essential performance indexes.

Firstly, it is important to acknowledge that a larger heat storage temperature difference (ΔT) between the two heat storage tanks can significantly improve each cycle’s compatibility with the heat storage unit, thus playing a crucial role in the plant’s efficient operation [48,49]. Therefore, ΔT is selected as a critical performance index, as expressed in Equation (9).

$$\Delta T=T_{\mathrm{A}}-T_{\mathrm{B}}$$

(9)

Here, T_A is the HTF temperature in the hot tank or at the heater inlet/°C; T_B is the HTF temperature in the cold tank or at the heater outlet/°C.

Secondly, the specific work (w) and thermal efficiency (η_th) of an SCO₂ Brayton cycle are crucial factors in reducing the sizes of the cycle equipment and the heliostat field, respectively. η_th is defined as the ratio between the net power produced by the cycle (W_net) and the heat power absorbed by the cycle (Q). w represents the output power that can be generated by one kilogram working fluid. Therefore, improving these parameters can contribute to lowering the overall capital cost of the cycle.

2.3. Optimization Approach

The Non-dominated Sorting Genetic Algorithm II (NSGA-II) is a multi-objective optimization algorithm developed by Kalyanmoy Deb in 2002 [50].

NSGA-II operates through iterative improvements of a population of individuals across multiple generations. Each generation begins with non-dominated sorting being performed by NSGA-II to partition the individuals into different fronts based on their non-dominance levels. Subsequently, NSGA-II assigns a fitness value to each individual, taking into account both their front assignment and crowding distance. To generate new offspring solutions from the existing population, NSGA-II employs genetic operators such as crossovers and mutations. These offspring solutions are then evaluated and added to the population considering their non-dominances and crowding distances. This iterative process continues for multiple generations until NSGA-II converges to a set of solutions that are non-dominated, representing an optimal trade-off among conflicting objectives.

Due to its proven capability to optimize several conflicting objectives simultaneously, NSGA-II has been widely used in solving various real-world optimization problems [51,52]. In the current optimization, NSGA-II has also been chosen to optimize the SCO₂ cycles for next-generation SPT plants. The variables selected for optimization are the operating pressures (p_max, p_min), SCO₂ split ratio (SR), and effectiveness of the regenerators (ε_R, ε_HTR, ε_LTR). The optimization ranges for these variables are provided in

Table 4. Variable optimization ranges settings.

Variable	pmax	pmin	εR	εHTR	εLTR	SR
Range	15~30 MPa	7.4~10 MPa	0.75~0.95	0.75~0.95	0.75~0.95	0.3~1

. The optimization objectives include the specific work (w), the heat storage temperature difference (ΔT), and the thermal efficiency (η_th).

To begin the optimization process, a first-generation population of 200 individuals is created. Each individual’s phenotype represents the three optimization objectives. The genes in the i^th individual’s chromosome (X_i) determine its phenotypes and represent the variables to be optimized, which can be expressed using Equation (10).

$$X_i=\left\{\begin{array}{ll}\left(p_{\max },p_{\min },{\epsilon }_{\mathrm{R}}\right)& \mathrm{for} {\mathrm{SCO}}_2 \mathrm{regenerative} \mathrm{cycle}\\ \left(p_{\max },p_{\min },{\epsilon }_{\mathrm{HTR}},{\epsilon }_{\mathrm{LTR}},SR\right)& \mathrm{for} {\mathrm{SCO}}_2 \mathrm{recompression} \mathrm{cycle}\end{array}\right.$$

(10)

Here, i = 1, 2, …, 200.

The optimization process involves the utilization of genetic operators such as selection, crossover, and mutation, as well as techniques like fast non-dominant sorting, elite strategy, and crowding distance. These approaches are implemented to enhance the efficiency and effectiveness of the optimization process. Following 300 generations of evolution, the population converges into the final optimized population, where each individual exhibits optimized phenotypes including optimized ΔT_i, w_i, and η_th,i.

3. Results and Discussion

In this section, firstly, a variable analysis will be employed to investigate the impacts of operating pressure, regenerator effectiveness, and SCO₂ split ratio on thermal efficiency, specific work, and heat storage temperature difference. Subsequently, a triple-objective optimization for each SCO₂ cycle will be conducted, and the optimization results will be compared and discussed. Finally, the relationships between the optimized variables and the three optimization objectives will be further analyzed.

3.1. Variable Analysis

This section investigates the influences of key variables on the cycle performance of the relevant SCO₂ Brayton cycles. The variables of interest include the maximum and minimum pressures (p_max, p_min), SCO₂ split ratio (SR), and the effectiveness of all regenerators (ε_R, ε_HTR, ε_LTR). To fully comprehend the impacts of these variables on the cycle performance, it is imperative to examine the change in each performance index as each variable is raised. During the variable analysis, while one variable is being raised, the other variables maintain constant values, as indicated in

Table 5. Settings of input variables for variable analysis.

Variables	Settings
Maximum pressure, pmax	25 MPa
Minimum pressures, pmin	7.4 MPa
Regenerator effectiveness, εR	0.95
HTR effectiveness, εHTR	0.95
LTR effectiveness, εLTR	0.95
SCO2 split ratio, SR	0.7

. By comprehensively analyzing the influences of each variable, a deeper understanding of their individual contributions to the cycle performance can be attained.

3.1.1. Influences of the Maximum Cycle Pressure

Firstly, the impacts of the maximum pressure (p_max) on the specific work (w), heat storage temperature difference (ΔT) and thermal efficiency (η_th) of each of the two SCO₂ cycles are analyzed. The results are displayed in Figure 4, where p_max = 14~30 MPa.

With the rise of p_max, Figure 4 reveals, specific work (w) increases monotonically for both cycles. The reason for this is that the work output by the turbine and the work consumed by the compressor are both increased. However, since the work output increases more rapidly than the work consumed, the cycle net work (W_net) and the specific work (w) keep increasing. Secondly, ΔT also increases monotonically for both cycles as the SCO₂ temperatures at the regenerator’s hot terminal (t₂ and t₆ in Figure 1; t₂ and t₁₀ in Figure 2) decrease with a rising p_max. Furthermore, the change trend of the heat obtained by the SCO₂ from the heater (Q) is always consistent with that of the ΔT. Figure 4 illustrates that the regenerative cycle’s η_th rises with a rising p_max since the improvement in cycle net work (W_net) outpaces that of the heat obtained by the SCO₂ from the heater (Q) in the regenerative cycle, resulting in an increasing trend for η_th. However, the recompression cycle’s η_th initially rises, achieving its highest value of 52.61% when p_max reaches around 22 MPa, and then monotonously decreases. This is due to the fact that when p_max is within 14~22 MPa, the increment in cycle net work (W_net) outpaces that of the heat obtained by the SCO₂ from the heater (Q), while the situation reverses after p_max exceeds 22 MPa.

By comparing the performance of the two cycles in Figure 4, it can be found that the regenerative cycle generates larger specific work (w) and a wider heat storage temperature difference (ΔT) than the recompression cycle. Additionally, it achieves its maximum ΔT and w of 289.3 °C and 171.6 kW·kg⁻¹, respectively, at a p_max of 30 MPa. Meanwhile, the recompression cycle is able to generate a higher thermal efficiency (η_th).

3.1.2. Influences of the Minimum Cycle Pressure

The impacts of the minimum cycle pressure (p_min) on the specific work (w), the thermal efficiency (η_th), and the heat storage temperature difference (ΔT) performed by each of the two SCO₂ cycles are displayed in Figure 5, where p_min = 7.4~10 MPa.

Firstly, the rise in p_min results in increases in the specific work (w) for both cycles at the initial stage. When p_min reaches the pseudo-critical pressure of 8.2 MPa [53,54], the two cycles reach their maximum w values. For the recompression cycle, its maximum w is 146.3 kW·kg⁻¹, and the corresponding value is 159.9 kW·kg⁻¹ for the regenerative cycle. Moreover, when p_min exceeds 8.2 MPa, the w values of both cycles decrease monotonically.

Secondly, Figure 5 indicates that the two cycles’ ΔT values marginally improve as p_min rises from 7.4 MPa to 8.2 MPa and that these values attain their maxima (of 213.4 °C for the recompression cycle and 283.4 °C for the regenerative cycle) at 8.2 MPa. When p_min exceeds 8.2 MPa, the ΔT values of both cycles begin to monotonously decline. In general, an increase in p_min leads to a rise in the turbine outlet temperature (T₂ in Figure 1 and Figure 2) and an increase in the SCO₂ temperature at the outlet of the regenerator (T₆ in Figure 1 and T₁₀ in Figure 2), resulting in a monotonic decrease in ΔT. However, when p_min is below 8.2 MPa, the high-pressure SCO₂ temperature at the regenerator’s outlet decreases slightly with the rising p_min. Hence, it is not surprising that the ΔT values of both cycles increase slightly within this p_min range.

Lastly, as illustrated in Figure 5, an increase in p_min initially results in an improvement in the η_th of the recompression cycle. Subsequently, the η_th remains almost constant at its maximum value of 55.1% within the p_min range of 8 MPa to 9 MPa. When p_min exceeds 9 MPa, the η_th starts to decrease. In contrast, the η_th of the regenerative cycle first declines to its minimum value of 44.69% at the p_min of 9.2 MPa and then starts to rise slightly.

3.1.3. Influences of the Regenerator Effectiveness

The impacts of the effectiveness of the regenerators on the thermal efficiency (η_th), the specific work (w), and the heat storage temperature difference (ΔT) performed by the two SCO₂ cycles are displayed in Figure 6. To simplify the analysis, the effectiveness of the LTR and HTR in the recompression cycle (ε_LTR, ε_HTR) are always equal to the regenerator effectiveness (ε_R), and ε_R is in the range of 0.75~0.95.

Firstly, there is no doubt that the w of the regenerative cycle is not changed by an increasing ε_R. This is because changing ε_R will not affect the work output by the turbine and the work consumed by the compressor. However, the SCO₂ temperature at the re-compressor inlet (T_4b in Figure 2) is decreased with an increasing ε_R, resulting in a decrease in the re-compressor’s work consumption. Therefore, for the recompression cycle, its w increases slightly with an increasing ε_R.

Secondly, as depicted in Figure 6, the heat storage temperature differences (ΔT) of both cycles narrow with an increasing ε_R. This is because an increase in ε_R raises the high-pressure SCO₂ temperature at the regenerator outlet (T₆ in Figure 1 and t₁₀ in Figure 2), resulting in an increase in the temperature of the heat transfer fluid at the heater outlet (T_B). Moreover, the regenerative cycle exhibits a maximum ΔT of 352.3 °C when the ε_R value is 0.75.

Finally, the analysis reveals that the net work (W_net) values of both cycles remain almost unchanged while the amount of heat transferred to the SCO₂ from the heater (Q) gradually decreases. Consequently, the thermal efficiencies (η_th) of both cycles monotonously increase. Additionally, compared to the regenerative cycle, the recompression cycle demonstrates a higher η_th, with a maximum η_th of 52.42% achieved at an ε_R of 0.95.

3.1.4. Influences of the SCO₂ Split Ratio

The impacts of the split ratio (SR) of the SCO₂ on the heat storage temperature difference (ΔT), the thermal efficiency (η_th), and the specific work (w) of the SCO₂ recompression cycle are illustrated in Figure 7, where SR ranges from 0.3 to 1.0.

As demonstrated in Figure 7, an increase in SR yields improvements in both w and ΔT in the recompression cycle. This is due to the reduction in SCO₂ compressed by the re-compressor with an increasing SR, allowing the main compressor to compress more SCO₂ at a lower temperature. As a result, the compression work consumed by the recompression cycle is decreased, thereby increasing its net work (W_net) and w. Furthermore, a greater amount of SCO₂ flows back to the LTR with an increasing SR, decreasing the outlet temperatures of LTR and HTR (T₇ and T₁₀), ultimately reducing T_B. Simultaneously, an increase in SR first leads to an increase in η_th, which reaches its maximum value of 53.82% at SR = 0.75, and is then followed by a gradual decrease.

Based on the results presented in Figure 4, Figure 5 and Figure 6, it is evident that the regenerative cycle outperforms the recompression cycle in terms of specific work (w). This is due to the fact that the expansion processes of the two SCO₂ cycles produce comparable power (W_T). In the simple regenerative cycle, all SCO₂ enters the main compressor and is compressed at the lowest temperature. In contrast, a portion of SCO₂ in the recompression cycle (state 4b in Figure 2) is compressed at a higher temperature by the re-compressor (RC), requiring additional compression work. Consequently, the recompression cycle consumes more compression work, resulting in lower W_net and w. Nonetheless, the recompression cycle improves the temperature of high-pressure SCO₂ at the outlet of each regenerator by splitting SCO₂, thereby achieving lower ΔT and Q. Although the Q and the W_net of the recompression cycle are lower than those of the regenerative cycle, the effect of Q reduction is greater, resulting in higher η_th than in the regenerative cycle.

3.2. Results of the Triple-Objective Optimization

The preceding analysis of variables demonstrates the intricate effects of the operating pressures (p_max, p_min) of the SCO₂ Brayton cycle, the SCO₂ split ratio (SR), and the effectiveness of all regenerators (ε_R, ε_HTR, ε_LTR) on the specific work (w), the heat storage temperature difference (ΔT), and the thermal efficiency (η_th) of each of the two SCO₂ cycles. On one hand, when any of these variables change, the resulting trends in the three performance indicators vary. On the other hand, the trends of individual performance indicators are not always monotonic. In other words, a specific combination of these variables cannot maximize all performance indicators simultaneously. To reach a compromise among the different performance indicators, a triple-objective optimization approach is employed.

3.2.1. Pareto Solutions for the Two SCO₂ Brayton Cycles

Triple-objective optimization is performed for the two SCO₂ cycles in accordance with the optimization approach described in Section 2.3. The essential operational variables are outlined in Table 1, while the variables subject to optimization are provided in Table 4. During the optimization of each cycle, each cycle underwent three optimization runs, resulting in three Pareto solutions. The Pareto solution that demonstrated the highest overall performance was chosen to represent the optimization outcomes for each cycle. Figure 8 illustrates the final Pareto solutions for the two cycles in a spatial coordinate system consisting of “η_th, ΔT and w”. To facilitate a comparison between the two cycles, their Pareto solutions were plotted on separate plane coordinate systems, which have been presented in Figure 9 and Figure 10.

Figure 9 depicts the mapping of all points in Figure 8 onto the “w and η_th” coordinate system. The results reveal that the recompression cycle cannot improve both w and η_th simultaneously. Specifically, a decrease in η_th cannot always lead to a larger w, and when w is lower than 180 kW·kg⁻¹, an improvement in w will result in a deterioration in η_th. At point A, the recompression cycle achieves its maximum η_th of 55.95%, which is 8.76% higher than the maximum η_th of the regenerative cycle. Additionally, for the regenerative cycle, an increase in η_th does not affect its w within the range of the entire optimization results, and its w values are consistently higher than those of the recompression cycle. At point B, the two optimization objectives of the regenerative cycle are maximized simultaneously (η_th = 47.19%, w = 180.6 kW·kg⁻¹).

Figure 10 illustrates the mapping of all points in Figure 8 onto the “ΔT and η_th” coordinate system. The results reveal that the η_th values of the two cycles exhibit a conflicting relationship with their ΔT values and that both objectives cannot be maximized concurrently. Specifically, the optimized recompression cycle achieves higher η_th, while the regenerative cycle obtains higher ΔT. By dividing Figure 10 into three areas, a detailed analysis of the results can be conducted. In area I, only the recompression cycle can achieve an η_th higher than 47.19% and a ΔT narrower than 305.4 °C, it and achieves the maximum η_th value of 55.95% and the minimum ΔT value of 232.2 °C at point A. In area II, where η_th is between 43.92% and 47.19%, the optimized ΔT values for both cycles are between 305.4 °C and 327.3 °C, and the two cycles exhibit similar optimization performance. In area III, only the regenerative cycle can provide a ΔT wider than 327.3 °C and an η_th lower than 43.92% and reach the maximum ΔT value of 396.4 °C and the minimum η_th value of 36.34% at point C.

3.2.2. Optimizing the Relations between Variables and Objectives

To further analyze the relationships between the optimized variables and the three optimization objectives (η_th, w, and ΔT) of each cycle, Figure 11, Figure 12, Figure 13 and Figure 14 display the distributions of the six optimized variables relating to the Pareto solution of each cycle.

Figure 11 shows the distributions of the optimized cycle pressures (p_max and p_min) corresponding to the Pareto solutions. It is obvious from Figure 11a,b that the optimized p_max values of the regenerative cycle and the recompression cycle are fixed at around 29.96 MPa and 29.9 MPa, respectively, while their optimized p_min values are fixed at 8.20 MPa and 8.23 MPa, respectively. Therefore, the p_max and the p_min of each cycle should be close to these fixed values regardless of any requirements for the cycle’s performance.

Figure 12 shows the distributions of the optimized regenerator effectiveness (ε_HTR and ε_LTR) corresponding to the recompression cycle’s Pareto solution. Figure 12a,b show that the influence of the varying optimized ε_HTR on each optimization objective is similar to that of the varying optimized ε_LTR, and their distributions both cover the entire optimization range.

Firstly, when the optimized ε_HTR and ε_LTR are lower than the upper bounds of their optimization ranges (0.95), the w of the recompression cycle remains at its maximum value of about 180 kW·kg⁻¹, and the η_th generally increases with the optimized ε_HTR and ε_LTR while the ΔT has an opposite variation. Secondly, when the optimized ε_HTR and ε_LTR almost reach their upper bounds of 0.95, the three optimization objectives also change within a certain range. In this case, the η_th can be increased from 50.55% to its maximum value of 55.95%, and the ΔT and the w can be decreased from 284.4 °C and 180 kW·kg⁻¹ to their minimum values of 232.2 °C and 163.1 kW·kg⁻¹, respectively. Therefore, under the optimized operating condition, the ε_HTR and the ε_LTR of the recompression cycle should reach their upper bounds of 0.95 when the η_th is required to be as high as possible, which may also lead to the reduction of the w. On the contrary, the ε_HTR and ε_LTR should reach their lower bounds of 0.75 when the ΔT is required to be as high as possible.

Figure 13 displays the distribution of the optimized regenerator effectiveness (ε_R) corresponding to the regenerative cycle’s Pareto solution. Figure 13 demonstrates that the range of optimized ε_R and its influences on the three optimization objectives align with those observed for ε_HTR and ε_LTR in Figure 12. The notable distinction lies in the fact that the three optimization objectives remain unchanged when the optimized ɛ_R approaches its upper bound of 0.95.

Figure 14 depicts the distribution of the optimized SCO₂ split ratio (SR) corresponding to the recompression cycle’s Pareto solution. Figure 14 clearly demonstrates that the distribution of the optimized SR is concentrated in the range of 0.7–1.0, and the variation of the optimized SR within this range has a significant impact on the three optimization objectives. Firstly, when the optimized SR is lower than the upper bound of its optimization range, the η_th generally decreases with the increase of the optimized SR while the ΔT and the w have opposite variations. Secondly, when the optimized SR almost reaches its upper bound of 1.0, the w reaches its maximum value of 180 kW·kg⁻¹ and remains unchanged. Meanwhile, the η_th could be further decreased from 50.07% to its minimum value of 43.92%, and the ΔT could be further increased from 287.3 °C to its maximum value of 327.3 °C. It can be found that when SR reaches 1.0, the recompression cycle can produce almost the same maximum w as the regenerative cycle.

4. Conclusions

In this work, an optimization model combining a steady-state thermodynamic model and a multi-objective genetic algorithm has been developed for SCO₂ Brayton cycles. Compared with existing models, the present optimization model not only can predict the cycle performance reliably but also can optimize the cycle by considering three critical performance indexes, including the thermal efficiency, the specific work, and the heat storage temperature difference, as the objectives. Based on this model, the SCO₂ regenerative cycle and the SCO₂ recompression cycle for a next-generation SPT system have been studied and optimized, and the following conclusions can be obtained.

(1)

Variable analysis reveals that the minimum and maximum cycle pressures, the SCO₂ split ratio, and the effectiveness of the regenerators have complex influences on the three performance indexes—thermal efficiency (η_th), specific work (w), and heat storage temperature difference (ΔT). The variation trends of the three performance indexes are different and not always monotonous. A set of certain values of the above variables cannot make the three performance indexes reach their maximum values at the same time.

(2)

By comparing the two Pareto solutions obtained by the triple-objective optimization, the variation relationships among the three performance indexes are obtained. It is found that the η_th of the recompression cycle exhibits a conflicting relationship with its ΔT and w. Meanwhile, there is also a conflicting relationship between η_th and ΔT in the regenerative cycle, while the changes between η_th and w do not affect each other. For the three performance indexes, the recompression cycle can produce a higher optimal η_th, while the regenerative cycle can produce a wider optimal ΔT and larger optimal w. Meanwhile, the recompression cycle could obtain the highest η_th of 55.95%, while the widest ΔT and the largest w of 396.4 °C and 180.6 kW·kg⁻¹ can be obtained by the regenerative cycle, respectively.

(3)

When analyzing the distributions of the six optimized variables, it is found that the minimum and maximum cycle pressures in the two cycles have their fixed optimized values. Meanwhile, the solution of the regenerator effectiveness covers the entire optimization range, and the solution of the optimized SCO₂ split ratio is concentrated in the range of 0.7–1.0. Moreover, the largest optimal w generated by the two cycles is almost the same when the optimized SCO₂ split ratio is close to 1.0.

(4)

In realistic applications, different SCO₂ cycles and corresponding optimized variables could be considered when running the SCO₂ cycles with different specific performance demands. If the η_th is required to be as high as possible, the recompression cycle should be adopted, and its regenerator effectiveness should be increased, while the split ratio should be reduced. If the requirement for the ΔT or the w need to be considered as the key index, the regenerative cycle should be applied, and the optimized regenerator effectiveness should be reduced.

The developed model only can investigate the performance of SCO₂ cycles under steady state. Future work can focus on establishing a dynamic model that considers the whole SPT system including the heliostat field, the solar receiver, the thermal storage, and the SCO₂ cycle.